Computer Arithmetic
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Comparison of Parallel and Pipelined CORDIC Algorithm Using RCA and CSA
Comparison of Parallel and Pipelined CORDIC algorithm using RCA and CSA Diego Barragan´ Guerrero Lu´ıs Geraldo P. Meloni FEEC - UNICAMP FEEC - UNICAMP Campinas, Sao˜ Paulo, Brazil, 13083-852 Campinas, Sao˜ Paulo, Brazil, 13083-852 +5519 9308-9952 +5519 9778-1523 [email protected] [email protected] Abstract— This paper presents an implementation of the algorithm has two modes of operation: the rotational mode CORDIC algorithm in digital hardware using two types of (RM) where the vector (xi; yi) is rotated by an angle θ to algebraic adders: Ripple-Carry Adder (RCA) and Carry-Select obtain a new vector (x ; y ), and the vectoring mode (VM) Adder (CSA), both in parallel and pipelined architectures. Anal- N N ysis of time performance and resources utilization was carried in which the algorithm computes the modulus R and phase α out by changing the algorithm number of iterations. These results from the x-axis of the vector (x0; y0). The basic principle of demonstrate the efficiency in operating frequency of the pipelined the algorithm is shown in Figure 1. architecture with respect to the parallel architecture. Also it is shown that the use of CSA reduce the timing processing without significantly increasing the slice use. The code was synthesized us- ing FPGA development tools for the Xilinx Spartan-3E xc3s500e ' ' E N y family. N E N Index Terms— CORDIC, pipelined, parallel, RCA, CSA, y N trigonometrics functions. Rotação Pseudo-rotação R N I. INTRODUCTION E i In Digital Signal Processing with FPGA, trigonometric y i R i functions are used in many signal algorithms, for instance N synchronization and equalization [12]. -

Basics of Logic Design Arithmetic Logic Unit (ALU) Today's Lecture
Basics of Logic Design Arithmetic Logic Unit (ALU) CPS 104 Lecture 9 Today’s Lecture • Homework #3 Assigned Due March 3 • Project Groups assigned & posted to blackboard. • Project Specification is on Web Due April 19 • Building the building blocks… Outline • Review • Digital building blocks • An Arithmetic Logic Unit (ALU) Reading Appendix B, Chapter 3 © Alvin R. Lebeck CPS 104 2 Review: Digital Design • Logic Design, Switching Circuits, Digital Logic Recall: Everything is built from transistors • A transistor is a switch • It is either on or off • On or off can represent True or False Given a bunch of bits (0 or 1)… • Is this instruction a lw or a beq? • What register do I read? • How do I add two numbers? • Need a method to reason about complex expressions © Alvin R. Lebeck CPS 104 3 Review: Boolean Functions • Boolean functions have arguments that take two values ({T,F} or {0,1}) and they return a single or a set of ({T,F} or {0,1}) value(s). • Boolean functions can always be represented by a table called a “Truth Table” • Example: F: {0,1}3 -> {0,1}2 a b c f1f2 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 © Alvin R. Lebeck CPS 104 4 Review: Boolean Functions and Expressions F(A, B, C) = (A * B) + (~A * C) ABCF 0000 0011 0100 0111 1000 1010 1101 1111 © Alvin R. Lebeck CPS 104 5 Review: Boolean Gates • Gates are electronics devices that implement simple Boolean functions Examples a a AND(a,b) OR(a,b) a NOT(a) b b a XOR(a,b) a NAND(a,b) b b a NOR(a,b) a XNOR(a,b) b b © Alvin R. -

On the Hardware Reduction of Z-Datapath of Vectoring CORDIC
On the Hardware Reduction of z-Datapath of Vectoring CORDIC R. Stapenhurst*, K. Maharatna**, J. Mathew*, J.L.Nunez-Yanez* and D. K. Pradhan* *University of Bristol, Bristol, UK **University of Southampton, Southampton, UK [email protected] Abstract— In this article we present a novel design of a hardware wordlength larger than 18-bits the hardware requirement of it optimal vectoring CORDIC processor. We present a mathematical becomes more than the classical CORDIC. theory to show that using bipolar binary notation it is possible to eliminate all the arithmetic computations required along the z- In this particular work we propose a formulation to eliminate datapath. Using this technique it is possible to achieve three and 1.5 all the arithmetic operations along the z-datapath for conventional times reduction in the number of registers and adder respectively two-sided vector rotation and thereby reducing the hardware compared to classical CORDIC. Following this, a 16-bit vectoring while increasing the accuracy. Also the resulting architecture CORDIC is designed for the application in Synchronizer for IEEE shows significant hardware saving as the wordlength increases. 802.11a standard. The total area and dynamic power consumption Although we stick to the 2’s complement number system, without of the processor is 0.14 mm2 and 700μW respectively when loss of generality, this formulation can be adopted easily for synthesized in 0.18μm CMOS library which shows its effectiveness redundant arithmetic and higher radix formulation. A 16-bit as a low-area low-power processor. processor developed following this formulation requires 0.14 mm2 area and consumes 700 μW dynamic power when synthesized in 0.18μm CMOS library. -

18-447 Computer Architecture Lecture 6: Multi-Cycle and Microprogrammed Microarchitectures
18-447 Computer Architecture Lecture 6: Multi-Cycle and Microprogrammed Microarchitectures Prof. Onur Mutlu Carnegie Mellon University Spring 2015, 1/28/2015 Agenda for Today & Next Few Lectures n Single-cycle Microarchitectures n Multi-cycle and Microprogrammed Microarchitectures n Pipelining n Issues in Pipelining: Control & Data Dependence Handling, State Maintenance and Recovery, … n Out-of-Order Execution n Issues in OoO Execution: Load-Store Handling, … 2 Reminder on Assignments n Lab 2 due next Friday (Feb 6) q Start early! n HW 1 due today n HW 2 out n Remember that all is for your benefit q Homeworks, especially so q All assignments can take time, but the goal is for you to learn very well 3 Lab 1 Grades 25 20 15 10 5 Number of Students 0 30 40 50 60 70 80 90 100 n Mean: 88.0 n Median: 96.0 n Standard Deviation: 16.9 4 Extra Credit for Lab Assignment 2 n Complete your normal (single-cycle) implementation first, and get it checked off in lab. n Then, implement the MIPS core using a microcoded approach similar to what we will discuss in class. n We are not specifying any particular details of the microcode format or the microarchitecture; you can be creative. n For the extra credit, the microcoded implementation should execute the same programs that your ordinary implementation does, and you should demo it by the normal lab deadline. n You will get maximum 4% of course grade n Document what you have done and demonstrate well 5 Readings for Today n P&P, Revised Appendix C q Microarchitecture of the LC-3b q Appendix A (LC-3b ISA) will be useful in following this n P&H, Appendix D q Mapping Control to Hardware n Optional q Maurice Wilkes, “The Best Way to Design an Automatic Calculating Machine,” Manchester Univ. -

Implementation of Carry Tree Adders and Compare with RCA and CSLA
International Journal of Emerging Engineering Research and Technology Volume 4, Issue 1, January 2016, PP 1-11 ISSN 2349-4395 (Print) & ISSN 2349-4409 (Online) Implementation of Carry Tree Adders and Compare with RCA and CSLA 1 2 G. Venkatanaga Kumar , C.H Pushpalatha Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (PG Scholar) Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (Associate Professor) ABSTRACT The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Binary adders are one of the most essential logic elements within a digital system. In addition, binary adders are also helpful in units other than Arithmetic Logic Units (ALU), such as multipliers, dividers and memory addressing. Therefore, binary addition is essential that any improvement in binary addition can result in a performance boost for any computing system and, hence, help improve the performance of the entire system. Parallel-prefix adders (also known as carry-tree adders) are known to have the best performance in VLSI designs. This paper investigates three types of carry-tree adders (the Kogge- Stone, sparse Kogge-Stone, Ladner-Fischer and spanning tree adder) and compares them to the simple Ripple Carry Adder (RCA) and Carry Skip Adder (CSA). In this project Xilinx-ISE tool is used for simulation, logical verification, and further synthesizing. This algorithm is implemented in Xilinx 13.2 version and verified using Spartan 3e kit. -
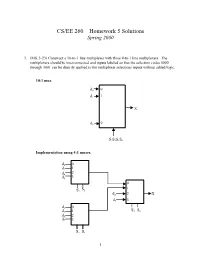
CS/EE 260 – Homework 5 Solutions Spring 2000
CS/EE 260 – Homework 5 Solutions Spring 2000 1. (MK 3-23) Construct a 10-to-1 line multiplexer with three 4-to-1 line multiplexers. The multiplexers should be interconnected and inputs labeled so that the selection codes 0000 through 1001 can be directly applied to the multiplexer selections inputs without added logic. 10:1 mux d0 0 1 d1 1 X d9 9 S3S2S1S0 Implementation using 4:1 muxes. d0 0 d2 1 d4 2 d6 3 0 S 1 S2 1 d8 2 X d9 3 d 0 1 S S d3 1 3 0 d5 2 d7 3 S2 S1 1 2. (MK 3-27) Implement a binary full adder with a dual 4-to-1 line multiplexer and a single inverter. AB Ci S Co 00 0 0 0 C 0 00 1 1 i 0 01 0 1 0 C ´ C 01 1 0 i 1 i 10 0 1 0 10 1 0Ci´ 1 Ci 11 0 0 1 C 1 11 1 1 i 1 0 C 1 i 4:1 2 S 3 mux S1 S0 A B 0 0 1 4:1 Co 2 mux 1 3 S1S0 2 3. (MK 3-34) Design a combinational circuit that forms the 2-bit binary sum S1S0 of two 2-bit numbers A1A0 and B1B0 and has both input C0 and a carry output C2. Do not use half adders or full adders, but instead use a two-level circuit plus inverters for the input variables, as needed. Design the circuit by starting with the following equations for each of the two bits of the adder. -

UNIT 8B a Full Adder
UNIT 8B Computer Organization: Levels of Abstraction 15110 Principles of Computing, 1 Carnegie Mellon University - CORTINA A Full Adder C ABCin Cout S in 0 0 0 A 0 0 1 0 1 0 B 0 1 1 1 0 0 1 0 1 C S out 1 1 0 1 1 1 15110 Principles of Computing, 2 Carnegie Mellon University - CORTINA 1 A Full Adder C ABCin Cout S in 0 0 0 0 0 A 0 0 1 0 1 0 1 0 0 1 B 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 C S out 1 1 0 1 0 1 1 1 1 1 ⊕ ⊕ S = A B Cin ⊕ ∧ ∨ ∧ Cout = ((A B) C) (A B) 15110 Principles of Computing, 3 Carnegie Mellon University - CORTINA Full Adder (FA) AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 4 Carnegie Mellon University - CORTINA 2 Another Full Adder (FA) http://students.cs.tamu.edu/wanglei/csce350/handout/lab6.html AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 5 Carnegie Mellon University - CORTINA 8-bit Full Adder A7 B7 A2 B2 A1 B1 A0 B0 1-bit 1-bit 1-bit 1-bit ... Cout Full Full Full Full Cin Adder Adder Adder Adder S7 S2 S1 S0 AB 8 ⁄ ⁄ 8 C 8-bit C out FA in ⁄ 8 S 15110 Principles of Computing, 6 Carnegie Mellon University - CORTINA 3 Multiplexer (MUX) • A multiplexer chooses between a set of inputs. D1 D 2 MUX F D3 D ABF 4 0 0 D1 AB 0 1 D2 1 0 D3 1 1 D4 http://www.cise.ufl.edu/~mssz/CompOrg/CDAintro.html 15110 Principles of Computing, 7 Carnegie Mellon University - CORTINA Arithmetic Logic Unit (ALU) OP 1OP 0 Carry In & OP OP 0 OP 1 F 0 0 A ∧ B 0 1 A ∨ B 1 0 A 1 1 A + B http://cs-alb-pc3.massey.ac.nz/notes/59304/l4.html 15110 Principles of Computing, 8 Carnegie Mellon University - CORTINA 4 Flip Flop • A flip flop is a sequential circuit that is able to maintain (save) a state. -

Datapath Design I Systems I
Systems I Datapath Design I Topics Sequential instruction execution cycle Instruction mapping to hardware Instruction decoding Overview How do we build a digital computer? Hardware building blocks: digital logic primitives Instruction set architecture: what HW must implement Principled approach Hardware designed to implement one instruction at a time Plus connect to next instruction Decompose each instruction into a series of steps Expect that most steps will be common to many instructions Extend design from there Overlap execution of multiple instructions (pipelining) Later in this course Parallel execution of many instructions In more advanced computer architecture course 2 Y86 Instruction Set Byte 0 1 2 3 4 5 nop 0 0 addl 6 0 halt 1 0 subl 6 1 rrmovl rA, rB 2 0 rA rB andl 6 2 irmovl V, rB 3 0 8 rB V xorl 6 3 rmmovl rA, D(rB) 4 0 rA rB D jmp 7 0 mrmovl D(rB), rA 5 0 rA rB D jle 7 1 OPl rA, rB 6 fn rA rB jl 7 2 jXX Dest 7 fn Dest je 7 3 call Dest 8 0 Dest jne 7 4 ret 9 0 jge 7 5 pushl rA A 0 rA 8 jg 7 6 popl rA B 0 rA 8 3 Building Blocks fun Combinational Logic A A = Compute Boolean functions of L U inputs B 0 Continuously respond to input changes MUX Operate on data and implement 1 control Storage Elements valA A srcA Store bits valW Register W file dstW Addressable memories valB B Non-addressable registers srcB Clock Loaded only as clock rises Clock 4 Hardware Control Language Very simple hardware description language Can only express limited aspects of hardware operation Parts we want to explore and modify Data -

Design of High Speed and Low Power Six Transistor Full Adder Using Two Transistor Xor Gate
International Journal of Electronics, Communication & Instrumentation Engineering Research and Development (IJECIERD) ISSN 2249-684X Vol. 3, Issue 1, Mar 2013, 87-96 © TJPRC Pvt. Ltd. DESIGN OF HIGH SPEED AND LOW POWER SIX TRANSISTOR FULL ADDER USING TWO TRANSISTOR XOR GATE B. DILLI KUMAR, K. CHARAN KUMAR & T. NAVEEN KUMAR M. Tech (VLSI), Department of ECE, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, India ABSTRACT Full adder is one of the major components in the design of many sophisticated hardware circuits. In this paper the full adder has been designed by using a new efficient design with less number of transistors. A 2 transistor XOR gate has been proposed with the help of two PMOS (Positive Metal Oxide Semiconductor) transistors. By using this 2T XOR gate the size of the full adder has been decreased to a large extent which can be implemented with only 6 transistors. The proposed full adder has a significant improvement in silicon area and power delay product when compared to the previous 8T full adder circuits. Further the proposed adder requires less area to perform a required logic function. Further, the proposed full adder has less power dissipation which makes it suitable for many of the low power applications and because of less area requirement the proposed design can be used in many of the portable applications also . KEYWORDS: Full Adder, XOR, Less Area, Speed, Low Power, Delay, Less Transistor Count, Low Power VLSI INTRODUCTION Full adder is one of the basic building blocks of many of the digital VLSI circuits. Several refinements has been made regarding its structure since its invention. -

LECTURE 5 Single-Cycle Datapath and Control
Single-Cycle LECTURE 5 Datapath and Control PROCESSORS In lecture 1, we reminded ourselves that the datapath and control are the two components that come together to be collectively known as the processor. • Datapath consists of the functional units of the processor. • Elements that hold data. • Program counter, register file, instruction memory, etc. • Elements that operate on data. • ALU, adders, etc. • Buses for transferring data between elements. • Control commands the datapath regarding when and how to route and operate on data. MIPS To showcase the process of creating a datapath and designing a control, we will be using a subset of the MIPS instruction set. Our available instructions include: • add, sub, and, or, slt • lw, sw • beq, j DATAPATH To start, we will look at the datapath elements needed by every instruction. First, we have instruction memory. Instruction memory is a state element that provides read-access to the instructions of a program and, given an address as input, supplies the corresponding instruction at that address. Code can also be written, e.g., self-modifying code DATAPATH Next, we have the program counter or PC. The PC is a state element that holds the address of the current instruction. Essentially, it is just a 32-bit register which holds the instruction address and is updated at the end of every clock cycle. Normally PC increments sequentially except for branch instructions The arrows on either side indicate that the PC state element is both readable and writeable. DATAPATH Lastly, we have the adder. The adder is responsible for incrementing the PC to hold the address of the next instruction. -

Effectiveness of the MAX-2 Multimedia Extensions for PA-RISC 2.0 Processors
Effectiveness of the MAX-2 Multimedia Extensions for PA-RISC 2.0 Processors Ruby Lee Hewlett-Packard Company HotChips IX Stanford, CA, August 24-26,1997 Outline Introduction PA-RISC MAX-2 features and examples Mix Permute Multiply with Shift&Add Conditionals with Saturation Arith (e.g., Absolute Values) Performance Comparison with / without MAX-2 General-Purpose Workloads will include Increasing Amounts of Media Processing MM a b a b 2 1 2 1 b c b c functionality 5 2 5 2 A B C D 1 2 22 2 2 33 3 4 55 59 A B C D 1 2 A B C D 22 1 2 22 2 2 2 2 33 33 3 4 55 59 3 4 55 59 Distributed Multimedia Real-time Information Access Communications Tool Tool Computation Tool time 1980 1990 2000 Multimedia Extensions for General-Purpose Processors MAX-1 for HP PA-RISC (product Jan '94) VIS for Sun Sparc (H2 '95) MAX-2 for HP PA-RISC (product Mar '96) MMX for Intel x86 (chips Jan '97) MDMX for SGI MIPS-V (tbd) MVI for DEC Alpha (tbd) Ideally, different media streams map onto both the integer and floating-point datapaths of microprocessors images GR: GR: 32x32 video 32x64 ALU SMU FP: graphics FP:16x64 Mem 32x64 audio FMAC PA-RISC 2.0 Processor Datapath Subword Parallelism in a General-Purpose Processor with Multimedia Extensions General Regs. y5 y6 y7 y8 x5 x6 x7 x8 x1 x2 x3 x4 y1 y2 y3 y4 Partitionable Partitionable 64-bit ALU 64-bit ALU 8 ops / cycle Subword Parallel MAX-2 Instructions in PA-RISC 2.0 Parallel Add (modulo or saturation) Parallel Subtract (modulo or saturation) Parallel Shift Right (1,2 or 3 bits) and Add Parallel Shift Left (1,2 or 3 bits) and Add Parallel Average Parallel Shift Right (n bits) Parallel Shift Left (n bits) Mix Permute MAX-2 Leverages Existing Processing Resources FP: INTEGER FLOAT GR: 16x64 General Regs. -

Half Adder, Which Finds the Sum of Two Bits
CMSC 313 COMPUTER ORGANIZATION & ASSEMBLY LANGUAGE PROGRAMMING LECTURE 21, SPRING 2013 TOPICS TODAY • Circuits for Addition • Standard Logic Components • Logisim Demo CIRCUITS FOR ADDITION 3.5 Combinational Circuits • Combinational logic circuits give us many useful devices. • One of the simplest is the half adder, which finds the sum of two bits. • We can gain some insight as to the construction of a half adder by looking at its truth table, shown at the right. 30 Half Adder • Inputs: A and B • Outputs: S = lower bit of A + B, cout = carry bit A B S cout 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 • Using Sum-of-Products: S = AB + AB, cout = AB. • Alternatively, we could use XOR: S = A ⊕ B. ! ! ! ! 1 3.5 Combinational Circuits • As we see, the sum can be found using the XOR operation and the carry using the AND operation. 31 3.5 Combinational Circuits • We can change our half adder into to a full adder by including gates for processing the carry bit. • The truth table for a full adder is shown at the right. 32 Full Adder • Inputs: A, B and cin • Outputs: S = lower bit of A + B, cout = carry bit A B cin S cout 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 • S = A BC + ABC + AB C + ABC = A ⊕ B ⊕ C.