DOCSLIB.ORG

UNIT 8B a Full Adder

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
UNIT 8B a Full Adder UNIT 8B Computer Organization: Levels of Abstraction 15110 Principles of Computing, 1 Carnegie Mellon University - CORTINA A Full Adder C ABCin Cout S in 0 0 0 A 0 0 1 0 1 0 B 0 1 1 1 0 0 1 0 1 C S out 1 1 0 1 1 1 15110 Principles of Computing, 2 Carnegie Mellon University - CORTINA 1 A Full Adder C ABCin Cout S in 0 0 0 0 0 A 0 0 1 0 1 0 1 0 0 1 B 0 1 1 1 0 1 0 0 0 1 1 0 1 1 0 C S out 1 1 0 1 0 1 1 1 1 1 ⊕ ⊕ S = A B Cin ⊕ ∧ ∨ ∧ Cout = ((A B) C) (A B) 15110 Principles of Computing, 3 Carnegie Mellon University - CORTINA Full Adder (FA) AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 4 Carnegie Mellon University - CORTINA 2 Another Full Adder (FA) http://students.cs.tamu.edu/wanglei/csce350/handout/lab6.html AB 1-bit Cout Full Cin Adder S 15110 Principles of Computing, 5 Carnegie Mellon University - CORTINA 8-bit Full Adder A7 B7 A2 B2 A1 B1 A0 B0 1-bit 1-bit 1-bit 1-bit ... Cout Full Full Full Full Cin Adder Adder Adder Adder S7 S2 S1 S0 AB 8 ⁄ ⁄ 8 C 8-bit C out FA in ⁄ 8 S 15110 Principles of Computing, 6 Carnegie Mellon University - CORTINA 3 Multiplexer (MUX) • A multiplexer chooses between a set of inputs. D1 D 2 MUX F D3 D ABF 4 0 0 D1 AB 0 1 D2 1 0 D3 1 1 D4 http://www.cise.ufl.edu/~mssz/CompOrg/CDAintro.html 15110 Principles of Computing, 7 Carnegie Mellon University - CORTINA Arithmetic Logic Unit (ALU) OP 1OP 0 Carry In & OP OP 0 OP 1 F 0 0 A ∧ B 0 1 A ∨ B 1 0 A 1 1 A + B http://cs-alb-pc3.massey.ac.nz/notes/59304/l4.html 15110 Principles of Computing, 8 Carnegie Mellon University - CORTINA 4 Flip Flop • A flip flop is a sequential circuit that is able to maintain (save) a state. – Example: D (Data) Flip-Flop – sets output Q to input D when clock turns on. (Images from Wikipedia) Clock Clock S=Set Q to 1, R=Reset Q to 0 15110 Principles of Computing, 9 Carnegie Mellon University - CORTINA Registers • A register is just a set of edge- triggered flip-flops. Registers are triggered by a clock signal. D 0 Q0 D1 Reg. Q1 D2 Q D 2 3 Q3 Clock http://cpuville.com/register.htm Clock 15110 Principles of Computing, 10 Carnegie Mellon University - CORTINA 5 Central Processing Unit (CPU) • A CPU contains: – Arithmetic Logic Unit to perform computation – Registers to hold information • Instruction register (current instruction being executed) • Program counter (to hold location of next instruction in memory) • Accumulator (to hold computation result from ALU) • Data register(s) (to hold other important data for future use) – Control unit to regulate flow of information and operations that are performed at each instruction step 15110 Principles of Computing, 11 Carnegie Mellon University - CORTINA A sample CPU http://cpuville.com/main.htm 15110 Principles of Computing, 12 Carnegie Mellon University - CORTINA 6 Computer http://cse.iitkgp.ac.in/pds/notes/intro.html 15110 Principles of Computing, 13 Carnegie Mellon University - CORTINA Abstraction • We can use layers of abstraction to hide details of the computer design. • We can work in any layer, not needing to know how the lower layers work or how the current layer fits into the larger system. -> transistors -> gates -> circuits (adders, multiplexors, flip-flops) -> central processing units (ALU, registers, control) -> computer 15110 Principles of Computing, 14 Carnegie Mellon University - CORTINA 7.
Load more

Recommended publications
  • Comparison of Parallel and Pipelined CORDIC Algorithm Using RCA and CSA
    Comparison of Parallel and Pipelined CORDIC algorithm using RCA and CSA Diego Barragan´ Guerrero Lu´ıs Geraldo P. Meloni FEEC - UNICAMP FEEC - UNICAMP Campinas, Sao˜ Paulo, Brazil, 13083-852 Campinas, Sao˜ Paulo, Brazil, 13083-852 +5519 9308-9952 +5519 9778-1523 [email protected] [email protected] Abstract— This paper presents an implementation of the algorithm has two modes of operation: the rotational mode CORDIC algorithm in digital hardware using two types of (RM) where the vector (xi; yi) is rotated by an angle θ to algebraic adders: Ripple-Carry Adder (RCA) and Carry-Select obtain a new vector (x ; y ), and the vectoring mode (VM) Adder (CSA), both in parallel and pipelined architectures. Anal- N N ysis of time performance and resources utilization was carried in which the algorithm computes the modulus R and phase α out by changing the algorithm number of iterations. These results from the x-axis of the vector (x0; y0). The basic principle of demonstrate the efficiency in operating frequency of the pipelined the algorithm is shown in Figure 1. architecture with respect to the parallel architecture. Also it is shown that the use of CSA reduce the timing processing without significantly increasing the slice use. The code was synthesized us- ing FPGA development tools for the Xilinx Spartan-3E xc3s500e ' ' E N y family. N E N Index Terms— CORDIC, pipelined, parallel, RCA, CSA, y N trigonometrics functions. Rotação Pseudo-rotação R N I. INTRODUCTION E i In Digital Signal Processing with FPGA, trigonometric y i R i functions are used in many signal algorithms, for instance N synchronization and equalization [12].
    [Show full text]
  • Basics of Logic Design Arithmetic Logic Unit (ALU) Today's Lecture
    Basics of Logic Design Arithmetic Logic Unit (ALU) CPS 104 Lecture 9 Today’s Lecture • Homework #3 Assigned Due March 3 • Project Groups assigned & posted to blackboard. • Project Specification is on Web Due April 19 • Building the building blocks… Outline • Review • Digital building blocks • An Arithmetic Logic Unit (ALU) Reading Appendix B, Chapter 3 © Alvin R. Lebeck CPS 104 2 Review: Digital Design • Logic Design, Switching Circuits, Digital Logic Recall: Everything is built from transistors • A transistor is a switch • It is either on or off • On or off can represent True or False Given a bunch of bits (0 or 1)… • Is this instruction a lw or a beq? • What register do I read? • How do I add two numbers? • Need a method to reason about complex expressions © Alvin R. Lebeck CPS 104 3 Review: Boolean Functions • Boolean functions have arguments that take two values ({T,F} or {0,1}) and they return a single or a set of ({T,F} or {0,1}) value(s). • Boolean functions can always be represented by a table called a “Truth Table” • Example: F: {0,1}3 -> {0,1}2 a b c f1f2 0 0 0 0 1 0 0 1 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 1 © Alvin R. Lebeck CPS 104 4 Review: Boolean Functions and Expressions F(A, B, C) = (A * B) + (~A * C) ABCF 0000 0011 0100 0111 1000 1010 1101 1111 © Alvin R. Lebeck CPS 104 5 Review: Boolean Gates • Gates are electronics devices that implement simple Boolean functions Examples a a AND(a,b) OR(a,b) a NOT(a) b b a XOR(a,b) a NAND(a,b) b b a NOR(a,b) a XNOR(a,b) b b © Alvin R.
    [Show full text]
  • Implementation of Carry Tree Adders and Compare with RCA and CSLA
    International Journal of Emerging Engineering Research and Technology Volume 4, Issue 1, January 2016, PP 1-11 ISSN 2349-4395 (Print) & ISSN 2349-4409 (Online) Implementation of Carry Tree Adders and Compare with RCA and CSLA 1 2 G. Venkatanaga Kumar , C.H Pushpalatha Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (PG Scholar) Department of ECE, GONNA INSTITUTE OF TECHNOLOGY, Vishakhapatnam, India (Associate Professor) ABSTRACT The binary adder is the critical element in most digital circuit designs including digital signal processors (DSP) and microprocessor data path units. As such, extensive research continues to be focused on improving the power delay performance of the adder. In VLSI implementations, parallel-prefix adders are known to have the best performance. Binary adders are one of the most essential logic elements within a digital system. In addition, binary adders are also helpful in units other than Arithmetic Logic Units (ALU), such as multipliers, dividers and memory addressing. Therefore, binary addition is essential that any improvement in binary addition can result in a performance boost for any computing system and, hence, help improve the performance of the entire system. Parallel-prefix adders (also known as carry-tree adders) are known to have the best performance in VLSI designs. This paper investigates three types of carry-tree adders (the Kogge- Stone, sparse Kogge-Stone, Ladner-Fischer and spanning tree adder) and compares them to the simple Ripple Carry Adder (RCA) and Carry Skip Adder (CSA). In this project Xilinx-ISE tool is used for simulation, logical verification, and further synthesizing. This algorithm is implemented in Xilinx 13.2 version and verified using Spartan 3e kit.
    [Show full text]
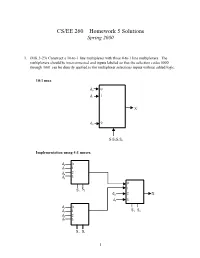
  • CS/EE 260 – Homework 5 Solutions Spring 2000
    CS/EE 260 – Homework 5 Solutions Spring 2000 1. (MK 3-23) Construct a 10-to-1 line multiplexer with three 4-to-1 line multiplexers. The multiplexers should be interconnected and inputs labeled so that the selection codes 0000 through 1001 can be directly applied to the multiplexer selections inputs without added logic. 10:1 mux d0 0 1 d1 1 X d9 9 S3S2S1S0 Implementation using 4:1 muxes. d0 0 d2 1 d4 2 d6 3 0 S 1 S2 1 d8 2 X d9 3 d 0 1 S S d3 1 3 0 d5 2 d7 3 S2 S1 1 2. (MK 3-27) Implement a binary full adder with a dual 4-to-1 line multiplexer and a single inverter. AB Ci S Co 00 0 0 0 C 0 00 1 1 i 0 01 0 1 0 C ´ C 01 1 0 i 1 i 10 0 1 0 10 1 0Ci´ 1 Ci 11 0 0 1 C 1 11 1 1 i 1 0 C 1 i 4:1 2 S 3 mux S1 S0 A B 0 0 1 4:1 Co 2 mux 1 3 S1S0 2 3. (MK 3-34) Design a combinational circuit that forms the 2-bit binary sum S1S0 of two 2-bit numbers A1A0 and B1B0 and has both input C0 and a carry output C2. Do not use half adders or full adders, but instead use a two-level circuit plus inverters for the input variables, as needed. Design the circuit by starting with the following equations for each of the two bits of the adder.
    [Show full text]
  • Design of High Speed and Low Power Six Transistor Full Adder Using Two Transistor Xor Gate
    International Journal of Electronics, Communication & Instrumentation Engineering Research and Development (IJECIERD) ISSN 2249-684X Vol. 3, Issue 1, Mar 2013, 87-96 © TJPRC Pvt. Ltd. DESIGN OF HIGH SPEED AND LOW POWER SIX TRANSISTOR FULL ADDER USING TWO TRANSISTOR XOR GATE B. DILLI KUMAR, K. CHARAN KUMAR & T. NAVEEN KUMAR M. Tech (VLSI), Department of ECE, Sree Vidyanikethan Engineering College (Autonomous), Tirupati, India ABSTRACT Full adder is one of the major components in the design of many sophisticated hardware circuits. In this paper the full adder has been designed by using a new efficient design with less number of transistors. A 2 transistor XOR gate has been proposed with the help of two PMOS (Positive Metal Oxide Semiconductor) transistors. By using this 2T XOR gate the size of the full adder has been decreased to a large extent which can be implemented with only 6 transistors. The proposed full adder has a significant improvement in silicon area and power delay product when compared to the previous 8T full adder circuits. Further the proposed adder requires less area to perform a required logic function. Further, the proposed full adder has less power dissipation which makes it suitable for many of the low power applications and because of less area requirement the proposed design can be used in many of the portable applications also . KEYWORDS: Full Adder, XOR, Less Area, Speed, Low Power, Delay, Less Transistor Count, Low Power VLSI INTRODUCTION Full adder is one of the basic building blocks of many of the digital VLSI circuits. Several refinements has been made regarding its structure since its invention.
    [Show full text]
  • With Extreme Scale Computing the Rules Have Changed
    With Extreme Scale Computing the Rules Have Changed Jack Dongarra University of Tennessee Oak Ridge National Laboratory University of Manchester 11/17/15 1 • Overview of High Performance Computing • With Extreme Computing the “rules” for computing have changed 2 3 • Create systems that can apply exaflops of computing power to exabytes of data. • Keep the United States at the forefront of HPC capabilities. • Improve HPC application developer productivity • Make HPC readily available • Establish hardware technology for future HPC systems. 4 11E+09 Eflop/s 362 PFlop/s 100000000100 Pflop/s 10000000 10 Pflop/s 33.9 PFlop/s 1000000 1 Pflop/s SUM 100000100 Tflop/s 166 TFlop/s 1000010 Tflop /s N=1 1 Tflop1000/s 1.17 TFlop/s 100 Gflop/s100 My Laptop 70 Gflop/s N=500 10 59.7 GFlop/s 10 Gflop/s My iPhone 4 Gflop/s 1 1 Gflop/s 0.1 100 Mflop/s 400 MFlop/s 1994 1996 1998 2000 2002 2004 2006 2008 2010 2012 2014 2015 1 Eflop/s 1E+09 420 PFlop/s 100000000100 Pflop/s 10000000 10 Pflop/s 33.9 PFlop/s 1000000 1 Pflop/s SUM 100000100 Tflop/s 206 TFlop/s 1000010 Tflop /s N=1 1 Tflop1000/s 1.17 TFlop/s 100 Gflop/s100 My Laptop 70 Gflop/s N=500 10 59.7 GFlop/s 10 Gflop/s My iPhone 4 Gflop/s 1 1 Gflop/s 0.1 100 Mflop/s 400 MFlop/s 1994 1996 1998 2000 2002 2004 2006 2008 2010 2012 2014 2015 1E+10 1 Eflop/s 1E+09 100 Pflop/s 100000000 10 Pflop/s 10000000 1 Pflop/s 1000000 SUM 100 Tflop/s 100000 10 Tflop/s N=1 10000 1 Tflop/s 1000 100 Gflop/s N=500 100 10 Gflop/s 10 1 Gflop/s 1 100 Mflop/s 0.1 1996 2002 2020 2008 2014 1E+10 1 Eflop/s 1E+09 100 Pflop/s 100000000 10 Pflop/s 10000000 1 Pflop/s 1000000 SUM 100 Tflop/s 100000 10 Tflop/s N=1 10000 1 Tflop/s 1000 100 Gflop/s N=500 100 10 Gflop/s 10 1 Gflop/s 1 100 Mflop/s 0.1 1996 2002 2020 2008 2014 • Pflops (> 1015 Flop/s) computing fully established with 81 systems.
    [Show full text]
  • Theoretical Peak FLOPS Per Instruction Set on Modern Intel Cpus
    Theoretical Peak FLOPS per instruction set on modern Intel CPUs Romain Dolbeau Bull – Center for Excellence in Parallel Programming Email: [email protected] Abstract—It used to be that evaluating the theoretical and potentially multiple threads per core. Vector of peak performance of a CPU in FLOPS (floating point varying sizes. And more sophisticated instructions. operations per seconds) was merely a matter of multiplying Equation2 describes a more realistic view, that we the frequency by the number of floating-point instructions will explain in details in the rest of the paper, first per cycles. Today however, CPUs have features such as vectorization, fused multiply-add, hyper-threading or in general in sectionII and then for the specific “turbo” mode. In this paper, we look into this theoretical cases of Intel CPUs: first a simple one from the peak for recent full-featured Intel CPUs., taking into Nehalem/Westmere era in section III and then the account not only the simple absolute peak, but also the full complexity of the Haswell family in sectionIV. relevant instruction sets and encoding and the frequency A complement to this paper titled “Theoretical Peak scaling behavior of current Intel CPUs. FLOPS per instruction set on less conventional Revision 1.41, 2016/10/04 08:49:16 Index Terms—FLOPS hardware” [1] covers other computing devices. flop 9 I. INTRODUCTION > operation> High performance computing thrives on fast com- > > putations and high memory bandwidth. But before > operations => any code or even benchmark is run, the very first × micro − architecture instruction number to evaluate a system is the theoretical peak > > - how many floating-point operations the system > can theoretically execute in a given time.
    [Show full text]
  • Misleading Performance Reporting in the Supercomputing Field David H
    Misleading Performance Reporting in the Supercomputing Field David H. Bailey RNR Technical Report RNR-92-005 December 1, 1992 Ref: Scientific Programming, vol. 1., no. 2 (Winter 1992), pg. 141–151 Abstract In a previous humorous note, I outlined twelve ways in which performance figures for scientific supercomputers can be distorted. In this paper, the problem of potentially mis- leading performance reporting is discussed in detail. Included are some examples that have appeared in recent published scientific papers. This paper also includes some pro- posed guidelines for reporting performance, the adoption of which would raise the level of professionalism and reduce the level of confusion in the field of supercomputing. The author is with the Numerical Aerodynamic Simulation (NAS) Systems Division at NASA Ames Research Center, Moffett Field, CA 94035. 1 1. Introduction Many readers may have read my previous article “Twelve Ways to Fool the Masses When Giving Performance Reports on Parallel Computers” [5]. The attention that this article received frankly has been surprising [11]. Evidently it has struck a responsive chord among many professionals in the field who share my concerns. The following is a very brief summary of the “Twelve Ways”: 1. Quote only 32-bit performance results, not 64-bit results, and compare your 32-bit results with others’ 64-bit results. 2. Present inner kernel performance figures as the performance of the entire application. 3. Quietly employ assembly code and other low-level language constructs, and compare your assembly-coded results with others’ Fortran or C implementations. 4. Scale up the problem size with the number of processors, but don’t clearly disclose this fact.
    [Show full text]
  • Half Adder, Which Finds the Sum of Two Bits
    CMSC 313 COMPUTER ORGANIZATION & ASSEMBLY LANGUAGE PROGRAMMING LECTURE 21, SPRING 2013 TOPICS TODAY • Circuits for Addition • Standard Logic Components • Logisim Demo CIRCUITS FOR ADDITION 3.5 Combinational Circuits • Combinational logic circuits give us many useful devices. • One of the simplest is the half adder, which finds the sum of two bits. • We can gain some insight as to the construction of a half adder by looking at its truth table, shown at the right. 30 Half Adder • Inputs: A and B • Outputs: S = lower bit of A + B, cout = carry bit A B S cout 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 • Using Sum-of-Products: S = AB + AB, cout = AB. • Alternatively, we could use XOR: S = A ⊕ B. ! ! ! ! 1 3.5 Combinational Circuits • As we see, the sum can be found using the XOR operation and the carry using the AND operation. 31 3.5 Combinational Circuits • We can change our half adder into to a full adder by including gates for processing the carry bit. • The truth table for a full adder is shown at the right. 32 Full Adder • Inputs: A, B and cin • Outputs: S = lower bit of A + B, cout = carry bit A B cin S cout 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 • S = A BC + ABC + AB C + ABC = A ⊕ B ⊕ C.
    [Show full text]
  • Intel Xeon & Dgpu Update
    Intel® AI HPC Workshop LRZ April 09, 2021 Morning – Machine Learning 9:00 – 9:30 Introduction and Hardware Acceleration for AI OneAPI 9:30 – 10:00 Toolkits Overview, Intel® AI Analytics toolkit and oneContainer 10:00 -10:30 Break 10:30 - 12:30 Deep dive in Machine Learning tools Quizzes! LRZ Morning Session Survey 2 Afternoon – Deep Learning 13:30 – 14:45 Deep dive in Deep Learning tools 14:45 – 14:50 5 min Break 14:50 – 15:20 OpenVINO 15:20 - 15:45 25 min Break 15:45 – 17:00 Distributed training and Federated Learning Quizzes! LRZ Afternoon Session Survey 3 INTRODUCING 3rd Gen Intel® Xeon® Scalable processors Performance made flexible Up to 40 cores per processor 20% IPC improvement 28 core, ISO Freq, ISO compiler 1.46x average performance increase Geomean of Integer, Floating Point, Stream Triad, LINPACK 8380 vs. 8280 1.74x AI inference increase 8380 vs. 8280 BERT Intel 10nm Process 2.65x average performance increase vs. 5-year-old system 8380 vs. E5-2699v4 Performance varies by use, configuration and other factors. Configurations see appendix [1,3,5,55] 5 AI Performance Gains 3rd Gen Intel® Xeon® Scalable Processors with Intel Deep Learning Boost Machine Learning Deep Learning SciKit Learn & XGBoost 8380 vs 8280 Real Time Inference Batch 8380 vs 8280 Inference 8380 vs 8280 XGBoost XGBoost up to up to Fit Predict Image up up Recognition to to 1.59x 1.66x 1.44x 1.30x Mobilenet-v1 Kmeans Kmeans up to Fit Inference Image up to up up Classification to to 1.52x 1.56x 1.36x 1.44x ResNet-50-v1.5 Linear Regression Linear Regression Fit Inference Language up to up to up up Processing to 1.44x to 1.60x 1.45x BERT-large 1.74x Performance varies by use, configuration and other factors.
    [Show full text]
  • Chapter 4 Data-Level Parallelism in Vector, SIMD, and GPU Architectures
    Computer Architecture A Quantitative Approach, Fifth Edition Chapter 4 Data-Level Parallelism in Vector, SIMD, and GPU Architectures Copyright © 2012, Elsevier Inc. All rights reserved. 1 Contents 1. SIMD architecture 2. Vector architectures optimizations: Multiple Lanes, Vector Length Registers, Vector Mask Registers, Memory Banks, Stride, Scatter-Gather, 3. Programming Vector Architectures 4. SIMD extensions for media apps 5. GPUs – Graphical Processing Units 6. Fermi architecture innovations 7. Examples of loop-level parallelism 8. Fallacies Copyright © 2012, Elsevier Inc. All rights reserved. 2 Classes of Computers Classes Flynn’s Taxonomy SISD - Single instruction stream, single data stream SIMD - Single instruction stream, multiple data streams New: SIMT – Single Instruction Multiple Threads (for GPUs) MISD - Multiple instruction streams, single data stream No commercial implementation MIMD - Multiple instruction streams, multiple data streams Tightly-coupled MIMD Loosely-coupled MIMD Copyright © 2012, Elsevier Inc. All rights reserved. 3 Introduction Advantages of SIMD architectures 1. Can exploit significant data-level parallelism for: 1. matrix-oriented scientific computing 2. media-oriented image and sound processors 2. More energy efficient than MIMD 1. Only needs to fetch one instruction per multiple data operations, rather than one instr. per data op. 2. Makes SIMD attractive for personal mobile devices 3. Allows programmers to continue thinking sequentially SIMD/MIMD comparison. Potential speedup for SIMD twice that from MIMID! x86 processors expect two additional cores per chip per year SIMD width to double every four years Copyright © 2012, Elsevier Inc. All rights reserved. 4 Introduction SIMD parallelism SIMD architectures A. Vector architectures B. SIMD extensions for mobile systems and multimedia applications C.
    [Show full text]
  • Lecture 4 Adders
    Lecture 4 Adders Computer Systems Laboratory Stanford University [email protected] Copyright © 2006 Mark Horowitz Some figures from High-Performance Microprocessor Design © IEEE M Horowitz EE 371 Lecture 4 1 Overview • Readings • Today’s topics – Fast adders generally use a tree structure for parallelism – We will cover basic tree terminology and structures – Look at a few example adder architectures – Examples will spill into next lecture as well M Horowitz EE 371 Lecture 4 2 Adders • Task of an adder is conceptually simple – Sum[n:0]=A[n:0]+B[n:0]+C0 – Subtractors also very simple: -B = ~B+1, so invert B and set C0=1 • Per bit formulas –Sumi = Ai XOR Bi XOR Ci – Couti = Ci+1 = majority(Ai,Bi,Ci) • Fundamental problem is calculating the carry to the nth bit – All carry terms are dependent on all previous terms – So LSB input has a fanout of n • And an absolute minimum of log4n FO4 delays without any logic M Horowitz EE 371 Lecture 4 3 Single-Bit Adders • Adders are chock-full of XORs, which make them interesting – One of the few circuits where pass-gate logic is attractive – A complicated differential passgate logic (DPL) block from the text Lousy way to draw a pair of inverters M Horowitz EE 371 Lecture 4 4 G and P and K, Oh My! • Most fast adders “G”enerate, “P”ropagate, or “K”ill the carry – Usually only G and P are used; K only appears in some carry chains • When does a bit Generate a carry out? –Gi = Ai AND Bi – If Gi is true, then Couti = Ci+1 is forced to be true • When does a bit Propagate a carry in to the carry out? –Pi
    [Show full text]