DOCSLIB.ORG

PROGRAMMABLE ARRAY LOGIC the PAL Device Is a Special Case of PLA Which Has a Programmable and Array and a Fixed OR Array

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
PROGRAMMABLE ARRAY LOGIC the PAL Device Is a Special Case of PLA Which Has a Programmable and Array and a Fixed OR Array PROGRAMMABLE ARRAY LOGIC The PAL device is a special case of PLA which has a programmable AND array and a fixed OR array. The basic structure of Rom is same as PLA. It is cheap compared to PLA as only the AND array is programmable. It is also easy to program a PAL compared to PLA as only AND must be programmed. The figure 1 below shows a segment of an unprogrammed PAL. The input buffer with non inverted and inverted outputs is used, since each PAL must drive many AND Gates inputs. When the PAL is programmed, the fusible links (F1, F2, F3…F8) are selectively blown to leave the desired connections to the AND Gate inputs. Connections to the AND Gate inputs in a PAL are represented by Xs , as shown here: Figure 1: segment of an unprogrammed and programmed PAL. As an example, we will use the PAL segment of figure 1 to realize the function I1I2’+I 1I2. the Xs indicate that the I 1 and I 2’ lines are connected to the first AND Gate, and the I 1’ and I 2 lines are connected to the other Gate. Typical combinational PAL have 10 to 20 inputs and from 2 to 10 outputs with 2 to 8 AND gates driving each OR gate. PALs are also available which contain D flip-flops with inputs driven from the programming array logic. Such PAL provides a convenient way of realizing sequential networks. Figure 2 below shows a segment of a sequential PAL. The D flip-flop is driven from the OR gate, which is fed by two AND gates. The flip-flop output is fed back to the programmable AND array through a buffer. Thus the AND gate inputs can be connected to A, A’, B, B’, Q, or Q’. The Xs on the diagram show the realization of the next-state equation. Q+ = D = A’BQ’ + AB’Q The flip-flop output is connected to an inverting tristate buffer, which is enabled when EN = 1 Figure 2 Segment of a Sequential PAL Figure 3 below shows a logic diagram for a typical sequential PAL, the 16R4. This PAL has an AND gate array with 16 input variables, and it has 4 D flip-flops. Each flip-flop output goes through a tristate-inverting buffer (output pins 14-17). One input (pin 11) is used to enable these buffers. The rising edge of a common clock (pin 1) causes the flip-flops to change the state. Each D flip-flop input is driven from an OR gate, and each OR gate is fed from 8 AND gates. The AND gate inputs can come from the external PAL inputs (pins2-9) or from the flip-flop outputs, which are fed back internally. In addition there are four input/output (i/o) terminals (pins 12,13,18 and 19), which can be used as either network outputs or as inputs to the AND gates. Thus each AND gate can have a maximum of 16 inputs (8 external inputs, 4 inputs fed back from the flip-flop outputs, and 4 inputs from the i/o terminals). When used as an output, each I/O terminal is driven from an inverting tristate buffer. Each of these buffers is fed from an OR gate and each OR gate is fed from 7 AND gates. An eighth AND gate is used to enable the buffer. Figure 3: logic diagram for 16R4 pal When the 16R4 PAL is used to realize a sequential network, the I/O terminals are normally used for the z outputs. Thus, a single 16R4 with no additional logic could realize a sequential network with up to 8 inputs, 4 outputs, and 16 states. Each next state equation could contain up to 8 terms, and each output equation could contain up to 7 terms. As an example, we will realize the BCD to Excess-3 code converter using three flip-flops to store Q1,Q2 and Q3, and the array logic that drives these flip-flops is programmed to realize D1, D2 and D3, as shown in figure 3 .The Xs on the diagram indicate the connections to the AND-gate inputs. An X inside an AND gate indicates that the gate is not used. For D3, three AND gates are used, and the function realized is D3 = Q1Q2Q3 + X’Q1Q3’ + XQ1’Q2’ The flip-flop outputs are not used externally, so the output buffers are disabled. Since the Z output comes through the inverting buffer, the array logic must realize Z’ = (X + Q3)(X’ + Q3’) = XQ3’ + X’Q3 The z output buffer is permanently enabled in this example, so there are no connections to the AND gate that drives the enable input, in which case the AND gate output is logic1. When designing with PALS, we must simplify our logic equations and try to fit them in one or more PALs. Unlike the more general PLA, the AND terms cannot be shared among two or more OR gates; therefore, each function to be realized can be simplified by itself without regard to common terms. For a given type of PAL the number of AND terms that feed each output OR gate is fixed and limited. If the number of AND terms in a simplified function is too large, we may be forced to choose a PAL with more OR-gate inputs and fewer outputs. Computer aided design programs for PAL s are widely available. Such programs accept logic equations, truth tables, state graphs, or state tables as inputs and automatically generate the required fused patterns. These patterns can then be downloaded into a PLD programmer, which will blow the required, fuses and verify the operation of the PAL. Other sequential programmable logic devices (PLDs) The 16R4 is an example of a simple sequential PLD. As the integrated technology has improved, a wide variety of other PLDs have become available. Some of these are based on extensions of PAL concept, and others have based on gate arrays. The 22CEV10 is a CMOS electrically erasable PLD that can be used to realize both combinational and sequential networks. • It has 12 dedicated input pins and 10 pins that can be programmed as either inputs or outputs. • It contains 10 d flip-flops and 10 OR gates. • The number of AND gates that feed each OR gate ranges from 8 to 16. • Each OR gate drives an output logic macrocell. • Each macrocell contains one of the 10 D flip-flops. • The flip-flops have the common clock, a common asynchronous reset (AR) input and a common synchronous preset (SP) input. Similarly, 22V10 indicates a versatile PAL with a total of 22 input and output pins, 10 of which are bi-directional I/O (input/output) pins. Figure 4: block diagram for 22CEV10 Figure 4 shows the details of a 22CEV10 output macrocell. The connections to the output pins are controlled by programming the macrocell. The output mux controls inputs S1 and S0 select one of the data inputs. For example, S1S0 = 10 selects data input 2. Each macrocell has two programmable interconnect bits. S1 or S0 is connected to ground (logic 0) when the corresponding bit is programmed. Erasing a bit disconnects the control line (S1 or S0) from ground and allows it to float to Vcc (logic 1). When S1 = 1, the flip flop is bypassed, and the output is from the OR gate. The OR gate output is connected to the I/O pin through the multiplexer and the output buffer. The OR gate is also fed back so that it can be used as an input to the AND gate array. If S1 = 0, then the flip-flop output is connected to the output pin, and it is also fed back so that it can be used for AND gate inputs. when S0 = 1, the output is not inverted, so it is active high. When S0 = 0 ,the output is inverted, so it is active low. The output pin is driven from the tristate-inverting buffer. When the buffer output is in the high impedance state, the OR gates and the flip-flops are disconnected from the output pin, and the pin can be used as input. The dashed lines on figure 5 show the path when both S0 and S1 are 1. Note that in the first case the flip flop Q output is inverted by the output buffer, and in the second case the OR gate output is inverted twice so there is no net inversion. Figure 5: internal diagram of macro cell of 22CEV10 Design a sequential traffic-light controller using 22v10 Traffic light controller Consider the design of a sequential traffic-light controller for the intersection of “A” street and “B” street. Features of the traffic-light controller Each street has traffic sensors, which detect the presence of vehicles approaching or stopped at the intersection. Sa =1 means a vehicle is approaching on “A” street, and Sb=1 means a vehicle is approaching on “B” street. “A” street is a main street and has a green light until the car approaches on “B”. Then the light changes and “B” has a green light. At the end of 50 seconds, the light changes back unless there is a car on “B ” street and none on “A”, in which case the “B” cycle is extended to another 10 more seconds. When “A” is green, it remains green at least 60 seconds, and then the lights change only when the car approaches on “B”. Figure 6 shows the external connections to the controller.
Load more

Recommended publications
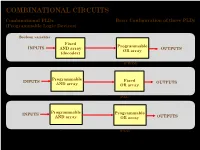
  • COMBINATIONAL CIRCUITS Combinational Plds Basic Configuration of Three Plds (Programmable Logic Devices)
    COMBINATIONAL CIRCUITS Combinational PLDs Basic Configuration of three PLDs (Programmable Logic Devices) Boolean variables Fixed Programmable INPUTS AND array OUTPUTS OR array (decoder) Programmable Read-Only Memory (PROM) Programmable INPUTS Fixed OUTPUTS AND array OR array Programmable Array Logic (PAL) Programmable INPUTS Programmable AND array OR array OUTPUTS (Field) Programmable Logic Array (PLA) 1 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Two-level AND-OR Arrays (Programmable Logic Devices) F (C,B, A) = CBA + CB A A AND B + V B C A C B F C F AND F + V 1 B OR C Multiple functions Simplified equivalent circuit for two-level AND-OR array 2 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Field-programmable AND and OR Arrays (Programmable Logic Devices) Field-programmable logic elements are devices that contain uncommitted AND/OR arrays that are (programmed) configured by the designer. + V + V A A F (C,B, A) F (C,B, A) = CBA B B C C Unprogrammed AND array Fuse can be "blown" by passing a high current through it. 3 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Field-programmable AND and OR Arrays (Programmable Logic Devices) F (P1 ,P2 ,P3 ) = P1 + P3 P1 P1 P2 P2 P3 P3 F F (P1 ,P2 ,P3 ) Unprogrammed OR array Programmed OR array P1 P2 P3 P1 + P3 4 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Output Polarity Options (Programmable Logic Devices) I1 Ik Active high Active low Complementary outputs Programmable polarity P P 1 m + V 5 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Bidirectional Pins and Feed back Lines (Programmable Logic Devices) I1 Ik Feedback IOm Three-state driver 6 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs PLA (Programmable Logic Array) (Programmable Logic Devices) If we use ROM to implement the Boolean function we will waste the silicon area.
    [Show full text]
  • Development of a Programmable Array Logic
    i DEVELOPMENT OF A PROGRAMMABLE ARRAY LOGIC PROGRAMMER USING A HOME COMPUTER by GERT DANIEL JORDAAN Dissertation submitted in compliance with the requirements for the MASTER'S DIPLOMA in TECHNOLOGY in the Department of Electronics at the TECHNIKON O. F . S . OCTOBER, 1988. Supervisor: Prof. F.W. Bruwer Co-supervisor: Mr. B. de Witt © Central University of Technology, Free State ACKNOWLEDGEMENTS I would like to thank the following persons without whose help this project could hardly have been completed: The supervisor, prof. F.W. Bruwer, and co-supervisor, mr. 8. de Witt, for help and guidance during the course of the project. Mr. H.F. Coetzer for technical as well as philolog ical assistance. It is really appreciated that time could be found in his very full schedule, for this assistance. Dr. C.A.J. van Rensburg for his per_onal interest in the research project and for continuous encouragement and help. Dr. J. van der Mer-we for his assistance - in particular with respect to the registration and other administrative aspects of the project. / Miss M. du Toit who was largely responsible for the word processing. For the guidance provided by my parents and the opportuni- ties which they afforded me. My children, Tania, Johan, Madelie and Lourens,. whose main contribution was to have to forego much of my attention and time for such a long period. Last, but not least, my wife, Christa, for her encouragement and understanding. © Central University of Technology,ii Free State CONTENTS PAGE Cilapter 1 1 Intr--oduc tion 1.1 Recent Trends in Electronics 1 1.2 Problem Investigated 1 1.3 Development of PAL Programmer 3 1.3.1 Generation of Fuse Map 3 1.3.2 Programming of Programmable Array Logic 3 Devices 1 .
    [Show full text]
  • RESEARCH INSIGHTS – Hardware Design: FPGA Security Risks
    RESEARCH INSIGHTS Hardware Design: FPGA Security Risks www.nccgroup.trust CONTENTS Author 3 Introduction 4 FPGA History 6 FPGA Development 10 FPGA Security Assessment 12 Conclusion 17 Glossary 18 References & Further Reading 19 NCC Group Research Insights 2 All Rights Reserved. © NCC Group 2015 AUTHOR DUNCAN HURWOOD Duncan is a senior consultant at NCC Group, specialising in telecom, embedded systems and application review. He has over 18 years’ experience within the telecom and security industry performing almost every role within the software development cycle from design and development to integration and product release testing. A dedicated security assessor since 2010, his consultancy experience includes multiple technologies, languages and platforms from web and mobile applications, to consumer devices and high-end telecom hardware. NCC Group Research Insights 3 All Rights Reserved. © NCC Group 2015 GLOSSARY AES Advanced encryption standard, a cryptography OTP One time programmable, allowing write once cipher only ASIC Application-specific integrated circuit, non- PCB Printed circuit board programmable hardware logic chip PLA Programmable logic array, forerunner of FPGA Bitfile Binary instruction file used to program FPGAs technology CLB Configurable logic block, an internal part of an PUF Physically unclonable function FPGA POWF Physical one-way function CPLD Complex programmable logic device PSoC Programmable system on chip, an FPGA and EEPROM Electronically erasable programmable read- other hardware on a single chip only memory
    [Show full text]
  • Programmable Logic Design Quick Start Hand Book
    Second Edition Programmable Logic Design Quick Start Hand Book By Karen Parnell & Nick Mehta January 2002 ABSTRACT Whether you design with discrete logic, base all of your designs on microcontrollers, or simply want to learn how to use the latest and most advanced programmable logic software, you will find this book an interesting insight into a different way to design. Programmable logic devices were invented in the late seventies and since then have proved to be very popular and are now one of the largest growing sectors in the semiconductor industry. Why are programmable logic devices so widely used? Programmable logic devices provide designers ultimate flexibility, time to market advantage, design integration, are easy to design with and can be reprogrammed time and time again even in the field to upgrade system functionality. This book was written to complement the popular XilinxÒ Campus Seminar series but can also be used as a stand-alone tutorial and information source for the first of your many programmable logic designs. After you have finished your first design this book will prove useful as a reference guide or quick start handbook. The book details the history of programmable logic, where and how to use them, how to install the free, full functioning design software (Xilinx WebPACKä ISE included with this book) and then guides you through your first of many designs. There are also sections on VHDL and schematic capture design entry and finally a data bank of useful applications examples. We hope you find the book practical, informative and above all easy to use.
    [Show full text]
  • CPLD and FPGA Architectures
    ECE 428 Programmable ASIC Design CPLD and FPGA Architectures Haibo Wang ECE Department Southern Illinois University Carbondale, IL 62901 3-1 Definitions Field Programmable Device (FPD): — a general term that refers to any type of integrated circuit used for implementing digital hardware, where the chip can be configured by the end user to realize different designs. Programming of such a device often involves placing the chip into a special programming unit, but some chips can also be configured “in-system”. Another name for FPDs is programmable logic devices (PLDs). Source: S. Brown and J. Rose, FPGA and CPLD Architectures: A Tutorial, IEEE Design and Test of Computer, 1996 3-2 Classifications PLA — a Programmable Logic Array (PLA) is a relatively small FPD that contains two levels of logic, an AND- plane and an OR-plane, where both levels are programmable PAL — a Programmable Array Logic (PAL) is a relatively small FPD that has a programmable AND-plane followed by a fixed OR-plane SPLD — refers to any type of Simple PLD, usually either a PLA or PAL CPLD — a more Complex PLD that consists of an arrangement of multiple SPLD-like blocks on a single chip. FPGA — a Field-Programmable Gate Array is an FPD featuring a general structure that allows very high logic capacity. 3-3 PLA Programmable AND Plane Programmable OR Plane Programmable Node Un-programmed Connect Disconnect X Y O1 O2 O3 O4 X XY Y XY XY XY XX YY 3-4 PLA Programmable AND Plane Programmable OR Plane YZ XZ XYZ XY XY Z XY+YZ ?? XZ+XYZ 3-5 PAL Programmable AND Plane Fix OR Plane X Y O1 O2 O3 O4 3-6 PAL with Logic Expanders Programmable AND Plane Fix OR Plane ? Logic expanders 3-7 PLA v.s.
    [Show full text]
  • High-Performance Impact-X Programmable
    OBSOLETE - No Longer Available TIBPAL16L8-5C, TIBPAL16R4-5C, TIBPAL16R6-5C, TIBPAL16R8-5C TIBPAL16L8-7M, TIBPAL16R4-7M, TIBPAL16R6-7M, TIBPAL16R8-7M HIGH-PERFORMANCE IMPACT-X PAL CIRCUITS SRPS011D – D3359, OCTOBER 1989 – REVISED SEPTEMBER 1992 • High-Performance Operation: TIBPAL16L8’ C SUFFIX . J OR N PACKAGE fmax (no feedback) M SUFFIX . J PACKAGE TIBPAL16R’ -5C Series . 125 MHz Min (TOP VIEW) TIBPAL16R’ -7M Series . 100 MHz Min f (internal feedback) max I 1 20 V TIBPAL16R’ -5C Series . 125 MHz Min CC I 2 19 O TIBPAL16R’ -7M Series . 100 MHz Min I 3 18 I/O f (external feedback) max I TIBPAL16R’ -5C Series . 117 MHz Min 4 17 I/O I TIBPAL16R’ -7M Series . 74 MHz Min 5 16 I/O I Propagation Delay 6 15 I/O I TIBPAL16L8-5C Series . 5 ns Max 7 14 I/O TIBPAL16L8-7M Series . 7 ns Max I 8 13 I/O TIBPAL16R’ -5C Series I 9 12 O (CLK-to-Q) . 4 ns Max GND 10 11 I TIBPAL16R ’ -7M Series (CLK-to-Q) . 6.5 ns Max • Functionally Equivalent, but Faster than, Existing 20-Pin PLDs TIBPAL16L8’ • Preload Capability on Output Registers C SUFFIX . FN PACKAGE Simplifies Testing M SUFFIX . FK PACKAGE • Power-Up Clear on Registered Devices (All (TOP VIEW) Register Outputs are Set Low, but Voltage CC I I I O Levels at the Output Pins Go High) V • Package Options Include Both Plastic and 3 2 1 20 19 I I/O Ceramic Chip Carriers in Addition to Plastic 4 18 I/O and Ceramic DIPs I 5 17 • I 6 16 I/O Security Fuse Prevents Duplication I 7 15 I/O I 8 14 I/O I/O I 3-STATE REGISTERED 910111213 PORT DEVICE INPUTS O OUTPUTS Q OUTPUTS S I I O ’PAL16L8 10 2 0 6 I/O ’PAL16R4 8 0 4 (3-state buffers) 4 GND ’PAL16R6 8 0 6 (3-state buffers) 2 ’PAL16R8 8 0 8 (3-state buffers) 0 Pin assignments in operating mode description These programmable array logic devices feature high speed and functional equivalency when compared with currently available devices.
    [Show full text]
  • Ch7. Memory and Programmable Logic
    EEA091 - Digital Logic 數位邏輯 Chapter 7 Memory and Programmable Logic 吳俊興 國立高雄大學 資訊工程學系 2006 Chapter 7 Memory and Programmable Logic 7-1 Introduction 7-2 Random-Access Memory 7-3 Memory Decoding 7-4 Error Detection and Correction 7-5 Read-Only Memory 7-6 Programmable Logic Array 7-7 Programmable Array Logic 7-8 Sequential Programmable Devices 7-1 Introduction • Memory unit –a collection of cells capable of storing a large quantity of binary information and • to which binary information is transferred for storage • from which information is available when needed for processing –together with associated circuits needed to transfer information in and out of the device • write operation: storing new information into memory • read operation: transferring the stored information out of the memory • Two major types –RAM (Random-access memory): Read + Write • accept new information for storage to be available later for use –ROM (Read-only memory): perform only read operation Programmable Logic Device •Programmable logic device (PLD) –an integrated circuit with internal logic gates • hundreds to millions of gates interconnected through hundreds to thousands of internal paths –connected through electronic paths that behave similar to fuse • In the original state, all the fuses are intact –programming the device • blowing those fuse along the paths that must be removed in order to obtain particular configuration of the desired logic function •Types –Read-only Memory (ROM, Section 7-5) –programmable logic array (PLA, Section 7-6) –programmable array
    [Show full text]
  • No Slide Title
    ECEN 248 –Introduction to Digital Systems Design (Spring 2008) (Sections: 501, 502, 503, 507) Prof. Xi Zhang ECE Dept, TAMU, 333N WERC http://www.ece.tamu.edu/~xizhang/ECEN248 Programmable logic device (PLD) A PLD is a general-purpose chip for implementing logic circuit. It contains a collection of logic circuit elements that can be customized in different ways. A PLD can be viewed as a “black box” that contains logic gates and programmable switches. The programmable switches allow the logic gates inside the PLD to be connected together to implement logic circuits. Programmable logic device as a black box Logic gates Inputs and Outputs (logic variables) programmable (logic functions) switches Figure 3.24. Programmable logic device as a black box. Programmable logic devices Different types of PLD Simple PLD (SPLD) Programmable logic array (PLA) Programmable array logic (PAL) Complex PLD (CPLD) Field-programmable gate arrays (FPGA) Programmable logic array (PLA) x1 x2 xn PLA is developed based on the sum-of-product form. A PLA includes a circuit Input buffers block called an AND plane and (or AND array) and a inverters circuit block called an OR plane (or OR array). x1 x1 xn xn Æ Input Buffer/inverters P Æ And plane Æ OR plane 1 Æ Output AND plane OR plane Pk f1 fm Figure 3.25. General structure of a PLA. Gate-level diagram of a PLA x1 x2 x3 Output of And plane: Programmable connections P1= x 1 x 2 OR plane P1 P2= x 1 x 3 P2 P3= x 1 x 2 x 3 P4= x 1 x 3 P3 Output of OR plane: P4 f1 x 1= x 2+ x 1 x 3+ x 1 x 2 x 3 AND plane f2 x 1= x 2+ x 1 x 2+ x 3 x 1 x 3 f1 f2 Figure 3.26.
    [Show full text]
  • National Semiconductor Sales Lead Temperature Office/Distributors for Availability and Specifications
    National preliminary Semiconductor PALI 0/10016PE8-3 (PLCC Only) 3 ns ECL ASPECT™ Programmable Array Logic ECL PAL10/10016PE8-3 ECL General Description The PAL10/10016PE8-3 is a member of the National Semi­ product term. Each output function is provided with output conductor 28-pin high speed ECL PAL® family. This device polarity fuses. These fuses permit the designer to configure utilizes National Semiconductor’s ASPECT (Advanced Sin­ each output independently to produce either a logic high (by gle Poly Emitter Coupled Technology) process with a newly leaving the fuse intact) or a logic low (by programming the developed tungsten fuse technology to provide the highest- fuse) when the equation defining that output is satisfied. speed user-programmable replacements for conventional Programming equipment and software make PAL design de­ ECL SSI-MSI logic with significant chip-count reduction. The velopment quick and easy. Programming is accomplished JEDEC fuse-map format and programming algorithm of this using TTL voltage levels and is therefore supported by in­ device is compatible with those of all prior ECL PAL prod­ dustry standard conventional TTL PLD programmers. After ucts from National. programming and verifying the logic array, an additional se­ Programmable logic devices provide convenient solutions curity fuse may be programmed to prevent direct copying of for a wide variety of applications— specific functions, includ­ proprietary logic designs. ing random logic, custom decoders, state machines, etc. By programming fuse links to configure AND/OR gate connec­ Features tions, the system designer can implement custom logic as ■ High speed: tpp 3 ns max convenient sum-of-products Boolean functions.
    [Show full text]
  • Field Programmable Gate Array (FPGA)
    Field Programmable Gate Array (FPGA) Wae Wolf, FPGA Based “ste Desig , 2004, Prentice Hall. INTRODUCTION TO PROGRAMMABLE LOGIC • Programmable logic requires both hardware and software. • Programmable logic devices can be programmed to Perform specified logic functions by the manufacturer or by the user. • One advantage of programmable logic over fixed-function logic is that the devices use much less board space for an equivalent amount of logic. • Another advantage is that, with programmable logic, designs can be readily changed without rewiring or replacing components. • Also, a logic design can generally be implemented faster and with less cost with programmable logic than with fixed-function ICs. Types of Programmable logic Devices • Many types of programmable logic are available, ranging from small devices that can replace a few fixed-function devices to complex high-density devices that can replace thousands of fixed-function devices. • Two major categories of user-programmable logic are PLD (programmable logic device) and FPGA (field programmable gate array). • PLDs are either SPLDs (simple PLDs) or CPLDs (complex PLDs). Simple Programmable logic Devices • The SPLD was the original PLD and is still available for small-scale applications. • Generally, an SPLD can replace up to ten fixed-function ICs and their interconnections, depending on the type of functions and the specific SPLD. • Most SPLDs are in one of two categories: PAL and GAL. • A PAL (programmable array logic) is a device that can be programmed one time. It consists of a programmable array of AND gates and a fixed array of OR gates. • A GAL (generic array logic) is a device that is basically a PAL that can be reprogrammed many times.
    [Show full text]
  • Nasa Handbook Nasa-Hdbk 8739.23A Measurement
    NASA HANDBOOK NASA-HDBK 8739.23A National Aeronautics and Space Administration Approved: 02-02-2016 Washington, DC 20546 Superseding: NASA-HDBK-8739.23 With Change 1 NASA COMPLEX ELECTRONICS HANDBOOK FOR ASSURANCE PROFESSIONALS MEASUREMENT SYSTEM IDENTIFICATION: METRIC APPROVED FOR PUBLIC RELEASE – DISTRIBUTION IS UNLIMITED NASA-HDBK 8739.23A—2016-02-02 Mars Exploration Rover (2003) 2 of 161 NASA-HDBK 8739.23A—2016-02-02 DOCUMENT HISTORY LOG Document Status Approval Date Description Revision Initial Release Baseline 2011-02-16 (JWL4) Editorial correction to page 2 figure caption Change 1 2011-03-29 (JWL4) Significant changes were made in this revision, including: expanded content; reflected terminology and technology from the NASA-HDBK-4008, Programmable Revision A 2016-02-02 Logic Devices (PLD) Handbook (released in 2013); eliminated duplication with the PLD Handbook; and, incorporated other clarifications and corrections. (MW) 3 of 161 NASA-HDBK 8739.23A—2016-02-02 This page intentionally left blank. 4 of 161 NASA-HDBK 8739.23A—2016-02-02 This page intentionally left blank. 6 of 161 NASA-HDBK 8739.23A—2016-02-02 TABLE OF CONTENTS 1 OVERVIEW ................................................................................................................ 12 1.1 Purpose .......................................................................................................................... 12 1.2 Scope ............................................................................................................................. 12 1.3 Anticipated
    [Show full text]
  • Introduction to Programmable Logic Devices
    Introduction to Programmable Logic Devices © 2015 Kael HANSON 1 Arbitrary Logic Tables ABC Minterm Maxterm P 0 0 0 A¯ · B¯ · C¯ A + B + C 0 Here we briefly review two strategies used in programmable 0 0 1 A¯ · B¯ · C A + B + C¯ 0 logic devices to realize arbitrary truth tables in digital hard- 0 1 0 A¯ · B · C¯ A + B¯ + C 1 ware: the sum-of-products which uses explicit ANDs and ¯ ¯ ¯ ORs, and the lookup table (LUT) method used in most mod- 0 1 1 A · B · C A + B + C 1 ern FPGAs and CPLDs. 1 0 0 A · B¯ · C¯ A¯ + B + C 0 1 0 1 A · B¯ · C A¯ + B + C¯ 1 · · ¯ ¯ ¯ 1.1 Sum of Products, &c. 1 1 0 A B C A + B + C 0 1 1 1 A · B · C A¯ + B¯ + C¯ 1 Classic programmable logic devices, PALs, GALs, and older CPLDs, implemented logic functions using combinations Table 1: Minterms and maxterms of 3 logic variables A, B, of ANDs and ORs. An arbitrary function of N boolean and C in a prime number truth table. variables may be expressed as the sum (OR) of product minterms or the product (AND) of sum maxterms, defined below. or POS: Minterm The minterms associated with N boolean vari- P2 = (A + B + C)(A + B + C¯)(A¯ + B + C)(A¯ + B¯ + C): (2) ables, faig are the product terms of all possible combi- N nations of faig and fa¯ig. There are 2 distinct terms. ¯ Perhaps an easier way to think of this is to construct It is easy to show that P1 = P2 using DeMorgan’s identity.
    [Show full text]