DOCSLIB.ORG

Digital System Design with Systemverilog

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Digital System Design with Systemverilog Digital System Design with SystemVerilog Mark Zwoli´nski October 9, 2009 DRAFT 2 DRAFT Contents Preface 19 1 Introduction 25 1.1 Modern digital design . 25 1.2 Designing with hardware description languages . 25 1.2.1 Design automation . 25 1.2.2 What is SystemVerilog? . 26 1.2.3 WhatisVHDL? ...................... 26 1.2.4 Simulation ......................... 27 1.2.5 Synthesis .......................... 27 1.2.6 Reusability ......................... 28 1.2.7 Verification ......................... 28 1.2.8 Designflow......................... 29 1.3 CMOStechnology ......................... 32 1.3.1 Logicgates ......................... 32 1.3.2 ASICsandFPGAs ..................... 33 1.4 Programmablelogic. 38 1.5 Electrical properties . 42 1.5.1 Noisemargins ....................... 42 1.5.2 Fan-out ........................... 44 Summary ................................. 45 Furtherreading .............................. 46 Exercises ................................. 46 2 Combinational logic design 47 2.1 Booleanalgebra........................... 47 2.1.1 Values............................ 47 2.1.2 Operators .......................... 47 2.1.3 Truthtables......................... 48 2.1.4 Rules of Boolean algebra . 49 2.1.5 DeMorgan’slaw ...................... 50 2.1.6 Shannon’s expansion theorem . 50 2.2 Logicgates ............................. 50 DRAFT3 4 CONTENTS 2.3 Combinational logic design . 52 2.3.1 Logic minimization . 53 2.3.2 Karnaughmaps....................... 54 2.4 Timing................................ 59 2.5 Numbercodes............................ 60 2.5.1 Integers........................... 63 2.5.2 Fixed point numbers . 63 2.5.3 Floating point numbers . 64 2.5.4 Alphanumeric characters . 64 2.5.5 Graycodes ......................... 64 2.5.6 Paritybits.......................... 65 Summary ................................. 66 Furtherreading .............................. 66 Exercises ................................. 66 3 Combinational logic 69 3.1 Modulesandfiles .......................... 69 3.2 Identifiers, spaces and comments . 70 3.3 Basicgatemodels.......................... 71 3.4 Asimplenetlist ........................... 72 3.5 Logicvalues............................. 73 3.6 Continuous assignments . 73 3.6.1 SystemVerilog operators . 74 3.7 Delays................................ 75 3.8 Parameters.............................. 77 3.9 Testbenches ............................. 78 Summary ................................. 79 Furtherreading .............................. 79 Exercises ................................. 79 4 Combinational building blocks 81 4.1 Multiplexers............................. 81 4.1.1 2to1multiplexer.. ..... ...... ..... .... 81 4.1.2 4to1multiplexer.. ..... ...... ..... .... 82 4.2 Decoders .............................. 83 4.2.1 2-4decoder......................... 83 4.2.2 Parameterizable decoder . 85 4.2.3 Seven-segment decoder . 86 4.3 Priorityencoder........................... 88 4.3.1 Don’t cares and uniqueness . 88 4.4 Adders................................ 89 4.4.1 Functional model . 89 4.4.2 Rippleadder ........................ 90 4.4.3DRAFT Tasks ............................ 91 CONTENTS 5 4.5 Paritychecker............................ 92 4.6 Three state buffers . 94 4.6.1 Multi-valued logic . 94 4.7 Testbenches for combinational blocks . 95 Summary ................................. 97 Furtherreading .............................. 97 Exercises ................................. 97 5 Sequential logic blocks 99 5.1 Latches ............................... 99 5.1.1 SRlatch........................... 99 5.1.2 Dlatch ........................... 101 5.2 Flip-flops .............................. 102 5.2.1 Edge-triggered D flip-flop . 102 5.2.2 Asynchronous set and reset . 102 5.2.3 Synchronous set and reset and clock enable . 104 5.3 JKandTflip-flops ......................... 106 5.4 Registers and shift registers . 108 5.4.1 Multiple bit register . 108 5.4.2 Shift registers . 108 5.5 Counters............................... 111 5.5.1 Binary counter . 111 5.5.2 Johnson counter . 114 5.5.3 Linear feedback shift register . 116 5.6 Memory............................... 119 5.6.1 ROM ............................ 119 5.6.2 StaticRAM......................... 120 5.6.3 SynchronousRAM . 121 5.7 Sequential multiplier . 122 5.8 Testbenches for sequential building blocks . 124 5.8.1 Clock generation . 124 5.8.2 Reset and other deterministic signals . 125 5.8.3 Checking responses . 126 Summary ................................. 128 Furtherreading .............................. 128 Exercises ................................. 128 6 Synchronous sequential design 131 6.1 Synchronous sequential systems . 131 6.2 Models of synchronous sequential systems . 132 6.2.1 Moore and Mealy machines . 132 6.2.2 State registers . 132 6.2.3 Design of a three-bit counter . 133 6.3 Algorithmic stateDRAFT machines . 135 6 CONTENTS 6.4 Synthesis from ASM charts . 140 6.4.1 Hardware implementation . 140 6.4.2 State assignment . 143 6.4.3 State minimization . 148 6.5 State machines in SystemVerilog . 153 6.5.1 Afirstexample ... ..... ...... ..... .... 153 6.5.2 A sequential parity detector . 156 6.5.3 Vending machine . 157 6.5.4 Storingdata......................... 159 6.6 Testbenches for state machines . 161 Summary ................................. 162 Furtherreading .............................. 162 Exercises ................................. 162 7 Complex sequential systems 167 7.1 Linked state machines . 167 7.2 Datapath/controller partitioning . 168 7.3 Instructions ............................. 174 7.4 A simple microprocessor . 175 7.5 Microprocessor model . 180 Summary ................................. 189 Furtherreading .............................. 189 Exercises ................................. 189 8 Writing testbenches 191 8.1 Basic testbenches . 192 8.1.1 Clock generation . 192 8.1.2 Reset and other deterministic signals . 193 8.1.3 Monitoring responses . 193 8.1.4 Dumping responses . 193 8.1.5 Test vectors from a file . 194 8.2 Testbench structure . 194 8.2.1 Programs .......................... 196 8.3 Constrained random stimulus generation . 197 8.3.1 Object-oriented programming . 198 8.3.2 Randomization . 199 8.4 Assertion-based verification . 201 Summary ................................. 205 Furtherreading .............................. 206 ExercisesDRAFT ................................. 206 CONTENTS 7 9 SystemVerilog simulation 209 9.1 Event-driven simulation . 209 9.2 SystemVerilog simulation . 213 9.3 Races ................................ 215 9.3.1 Avoiding races . 216 9.4 Delaymodels ............................ 217 9.5 Simulatortools ........................... 218 Summary ................................. 219 Furtherreading .............................. 220 Exercises ................................. 220 10 SystemVerilog synthesis 223 10.1 RTLsynthesis............................ 225 10.1.1 Non-synthesizable SystemVerilog . 225 10.1.2 Inferred flip-flops and latches . 226 10.1.3 Combinational logic . 230 10.1.4 Summary of RTL synthesis rules . 234 10.2 Constraints ............................. 234 10.2.1 Attributes ... ..... ...... ..... ...... 235 10.2.2 Area and structural constraints . 236 10.2.3 full case and parallel case attributes . 238 10.3 SynthesisforFPGAs . 239 10.4 Behavioral synthesis . 242 10.5 Verifying synthesis results . 247 10.5.1 Timing simulation . 250 Summary ................................. 251 Furtherreading .............................. 252 Exercises ................................. 252 11 Testing digital systems 255 11.1 The need for testing . 255 11.2 Faultmodels............................. 256 11.2.1 Single-stuck fault model . 257 11.2.2 PLAfaults ......................... 257 11.3 Fault-oriented test pattern generation . 258 11.3.1 Sensitive path algorithm . 259 11.3.2 Undetectable faults . 260 11.3.3 The D algorithm . 261 11.3.4 PODEM .......................... 264 11.3.5 Fault collapsing . 265 11.4 Fault simulation . 265 11.4.1 Parallel fault simulation . 267 11.4.2 Concurrent fault simulation . 268 Summary .................................DRAFT 269 8 CONTENTS Furtherreading .............................. 269 Exercises ................................. 269 12 Design for testability 275 12.1 Ad hoc testability improvements . 276 12.2 Structured design for test . 276 12.3 Built-in self-test . 279 12.3.1 Example .......................... 281 12.3.2 Built-in logic block observation (BILBO) . 285 12.4 Boundary scan (IEEE 1149.1) . 288 Summary ................................. 295 Furtherreading .............................. 296 Exercises ................................. 296 13 Asynchronous sequential design 299 13.1 Asynchronous circuits . 299 13.2 Analysis of asynchronous circuits . 302 13.2.1 Informal analysis . 302 13.2.2 Formal analysis . 304 13.3 Design of asynchronous circuits . 306 13.4 Asynchronous state machines . 315 13.5 Setup and hold times and metastability . 319 13.5.1 The fundamental mode restriction and synchronous circuits 319 13.5.2 SystemVerilog modeling of setup and hold time violations 320 13.5.3 Metastability . 322 Summary ................................. 323 Furtherreading .............................. 324 Exercises ................................. 324 14 Interfacing with the analog world 327 14.1 Digital to analog converters . 327 14.2 Analog to digital converters . 329 14.3 Verilog-AMS ............................ 332 14.3.1 Verilog-AMS fundamentals . 332 14.3.2 Contribution statements . 334 14.3.3 Mixed-signal modeling . 336 14.4 Phased-locked loops
Load more

Recommended publications
  • Systemverilog
    SystemVerilog ● Industry's first unified HDVL (Hw Description and Verification language (IEEE 1800) ● Major extension of Verilog language (IEEE 1364) ● Targeted primarily at the chip implementation and verification flow ● Improve productivity in the design of large gate-count, IP- based, bus-intensive chips Sources and references 1. Accellera IEEE SystemVerilog page http://www.systemverilog.com/home.html 2. “Using SystemVerilog for FPGA design. A tutorial based on a simple bus system”, Doulos http://www.doulos.com/knowhow/sysverilog/FPGA/ 3. “SystemVerilog for Design groups”, Slides from Doulos training course 4. Various tutorials on SystemVerilog on Doulos website 5. “SystemVerilog for VHDL Users”, Tom Fitzpatrick, Synopsys Principal Technical Specialist, Date04 http://www.systemverilog.com/techpapers/date04_systemverilog.pdf 6. “SystemVerilog, a design and synthesis perspective”, K. Pieper, Synopsys R&D Manager, HDL Compilers 7. Wikipedia Extensions to Verilog ● Improvements for advanced design requirements – Data types – Higher abstraction (user defined types, struct, unions) – Interfaces ● Properties and assertions built in the language – Assertion Based Verification, Design for Verification ● New features for verification – Models and testbenches using object-oriented techniques (class) – Constrained random test generation – Transaction level modeling ● Direct Programming Interface with C/C++/SystemC – Link to system level simulations Data types: logic module counter (input logic clk, ● Nets and Variables reset, ● enable, Net type,
    [Show full text]
  • COMBINATIONAL CIRCUITS Combinational Plds Basic Configuration of Three Plds (Programmable Logic Devices)
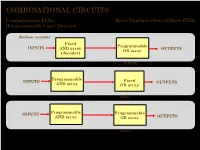
    COMBINATIONAL CIRCUITS Combinational PLDs Basic Configuration of three PLDs (Programmable Logic Devices) Boolean variables Fixed Programmable INPUTS AND array OUTPUTS OR array (decoder) Programmable Read-Only Memory (PROM) Programmable INPUTS Fixed OUTPUTS AND array OR array Programmable Array Logic (PAL) Programmable INPUTS Programmable AND array OR array OUTPUTS (Field) Programmable Logic Array (PLA) 1 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Two-level AND-OR Arrays (Programmable Logic Devices) F (C,B, A) = CBA + CB A A AND B + V B C A C B F C F AND F + V 1 B OR C Multiple functions Simplified equivalent circuit for two-level AND-OR array 2 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Field-programmable AND and OR Arrays (Programmable Logic Devices) Field-programmable logic elements are devices that contain uncommitted AND/OR arrays that are (programmed) configured by the designer. + V + V A A F (C,B, A) F (C,B, A) = CBA B B C C Unprogrammed AND array Fuse can be "blown" by passing a high current through it. 3 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Field-programmable AND and OR Arrays (Programmable Logic Devices) F (P1 ,P2 ,P3 ) = P1 + P3 P1 P1 P2 P2 P3 P3 F F (P1 ,P2 ,P3 ) Unprogrammed OR array Programmed OR array P1 P2 P3 P1 + P3 4 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Output Polarity Options (Programmable Logic Devices) I1 Ik Active high Active low Complementary outputs Programmable polarity P P 1 m + V 5 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs Bidirectional Pins and Feed back Lines (Programmable Logic Devices) I1 Ik Feedback IOm Three-state driver 6 ©Loberg COMBINATIONAL CIRCUITS Combinational PLDs PLA (Programmable Logic Array) (Programmable Logic Devices) If we use ROM to implement the Boolean function we will waste the silicon area.
    [Show full text]
  • Gotcha Again More Subtleties in the Verilog and Systemverilog Standards That Every Engineer Should Know
    Gotcha Again More Subtleties in the Verilog and SystemVerilog Standards That Every Engineer Should Know Stuart Sutherland Sutherland HDL, Inc. [email protected] Don Mills LCDM Engineering [email protected] Chris Spear Synopsys, Inc. [email protected] ABSTRACT The definition of gotcha is: “A misfeature of....a programming language...that tends to breed bugs or mistakes because it is both enticingly easy to invoke and completely unexpected and/or unreasonable in its outcome. A classic gotcha in C is the fact that ‘if (a=b) {code;}’ is syntactically valid and sometimes even correct. It puts the value of b into a and then executes code if a is non-zero. What the programmer probably meant was ‘if (a==b) {code;}’, which executes code if a and b are equal.” (http://www.hyperdictionary.com/computing/gotcha). This paper documents 38 gotchas when using the Verilog and SystemVerilog languages. Some of these gotchas are obvious, and some are very subtle. The goal of this paper is to reveal many of the mysteries of Verilog and SystemVerilog, and help engineers understand the important underlying rules of the Verilog and SystemVerilog languages. The paper is a continuation of a paper entitled “Standard Gotchas: Subtleties in the Verilog and SystemVerilog Standards That Every Engineer Should Know” that was presented at the Boston 2006 SNUG conference [1]. SNUG San Jose 2007 1 More Gotchas in Verilog and SystemVerilog Table of Contents 1.0 Introduction ............................................................................................................................3 2.0 Design modeling gotchas .......................................................................................................4 2.1 Overlapped decision statements ................................................................................... 4 2.2 Inappropriate use of unique case statements ...............................................................
    [Show full text]
  • Synthesis and Verification of Digital Circuits Using Functional Simulation and Boolean Satisfiability
    Synthesis and Verification of Digital Circuits using Functional Simulation and Boolean Satisfiability by Stephen M. Plaza A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy (Computer Science and Engineering) in The University of Michigan 2008 Doctoral Committee: Associate Professor Igor L. Markov, Co-Chair Assistant Professor Valeria M. Bertacco, Co-Chair Professor John P. Hayes Professor Karem A. Sakallah Associate Professor Dennis M. Sylvester Stephen M. Plaza 2008 c All Rights Reserved To my family, friends, and country ii ACKNOWLEDGEMENTS I would like to thank my advisers, Professor Igor Markov and Professor Valeria Bertacco, for inspiring me to consider various fields of research and providing feedback on my projects and papers. I also want to thank my defense committee for their comments and in- sights: Professor John Hayes, Professor Karem Sakallah, and Professor Dennis Sylvester. I would like to thank Professor David Kieras for enhancing my knowledge and apprecia- tion for computer programming and providing invaluable advice. Over the years, I have been fortunate to know and work with several wonderful stu- dents. I have collaborated extensively with Kai-hui Chang and Smita Krishnaswamy and have enjoyed numerous research discussions with them and have benefited from their in- sights. I would like to thank Ian Kountanis and Zaher Andraus for our many fun discus- sions on parallel SAT. I also appreciate the time spent collaborating with Kypros Constan- tinides and Jason Blome. Although I have not formally collaborated with Ilya Wagner, I have enjoyed numerous discussions with him during my doctoral studies. I also thank my office mates Jarrod Roy, Jin Hu, and Hector Garcia.
    [Show full text]
  • A Logic Synthesis Toolbox for Reducing the Multiplicative Complexity in Logic Networks
    A Logic Synthesis Toolbox for Reducing the Multiplicative Complexity in Logic Networks Eleonora Testa∗, Mathias Soekeny, Heinz Riener∗, Luca Amaruz and Giovanni De Micheli∗ ∗Integrated Systems Laboratory, EPFL, Lausanne, Switzerland yMicrosoft, Switzerland zSynopsys Inc., Design Group, Sunnyvale, California, USA Abstract—Logic synthesis is a fundamental step in the real- correlates to the resistance of the function against algebraic ization of modern integrated circuits. It has traditionally been attacks [10], while the multiplicative complexity of a logic employed for the optimization of CMOS-based designs, as well network implementing that function only provides an upper as for emerging technologies and quantum computing. Recently, bound. Consequently, minimizing the multiplicative complexity it found application in minimizing the number of AND gates in of a network is important to assess the real multiplicative cryptography benchmarks represented as xor-and graphs (XAGs). complexity of the function, and therefore its vulnerability. The number of AND gates in an XAG, which is called the logic net- work’s multiplicative complexity, plays a critical role in various Second, the number of AND gates plays an important role cryptography and security protocols such as fully homomorphic in high-level cryptography protocols such as zero-knowledge encryption (FHE) and secure multi-party computation (MPC). protocols, fully homomorphic encryption (FHE), and secure Further, the number of AND gates is also important to assess multi-party computation (MPC) [11], [12], [6]. For example, the the degree of vulnerability of a Boolean function, and influences size of the signature in post-quantum zero-knowledge signatures the cost of techniques to protect against side-channel attacks.
    [Show full text]
  • Development of a Programmable Array Logic
    i DEVELOPMENT OF A PROGRAMMABLE ARRAY LOGIC PROGRAMMER USING A HOME COMPUTER by GERT DANIEL JORDAAN Dissertation submitted in compliance with the requirements for the MASTER'S DIPLOMA in TECHNOLOGY in the Department of Electronics at the TECHNIKON O. F . S . OCTOBER, 1988. Supervisor: Prof. F.W. Bruwer Co-supervisor: Mr. B. de Witt © Central University of Technology, Free State ACKNOWLEDGEMENTS I would like to thank the following persons without whose help this project could hardly have been completed: The supervisor, prof. F.W. Bruwer, and co-supervisor, mr. 8. de Witt, for help and guidance during the course of the project. Mr. H.F. Coetzer for technical as well as philolog ical assistance. It is really appreciated that time could be found in his very full schedule, for this assistance. Dr. C.A.J. van Rensburg for his per_onal interest in the research project and for continuous encouragement and help. Dr. J. van der Mer-we for his assistance - in particular with respect to the registration and other administrative aspects of the project. / Miss M. du Toit who was largely responsible for the word processing. For the guidance provided by my parents and the opportuni- ties which they afforded me. My children, Tania, Johan, Madelie and Lourens,. whose main contribution was to have to forego much of my attention and time for such a long period. Last, but not least, my wife, Christa, for her encouragement and understanding. © Central University of Technology,ii Free State CONTENTS PAGE Cilapter 1 1 Intr--oduc tion 1.1 Recent Trends in Electronics 1 1.2 Problem Investigated 1 1.3 Development of PAL Programmer 3 1.3.1 Generation of Fuse Map 3 1.3.2 Programming of Programmable Array Logic 3 Devices 1 .
    [Show full text]
  • Logic Optimization and Synthesis: Trends and Directions in Industry
    Logic Optimization and Synthesis: Trends and Directions in Industry Luca Amaru´∗, Patrick Vuillod†, Jiong Luo∗, Janet Olson∗ ∗ Synopsys Inc., Design Group, Sunnyvale, California, USA † Synopsys Inc., Design Group, Grenoble, France Abstract—Logic synthesis is a key design step which optimizes of specific logic styles and cell layouts. Embedding as much abstract circuit representations and links them to technology. technology information as possible early in the logic optimiza- With CMOS technology moving into the deep nanometer regime, tion engine is key to make advantageous logic restructuring logic synthesis needs to be aware of physical informations early in the flow. With the rise of enhanced functionality nanodevices, opportunities carry over at the end of the design flow. research on technology needs the help of logic synthesis to capture In this paper, we examine the synergy between logic synthe- advantageous design opportunities. This paper deals with the syn- sis and technology, from an industrial perspective. We present ergy between logic synthesis and technology, from an industrial technology aware synthesis methods incorporating advanced perspective. First, we present new synthesis techniques which physical information at the core optimization engine. Internal embed detailed physical informations at the core optimization engine. Experiments show improved Quality of Results (QoR) and results evidence faster timing closure and better correlation better correlation between RTL synthesis and physical implemen- between RTL synthesis and physical implementation. We elab- tation. Second, we discuss the application of these new synthesis orate on synthesis aware technology development, where logic techniques in the early assessment of emerging nanodevices with synthesis enables a fair system-level assessment on emerging enhanced functionality.
    [Show full text]
  • Yikes! Why Is My Systemverilog Still So Slooooow?
    DVCon-2019 San Jose, CA Voted Best Paper 1st Place World Class SystemVerilog & UVM Training Yikes! Why is My SystemVerilog Still So Slooooow? Cliff Cummings John Rose Adam Sherer Sunburst Design, Inc. Cadence Design Systems, Inc. Cadence Design System, Inc. [email protected] [email protected] [email protected] www.sunburst-design.com www.cadence.com www.cadence.com ABSTRACT This paper describes a few notable SystemVerilog coding styles and their impact on simulation performance. Benchmarks were run using the three major SystemVerilog simulation tools and those benchmarks are reported in the paper. Some of the most important coding styles discussed in this paper include UVM string processing and SystemVerilog randomization constraints. Some coding styles showed little or no impact on performance for some tools while the same coding styles showed large simulation performance impact. This paper is an update to a paper originally presented by Adam Sherer and his co-authors at DVCon in 2012. The benchmarking described in this paper is only for coding styles and not for performance differences between vendor tools. DVCon 2019 Table of Contents I. Introduction 4 Benchmarking Different Coding Styles 4 II. UVM is Software 5 III. SystemVerilog Semantics Support Syntax Skills 10 IV. Memory and Garbage Collection – Neither are Free 12 V. It is Best to Leave Sleeping Processes to Lie 14 VI. UVM Best Practices 17 VII. Verification Best Practices 21 VIII. Acknowledgment 25 References 25 Author & Contact Information 25 Page 2 Yikes! Why is
    [Show full text]
  • Designing a RISC CPU in Reversible Logic
    Designing a RISC CPU in Reversible Logic Robert Wille Mathias Soeken Daniel Große Eleonora Schonborn¨ Rolf Drechsler Institute of Computer Science, University of Bremen, 28359 Bremen, Germany frwille,msoeken,grosse,eleonora,[email protected] Abstract—Driven by its promising applications, reversible logic In this paper, the recent progress in the field of reversible cir- received significant attention. As a result, an impressive progress cuit design is employed in order to design a complex system, has been made in the development of synthesis approaches, i.e. a RISC CPU composed of reversible gates. Starting from implementation of sequential elements, and hardware description languages. In this paper, these recent achievements are employed a textual specification, first the core components of the CPU in order to design a RISC CPU in reversible logic that can are identified. Previously introduced approaches are applied execute software programs written in an assembler language. The next to realize the respective combinational and sequential respective combinational and sequential components are designed elements. More precisely, the combinational components are using state-of-the-art design techniques. designed using the reversible hardware description language SyReC [17], whereas for the realization of the sequential I. INTRODUCTION elements an external controller (as suggested in [16]) is utilized. With increasing miniaturization of integrated circuits, the Plugging the respective components together, a CPU design reduction of power dissipation has become a crucial issue in results which can process software programs written in an today’s hardware design process. While due to high integration assembler language. This is demonstrated in a case study, density and new fabrication processes, energy loss has sig- where the execution of a program determining Fibonacci nificantly been reduced over the last decades, physical limits numbers is simulated.
    [Show full text]
  • A Syntax Rule Summary
    A Syntax Rule Summary Below we present the syntax of PSL in Backus-Naur Form (BNF). A.1 Conventions The formal syntax described uses the following extended Backus-Naur Form (BNF). a. The initial character of each word in a nonterminal is capitalized. For ex- ample: PSL Statement A nonterminal is either a single word or multiple words separated by underscores. When a multiple word nonterminal containing underscores is referenced within the text (e.g., in a statement that describes the se- mantics of the corresponding syntax), the underscores are replaced with spaces. b. Boldface words are used to denote reserved keywords, operators, and punc- tuation marks as a required part of the syntax. For example: vunit ( ; c. The ::= operator separates the two parts of a BNF syntax definition. The syntax category appears to the left of this operator and the syntax de- scription appears to the right of the operator. For example, item (d) shows three options for a Vunit Type. d. A vertical bar separates alternative items (use one only) unless it appears in boldface, in which case it stands for itself. For example: From IEEE Std.1850-2005. Copyright 2005 IEEE. All rights reserved.* 176 Appendix A. Syntax Rule Summary Vunit Type ::= vunit | vprop | vmode e. Square brackets enclose optional items unless it appears in boldface, in which case it stands for itself. For example: Sequence Declaration ::= sequence Name [ ( Formal Parameter List ) ]DEFSYM Sequence ; indicates that ( Formal Parameter List ) is an optional syntax item for Sequence Declaration,whereas | Sequence [*[ Range ] ] indicates that (the outer) square brackets are part of the syntax, while Range is optional.
    [Show full text]
  • Logic Synthesis Meets Machine Learning: Trading Exactness for Generalization
    Logic Synthesis Meets Machine Learning: Trading Exactness for Generalization Shubham Raif,6,y, Walter Lau Neton,10,y, Yukio Miyasakao,1, Xinpei Zhanga,1, Mingfei Yua,1, Qingyang Yia,1, Masahiro Fujitaa,1, Guilherme B. Manskeb,2, Matheus F. Pontesb,2, Leomar S. da Rosa Juniorb,2, Marilton S. de Aguiarb,2, Paulo F. Butzene,2, Po-Chun Chienc,3, Yu-Shan Huangc,3, Hoa-Ren Wangc,3, Jie-Hong R. Jiangc,3, Jiaqi Gud,4, Zheng Zhaod,4, Zixuan Jiangd,4, David Z. Pand,4, Brunno A. de Abreue,5,9, Isac de Souza Camposm,5,9, Augusto Berndtm,5,9, Cristina Meinhardtm,5,9, Jonata T. Carvalhom,5,9, Mateus Grellertm,5,9, Sergio Bampie,5, Aditya Lohanaf,6, Akash Kumarf,6, Wei Zengj,7, Azadeh Davoodij,7, Rasit O. Topalogluk,7, Yuan Zhoul,8, Jordan Dotzell,8, Yichi Zhangl,8, Hanyu Wangl,8, Zhiru Zhangl,8, Valerio Tenacen,10, Pierre-Emmanuel Gaillardonn,10, Alan Mishchenkoo,y, and Satrajit Chatterjeep,y aUniversity of Tokyo, Japan, bUniversidade Federal de Pelotas, Brazil, cNational Taiwan University, Taiwan, dUniversity of Texas at Austin, USA, eUniversidade Federal do Rio Grande do Sul, Brazil, fTechnische Universitaet Dresden, Germany, jUniversity of Wisconsin–Madison, USA, kIBM, USA, lCornell University, USA, mUniversidade Federal de Santa Catarina, Brazil, nUniversity of Utah, USA, oUC Berkeley, USA, pGoogle AI, USA The alphabetic characters in the superscript represent the affiliations while the digits represent the team numbers yEqual contribution. Email: [email protected], [email protected], [email protected], [email protected] Abstract—Logic synthesis is a fundamental step in hard- artificial intelligence.
    [Show full text]
  • JTAG Simulation VIP Datasheet
    VIP Datasheet Simulation VIP for JTAG Provides JTAG and cJTAG support Overview Cadence® Simulation VIP is the world’s most widely used VIP for digital simulation. Hundreds of customers have used Cadence VIP to verify thousands of designs, from IP blocks to full systems on chip (SoCs). The Simulation VIP is ready-made for your environment, providing consistent results whether you are using Cadence Incisive®, Synopsys VCS®, or Mentor Questa® simulators. You have the freedom to build your testbench using any of these verification languages: SystemVerilog, e, Verilog, VHDL, or C/C++. Cadence Simulation VIP supports the Universal Verification Methodology (UVM) as well as legacy methodologies. The unique flexible architecture of Cadence VIP makes this possible. It includes a multi-language testbench interface with full access to the source code to make it easy to integrate VIP with your testbench. Optimized cores for simulation and simulation-acceleration allow you to choose the verification approach that best meets your objectives. Deliverables Specification Support People sometimes think of VIP as just a bus functional model The JTAG VIP supports the JTAG Protocol v1.c from 2001 as (BFM) that responds to interface traffic. But SoC verification defined in the JTAG Protocol Specification. requires much more than just a BFM. Cadence Simulation VIP components deliver: • State machine models incorporate the subtle features of Supported Design-Under-Test Configurations state machine behavior, such as support for multi-tiered, Master Slave Hub/Switch power-saving modes Full Stack Controller-only PHY-only • Pre-programmed assertions that are built into the VIP to continuously watch simulation traffic to check for protocol violations.
    [Show full text]