Dissipative Dark Matter Explains Rotation Curves
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Search For" Dwarf" Seyfert Nuclei. VII. a Catalog of Central Stellar
TO APPEAR IN The Astrophysical Journal Supplement Series. Preprint typeset using LATEX style emulateapj v. 26/01/00 A SEARCH FOR “DWARF” SEYFERT NUCLEI. VII. A CATALOG OF CENTRAL STELLAR VELOCITY DISPERSIONS OF NEARBY GALAXIES LUIS C. HO The Observatories of the Carnegie Institution of Washington, 813 Santa Barbara St., Pasadena, CA 91101 JENNY E. GREENE1 Department of Astrophysical Sciences, Princeton University, Princeton, NJ ALEXEI V. FILIPPENKO Department of Astronomy, University of California, Berkeley, CA 94720-3411 AND WALLACE L. W. SARGENT Palomar Observatory, California Institute of Technology, MS 105-24, Pasadena, CA 91125 To appear in The Astrophysical Journal Supplement Series. ABSTRACT We present new central stellar velocity dispersion measurements for 428 galaxies in the Palomar spectroscopic survey of bright, northern galaxies. Of these, 142 have no previously published measurements, most being rela- −1 tively late-type systems with low velocity dispersions (∼<100kms ). We provide updates to a number of literature dispersions with large uncertainties. Our measurements are based on a direct pixel-fitting technique that can ac- commodate composite stellar populations by calculating an optimal linear combination of input stellar templates. The original Palomar survey data were taken under conditions that are not ideally suited for deriving stellar veloc- ity dispersions for galaxies with a wide range of Hubble types. We describe an effective strategy to circumvent this complication and demonstrate that we can still obtain reliable velocity dispersions for this sample of well-studied nearby galaxies. Subject headings: galaxies: active — galaxies: kinematics and dynamics — galaxies: nuclei — galaxies: Seyfert — galaxies: starburst — surveys 1. INTRODUCTION tors, apertures, observing strategies, and analysis techniques. -
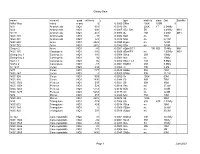
Galaxy Data Name Constell
Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell. -

190 Index of Names
Index of names Ancora Leonis 389 NGC 3664, Arp 005 Andriscus Centauri 879 IC 3290 Anemodes Ceti 85 NGC 0864 Name CMG Identification Angelica Canum Venaticorum 659 NGC 5377 Accola Leonis 367 NGC 3489 Angulatus Ursae Majoris 247 NGC 2654 Acer Leonis 411 NGC 3832 Angulosus Virginis 450 NGC 4123, Mrk 1466 Acritobrachius Camelopardalis 833 IC 0356, Arp 213 Angusticlavia Ceti 102 NGC 1032 Actenista Apodis 891 IC 4633 Anomalus Piscis 804 NGC 7603, Arp 092, Mrk 0530 Actuosus Arietis 95 NGC 0972 Ansatus Antliae 303 NGC 3084 Aculeatus Canum Venaticorum 460 NGC 4183 Antarctica Mensae 865 IC 2051 Aculeus Piscium 9 NGC 0100 Antenna Australis Corvi 437 NGC 4039, Caldwell 61, Antennae, Arp 244 Acutifolium Canum Venaticorum 650 NGC 5297 Antenna Borealis Corvi 436 NGC 4038, Caldwell 60, Antennae, Arp 244 Adelus Ursae Majoris 668 NGC 5473 Anthemodes Cassiopeiae 34 NGC 0278 Adversus Comae Berenices 484 NGC 4298 Anticampe Centauri 550 NGC 4622 Aeluropus Lyncis 231 NGC 2445, Arp 143 Antirrhopus Virginis 532 NGC 4550 Aeola Canum Venaticorum 469 NGC 4220 Anulifera Carinae 226 NGC 2381 Aequanimus Draconis 705 NGC 5905 Anulus Grahamianus Volantis 955 ESO 034-IG011, AM0644-741, Graham's Ring Aequilibrata Eridani 122 NGC 1172 Aphenges Virginis 654 NGC 5334, IC 4338 Affinis Canum Venaticorum 449 NGC 4111 Apostrophus Fornac 159 NGC 1406 Agiton Aquarii 812 NGC 7721 Aquilops Gruis 911 IC 5267 Aglaea Comae Berenices 489 NGC 4314 Araneosus Camelopardalis 223 NGC 2336 Agrius Virginis 975 MCG -01-30-033, Arp 248, Wild's Triplet Aratrum Leonis 323 NGC 3239, Arp 263 Ahenea -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S
Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S. Mcgaugh To cite this version: Benoit Famaey, Stacy S. Mcgaugh. Modified Newtonian Dynamics (MOND): Observational Phe- nomenology and Relativistic Extensions. Living Reviews in Relativity, 2012, 15 (1), 10.12942/lrr- 2012-10. hal-02927744 HAL Id: hal-02927744 https://hal.archives-ouvertes.fr/hal-02927744 Submitted on 1 Sep 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Living Rev. Relativity, 15, (2012), 10 LIVINGREVIEWS http://www.livingreviews.org/lrr-2012-10 in relativity Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Beno^ıtFamaey Observatoire Astronomique de Strasbourg CNRS, UMR 7550, France and AIfA, University of Bonn, Germany email: [email protected] http://astro.u-strasbg.fr/~famaey/ Stacy S. McGaugh Department of Astronomy University of Maryland, USA and Case Western Reserve University, USA email: [email protected] http://astroweb.case.edu/ssm/ Accepted on 30 April 2012 Published on 7 September 2012 Abstract A wealth of astronomical data indicate the presence of mass discrepancies in the Universe. The motions observed in a variety of classes of extragalactic systems exceed what can be explained by the mass visible in stars and gas. -

The Distribution of Dark and Luminous Matter Inferred from Extended
Mon. Not. R. Astron. Soc. 000, 1 – 28 (2015) Printed 27 January 2015 (MN LATEX style file v2.2) The distribution of dark and luminous matter inferred from extended rotation curves. Roelof Bottema1 and Jos´eLuis G. Pesta˜na2 1Kapteyn Astronomical Institute, PO Box 800, NL-9700 AV Groningen, The Netherlands, [email protected] 2Departamento de F´ısica, Universidad de Ja´en, Campus Las Lagunillas, 23071 Ja´en, Spain, [email protected] Accepted: date1. Received: in original form: ABSTRACT A better understanding of the formation of mass structures in the universe can be obtained by determining the amount and distribution of dark and luminous matter in spiral galaxies. To investigate such matters a sample of 12 galaxies, most with accurate distances, has been composed of which the luminosities are distributed regularly over 1 a range spanning 2 2 orders of magnitude. Of the observed high quality and extended rotation curves of these galaxies decompositions have been made, for four different schemes, each with two free parameters. For a “maximum disc fit” the rotation curves can be well matched, yet a large range of mass-to-light ratios for the individual galax- ies is required. For the alternative gravitational theory of MOND the rotation curves can be explained if the fundamental parameter associated with MOND is allowed as a free parameter. Fixing that parameter leads to a disagreement between the predicted and observed rotation curves for a few galaxies. When cosmologically motivated NFW dark matter halos are assumed, the rotation curves for the least massive galaxies can, by no means, be reproduced; cores are definitively preferred over cusps. -

Arxiv:0704.2705V1
Accepted in AJ (for August 2007 issue) Chemical Properties of Star Forming Dwarf Galaxies Ovidiu Vaduvescu1 Instituto de Astronom´ıa, Universidad Cat´olica del Norte Avenida Angamos 0610, Antofagasta, Chile Former address: ACRU & SAAO, University of KwaZulu-Natal, School of Mathematical Sciences, Durban 4041, South Africa Marshall L. McCall2 York University, Department of Physics and Astronomy 4700 Keele Street, M3J 1P3, Toronto, ON, Canada Michael G. Richer3 Observatorio Astr´onomico Nacional, Instituto de Astronomia Universidad Nacional Aut´onoma de M´exico PO Box 439027, San Diego, CA 92143-9027, USA ABSTRACT Recent studies of the near-infrared (NIR) properties of dwarf irregular galaxies (dIs) and blue compact dwarfs (BCDs) have provided improved estimates for the NIR luminosity of old stellar populations in these galaxies. These can be used to derive gas fractions, and thereby to evaluate how BCDs have evolved with respect arXiv:0704.2705v1 [astro-ph] 20 Apr 2007 to dIs. Oxygen abundances have been derived for four BCDs in the Virgo Cluster from a run at Gemini-North in 2003. Combining these new abundances with published values, we study the correlations among the metallicity, Ks luminosity, gas mass, baryonic mass, and gas fraction. Within errors, the two types of dwarfs appear to share a common relation between the oxygen abundance and the luminosity in Ks. The correlation between metallicity and the gas fraction 1email: [email protected] 2email: [email protected] 3email: [email protected] –2– is the same for BCDs as for dIs, indicating that BCD evolution has been similar to dIs. Since dIs appear to have evolved as isolated systems, the BCD bursts are unlikely to be a consequence of gas infall or merging. -

Revised Photometric Distances to Nearby Dwarf Galaxies in the IC 342/Maffei Complex
SUPPLEMENT SERIES Astron. Astrophys. Suppl. Ser. 124, 559-571 (1997) Revised photometric distances to nearby dwarf galaxies in the IC 342/Maffei complex I. Karachentsev1, I. Drozdovsky2,S.Kajsin1,L.O.Takalo3,P.Hein¨am¨aki3, and M. Valtonen3 1 Special Astrophysical Observatory, N.Arkhyz, Stavropolski Kraj 357147, Russia 2 Astronomical Institute, St.-Petersburg State University, Petrodvoretz 198904, Russia 3 Tuorla Observatory, Turku, Finland Received November 12; accepted December 16, 1996 Abstract. The results of DAOPHOT photometry of sev- (B¨orngen & Karachentseva 1985) and also with POSS- eral hundred stars in five irregular galaxies are presented II films (Karachentseva & Karachentsev 1997) have re- using V and I CCD frames, obtained with the Nordic vealed some other candidates to be probable members Optical Telescope under a 0.6 arcsec seeing. Based on the of this nearby complex of galaxies. The distribution of brightest blue and red stars we estimate the following dis- the galaxies is presented in Fig. 1 in galactic coordinates. tances to the galaxies: 3.2 Mpc for UGCA 105, 2.6 Mpc for The galaxies with corrected radial velocities V0 below UGCA 86, 1.8 Mpc for UGCA 92, 1.7 Mpc for NGC 1569, 500 km/s are indicated with open circles, and other pos- and 1.7 Mpc for Cas 1. The problem of membership of the sible new members of the complex are noted with crosses. 1 galaxies to the IC 342/Maffei complex is briefly discussed . Except for Maffei 1, Dwingeloo 1, Dwingeloo 2, and MB 1, situated in the strongest absorption zone, the Key words: galaxies: irregular — galaxies: distances — rest of the galaxies with V0 < 500 km/shavealready galaxies: stellar content been resolved into stars. -

The Stellar Halo of the Spiral Galaxy NGC 1560
The Astrophysical Journal, 861:81 (7pp), 2018 July 10 https://doi.org/10.3847/1538-4357/aac821 © 2018. The American Astronomical Society. All rights reserved. The Stellar Halo of the Spiral Galaxy NGC 1560 Laura Greggio1 , Renato Falomo1 , and Riccardo Scarpa2,3 1 INAF, Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5 I-35122 Padova, Italy; [email protected] 2 Instituto de Astrofisica de Canarias, C/O Via Lactea, s/n E38205, La Laguna (Tenerife), Spain 3 Universidad de La Laguna, Dpto. Astrofsica, s/n E-38206 La Laguna (Tenerife), Spain Received 2018 March 23; revised 2018 May 15; accepted 2018 May 23; published 2018 July 6 Abstract 9 We report on the detection of a stellar halo around NGC 1560, a 10 Me spiral galaxy member of the Maffei group. We obtained deep images in the r- and i-bands using the 10.4 m Gran Telescopio Canarias in a field centered at ∼3.7 arcmin (projected distance of 3.5 kpc) from the center of this galaxy. The luminosity function and the color– magnitude diagram show a clear excess of stars with respect to the expected foreground level at magnitudes fainter than the red giant branch tip at the distance of NGC 1560. The colors of the halo stars imply a metallicity of 7 Z∼Ze/50, while their counts correspond to a stellar mass of ∼10 Me in the sampled region. Assuming a power- 8 law profile for the surface mass density of the halo, our data suggest a total stellar mass of 10 Me for the halo of NGC 1560. -

A ROSAT HRI Survey of Bright Nearby Galaxies 3
Mon. Not. R. Astron. Soc. 000, 000–000 (0000) Printed 30 October 2018 (MN LATEX style file v1.4) A ROSAT HRI survey of bright nearby galaxies T.P. Roberts and R.S. Warwick Department of Physics and Astronomy, University of Leicester, University Road, Leicester, LE1 7RH ABSTRACT We use the extensive public archive of ROSAT High Resolution Imager (HRI) observations to carry out a statistical investigation of the X-ray properties of nearby galaxies. Specifically we focus on the sample of 486 bright (BT ≤ 12.5) northern galax- ies studied by Ho, Filippenko and Sargent (HFS) in the context of their exploration of the optical spectroscopic properties of nearby galactic nuclei. Over 20% of HFS galaxies are encompassed in ROSAT HRI fields of reasonable (≥ 10ks) exposure. The X-ray sources detected within the optical extent of each galaxy are categorised as either nuclear or non-nuclear depending on whether the source is positioned within or outside of a 25′′ radius circle centred on the optical nucleus. A nuclear X-ray source is detected in over 70% of the galaxies harbouring either a Seyfert or LINER nucleus compared to a detection rate of only ∼ 40% in less active systems. The correlation of the Hα luminosity with nuclear X-ray luminosity previ- ously observed in QSOs and bright Seyfert 1 galaxies appears to extend down into the 38 40 −1 regime of ultra-low luminosity (LX∼ 10 −10 erg s ) active galactic nuclei (AGN). The inferred accretion rates for this sample of low-luminosity AGN are significantly sub-Eddington. In total 142 non-nuclear sources were detected. -

Andromeda - Daughter of Cassiopeia
May 18 2021 Andromeda - Daughter of Cassiopeia Observed: No Object Her Type Mag Alias/Notes IC 5372 Non-Existent IC 1530 Non-Existent NGC 19 Non-Existent NGC 44 Non-Existent NGC 6 Non-Existent NGC 67A Non-Existent IC 1539 Non-Existent NGC 70 NGC 82 Non-Existent NGC 85B Non-Existent NGC 537 Non-Existent IC 1665 Non-Existent Single Star NGC 317 Non-Existent IC 1580 Non-Existent Single Star NGC 162 Non-Existent STAR IC 24 Non-Existent Single Star NGC 90 Non-Existent IC 1547 Non-Existent NGC 85A Non-Existent IC 240 Non-Existent NGC 999 NGC 846 Non-Existent NGC 847 IC 1737 Non-Existent IC 1707 Non-Existent IC 1545 Non-Existent IC 1538 Non-Existent Sub Total: 24 Observed: Yes Object Her Type Mag Alias/Notes C 410 Nebula 16 Cluster+Nebula in M31 Close to G280 G 87 Globular 15.6 IC 1541 Glxy 15.5 CGCG 478-55 PGC 1287 IC 1540 Glxy SBb 14.9 UGC 186 MCG 4-1-50 CGCG 478-54 PGC 1276 IC 1536 Glxy E/S0 15.4 MCG 8-1-32 MK 939 CGCG 549-28 PGC 949 IC 1535 Glxy S 15.1 UGC 131 MCG 8-1-30 CGCG 549-26 PGC 922 IC 1534 Glxy S0 14.8 UGC 125 MCG 8-1-28 CGCG 549-25 5ZW6 PGC 910 IC 1525 Glxy SBb 13 UGC 12883 MCG 8-1-16 CGCG 548-20 CGCG 549-11 IRAS 23567+4636 PGC 73150 IC 239 Glxy SAB(rs)cd 11.8 UGC 2080 MCG 6-6-65 CGCG 523-71 IRAS 2333+3845 PGC 9899 IC 179 Glxy E 13.6 UGC 1475 MCG 6-5-75 CGCG 522-101 PGC 7581 IC 178 Glxy Sab 14.1 UGC 1456 MCG 6-5-70 CGCG 522-94 IRAS 1559+3625 PGC 7488 IC 65 Glxy SAB(s)bc 13.6 UGC 625 MCG 8-3-5 CGCG 551-4 IRAS 580+4724 PGC 3635 IC 46 Glxy S0? 14.8 CGCG 479-63 KARA32 PGC 2575 IC 45 Glxy Pec 15.4 UGC 449 MCG 5-2-39 CGCG 500-73 PGC 2537