DOCSLIB.ORG

Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Living Rev. Relativity, 15, (2012), 10 LIVINGREVIEWS http://www.livingreviews.org/lrr-2012-10 in relativity Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Beno^ıtFamaey Observatoire Astronomique de Strasbourg CNRS, UMR 7550, France and AIfA, University of Bonn, Germany email: [email protected] http://astro.u-strasbg.fr/~famaey/ Stacy S. McGaugh Department of Astronomy University of Maryland, USA and Case Western Reserve University, USA email: [email protected] http://astroweb.case.edu/ssm/ Accepted on 30 April 2012 Published on 7 September 2012 Abstract A wealth of astronomical data indicate the presence of mass discrepancies in the Universe. The motions observed in a variety of classes of extragalactic systems exceed what can be explained by the mass visible in stars and gas. Either (i) there is a vast amount of unseen mass in some novel form { dark matter { or (ii) the data indicate a breakdown of our understanding of dynamics on the relevant scales, or (iii) both. Here, we first review a few outstanding challenges for the dark matter interpretation of mass discrepancies in galaxies, purely based on observations and independently of any alternative theoretical framework. We then show that many of these puzzling observations are predicted by one single relation { Milgrom's law { involving an acceleration constant a0 (or a characteristic surface density Σy = a0=G) on the order of the square-root of the cosmological constant in natural units. This relation can at present most easily be interpreted as the effect of a single universal force law resulting froma modification of Newtonian dynamics (MOND) on galactic scales. We exhaustively reviewthe current observational successes and problems of this alternative paradigm at all astrophysical scales, and summarize the various theoretical attempts (TeVeS, GEA, BIMOND, and others) made to effectively embed this modification of Newtonian dynamics within a relativistic theory of gravity. This review is licensed under a Creative Commons Attribution-Non-Commercial-NoDerivs 3.0 Germany License. http://creativecommons.org/licenses/by-nc-nd/3.0/de/ Imprint / Terms of Use Living Reviews in Relativity is a peer reviewed open access journal published by the Max Planck Institute for Gravitational Physics, Am M¨uhlenberg 1, 14476 Potsdam, Germany. ISSN 1433-8351. This review is licensed under a Creative Commons Attribution-Non-Commercial-NoDerivs 3.0 Germany License: http://creativecommons.org/licenses/by-nc-nd/3.0/de/. Figures that have been previously published elsewhere may not be reproduced without consent of the original copyright holders. Because a Living Reviews article can evolve over time, we recommend to cite the article as follows: Beno^ıtFamaey and Stacy S. McGaugh, \Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions", Living Rev. Relativity, 15, (2012), 10. [Online Article]: cited [<date>], http://www.livingreviews.org/lrr-2012-10 The date given as <date> then uniquely identifies the version of the article you are referring to. Article Revisions Living Reviews supports two ways of keeping its articles up-to-date: Fast-track revision A fast-track revision provides the author with the opportunity to add short notices of current research results, trends and developments, or important publications to the article. A fast-track revision is refereed by the responsible subject editor. If an article has undergone a fast-track revision, a summary of changes will be listed here. Major update A major update will include substantial changes and additions and is subject to full external refereeing. It is published with a new publication number. For detailed documentation of an article's evolution, please refer to the history document of the article's online version at http://www.livingreviews.org/lrr-2012-10. Contents 1 Introduction 5 2 The Missing Mass Problem in a Nutshell7 3 A Brief Overview of the ΛCDM Cosmological Model 11 3.1 Dark Energy (Λ)..................................... 11 3.2 Cold Dark Matter (CDM)................................ 12 4 Some Challenges for the ΛCDM Model 13 4.1 Coincidences....................................... 13 4.2 Unobserved predictions................................. 14 4.3 Unpredicted observations................................ 18 4.3.1 Baryonic Tully{Fisher relation......................... 18 4.3.2 The role of surface density............................ 24 4.3.3 Mass discrepancy-acceleration relation..................... 27 4.3.4 Renzo's rule.................................... 31 5 Milgrom's Empirical Law and \Kepler Laws" of Galactic Dynamics 35 5.1 Milgrom's law and the dielectric analogy........................ 35 5.2 Galactic Kepler-like laws of motion........................... 37 6 Milgrom's Law as a Modification of Classical Dynamics: MOND 42 6.1 Modified inertia or modified gravity: Non-relativistic actions............ 42 6.1.1 Modified inertia................................. 43 6.1.2 Bekenstein{Milgrom MOND.......................... 44 6.1.3 QUMOND.................................... 46 6.2 The interpolating function................................ 50 6.3 The external field effect................................. 54 6.4 MOND in the solar system............................... 56 6.5 MOND in rotationally-supported stellar systems................... 57 6.5.1 Rotation curves of disk galaxies......................... 57 6.5.2 The Milky Way.................................. 67 6.5.3 Disk stability and interacting galaxies..................... 69 6.5.4 Tidal dwarf galaxies............................... 73 6.6 MOND in pressure-supported stellar systems..................... 75 6.6.1 Elliptical galaxies................................. 75 6.6.2 Dwarf spheroidal galaxies............................ 78 6.6.3 Star clusters................................... 80 6.6.4 Galaxy groups and clusters........................... 81 7 Relativistic MOND Theories 87 7.1 Scalar-tensor k-essence.................................. 88 7.2 Stratified theory..................................... 90 7.3 Original Tensor-Vector-Scalar theory.......................... 90 7.4 Generalized Tensor-Vector-Scalar theory........................ 91 7.5 Bi-Scalar-Tensor-Vector theory............................. 92 7.6 Non-minimal scalar-tensor formalism.......................... 92 7.7 Generalized Einstein-Aether theories.......................... 93 7.8 Bimetric theories..................................... 95 7.9 Dipolar dark matter................................... 96 7.10 Non-local theories and other ideas........................... 97 8 Gravitational Lensing in Relativistic MOND 100 8.1 Strong lensing by galaxies................................ 100 8.2 Weak lensing by galaxies................................. 103 8.3 Strong and weak lensing by galaxy clusters...................... 103 8.4 Weak lensing by large-scale structure.......................... 107 9 MOND and Cosmology 108 9.1 Expansion history.................................... 108 9.2 Large-scale structure and Cosmic Microwave Background.............. 109 10 Summary and Discussion 117 11 Acknowledgements 126 References 127 List of Tables 1 Values predicted from the Besan¸conmodel of the Milky Way in MOND as seen by a Newtonist........................................ 69 2 Observational tests of MOND.............................. 125 Modified Newtonian Dynamics (MOND) 5 1 Introduction Two of the most tantalizing mysteries of modern astrophysics are known as the dark matter and dark energy problems. These problems come from the discrepancies between, on one side, the observations of galactic and extragalactic systems (as well as the observable Universe itself in the case of dark energy) by astronomical means, and on the other side, the predictions of general relativity from the observed amount of matter-energy in these systems. In short, what astronomical observations are telling us is that the dynamics of galactic and extragalactic systems, as well as the expansion of the Universe itself, do not correspond to the observed mass-energy as they should if our understanding of gravity is complete. Thus, this indicates either (i) the presence of unseen (and yet unknown) mass-energy, or (ii) a failure of our theory of gravity, or (iii) both. The third case is a priori the most plausible, as there are good reasons for there being more particles than those of the standard model of particle physics [257] (actually, even in the case of baryons, we suspect that a lot of them have not yet been seen and, thus, literally make up unseen mass, in the form of \missing baryons"), and as there is a priori no reason that general relativity should be valid over a wide range of scales, where it has never been tested [45], and where the need for a dark sector actually prevents the theory from being tested until this sector has been detected by other means than gravity itself1. However, either of the first two cases could be the dominant explanation of the discrepancies in a given class of astronomical systems (or even in all astronomical systems), and this is actually testable. For instance, as far as (ii) is concerned, if the mass discrepancies in a class of systems are mostly caused by some subtle change in gravitational physics, then there should be a clear signature of a single, universal force law at work in this whole class of systems. If instead there is a distinct dark matter component in these, the kinematics of any given system should
Load more

Recommended publications
  • Publications of the Astronomical Society of the Pacific Vol. 109 1997
    Publications of the Astronomical Society of the Pacific Vol. 109 1997 July No. 737 Publications of the Astronomical Society of the Pacific 109: 745-758, 1997 July Invited Review Paper Low-Surface-Brightness Galaxies: Hidden Galaxies Revealed Greg Bothun Department of Physics, University of Oregon, Eugene, Oregon 97403 Electronic mail: [email protected] Chris Impey Steward Observatory, University of Arizona, Tucson, Arizona 85721 Electronic mail: [email protected] Stacy McGaugh Department of Terrestrial Magnetism, Carnegie Institution of Washington, DC 20005 Electronic mail: [email protected] Received 1997 February 12; accepted 1997 April 29 ABSTRACT. In 20 years, low-surface-brightness (LSB) galaxies have evolved from being an idiosyncratic notion to being one of the major baryonic repositories in the Universe. The story of their discovery and the characterization of their properties is told here. Their recovery from the noise of the night-sky background is a strong testament to the severity of surface-brightness selection effects. LSB galaxies have a number of remarkable properties which distinguish them from the more familiar Hubble sequence of spirals. The two most important are (1) they evolve at a significantly slower rate and may well experience star formation outside of the molecular-cloud environment, (2) they are embedded in dark-matter halos which are of lower density and more extended than the halos around high-surface-brightness (HSB) disk galaxies. Compared to HSB disks, LSB disks are strongly dark-matter dominated at all radii and show a systematic increase in M/L with decreasing central surface brightness. In addition, the recognition that large numbers of LSB galaxies actually exist has changed the form of the galaxy luminosity function and has clearly increased the space density of galaxies at ζ = 0.
    [Show full text]
  • A Search For" Dwarf" Seyfert Nuclei. VII. a Catalog of Central Stellar
    TO APPEAR IN The Astrophysical Journal Supplement Series. Preprint typeset using LATEX style emulateapj v. 26/01/00 A SEARCH FOR “DWARF” SEYFERT NUCLEI. VII. A CATALOG OF CENTRAL STELLAR VELOCITY DISPERSIONS OF NEARBY GALAXIES LUIS C. HO The Observatories of the Carnegie Institution of Washington, 813 Santa Barbara St., Pasadena, CA 91101 JENNY E. GREENE1 Department of Astrophysical Sciences, Princeton University, Princeton, NJ ALEXEI V. FILIPPENKO Department of Astronomy, University of California, Berkeley, CA 94720-3411 AND WALLACE L. W. SARGENT Palomar Observatory, California Institute of Technology, MS 105-24, Pasadena, CA 91125 To appear in The Astrophysical Journal Supplement Series. ABSTRACT We present new central stellar velocity dispersion measurements for 428 galaxies in the Palomar spectroscopic survey of bright, northern galaxies. Of these, 142 have no previously published measurements, most being rela- −1 tively late-type systems with low velocity dispersions (∼<100kms ). We provide updates to a number of literature dispersions with large uncertainties. Our measurements are based on a direct pixel-fitting technique that can ac- commodate composite stellar populations by calculating an optimal linear combination of input stellar templates. The original Palomar survey data were taken under conditions that are not ideally suited for deriving stellar veloc- ity dispersions for galaxies with a wide range of Hubble types. We describe an effective strategy to circumvent this complication and demonstrate that we can still obtain reliable velocity dispersions for this sample of well-studied nearby galaxies. Subject headings: galaxies: active — galaxies: kinematics and dynamics — galaxies: nuclei — galaxies: Seyfert — galaxies: starburst — surveys 1. INTRODUCTION tors, apertures, observing strategies, and analysis techniques.
    [Show full text]
  • The Dark Matter Crisis: Falsification of the Current Standard Model of Cosmology
    CSIRO PUBLISHING Publications of the Astronomical Society of Australia, 2012, 29, 395–433 Review http://dx.doi.org/10.1071/AS12005 The Dark Matter Crisis: Falsification of the Current Standard Model of Cosmology P. Kroupa Argelander Institute for Astronomy, University of Bonn, Auf dem Hu¨gel 71, 53121 Bonn, Germany Email: [email protected] Abstract: The current standard model of cosmology (SMoC) requires The Dual Dwarf Galaxy Theorem to be true according to which two types of dwarf galaxies must exist: primordial dark-matter (DM) dominated (type A) dwarf galaxies, and tidal-dwarf and ram-pressure-dwarf (type B) galaxies void of DM. Type A dwarfs surround the host approximately spherically, while type B dwarfs are typically correlated in phase- space. Type B dwarfs must exist in any cosmological theory in which galaxies interact. Only one type of dwarf galaxy is observed to exist on the baryonic Tully-Fisher plot and in the radius-mass plane. The Milky Way satellite system forms a vast phase-space-correlated structure that includes globular clusters and stellar and gaseous streams. Other galaxies also have phase-space correlated satellite systems. Therefore, The Dual Dwarf Galaxy Theorem is falsified by observation and dynamically relevant cold or warm DM cannot exist. It is shown that the SMoC is incompatible with a large set of other extragalactic observations. Other theoretical solutions to cosmological observations exist. In particular, alone the empirical mass-discrepancy— acceleration correlation constitutes convincing evidence
    [Show full text]
  • Observational Cosmology - 30H Course 218.163.109.230 Et Al
    Observational cosmology - 30h course 218.163.109.230 et al. (2004–2014) PDF generated using the open source mwlib toolkit. See http://code.pediapress.com/ for more information. PDF generated at: Thu, 31 Oct 2013 03:42:03 UTC Contents Articles Observational cosmology 1 Observations: expansion, nucleosynthesis, CMB 5 Redshift 5 Hubble's law 19 Metric expansion of space 29 Big Bang nucleosynthesis 41 Cosmic microwave background 47 Hot big bang model 58 Friedmann equations 58 Friedmann–Lemaître–Robertson–Walker metric 62 Distance measures (cosmology) 68 Observations: up to 10 Gpc/h 71 Observable universe 71 Structure formation 82 Galaxy formation and evolution 88 Quasar 93 Active galactic nucleus 99 Galaxy filament 106 Phenomenological model: LambdaCDM + MOND 111 Lambda-CDM model 111 Inflation (cosmology) 116 Modified Newtonian dynamics 129 Towards a physical model 137 Shape of the universe 137 Inhomogeneous cosmology 143 Back-reaction 144 References Article Sources and Contributors 145 Image Sources, Licenses and Contributors 148 Article Licenses License 150 Observational cosmology 1 Observational cosmology Observational cosmology is the study of the structure, the evolution and the origin of the universe through observation, using instruments such as telescopes and cosmic ray detectors. Early observations The science of physical cosmology as it is practiced today had its subject material defined in the years following the Shapley-Curtis debate when it was determined that the universe had a larger scale than the Milky Way galaxy. This was precipitated by observations that established the size and the dynamics of the cosmos that could be explained by Einstein's General Theory of Relativity.
    [Show full text]
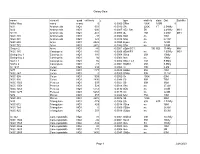
  • Galaxy Data Name Constell
    Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell.
    [Show full text]
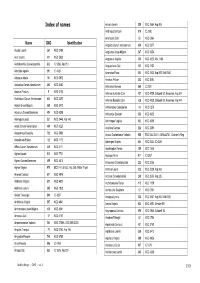
  • 190 Index of Names
    Index of names Ancora Leonis 389 NGC 3664, Arp 005 Andriscus Centauri 879 IC 3290 Anemodes Ceti 85 NGC 0864 Name CMG Identification Angelica Canum Venaticorum 659 NGC 5377 Accola Leonis 367 NGC 3489 Angulatus Ursae Majoris 247 NGC 2654 Acer Leonis 411 NGC 3832 Angulosus Virginis 450 NGC 4123, Mrk 1466 Acritobrachius Camelopardalis 833 IC 0356, Arp 213 Angusticlavia Ceti 102 NGC 1032 Actenista Apodis 891 IC 4633 Anomalus Piscis 804 NGC 7603, Arp 092, Mrk 0530 Actuosus Arietis 95 NGC 0972 Ansatus Antliae 303 NGC 3084 Aculeatus Canum Venaticorum 460 NGC 4183 Antarctica Mensae 865 IC 2051 Aculeus Piscium 9 NGC 0100 Antenna Australis Corvi 437 NGC 4039, Caldwell 61, Antennae, Arp 244 Acutifolium Canum Venaticorum 650 NGC 5297 Antenna Borealis Corvi 436 NGC 4038, Caldwell 60, Antennae, Arp 244 Adelus Ursae Majoris 668 NGC 5473 Anthemodes Cassiopeiae 34 NGC 0278 Adversus Comae Berenices 484 NGC 4298 Anticampe Centauri 550 NGC 4622 Aeluropus Lyncis 231 NGC 2445, Arp 143 Antirrhopus Virginis 532 NGC 4550 Aeola Canum Venaticorum 469 NGC 4220 Anulifera Carinae 226 NGC 2381 Aequanimus Draconis 705 NGC 5905 Anulus Grahamianus Volantis 955 ESO 034-IG011, AM0644-741, Graham's Ring Aequilibrata Eridani 122 NGC 1172 Aphenges Virginis 654 NGC 5334, IC 4338 Affinis Canum Venaticorum 449 NGC 4111 Apostrophus Fornac 159 NGC 1406 Agiton Aquarii 812 NGC 7721 Aquilops Gruis 911 IC 5267 Aglaea Comae Berenices 489 NGC 4314 Araneosus Camelopardalis 223 NGC 2336 Agrius Virginis 975 MCG -01-30-033, Arp 248, Wild's Triplet Aratrum Leonis 323 NGC 3239, Arp 263 Ahenea
    [Show full text]
  • Making a Sky Atlas
    Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it.
    [Show full text]
  • Ngc Catalogue Ngc Catalogue
    NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39
    [Show full text]
  • Explosion of the Science Modification of Newtonian Dynamics Via Mach's
    Physics International Original Research Paper Explosion of the Science Modification of Newtonian Dynamics Via Mach’s Inertia Principle and Generalization in Gravitational Quantum Bound Systems and Finite Range of the Gravity-Carriers, Consistent Merely On the Bosons and the Fermions Mohsen Lutephy Faculty of Science, Azad Islamic University (IAU), South Tehran branch, Iran Article history Abstract: Newtonian gravity is modified here via Mach's inertia principle Received: 29-04-2020 (inertia fully governed by universe) and it is generalized to gravitationally Revised: 11-05-2020 quantum bound systems, resulting scale invariant fully relational dynamics Accepted: 24-06-2020 (mere ordering upon actual objects), answering to rotation curves and velocity dispersions of the galaxies and clusters (large scale quantum bound Email: [email protected] systems), successful in all dimensions and scales from particle to the universe. Against the Milgrom’s theory, no fundamental acceleration to separate the physical systems to the low and large accelerations, on the contrary the Newtonian regime of HSB galaxies sourced by natural inertia constancy there. All phenomenological paradigms are argued here via Machian modified gravity generalized to quantum gravity, especially Milgrom empirical paradigms and even we have resolved the mystery of missing dark matter in newly discovered Ultra Diffuse Galaxies (UDGs) for potential hollow in host galaxy generated by sub quantum bound system of the globular clusters. Also we see that the strong nuclear force (Yukawa force) is in reality, the enhanced gravity for limitation of the gravitational potential because finite-range of the Compton wavelength of hadronic gravity-carriers in the nucleuses, reasoning to resolve ultimately, one of the biggest questions in the physics, that is, so called the fine structure constant and answering to mysterious saturation features of the nuclear forces and we have resolved also the mystery of the proton stability, reasonable as a quantum micro black hole and the exact calculation of the universe matter.
    [Show full text]
  • CURRICULUM VITAE Stacy S. Mcgaugh
    CURRICULUM VITAE Stacy S. McGaugh Department of Astronomy phone: (216) 368-1808 Case Western Reserve University fax: (216) 368-5406 Cleveland, OH 44106 cell: (216) 214-0686 http://astroweb.case.edu/ssm/ e-mail: [email protected] Education University of Michigan Ph.D. 1992 Astronomy 1987 { 1992 Princeton University Physics 1985 { 1986 Massachusetts Institute of Technology S.B. 1985 Physics 1981 { 1985 Employment Professor Departments of Astronomy & Physics 2012 { Chair Department of Astronomy 2015 { Director Warner & Swasey Observatory 2015 { Case Western Reserve University Professor Department of Astronomy 2009 { 2012 Associate Professor University of Maryland 2003 { 2009 Assistant Professor College Park 1998 { 2003 Research Fellow Department of Physics and Astronomy 1997 { 1998 Rutgers University Carnegie Fellow Department of Terrestrial Magnetism 1995 { 1997 Carnegie Institution of Washington Research Associate Institute of Astronomy 1992 { 1995 University of Cambridge Research Interests Galaxy formation and evolution, LSB galaxies, the missing mass problem, and cosmology Professional Societies | IAU, AAS, DDA Honors | Distinguished Alumnus, Flint Northern (2001); University of Michigan (2013) Publications in Refereed Journals The order of authors in Astronomy & Astrophysics reflects the degree of contribution. The names of directly supervised students and postdocs are italicized; McGaugh is listed in bold. Citation Statistics (as of 5 February 2020 from the NASA Astrophysical Data System): Total citations: 11,455; Normalized citations per author: 5,743 H-index: 57; riq index: 333; i100-index: 37 (papers with over 100 citations) 120. \A comprehensive catalog of dark matter halo models for SPARC galaxies" Li, P., Lelli, F., McGaugh, S.S., & Schombert, J.M. 2020, ApJS, in press 119.
    [Show full text]
  • Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S
    Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S. Mcgaugh To cite this version: Benoit Famaey, Stacy S. Mcgaugh. Modified Newtonian Dynamics (MOND): Observational Phe- nomenology and Relativistic Extensions. Living Reviews in Relativity, 2012, 15 (1), 10.12942/lrr- 2012-10. hal-02927744 HAL Id: hal-02927744 https://hal.archives-ouvertes.fr/hal-02927744 Submitted on 1 Sep 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Living Rev. Relativity, 15, (2012), 10 LIVINGREVIEWS http://www.livingreviews.org/lrr-2012-10 in relativity Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Beno^ıtFamaey Observatoire Astronomique de Strasbourg CNRS, UMR 7550, France and AIfA, University of Bonn, Germany email: [email protected] http://astro.u-strasbg.fr/~famaey/ Stacy S. McGaugh Department of Astronomy University of Maryland, USA and Case Western Reserve University, USA email: [email protected] http://astroweb.case.edu/ssm/ Accepted on 30 April 2012 Published on 7 September 2012 Abstract A wealth of astronomical data indicate the presence of mass discrepancies in the Universe. The motions observed in a variety of classes of extragalactic systems exceed what can be explained by the mass visible in stars and gas.
    [Show full text]
  • What Is Real?
    WHAT IS REAL? Space -Time Singularities or Quantum Black Holes? Dark Matter or Planck Mass Particles? General Relativity or Quantum Gravity? Volume or Area Entropy Law? BALUNGI FRANCIS Copyright © BalungiFrancis, 2020 The moral right of the author has been asserted. All rights reserved. Apart from any fair dealing for the purposes of research or private study or critism or review, no part of this publication may be reproduced, distributed, or transmitted in any form or by any means, including photocopying, recording, or other electronic or mechanical methods, or by any information storage and retrieval system without the prior written permission of the publisher. TABLE OF CONTENTS TABLE OF CONTENTS i DEDICATION 1 PREFACE ii Space-time Singularity or Quantum Black Holes? Error! Bookmark not defined. What is real? Is it Volume or Area Entropy Law of Black Holes? 1 Is it Dark Matter, MOND or Quantum Black Holes? 6 What is real? General Relativity or Quantum Gravity Error! Bookmark not defined. Particle Creation by Black Holes: Is it Hawking’s Approach or My Approach? Error! Bookmark not defined. Stellar Mass Black Holes or Primordial Holes Error! Bookmark not defined. Additional Readings Error! Bookmark not defined. Hidden in Plain sight1: A Simple Link between Quantum Mechanics and Relativity Error! Bookmark not defined. Hidden in Plain sight2: From White Dwarfs to Black Holes Error! Bookmark not defined. Appendix 1 Error! Bookmark not defined. Derivation of the Energy density stored in the Electric field and Gravitational Field Error!
    [Show full text]