The Distribution of Dark and Luminous Matter Inferred from Extended
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1. Introduction
THE ASTROPHYSICAL JOURNAL SUPPLEMENT SERIES, 122:109È150, 1999 May ( 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A. GALAXY STRUCTURAL PARAMETERS: STAR FORMATION RATE AND EVOLUTION WITH REDSHIFT M. TAKAMIYA1,2 Department of Astronomy and Astrophysics, University of Chicago, Chicago, IL 60637; and Gemini 8 m Telescopes Project, 670 North Aohoku Place, Hilo, HI 96720 Received 1998 August 4; accepted 1998 December 21 ABSTRACT The evolution of the structure of galaxies as a function of redshift is investigated using two param- eters: the metric radius of the galaxy(Rg) and the power at high spatial frequencies in the disk of the galaxy (s). A direct comparison is made between nearby (z D 0) and distant(0.2 [ z [ 1) galaxies by following a Ðxed range in rest frame wavelengths. The data of the nearby galaxies comprise 136 broad- band images at D4500A observed with the 0.9 m telescope at Kitt Peak National Observatory (23 galaxies) and selected from the catalog of digital images of Frei et al. (113 galaxies). The high-redshift sample comprises 94 galaxies selected from the Hubble Deep Field (HDF) observations with the Hubble Space Telescope using the Wide Field Planetary Camera 2 in four broad bands that range between D3000 and D9000A (Williams et al.). The radius is measured from the intensity proÐle of the galaxy using the formulation of Petrosian, and it is argued to be a metric radius that should not depend very strongly on the angular resolution and limiting surface brightness level of the imaging data. It is found that the metric radii of nearby and distant galaxies are comparable to each other. -

A Search For" Dwarf" Seyfert Nuclei. VII. a Catalog of Central Stellar
TO APPEAR IN The Astrophysical Journal Supplement Series. Preprint typeset using LATEX style emulateapj v. 26/01/00 A SEARCH FOR “DWARF” SEYFERT NUCLEI. VII. A CATALOG OF CENTRAL STELLAR VELOCITY DISPERSIONS OF NEARBY GALAXIES LUIS C. HO The Observatories of the Carnegie Institution of Washington, 813 Santa Barbara St., Pasadena, CA 91101 JENNY E. GREENE1 Department of Astrophysical Sciences, Princeton University, Princeton, NJ ALEXEI V. FILIPPENKO Department of Astronomy, University of California, Berkeley, CA 94720-3411 AND WALLACE L. W. SARGENT Palomar Observatory, California Institute of Technology, MS 105-24, Pasadena, CA 91125 To appear in The Astrophysical Journal Supplement Series. ABSTRACT We present new central stellar velocity dispersion measurements for 428 galaxies in the Palomar spectroscopic survey of bright, northern galaxies. Of these, 142 have no previously published measurements, most being rela- −1 tively late-type systems with low velocity dispersions (∼<100kms ). We provide updates to a number of literature dispersions with large uncertainties. Our measurements are based on a direct pixel-fitting technique that can ac- commodate composite stellar populations by calculating an optimal linear combination of input stellar templates. The original Palomar survey data were taken under conditions that are not ideally suited for deriving stellar veloc- ity dispersions for galaxies with a wide range of Hubble types. We describe an effective strategy to circumvent this complication and demonstrate that we can still obtain reliable velocity dispersions for this sample of well-studied nearby galaxies. Subject headings: galaxies: active — galaxies: kinematics and dynamics — galaxies: nuclei — galaxies: Seyfert — galaxies: starburst — surveys 1. INTRODUCTION tors, apertures, observing strategies, and analysis techniques. -
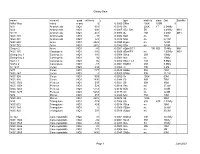
Galaxy Data Name Constell
Galaxy Data name constell. quadvel km/s z type width ly starsDist. Satellite Milky Way many many 0 0.0000 SBbc 106K 200M 0 M31 Andromeda NQ1 -301 -0.0010 SA 220K 1T 2.54Mly M32 Andromeda NQ1 -200 -0.0007 cE2 Sat. 5K 2.49Mly M31 M110 Andromeda NQ1 -241 -0.0008 dE 15K 2.69M M31 NGC 404 Andromeda NQ1 -48 -0.0002 SA0 no 10M NGC 891 Andromeda NQ1 528 0.0018 SAb no 27.3M NGC 680 Aries NQ1 2928 0.0098 E pec no 123M NGC 772 Aries NQ1 2472 0.0082 SAb no 130M Segue 2 Aries NQ1 -40 -0.0001 dSph/GC?. 100 5E5 114Kly MW NGC 185 Cassiopeia NQ1 -185 -0.0006dSph/E3 no 2.05Mly M31 Dwingeloo 1 Cassiopeia NQ1 110 0.0004 SBcd 25K 10Mly Dwingeloo 2 Cassiopeia NQ1 94 0.0003Iam no 10Mly Maffei 1 Cassiopeia NQ1 66 0.0002 S0pec E3 75K 9.8Mly Maffei 2 Cassiopeia NQ1 -17 -0.0001 SABbc 25K 9.8Mly IC 1613 Cetus NQ1 -234 -0.0008Irr 10K 2.4M M77 Cetus NQ1 1177 0.0039 SABd 95K 40M NGC 247 Cetus NQ1 0 0.0000SABd 50K 11.1M NGC 908 Cetus NQ1 1509 0.0050Sc 105K 60M NGC 936 Cetus NQ1 1430 0.0048S0 90K 75M NGC 1023 Perseus NQ1 637 0.0021 S0 90K 36M NGC 1058 Perseus NQ1 529 0.0018 SAc no 27.4M NGC 1263 Perseus NQ1 5753 0.0192SB0 no 250M NGC 1275 Perseus NQ1 5264 0.0175cD no 222M M74 Pisces NQ1 857 0.0029 SAc 75K 30M NGC 488 Pisces NQ1 2272 0.0076Sb 145K 95M M33 Triangulum NQ1 -179 -0.0006 SA 60K 40B 2.73Mly NGC 672 Triangulum NQ1 429 0.0014 SBcd no 16M NGC 784 Triangulum NQ1 0 0.0000 SBdm no 26.6M NGC 925 Triangulum NQ1 553 0.0018 SBdm no 30.3M IC 342 Camelopardalis NQ2 31 0.0001 SABcd 50K 10.7Mly NGC 1560 Camelopardalis NQ2 -36 -0.0001Sacd 35K 10Mly NGC 1569 Camelopardalis NQ2 -104 -0.0003Ibm 5K 11Mly NGC 2366 Camelopardalis NQ2 80 0.0003Ibm 30K 10M NGC 2403 Camelopardalis NQ2 131 0.0004Ibm no 8M NGC 2655 Camelopardalis NQ2 1400 0.0047 SABa no 63M Page 1 2/28/2020 Galaxy Data name constell. -

Optically Identified Supernova Remnants in the Nearby Spiral Galaxies NGC 5204, NGC 5585, NGC 6946, M81, and M101
Dartmouth College Dartmouth Digital Commons Open Dartmouth: Peer-reviewed articles by Dartmouth faculty Faculty Work 9-1997 Optically Identified Supernova Remnants in the Nearby Spiral Galaxies NGC 5204, NGC 5585, NGC 6946, M81, and M101 David M. Matonick Dartmouth College Robert A. Fesen Dartmouth College Follow this and additional works at: https://digitalcommons.dartmouth.edu/facoa Part of the Stars, Interstellar Medium and the Galaxy Commons Dartmouth Digital Commons Citation Matonick, David M. and Fesen, Robert A., "Optically Identified Supernova Remnants in the Nearby Spiral Galaxies NGC 5204, NGC 5585, NGC 6946, M81, and M101" (1997). Open Dartmouth: Peer-reviewed articles by Dartmouth faculty. 2307. https://digitalcommons.dartmouth.edu/facoa/2307 This Article is brought to you for free and open access by the Faculty Work at Dartmouth Digital Commons. It has been accepted for inclusion in Open Dartmouth: Peer-reviewed articles by Dartmouth faculty by an authorized administrator of Dartmouth Digital Commons. For more information, please contact [email protected]. THE ASTROPHYSICAL JOURNAL SUPPLEMENT SERIES, 112:49È107, 1997 September ( 1997. The American Astronomical Society. All rights reserved. Printed in U.S.A. OPTICALLY IDENTIFIED SUPERNOVA REMNANTS IN THE NEARBY SPIRAL GALAXIES NGC 5204, NGC 5585, NGC 6946, M81, AND M101 DAVID M. MATONICK AND ROBERT A. FESEN Department of Physics and Astronomy, 6127 Wilder Laboratory, Dartmouth College, Hanover, NH 03755 Received 1997 January 24; accepted 1997 April 11 ABSTRACT We present the results of an optical search for supernova remnants (SNRs) in the spiral galaxies NGC 5204, NGC 5585, NGC 6946, M81, and M101. Using the criterion that emission nebulae with [S II]/ Ha º 0.45 are identiÐed as SNRs, we found three SNRs in NGC 5204, Ðve in NGC 5585, 27 in NGC 6946, 41 in M81, and 93 in M101. -

190 Index of Names
Index of names Ancora Leonis 389 NGC 3664, Arp 005 Andriscus Centauri 879 IC 3290 Anemodes Ceti 85 NGC 0864 Name CMG Identification Angelica Canum Venaticorum 659 NGC 5377 Accola Leonis 367 NGC 3489 Angulatus Ursae Majoris 247 NGC 2654 Acer Leonis 411 NGC 3832 Angulosus Virginis 450 NGC 4123, Mrk 1466 Acritobrachius Camelopardalis 833 IC 0356, Arp 213 Angusticlavia Ceti 102 NGC 1032 Actenista Apodis 891 IC 4633 Anomalus Piscis 804 NGC 7603, Arp 092, Mrk 0530 Actuosus Arietis 95 NGC 0972 Ansatus Antliae 303 NGC 3084 Aculeatus Canum Venaticorum 460 NGC 4183 Antarctica Mensae 865 IC 2051 Aculeus Piscium 9 NGC 0100 Antenna Australis Corvi 437 NGC 4039, Caldwell 61, Antennae, Arp 244 Acutifolium Canum Venaticorum 650 NGC 5297 Antenna Borealis Corvi 436 NGC 4038, Caldwell 60, Antennae, Arp 244 Adelus Ursae Majoris 668 NGC 5473 Anthemodes Cassiopeiae 34 NGC 0278 Adversus Comae Berenices 484 NGC 4298 Anticampe Centauri 550 NGC 4622 Aeluropus Lyncis 231 NGC 2445, Arp 143 Antirrhopus Virginis 532 NGC 4550 Aeola Canum Venaticorum 469 NGC 4220 Anulifera Carinae 226 NGC 2381 Aequanimus Draconis 705 NGC 5905 Anulus Grahamianus Volantis 955 ESO 034-IG011, AM0644-741, Graham's Ring Aequilibrata Eridani 122 NGC 1172 Aphenges Virginis 654 NGC 5334, IC 4338 Affinis Canum Venaticorum 449 NGC 4111 Apostrophus Fornac 159 NGC 1406 Agiton Aquarii 812 NGC 7721 Aquilops Gruis 911 IC 5267 Aglaea Comae Berenices 489 NGC 4314 Araneosus Camelopardalis 223 NGC 2336 Agrius Virginis 975 MCG -01-30-033, Arp 248, Wild's Triplet Aratrum Leonis 323 NGC 3239, Arp 263 Ahenea -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Atlante Grafico Delle Galassie
ASTRONOMIA Il mondo delle galassie, da Kant a skylive.it. LA RIVISTA DELL’UNIONE ASTROFILI ITALIANI Questo è un numero speciale. Viene qui presentato, in edizione ampliata, quan- [email protected] to fu pubblicato per opera degli Autori nove anni fa, ma in modo frammentario n. 1 gennaio - febbraio 2007 e comunque oggigiorno di assai difficile reperimento. Praticamente tutte le galassie fino alla 13ª magnitudine trovano posto in questo atlante di più di Proprietà ed editore Unione Astrofili Italiani 1400 oggetti. La lettura dell’Atlante delle Galassie deve essere fatto nella sua Direttore responsabile prospettiva storica. Nella lunga introduzione del Prof. Vincenzo Croce il testo Franco Foresta Martin Comitato di redazione e le fotografie rimandano a 200 anni di studio e di osservazione del mondo Consiglio Direttivo UAI delle galassie. In queste pagine si ripercorre il lungo e paziente cammino ini- Coordinatore Editoriale ziato con i modelli di Herschel fino ad arrivare a quelli di Shapley della Via Giorgio Bianciardi Lattea, con l’apertura al mondo multiforme delle altre galassie, iconografate Impaginazione e stampa dai disegni di Lassell fino ad arrivare alle fotografie ottenute dai colossi della Impaginazione Grafica SMAA srl - Stampa Tipolitografia Editoria DBS s.n.c., 32030 metà del ‘900, Mount Wilson e Palomar. Vecchie fotografie in bianco e nero Rasai di Seren del Grappa (BL) che permettono al lettore di ripercorrere l’alba della conoscenza di questo Servizio arretrati primo abbozzo di un Universo sempre più sconfinato e composito. Al mondo Una copia Euro 5.00 professionale si associò quanto prima il mondo amatoriale. Chi non è troppo Almanacco Euro 8.00 giovane ricorderà le immagini ottenute dal cielo sopra Bologna da Sassi, Vac- Versare l’importo come spiegato qui sotto specificando la causale. -

Dust Temperatures in the Infrared Space Observatory1atlas of Bright Spiral Galaxies
Dust Temperatures in the Infrared Space Observatory1Atlas of Bright Spiral Galaxies George J. Bendo,2;3;4 Robert D. Joseph,3 Martyn Wells,5 Pascal Gallais,6 Martin Haas,7 Ana M. Heras,8;9 Ulrich Klaas,7 Ren´eJ.Laureijs,8;9 Kieron Leech,9;10 Dietrich Lemke,7 Leo Metcalfe,8 Michael Rowan-Robinson,11 Bernhard Schulz,9;12 and Charles Telesco13 ABSTRACT We examine far-infrared and submillimeter spectral energy distributions for galaxies in the Infrared Space Observatory Atlas of Bright Spiral Galaxies. For the 71 galaxies where we had complete 60 - 180 µm data, 1 2 we fit blackbodies with λ− emissivities and average temperatures of 31 K or λ− emissivities and average temperatures of 22 K. Except for high temperatures determined in some early-type galaxies, the temperatures show no dependence on any galaxy characteristic. For the 60 - 850 µm range in eight galaxies, we fit blackbodies 1 2 β β with λ− , λ− ,andλ− (with β variable) emissivities to the data. The best results were with the λ− emissivities, where the temperatures were 30 K and the emissivity coefficient β ranged from 0.9 to 1.9. These results produced gas to dust ratios that∼ ranged from 150 to 580, which were consistent with the ratio for the Milky Way and which exhibited relatively little dispersion compared to fits with fixed emissivities. Subject headings: galaxies: ISM | galaxies: spiral | dust 1. Introduction 2Steward Observatory, 933 North Cherry Ave, Tucson, AZ 85721 USA; [email protected] The far-infrared emission from galaxies is emitted by 3University of Hawaii, Institute for Astronomy, 2680 Woodlawn interstellar dust heated by a variety of energy sources. -

Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S
Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Benoit Famaey, Stacy S. Mcgaugh To cite this version: Benoit Famaey, Stacy S. Mcgaugh. Modified Newtonian Dynamics (MOND): Observational Phe- nomenology and Relativistic Extensions. Living Reviews in Relativity, 2012, 15 (1), 10.12942/lrr- 2012-10. hal-02927744 HAL Id: hal-02927744 https://hal.archives-ouvertes.fr/hal-02927744 Submitted on 1 Sep 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Living Rev. Relativity, 15, (2012), 10 LIVINGREVIEWS http://www.livingreviews.org/lrr-2012-10 in relativity Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions Beno^ıtFamaey Observatoire Astronomique de Strasbourg CNRS, UMR 7550, France and AIfA, University of Bonn, Germany email: [email protected] http://astro.u-strasbg.fr/~famaey/ Stacy S. McGaugh Department of Astronomy University of Maryland, USA and Case Western Reserve University, USA email: [email protected] http://astroweb.case.edu/ssm/ Accepted on 30 April 2012 Published on 7 September 2012 Abstract A wealth of astronomical data indicate the presence of mass discrepancies in the Universe. The motions observed in a variety of classes of extragalactic systems exceed what can be explained by the mass visible in stars and gas. -

Studies of the Stellar Populations of Galaxies Using Two-Color Diagrams
Astronomy Reports, 2015, Vol. 59, No. 10, pp. 899-919 June 24, 2021 Translated from Astronomicheskii Zhurnal, 2015, Vol. 92, No. 10, pp. 779-799 Studies of the Stellar Populations of Galaxies Using Two-Color Diagrams A. S. Gusev,1 S. A. Guslyakova,2 A. P. Novikova,1 M. S. Khramtsova,3 V. V. Bruevich,1 O. V. Ezhkova1 1 Sternberg Astronomical Institute, Lomonosov Moscow University, Universitetskii pr. 13, Moscow 119992 Russia 2 Space Research Institute, Russian Academy of Sciences, 84/32 Profsoyuznaya Str, Moscow 117997, Russia 3 Institute of Astronomy, Russian Academy of Sciences, Pyatnitskaya 48, Moscow 119017, Russia Received December 12, 2014; in final form, March 13, 2015 Abstract. Variations in the photometric parameters of stellar systems as a function of their evolution and the stellar populations comprising them are investigated. A set of seven evolutionary models with an exponential decrease in the star-formation rate and 672 models with a secondary burst of star formation are considered. The occurrence of a secondary burst of star formation can shift the position of a stellar system on two-color diagrams to the right or left of the normal color sequence for galaxies and the extinction line. This makes it possible to estimate the composition of the stellar population of a galaxy with a nonmonotonic star-formation history from its position on two-color diagrams. Surface photometry in both the optical (UBV RI) and near-IR (JHK) is used to study the stellar populations and star-formation histories in the structural components (nucleus, bulge, disk, spiral arms, bar, ring) of 26 galaxies of various morphological types (from S0 to Sd). -

TABLE 1 Explanation of CVRHS Symbols A
TABLE 1 Explanation of CVRHS Symbols a Symbol Description 1 2 General Terms ETG An early-type galaxy, collectively referring to a galaxy in the range of types E to Sa ITG An intermediate-type galaxy, taken to be in the range Sab to Sbc LTG A late-type galaxy, collectively referring to a galaxy in the range of types Sc to Im ETS An early-type spiral, taken to be in the range S0/a to Sa ITS An intermediate-type spiral, taken to be in the range Sab to Sbc LTS A late-type spiral, taken to be in the range Sc to Scd XLTS An extreme late-type spiral, taken to be in the range Sd to Sm classical bulge A galaxy bulge that likely formed from early mergers of smaller galaxies (Kormendy & Kennicutt 2004; Athanassoula 2005) pseudobulge A galaxy bulge made of disk material that has secularly collected into the central regions of a barred galaxy (Kormendy 2012) PDG A pure disk galaxy, a galaxy lacking a classical bulge and often also lacking a pseudobulge Stage stage The characteristic of galaxy morphology that recognizes development of structure, the widespread distribution of star formation, and the relative importance of a bulge component along a sequence that correlates well with basic characteristics such as integrated color, average surface brightness, and HI mass-to-blue luminosity ratio Elliptical Galaxies E galaxy A galaxy having a smoothly declining brightness distribution with little or no evidence of a disk component and no inflections (such as lenses) in the luminosity distribution (examples: NGC 1052, 3193, 4472) En An elliptical galaxy