DOCSLIB.ORG

Introduction to Waveguide Optics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction to Waveguide Optics 2572-4 Winter College on Optics: Fundamentals of Photonics - Theory, Devices and Applications 10 - 21 February 2014 Introduction to Waveguide Optics Jiri Ctroky Institute of Photonics and Electronics AS CR, v.v.i., Prague Czech Republic IntroductiontoWaveguideOptics JiƎítyroký [email protected] Instituteof Photonics and Electronics AS CR, v.v.i., Prague,CzechRepublic WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy WhereIcomefrom… InstituteofPhotonics andElectronicsASCR,v.v.i. AcademyofSciencesoftheCzechRepublicisanonͲuniversityinstitutionforbasicandappliedresearchconsistingof54independentinstitutes WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 1 Examplesofwaveguidestructures opticalfibre channeloptical “ARROW” waveguide (antiresonantreflectingOW) longitudinally uniform microring angularly plasmonicwaveguide resonator uniform metal subwavelengthgrating photoniccrystal waveguide waveguide “gain/loss”waveguide loss gain longitudinally periodic etc… WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Theoreticalfundamentalsofopticalwaveguides Tentativelistoftopics • Planarwaveguides;waveguidemodes,theirproperties.Guidedandleakymodes. Othertypesofwaveguiding,guidingbyasingleinterface • Waveguidebends,whisperingͲgallerymodes,circularresonators • Channelwaveguides,approximateanalyticalmethods. • Morecomplexwaveguidestructures.FundamentalsofarigorouscoupledͲmodetheory • Introductiontomodalmethods;transfermatrixmethod,basicsofthefilmmodematching • Periodicmedia,Blochmodes,originofthebandgap,SWGwaveguides,(photoniccrystals) • “Canonical”waveguidestructures:YͲjunctions,directionalcoupler,twoͲ andmultimode interferencecouplers,microresonators • Plasmonicwaveguidesandstructures.Surfaceplasmonsensing.HybriddielectricͲplasmonic slotwaveguide,plasmonicdevices • Waveguidestructureswithlossandgain;asymmetricgratingcouplers,(“PTͲsymmetric” waveguidestructures) • … Basicrequirements:Theoryofelectromagneticfield,Maxwellequations WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 2 Basicmath&physbackground Dielectric(possiblyalsometallic)nonͲmagneticlinearsourceͲfreemedium, timeͲharmonicdependenceofelectromagneticfield: (,)rErtit Re ()exp(Z ) E ^ ` uEH iZP0 ,0 D (,)rHrtit Re^` ()exp(Z ) 2 H uHEB inZH0 ,0 22 2S k ZPH DE H n2 000O 0 22 BH P0 kk 00H kn 1 kn (phase velocity) PlaneͲwavesolution: vcZ iikr kccc r k r EE 00eee E 1 dk ng (group velocity) iikr kccc r k r vdg Z c HH 00eee E dn()Z dn 2 nn Z group index kk cccini k, H cccH g ddZZ cccc222 dn kk k0 H complex nnO , typically larger than 2 wavevector dO 2kkccc k0 H cc WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Fieldattheinterfacebetweentwomedia Planewaveincidentonaplanarinterface iiiikrititiikrr kr kr krr kr EEii 000e, EE rr e, EE tt e, HH i i 0 e, H r H r 0 e, HH t t 0 e TEpolarization x k x E k E t TMpolarization t t EHH,, t n n yxz 2 H yxz,,EE 2 Ht H z z t nn E n 12 E r 1 k r n ki R E i R H 1 i H k i i r k Ei r r r Hi Hi 00 00222222 kxzkxzir,01 kN rJJJJ ir ,, t kNNnNn 02 t, 1 ir ,1 , t t 2 Fieldcontinuityconditionsat x 0: 0000 0 0 izkziiizkzrr iz kz iz kz iz kz r iz kz r Eeir000 Ee Ee t, He i 0 H r 0 e He t 0 NNNNn sinT 22 22 irt1 i JJ11 nN, 2 nN 2 WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 3 Fresnelcoefficients 22 TE Er J12 J TM Hnnr JJ11 2 2 R R 22 Ei JJ12 Hi JJ11nn 2 2 22 22 nN12 nN 22 2 22 2 nn21 N nn 1 2 N 22 22 nN12 nN 22 2 22 2 nn21 N nn 1 2 N criticalangle ) | TM TM totalreflection R ( R | , | , arg TE ) R | TE R arg( “regionofinterest” ofwaveguideoptics Brewster angle Angle of incidence (deg) Angle of incidence (deg) TM TM i ) TE Re ; TE i ) Re ; 2 ªº22 22 TM §·nNn12 N n ) 2arctan«»¨¸ . )TE 2arctan2 . «»n nN22 22 ¬¼©¹2 1 nN1 WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Thesimplestwaveguide:two(perfect)conductors x R kxzr kN(),rJ 00 d 0 k E k RTE yref, 1 0 z E y R yinc, perfectconductors Twoequivalentphysicalpictures: TM H yref, R 1 1.aseriesofsuccessivereflectionsofaplanewave H yinc, 2.twoplanewavespropagatingupwardsanddownwards Inbothcases,the“nonzerowave”inthewaveguidecanexistonlyunder the“conditionoftransverseresonance” (forTMonly) 2 Rikdexp(200JJS ) 1, or 2 kdmm 2 , 0, 1, 2, ! Wavescanthuspropagateonlyasdiscretewaveguidemodes withpropagationconstants EETE TM kN22 k 2 k 22 J k 2 m S d2 …polarizationdegeneracy mm00 m m (exceptform =0) for md! 2O …evanescentmodes ExzEym(,) 0 sin mxdSE exp( i z ) Thetransversefielddistributionshavetheforms H ym(,)xz H0 cos mSE xd exp( i z ) WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 4 Dielectric slab waveguide x nnncswdd Total reflection at both interfaces: nNnwcs!!, 22 22 nc JJw nN w, cs,, iNn cs R c d Condition of transverse resonance: nw z 0 R RRexp(2 ikJ d ) 1, or ns s cs0 w 11 )()Nkd J arg R arg R S m tot0 w22 s c ªºªºQQ22 22 22 §·nNnwms §· nNn wmC ­ 0 (TE) kd0 nwm N arctan«»«»¨¸ arctan ¨¸ mS , Q ® «»«»nnnN22 nN 22 2 (TM) ¬¼¬¼©¹scwm ©¹ wm ¯ TE TM Dispersion equation for Nm shows polarization birefringence, NNmm! WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Effectivethickness&“periodofpropagation” x Total internal reflection is linked up ddR) 1(arg) LGHa LGH with the Goos-Hänchen shift, dkdNE 0 k0 J a ªºNn22 TE 22dN«»sc, d LGHs,c arctan , kdN«»22 22 2 2 z d 0 nNw kNn() nN 0 eff ¬¼0,csw L k J ªº2 Nn22 GHs 0 s TM 2 d «»nw sc, LGHs,c arctan 222 kdN0 «»nnN Lp ¬¼sc, w 2N nn22() n 2 n 2 wsc,, w sc . 22 2 2nn42 N 2 nNn 422 kNn0, sc nN w s,,cw w sc TE ddkeff 0 J s J c (and a similar, somewhat more complicated expression for TM) – effective thickness d)tot 2 dk 0J w d N Lp LLGSs GSc 2 d LL GSs GSc … “period of propagation” dkdNE 22 0 nNw These “ray-optic concepts” are useful also for inherently “wave-optic” phenomenon of optical waveguiding. WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 5 Dispersion diagram (examples) Asymmetricwaveguide 1,60 TE0 nn 11.51.6 n TM cs w 1,58 0 All modes exhibit cut-off 1 1,56 2 3 eff 4 N 1,54 5 6 1.60 7 1,52 TE 8 0 TM 9 1.58 0 10 1 1,50 2 0246810 eff 1.56 3 N 4 d/O 1.54 5 6 7 Symmetric waveguide 1.52 8 9 nncs15.. n w 16 10 1.50 Number of TE and TM modes identical, 0246810 TE and TM always exist d/O 0 0 WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Distributionofmodesofaslabwaveguide TE guiding layer 0.2 0 TE 1 TE 2 0.1 TE 3 TE 4 0.0 substrate cover Mode field amplitude -0.1 n = 1,5 n = 1,0 s c -0.2 n = 1,6 w -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 x coordinate (μm) WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 6 Electromagnetic theory of a slab waveguide w Planarwaveguideasastructurewith1Dpermittivtydistribution:H ();x { 0 wy 1.TEpolarization: EHHyxz,, 2.TMpolarization: H yxz,,EE izE Eigenmodefield: ExzExyy(,) ()e , etc. i dE() x i dHy () x Hx() y , Ex() , z z 2 dx ZP0 dx ZH0nx() E E Hxxy() Ex (), Exxy() 2 Hx (), ZP0 ZH0nx() dH() x dE() x z iHEZH() x i n2 () xEx () z iEEZP() x i H () x dx xy0 dx xy0 ­½d 2 ­½ddªº1 kn22 x E x E 2 E x °°2222 ®¾2 0 yy ®¾nx «»2 knxHx0 ()yy E Hx () ¯¿dx ¯¿°°dx¬¼«»nx dx 2 EigenvalueequationsforeigenfunctionsExyy() or Hx()andeigenvaluesE WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Analogybetweenaplanarwaveguide andapotentialwellinquantummechanics FieldequationforaTEmode Schrödingerequationforaparticle inaplanarwaveguide inapotentialwell 2 22 1()dEy 22 = dx\ 22nxE()yy NE 2 Vx()\\ () x W () x kdx0 2m dx Ex() \ ()x y Thereisnotsuchanexactanalogy 2m forTMpolarization,butitsbehaviour k isverysimilar nx2 () 0 = 2 2 nx() Vx() Vx() N0 guidedmodes 2 N 2 W x N1 substratemode freeparticle reflectionfrom radiationmode thepotentialbarrier W x 1 boundstates W0 WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy 7 Guidingofopticalradiationinadielectric waveguide x guided substrate superstrate mode mode mode nc nc nx() 0 nw nw guidedmode ns ns “substrate”mode Guidedmodes: kn00csd knE kn 0 g radiationmode Radiation (substrate) modes: kn000csgE kn kn Radiationmodes(superstrate): E dkn000csg kn kn WINTER COLLEGE on OPTICS: Fundamentals of Photonics - Theory,Devices and Applications, 10 - 21 February 2014, Trieste - Miramare, Italy Orthogonality of eigenmodes Itcanbeshownthatfieldsofguidedmodes (fromthediscretespectrum) areorthogonal, 1 f E EHz()x u ()xdx0 m GE , kN. 2 ³ mnE mnmm0 f m Forradiationandevanescentmodes,theorthogonalityconditionsounds f 1 E (inthesense EH(,xxdxEE )u (,cc ) z0 G (EE ) 2 ³ n E oftheprincipalvalue f oftheintegral) Radiationandevanescentmodes arealwaysorthogonal todiscreteguidedmodes: 1 f EHz(,xxdxE )u ()0 0, 2 ³ n f Forlosslesswaveguides,
Load more

Recommended publications
  • Lecture 17 - Rectangular Waveguides/Photonic Crystals� and Radiative Recombination -Outline�
    6.772/SMA5111 - Compound Semiconductors Lecture 17 - Rectangular Waveguides/Photonic Crystals� and Radiative Recombination -Outline� • Dielectric optics (continuing discussion in Lecture 16) Rectangular waveguides� Coupled rectangular waveguide structures Couplers, Filters, Switches • Photonic crystals History: Optical bandgaps and Eli Yablonovich, to the present One-dimensional photonic crystals� Distributed Bragg reflectors� Photonic fibers; perfect mirrors� Two-dimensional photonic crystals� Guided wave optics structures� Defect levels� Three-dimensional photonic crystals • Recombination Processes (preparation for LEDs and LDs) Radiative vs. non-radiative� Relative carrier lifetimes� C. G. Fonstad, 4/03 Lecture 17 - Slide 1 Absorption in semiconductors - indirect-gap band-to-band� •� The phonon modes involved indirect band gap absorption •� Dispersion curves for acoustic and optical phonons Approximate optical phonon energies for several semiconductors Ge: 37 meV (Swaminathan and Macrander) Si: 63 meV GaAs: 36 meV C. G. Fonstad, 4/03� Lecture 15 - Slide 2� Slab dielectric waveguides� •�Nature of TE-modes (E-field has only a y-component). For the j-th mode of the slab, the electric field is given by: - (b -w ) = j j z t E y, j X j (x)Re[ e ] In this equation: w: frequency/energy of the light pw = n = l 2 c o l o: free space wavelength� b j: propagation constant of the j-th mode Xj(x): mode profile normal to the slab. satisfies d 2 X j + 2 2- b 2 = 2 (ni ko j )X j 0 dx where:� ni: refractive index in region i� ko: propagation constant in free space = pl ko 2 o C. G. Fonstad, 4/03� Lecture 17 - Slide 3� Slab dielectric waveguides� •�In approaching a slab waveguide problem, we typically take the dimensions and indices in the various regions and the free space wavelength or frequency of the light as the "givens" and the unknown is b, the propagation constant in the slab.
    [Show full text]
  • Lecture 26 Dielectric Slab Waveguides
    Lecture 26 Dielectric Slab Waveguides In this lecture you will learn: • Dielectric slab waveguides •TE and TM guided modes in dielectric slab waveguides ECE 303 – Fall 2005 – Farhan Rana – Cornell University TE Guided Modes in Parallel-Plate Metal Waveguides r E()rr = yˆ E sin()k x e− j kz z x>0 o x x Ei Ei r r Ey k E r k i r kr i H Hi i z ε µo Hr r r ki = −kx xˆ + kzzˆ kr = kx xˆ + kzzˆ Guided TE modes are TE-waves bouncing back and fourth between two metal plates and propagating in the z-direction ! The x-component of the wavevector can have only discrete values – its quantized m π k = where : m = 1, 2, 3, x d KK ECE 303 – Fall 2005 – Farhan Rana – Cornell University 1 Dielectric Waveguides - I Consider TE-wave undergoing total internal reflection: E i x ε1 µo r k E r i r kr H θ θ i i i z r H r ki = −kx xˆ + kzzˆ r kr = kx xˆ + kzzˆ Evanescent wave ε2 µo ε1 > ε2 r E()rr = yˆ E e− j ()−kx x +kz z + yˆ ΓE e− j (k x x +kz z) 2 2 2 x>0 i i kz + kx = ω µo ε1 Γ = 1 when θi > θc When θ i > θ c : kx = − jα x r E()rr = yˆ T E e− j kz z e−α x x 2 2 2 x<0 i kz − α x = ω µo ε2 ECE 303 – Fall 2005 – Farhan Rana – Cornell University Dielectric Waveguides - II x ε2 µo Evanescent wave cladding Ei E ε1 µo r i r k E r k i r kr i core Hi θi θi Hi ε1 > ε2 z Hr cladding Evanescent wave ε2 µo One can have a guided wave that is bouncing between two dielectric interfaces due to total internal reflection and moving in the z-direction ECE 303 – Fall 2005 – Farhan Rana – Cornell University 2 Dielectric Slab Waveguides W 2d Assumption: W >> d x cladding y core
    [Show full text]
  • High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium
    Progress In Electromagnetics Research C, Vol. 79, 115–126, 2017 High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium Adel A. A. Abdelrehim and Hooshang Ghafouri-Shiraz* Abstract—In this paper, a new high performance slotted waveguide antenna incorporated with negative refractive index metamaterial structure is proposed, designed and experimentally demonstrated. The metamaterial structure is constructed from a multilayer two-directional structure of electrically split ring resonator which exhibits negative refractive index in direction of the radiated wave propagation when it is placed in front of the slotted waveguide antenna. As a result, the radiation beams of the slotted waveguide antenna are focused in both E and H planes, and hence the directivity and the gain are improved, while the beam area is reduced. The proposed antenna and the metamaterial structure operating at 10 GHz are designed, optimized and numerically simulated by using CST software. The effective parameters of the eSRR structure are extracted by Nicolson Ross Weir (NRW) algorithm from the s-parameters. For experimental verification, a proposed antenna operating at 10 GHz is fabricated using both wet etching microwave integrated circuit technique (for the metamaterial structure) and milling technique (for the slotted waveguide antenna). The measurements are carried out in an anechoic chamber. The measured results show that the E plane gain of the proposed slotted waveguide antenna is improved from 6.5 dB to 11 dB as compared to the conventional slotted waveguide antenna. Also, the E plane beamwidth is reduced from 94.1 degrees to about 50 degrees.
    [Show full text]
  • Waveguide Direction User Manual
    WaveGuide Direction Ex. Certified User Manual WaveGuide Direction Ex. Certified User Manual Applicable for product no. WG-DR40-EX Related to software versions: wdr 4.#-# Version 4.0 21st of November 2016 Radac B.V. Elektronicaweg 16b 2628 XG Delft The Netherlands tel: +31(0)15 890 3203 e-mail: [email protected] website: www.radac.nl Preface This user manual and technical documentation is intended for engineers and technicians involved in the software and hardware setup of the Ex. certified version of the WaveGuide Direction. Note All connections to the instrument must be made with shielded cables with exception of the mains. The shielding must be grounded in the cable gland or in the terminal compartment on both ends of the cable. For more information regarding wiring and cable specifications, please refer to Chapter 2. Legal aspects The mechanical and electrical installation shall only be carried out by trained personnel with knowledge of the local requirements and regulations for installation of electronic equipment. The information in this installation guide is the copyright property of Radac BV. Radac BV disclaims any responsibility for personal injury or damage to equipment caused by: Deviation from any of the prescribed procedures. • Execution of activities that are not prescribed. • Neglect of the general safety precautions for handling tools and use of electricity. • The contents, descriptions and specifications in this installation guide are subject to change without notice. Radac BV accepts no responsibility for any errors that may appear in this user manual. Additional information Please do not hesitate to contact Radac or its representative if you require additional information.
    [Show full text]
  • High-Index Glass Waveguides for AR Roadmap to Consumer Market
    High-Index Glass Waveguides for AR Roadmap to Consumer Market Dr. Xavier Lafosse Commercial Technology Director, Advanced Optics SPIE AR / VR / MR Conference February 2-4, 2020 Outline • Enabling the Display Industry Through Glass Innovations • Our Solutions for Augmented Reality Applications • The Challenges for Scalable and Cost-Effective Solutions Precision Glass Solutions © 2020 Corning Incorporated 2 Corning’s glass innovations have enabled displays for more than 80 years… 1939 1982 2019 Cathode ray tubes for Liquid crystal display (LCD) EAGLE XG® Glass is the black and white televisions glass for monitors, laptops LCD industry standard Precision Glass Solutions © 2020 Corning Incorporated 3 Corning is a world-renowned innovator and supplier across the display industry Cover Glass Glass For AR/MR Display for Display Waveguides Display Technologies Introduced glass panels for 1st active 12 years of innovation in cover Corning Precision Glass Solutions matrix LCD devices in 1980s glass for smartphones, laptops, (PGS) was the first to market with tablets & wearables ultra-flat, high-index wafers for top- Have sold 25 billion square feet of tier consumer electronic companies ® ® ® ® flagship Corning EAGLE XG Corning Gorilla Glass is now on pursuing augmented reality and more than 7 billion devices worldwide mixed reality waveguide displays Precision Glass Solutions © 2020 Corning Incorporated 4 PGS offers best-in-class glass substrates for semiconductor and consumer electronics applications Advanced Low-loss, low Wafer-level Waveguide
    [Show full text]
  • Instruction Manual Waveguide & Waveguide Server
    Instruction manual WaveGuide & WaveGuide Server Radac bv Elektronicaweg 16b 2628 XG DELFT Phone: +31 15 890 32 03 Email: [email protected] www.radac.n l Instruction manual WaveGuide + WaveGuide Server Version 4.1 2 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Version 4.1 3 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Table of Contents Introduction...................................................................................................................................................................4 Installation.....................................................................................................................................................................5 The WaveGuide Sensor...........................................................................................................................................5 CaBling.....................................................................................................................................................................6 The WaveGuide Server............................................................................................................................................7 Commissioning the system...........................................................................................................................................9 Connect the WGS to a computer.............................................................................................................................9 Authorization.........................................................................................................................................................10
    [Show full text]
  • Analysis of a Waveguide-Fed Metasurface Antenna
    Analysis of a Waveguide-Fed Metasurface Antenna Smith, D., Yurduseven, O., Mancera, L. P., Bowen, P., & Kundtz, N. B. (2017). Analysis of a Waveguide-Fed Metasurface Antenna. Physical Review Applied, 8(5). https://doi.org/10.1103/PhysRevApplied.8.054048 Published in: Physical Review Applied Document Version: Publisher's PDF, also known as Version of record Queen's University Belfast - Research Portal: Link to publication record in Queen's University Belfast Research Portal Publisher rights © 2017 American Physical Society. This work is made available online in accordance with the publisher’s policies. Please refer to any applicable terms of use of the publisher. General rights Copyright for the publications made accessible via the Queen's University Belfast Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy The Research Portal is Queen's institutional repository that provides access to Queen's research output. Every effort has been made to ensure that content in the Research Portal does not infringe any person's rights, or applicable UK laws. If you discover content in the Research Portal that you believe breaches copyright or violates any law, please contact [email protected]. Download date:02. Oct. 2021 PHYSICAL REVIEW APPLIED 8, 054048 (2017) Analysis of a Waveguide-Fed Metasurface Antenna † † David R. Smith,* Okan Yurduseven, Laura Pulido Mancera, and Patrick Bowen Department of Electrical and Computer Engineering, Duke University, Durham, North Carolina 27708, USA Nathan B.
    [Show full text]
  • University of California Santa Cruz Distributed Bragg
    UNIVERSITY OF CALIFORNIA SANTA CRUZ DISTRIBUTED BRAGG REFLECTOR ON ARROW WAVEGUIDES A thesis submitted in partial satisfaction of the requirements for the degree of BACHELOR OF SCIENCE in PHYSICS by Raul A. Reyes Hueros June 2018 The thesis of Raul A. Reyes Hueros is approved: Professor Robert P. Johnson, Chair Professor Holger Schmidt Professor David Smith Copyright c by Raul A. Reyes Hueros 2018 Abstract Distributed Bragg Reflector on ARROW Waveguides by Raul A. Reyes Hueros A new optofluidic chip design for an on-chip liquid dye laser based on Anti- Resonant Reflecting Optical Waveguides (ARROW) is developed. The microfluidic device is compact, user friendly and, most importantly, can provide the role of a on chip laser. This thesis can be broken into three parts: First, an analysis on distributive feed back (DFB) gratings that is developed to fabricate a optofluidic dye laser from anti-resonant reflecting optical waveguides (ARROW). Second, the reflection spectrum and plausible parameters for the proposed device are simulated with Roaurd's Method. Third, a technique for direct dry transfer of uniform poly (methyl methacrylate) (PMMA) is used to overcome the challenges encountered in conventional PMMA deposition on top of non-flat waveguide structures. Table of Contents Abstract iii List of Figures vi List of Tables viii Acknowledgments ix 1 Introduction 1 1.1 Motivations for Building On-chip Bragg Reflector . 2 1.2 Thesis Organization . 3 2 Background 4 2.1 Distributed Bragg Reflector Gratings . 4 2.2 Organic Dye Molecules . 7 2.2.1 Population Inversion . 7 2.3 Liquid Dye Laser . 9 3 Anti-Resonant Reflecting Optical Waveguides 12 3.1 Theory .
    [Show full text]
  • Waveguide Propagation
    NTNU Institutt for elektronikk og telekommunikasjon Januar 2006 Waveguide propagation Helge Engan Contents 1 Introduction ........................................................................................................................ 2 2 Propagation in waveguides, general relations .................................................................... 2 2.1 TEM waves ................................................................................................................ 7 2.2 TE waves .................................................................................................................... 9 2.3 TM waves ................................................................................................................. 14 3 TE modes in metallic waveguides ................................................................................... 14 3.1 TE modes in a parallel-plate waveguide .................................................................. 14 3.1.1 Mathematical analysis ...................................................................................... 15 3.1.2 Physical interpretation ..................................................................................... 17 3.1.3 Velocities ......................................................................................................... 19 3.1.4 Fields ................................................................................................................ 21 3.2 TE modes in rectangular waveguides .....................................................................
    [Show full text]
  • Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
    Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels.
    [Show full text]
  • A Rack-Mounted Precision Waveguide-Below-Cutoff Attenuator with an Absolute Electronic Readout
    NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 Certain commerical equipment and materials are identified on the drawings in order to adequately specify the fabrication procedure. In no case does such identification imply recommendation or endorse- ment by the National Bureau of Standards, nor does it imply that the material or equipment identified is necessarily the best available for the purpose. November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 u s DEPARTMENT OF COMMERCE, Frederick B. Dent. Secretary NATIONAL BUREAU OF STANDARDS Richard W Roberts Director CONTENTS Page ABSTRACT 1 1. INTRODUCTION 1 2. THEORY OF OPERATION 1 3. DESCRIPTION OF ATTENUATOR 3 4. ATTENUATOR OPERATION 7 4.1 Preliminary Setup and Check 7 4.2 Displacement Readouts and Attenuation Value 7 5. OPERATIONAL CONSIDERATIONS 9 5.1 Initial Alignment 9 . 5.2 Operation 10 6. ERROR ANALYSIS , . 11 6.1 Waveguide Diameter 11 6.2 Waveguide Conductivity .... 12 6.3 Attenuation Rate 12 6.4 Displacement Readout 13 6.5 Miscellaneous Sources of Error 13 6.6 Temperature Effects . 15 6.7 Summary of Errors 16 7. SUMMARY 16 8. ACKNOWLEDGMENTS 17 9. REFERENCES 17 10. PARTS LIST 18 iii LIST OF FIGURES Page 1.
    [Show full text]
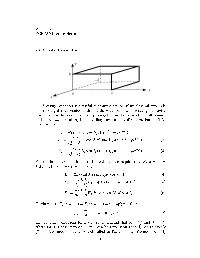
  • 23. Cavity Resonator
    WCChew ECE Lecture Notes Cavity Resonator y b –d x 0 a z A cavity resonator is a useful microwave device If we close o two ends of a rectangular waveguide with metallic walls we have a rectangular cavity resonator In this case the wave propagating in the zdirection will b ounce o the twowalls resulting in a standing waveinthezdirection For the TM casewe have j z j z z z E E sin x sin y e e z x y j x z j z j z z z E cos x sin y e e E x y x y x j y z j z j z z z E E sin x cos y e e y x y y x For the b oundary conditions to be satised we require that E z x E z Hence and y E E sin xsin y cos z z x y z x z E E cos x sin y sin z x x y z x y y z E E sin x cos y sin z y x y z x y Furthermore E z dE z d implying that x y p p z d m n The guidance conditions for a waveguide demand that and x y a b where for TM case neither m or n can be zero Now that has to satisfy z the TM mo de in a cavity is classied as TM mo de We note from mnp that p can be zero while E Hence the TM cavity mo de can exist z mn In order for and to b e solutions to the wave equation we require that m n p x y z a b d For a given choice of m n and p only a single frequency can satisfy This frequency is the resonant frequency of the cavity It is only at this frequency that the cavity can sustain a free oscillation At other frequencies the elds interfere destructively and the free oscillation is not sustained From we gather that the resonant frequency for the TM
    [Show full text]