DOCSLIB.ORG

Abnormal Radiation Pattern of Metamaterial Waveguide

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Abnormal Radiation Pattern of Metamaterial Waveguide PIERS ONLINE, VOL. 4, NO. 6, 2008 641 Abnormal Radiation Pattern of Metamaterial Waveguide A. N. Lagarkov, V. N. Semenenko, A. A. Basharin, and N. P. Balabukha Institute for Theoretical and Applied Electromagnetics of Russian Academy of Sciences (ITAE RAS) Izhorskaya 13, Moscow 125412, Russia Abstract| The idea to inverse the radiation pattern of the microwave antenna due to appli- cation of the isotropic metamaterial screen with negative refractive index in S band is demon- strated at the ¯rst time in this investigation. The electromagnetic simulation of waveguide antenna patterns by moment's methods demonstrates an agreement modeling antenna patterns with measured antenna diagrams for values of metamaterial e®ective parameters (permittivity and permeability) extracted from measured S-parameters of metamaterial sheet sample. 1. INTRODUCTION The prediction of left handed materials (LHM) by V. G. Veselago in 1967 [1] can be considered as a new stage in the development of electromagnetics of continuous media. Recently a lot of papers [2, 3] related to the arti¯cial magnetoelectric media with anomalous electromagnetic properties have been appeared. Among these papers there are ones on 2-D, 3-D media with the negative permittivity and permeability [4, 5] and, hence, negative refractive index. The abnormal antenna patterns of a rectangular open waveguide loaded by a rectangular cross-section magnetoelectric tube made of the metamaterial with the negative refractive index in S frequency band for di®erent thicknesses of tube are demonstrated at ¯rst in this paper. 2. SCHEME OF WAVEGUIDE RADIATOR The geometry of open waveguide loaded by the metamaterial screen having a shape of a rectangular cross-section tube (modi¯ed open waveguide radiator) is shown in Figs. 1{2. A standard coaxial-waveguide adapter of the S-band with the waveguide window of 50 £ 25 mm in sizes is used in the measurements of antenna patterns of modi¯ed waveguide radiator. metamaterial 0 180 0 0 feedline waveguide Figure 1: Schematic diagram of the waveguide radi- Figure 2: A view of the waveguide radiator. ation structure. The metamaterial under investigation is an isotropic 2D lattice made of nichrome spiral wires (helixes) positioned randomly on the polyurethane substrate with 0.2 mm in thickness. To exclude chiral properties of the metamaterial sample is used an identical combination of left- and right handed helixes. The helixes were wound of the 0.4 mm nichrome wire with the number of turns 3 and coil pitch 1 mm. The helix external diameter is 5 mm. In the experiments an isotropic metamaterial sheet sample named as LR-5I (see Fig. 3 | 1/3 part of helixes set is positioned along rectangular coordinate axes of x, y and z respectively) with 5.2 mm in thickness is used. PIERS ONLINE, VOL. 4, NO. 6, 2008 642 A peculiarity of the spiral elements of the metamaterial under investigation consists in revealing of the 3D-isotropic electric and magnetic properties in one and the same frequency band [4]. A helix with the non-zero coil pitch is magnetic and electric dipole simultaneously e®ectively excited both by the electric and magnetic ¯elds under the coincidence of their polarization with the helix axis. 40 30 LR-5I 20 10 0 -10 -20 -30 Phase of Transmission Coefficient, deg -40 2 2.5 3 3.5 4 Frequency, GHz Figure 3: A view of the metamaterial planar sample Figure 4: Phase of the metamaterial transmission LR-5I. coe±cient in dependence on frequency. The experimental dependence of the phase of metamaterial transmission coe±cient in the de- pendence of frequency with the area of negative values of phase in the vicinity of frequency of 3 GHz corresponding to the negative refractive index is demonstrated in Fig. 4. Extracting values of e®ective material parameters of the metamaterial sheet sample recalculated by the Fresnel's formulae from the S-parameters values (complex reflection and transmission coe±cients) are pre- sented in Fig. 5. The measurements of metamaterial S-parameters are performed on R&S Vector Network Analyzer ZVA-24 with the time domain option and special calibration procedure and using wide-band horn antenna. 9 4.0 8 ε' 3.5 7 ε'' 3.0 µ' 6 2.5 µ'' 5 2.0 4 1.5 3 1.0 2 0.5 1 0.0 0 -0.5 -1 -1.0 -2 -1.5 2.02.5 3.03.5 4.0 2.02.5 3.03.5 4.0 Frequency, GHz Frequency, GH z Figure 5: The e®ective permittivity and permeability of metamaterial LR-5I in dependence on frequency. 3. THE ANTENNA PATTERNS OF WAVEGUIDE RADIATOR LOADED BY METAMATERIAL Based upon the numerical estimations of antenna patterns by the Method of moments (thin red lines) and experimental antenna patterns (thick black lines) for the waveguide radiator obtained in the anechoic chamber are presented in Figs. 6{11. The antenna diagrams are performed at the PIERS ONLINE, VOL. 4, NO. 6, 2008 643 frequencies closed to the metamaterial resonance frequency which is equal to 3 GHz. An oppor- tunity of obtaining a reversed antenna patterns for waveguide antenna structure loaded by the metamaterial tube had been shown at these diagrams (in Figs. 6{11 normalized antenna patterns is represented). 0 0 0 0 330 30 330 30 -5 -5 -10 -10 300 60 300 60 -15 -15 -20 -25 -20 270 90 270 90 -25 -15 -20 -15 -10 240 120 240 120 -10 -5 -5 210 150 210 150 0 0 180 180 Figure 6: The antenna patterns of a waveguide ra- Figure 7: The antenna patterns of a waveguide ra- diator at the frequency 3.1 GHz. diator loaded by the metamaterial tube (d = 5 mm) at the frequency 3.1 GHz. 0 0 0 0 30 330 30 330 -5 -5 10 10 300 60 15 300 60 15 20 20 25 30 25 270 90 270 90 30 20 25 15 20 240 120 120 10 15 240 10 -5 -5 210 150 150 0 0 210 180 180 Figure 8: The antenna patterns of a waveguide radi- Figure 9: The antenna patterns of a waveguide radi- ator loaded by the metamaterial tube (d = 10 mm) ator loaded by the metamaterial tube (d = 20 mm) at the frequency 3.1 GHz. at the frequency 3.1 GHz. For a waveguide radiator loaded by the LR-5I metamaterial tube with the wall thickness d = 5 mm and length L = 150 mm there is a growing of the backside antenna lobe in comparison with the main antenna lobe. The di®erence between levels of the main and back directional lobes is approximately equal to 2 dB. With the increasing of the tube wall thickness d, there is an abnormal antenna pattern diagram when the backside directional lobe exceeds the main one more than by 20 dB. In this case the waveg- uide structure radiates mainly in the backside direction of \180 deg". This e®ectp is observed only in the case when the metamaterial reveals negative refractive index of n = ("0 + i"00)(¹0 + i¹00). To prove this fact in Fig. 11 an antenna pattern of the waveguide structure with the metamaterial PIERS ONLINE, VOL. 4, NO. 6, 2008 644 tube screen at the frequency of 4 GHz is presented. At this frequency refractive index of meta- material is n > 0. The antenna pattern at this frequency has an ordinary form of diagram where the main directional lobe exceeds the backside lobe and the radiation occurs mainly in the front direction \0 deg". The physical nature of this e®ect may be explained by the refraction of the electromagnetic waves at the boundary (air/metamaterial tube) inside waveguide structure. At this boundary the surface waves are excited and propagated in an opposite direction towards the spatial wave propagation in the waveguide structure. 0 0 0 0 330 30 330 30 -5 -5 -10 -10 -15 60 60 -20 300 -15 300 -25 -20 -30 -35 -25 -40 270 90 -30 270 90 -35 -25 -30 -25 -20 -20 -15 - 240 120 240 120 15 -10 -10 -5 -5 210 150 210 150 0 0 180 180 Figure 10: The antenna patterns of a waveguide ra- Figure 11: The antenna patterns of a waveguide ra- diator loaded by the metamaterial tube (d = 30 mm) diator loaded by the metamaterial tube (d = 20 mm) at the frequency 3.1 GHz. at the frequency 4 GHz. 4. CONCLUSIONS Therefore, at the frequencies, at which a metamaterial possess negative refractive index n < 0, and the metamaterial tube thickness exceed 5 mm, and abnormal antenna pattern diagram of waveguide structure with the maximal radiation in the backside direction (<<backside radiation>>) are observed. At the frequencies, at which n > 0, the antenna patterns present ordinary diagrams with the maximal radiation in the front direction for any metamaterial tube thickness. REFERENCES 1. Veselago, V. G., \The electrodynamics of substances with simultaneously negative values of " and ¹," Sov. Phys. Usp., Vol. 10, 509{514, 1968. 2. Caloz, C. and T. Itoh, Electromagnetic Metamaterials: Transmission Line Theory and Mi- crowave Applications, John Wiley & Sons, Inc., 2006. 3. Lagarkov, A. N., V. N. Semenenko, D. E. Ryabov, S. A. Tretyakov, and C. R. Simovski, \Resonance properties of bi-helix media at microwaves," Electromagnetics, Vol. 17, No. 3, 213{237, 1997. 4. Lagarkov, A. N., V. N. Semenenko, V. N. Kisel, and V. A. Chistyaev, \Development and sim- ulation of microwave arti¯cial magnetic composites utilizing nonmagnetic inclusion," Journal of Magnetism and Magnetic Materials, Vol. 258{259, 161{166, 2003. 5. Lagarkov, A. N. and V. N. Kissel, \Near-perfect imaging in a focusing system based on a left-handed-material plate," Phys.
Load more

Recommended publications
  • Lecture 26 Dielectric Slab Waveguides
    Lecture 26 Dielectric Slab Waveguides In this lecture you will learn: • Dielectric slab waveguides •TE and TM guided modes in dielectric slab waveguides ECE 303 – Fall 2005 – Farhan Rana – Cornell University TE Guided Modes in Parallel-Plate Metal Waveguides r E()rr = yˆ E sin()k x e− j kz z x>0 o x x Ei Ei r r Ey k E r k i r kr i H Hi i z ε µo Hr r r ki = −kx xˆ + kzzˆ kr = kx xˆ + kzzˆ Guided TE modes are TE-waves bouncing back and fourth between two metal plates and propagating in the z-direction ! The x-component of the wavevector can have only discrete values – its quantized m π k = where : m = 1, 2, 3, x d KK ECE 303 – Fall 2005 – Farhan Rana – Cornell University 1 Dielectric Waveguides - I Consider TE-wave undergoing total internal reflection: E i x ε1 µo r k E r i r kr H θ θ i i i z r H r ki = −kx xˆ + kzzˆ r kr = kx xˆ + kzzˆ Evanescent wave ε2 µo ε1 > ε2 r E()rr = yˆ E e− j ()−kx x +kz z + yˆ ΓE e− j (k x x +kz z) 2 2 2 x>0 i i kz + kx = ω µo ε1 Γ = 1 when θi > θc When θ i > θ c : kx = − jα x r E()rr = yˆ T E e− j kz z e−α x x 2 2 2 x<0 i kz − α x = ω µo ε2 ECE 303 – Fall 2005 – Farhan Rana – Cornell University Dielectric Waveguides - II x ε2 µo Evanescent wave cladding Ei E ε1 µo r i r k E r k i r kr i core Hi θi θi Hi ε1 > ε2 z Hr cladding Evanescent wave ε2 µo One can have a guided wave that is bouncing between two dielectric interfaces due to total internal reflection and moving in the z-direction ECE 303 – Fall 2005 – Farhan Rana – Cornell University 2 Dielectric Slab Waveguides W 2d Assumption: W >> d x cladding y core
    [Show full text]
  • High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium
    Progress In Electromagnetics Research C, Vol. 79, 115–126, 2017 High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium Adel A. A. Abdelrehim and Hooshang Ghafouri-Shiraz* Abstract—In this paper, a new high performance slotted waveguide antenna incorporated with negative refractive index metamaterial structure is proposed, designed and experimentally demonstrated. The metamaterial structure is constructed from a multilayer two-directional structure of electrically split ring resonator which exhibits negative refractive index in direction of the radiated wave propagation when it is placed in front of the slotted waveguide antenna. As a result, the radiation beams of the slotted waveguide antenna are focused in both E and H planes, and hence the directivity and the gain are improved, while the beam area is reduced. The proposed antenna and the metamaterial structure operating at 10 GHz are designed, optimized and numerically simulated by using CST software. The effective parameters of the eSRR structure are extracted by Nicolson Ross Weir (NRW) algorithm from the s-parameters. For experimental verification, a proposed antenna operating at 10 GHz is fabricated using both wet etching microwave integrated circuit technique (for the metamaterial structure) and milling technique (for the slotted waveguide antenna). The measurements are carried out in an anechoic chamber. The measured results show that the E plane gain of the proposed slotted waveguide antenna is improved from 6.5 dB to 11 dB as compared to the conventional slotted waveguide antenna. Also, the E plane beamwidth is reduced from 94.1 degrees to about 50 degrees.
    [Show full text]
  • Waveguide Direction User Manual
    WaveGuide Direction Ex. Certified User Manual WaveGuide Direction Ex. Certified User Manual Applicable for product no. WG-DR40-EX Related to software versions: wdr 4.#-# Version 4.0 21st of November 2016 Radac B.V. Elektronicaweg 16b 2628 XG Delft The Netherlands tel: +31(0)15 890 3203 e-mail: [email protected] website: www.radac.nl Preface This user manual and technical documentation is intended for engineers and technicians involved in the software and hardware setup of the Ex. certified version of the WaveGuide Direction. Note All connections to the instrument must be made with shielded cables with exception of the mains. The shielding must be grounded in the cable gland or in the terminal compartment on both ends of the cable. For more information regarding wiring and cable specifications, please refer to Chapter 2. Legal aspects The mechanical and electrical installation shall only be carried out by trained personnel with knowledge of the local requirements and regulations for installation of electronic equipment. The information in this installation guide is the copyright property of Radac BV. Radac BV disclaims any responsibility for personal injury or damage to equipment caused by: Deviation from any of the prescribed procedures. • Execution of activities that are not prescribed. • Neglect of the general safety precautions for handling tools and use of electricity. • The contents, descriptions and specifications in this installation guide are subject to change without notice. Radac BV accepts no responsibility for any errors that may appear in this user manual. Additional information Please do not hesitate to contact Radac or its representative if you require additional information.
    [Show full text]
  • Instruction Manual Waveguide & Waveguide Server
    Instruction manual WaveGuide & WaveGuide Server Radac bv Elektronicaweg 16b 2628 XG DELFT Phone: +31 15 890 32 03 Email: [email protected] www.radac.n l Instruction manual WaveGuide + WaveGuide Server Version 4.1 2 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Version 4.1 3 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Table of Contents Introduction...................................................................................................................................................................4 Installation.....................................................................................................................................................................5 The WaveGuide Sensor...........................................................................................................................................5 CaBling.....................................................................................................................................................................6 The WaveGuide Server............................................................................................................................................7 Commissioning the system...........................................................................................................................................9 Connect the WGS to a computer.............................................................................................................................9 Authorization.........................................................................................................................................................10
    [Show full text]
  • Analysis of a Waveguide-Fed Metasurface Antenna
    Analysis of a Waveguide-Fed Metasurface Antenna Smith, D., Yurduseven, O., Mancera, L. P., Bowen, P., & Kundtz, N. B. (2017). Analysis of a Waveguide-Fed Metasurface Antenna. Physical Review Applied, 8(5). https://doi.org/10.1103/PhysRevApplied.8.054048 Published in: Physical Review Applied Document Version: Publisher's PDF, also known as Version of record Queen's University Belfast - Research Portal: Link to publication record in Queen's University Belfast Research Portal Publisher rights © 2017 American Physical Society. This work is made available online in accordance with the publisher’s policies. Please refer to any applicable terms of use of the publisher. General rights Copyright for the publications made accessible via the Queen's University Belfast Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy The Research Portal is Queen's institutional repository that provides access to Queen's research output. Every effort has been made to ensure that content in the Research Portal does not infringe any person's rights, or applicable UK laws. If you discover content in the Research Portal that you believe breaches copyright or violates any law, please contact [email protected]. Download date:02. Oct. 2021 PHYSICAL REVIEW APPLIED 8, 054048 (2017) Analysis of a Waveguide-Fed Metasurface Antenna † † David R. Smith,* Okan Yurduseven, Laura Pulido Mancera, and Patrick Bowen Department of Electrical and Computer Engineering, Duke University, Durham, North Carolina 27708, USA Nathan B.
    [Show full text]
  • Waveguide Propagation
    NTNU Institutt for elektronikk og telekommunikasjon Januar 2006 Waveguide propagation Helge Engan Contents 1 Introduction ........................................................................................................................ 2 2 Propagation in waveguides, general relations .................................................................... 2 2.1 TEM waves ................................................................................................................ 7 2.2 TE waves .................................................................................................................... 9 2.3 TM waves ................................................................................................................. 14 3 TE modes in metallic waveguides ................................................................................... 14 3.1 TE modes in a parallel-plate waveguide .................................................................. 14 3.1.1 Mathematical analysis ...................................................................................... 15 3.1.2 Physical interpretation ..................................................................................... 17 3.1.3 Velocities ......................................................................................................... 19 3.1.4 Fields ................................................................................................................ 21 3.2 TE modes in rectangular waveguides .....................................................................
    [Show full text]
  • Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
    Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels.
    [Show full text]
  • A Rack-Mounted Precision Waveguide-Below-Cutoff Attenuator with an Absolute Electronic Readout
    NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 Certain commerical equipment and materials are identified on the drawings in order to adequately specify the fabrication procedure. In no case does such identification imply recommendation or endorse- ment by the National Bureau of Standards, nor does it imply that the material or equipment identified is necessarily the best available for the purpose. November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 u s DEPARTMENT OF COMMERCE, Frederick B. Dent. Secretary NATIONAL BUREAU OF STANDARDS Richard W Roberts Director CONTENTS Page ABSTRACT 1 1. INTRODUCTION 1 2. THEORY OF OPERATION 1 3. DESCRIPTION OF ATTENUATOR 3 4. ATTENUATOR OPERATION 7 4.1 Preliminary Setup and Check 7 4.2 Displacement Readouts and Attenuation Value 7 5. OPERATIONAL CONSIDERATIONS 9 5.1 Initial Alignment 9 . 5.2 Operation 10 6. ERROR ANALYSIS , . 11 6.1 Waveguide Diameter 11 6.2 Waveguide Conductivity .... 12 6.3 Attenuation Rate 12 6.4 Displacement Readout 13 6.5 Miscellaneous Sources of Error 13 6.6 Temperature Effects . 15 6.7 Summary of Errors 16 7. SUMMARY 16 8. ACKNOWLEDGMENTS 17 9. REFERENCES 17 10. PARTS LIST 18 iii LIST OF FIGURES Page 1.
    [Show full text]
  • 23. Cavity Resonator
    WCChew ECE Lecture Notes Cavity Resonator y b –d x 0 a z A cavity resonator is a useful microwave device If we close o two ends of a rectangular waveguide with metallic walls we have a rectangular cavity resonator In this case the wave propagating in the zdirection will b ounce o the twowalls resulting in a standing waveinthezdirection For the TM casewe have j z j z z z E E sin x sin y e e z x y j x z j z j z z z E cos x sin y e e E x y x y x j y z j z j z z z E E sin x cos y e e y x y y x For the b oundary conditions to be satised we require that E z x E z Hence and y E E sin xsin y cos z z x y z x z E E cos x sin y sin z x x y z x y y z E E sin x cos y sin z y x y z x y Furthermore E z dE z d implying that x y p p z d m n The guidance conditions for a waveguide demand that and x y a b where for TM case neither m or n can be zero Now that has to satisfy z the TM mo de in a cavity is classied as TM mo de We note from mnp that p can be zero while E Hence the TM cavity mo de can exist z mn In order for and to b e solutions to the wave equation we require that m n p x y z a b d For a given choice of m n and p only a single frequency can satisfy This frequency is the resonant frequency of the cavity It is only at this frequency that the cavity can sustain a free oscillation At other frequencies the elds interfere destructively and the free oscillation is not sustained From we gather that the resonant frequency for the TM
    [Show full text]
  • Design of Slotted Waveguide Antenna for Radar Applications at X-Band
    International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 3 Issue 11, November-2014 Design of Slotted Waveguide Antenna for Radar Applications at X-Band S. Murugaveni1 T. Karthick 2 1Assistant Professor, M.Tech, 2 Department of Telecommunication Engineering, Department of Telecommunication Engineering, SRM University, Kattankulathur – 603203, SRM University, Kattankulathur – 603203, Chennai, India. Chennai,India. Abstract --A slotted waveguide antenna has been designed for I MATHEMATICAL MODELING radar applications at X-band, 9.47 GHz. Slotted waveguide The dominant mode in a rectangular waveguide with antennas are mostly employed in Radar applications. This dimension a > b is the TE10 mode. Dominant mode is paper analysis the structure and design procedures of slotted always a low loss, distortion less transmission and higher antenna in the broad wall. This design specifications are modes result in significant loss of power and also chosen for high gain and mechanical robustness. The slotted waveguide antenna designed is a directional type antenna undesirable harmonic distortion. The standard length of the with gain of 16db. We first obtain the physical size of each slot wave guide is shown in the figure where the slot length is by using parameter sweep function Ansoft High Frequency around half of the wavelength over the air,휆 2. The slots Structured Simulation (HFSS) software. Then we created a are milled onto a standard waveguide wr90 with inner complete model. Finally we perform the simulation and waveguide dimension of 22.86 × 10.16 mm arranged in compare against the design requirement. There is a good two vertical columns offset from the centre which acts as agreement between simulation and design requirement.
    [Show full text]
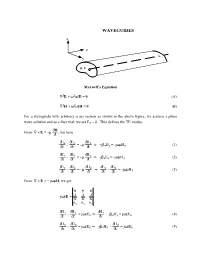
  • WAVEGUIDES X
    WAVEGUIDES x z y µ, ε Maxwell's Equation ∇2E + ω2µεE = 0 (A) ∇2H + ω2µεH = 0 (B) For a waveguide with arbitrary cross section as shown in the above figure, we assume a plane wave solution and as a first trial, we set Ez = 0. This defines the TE modes. ∂H ∇ × = −µ , we have From E ∂t ∂ ∂ ∂ Ez Ey µ Hx ⇒ β ωµ ∂y - ∂z = - ∂t +j zEy = -j Hx (1) ∂ ∂ ∂ Ex Ez µ Hy ⇒ β ωµ ∂z - ∂x = - ∂t -j zEx = -j Hy (2) ∂ ∂ ∂ ∂ ∂ Ey Ex µ Hz ⇒ Ey Ex ωµ ∂x - ∂y = - ∂t ∂x - ∂y = -j Hz (3) From ∇ × E = − jωµH, we get xyzˆˆˆ ∂ ∂ ∂ jωεE = ∂xxz∂ ∂ Hx Hy Hz ∂ ∂ ∂ Hz Hy ωε ⇒ Hz β ωε ∂y - ∂z = j Ex ∂y + j zHy = j Ex (4) ∂ ∂ ∂ Hx Hz ωε ⇒ β Hz ωε ∂z - ∂x = j Ey -j zHx - ∂x = j Ey (5) - 2 - ∂Hy ∂Hx ∂x - ∂y = 0 (6) We want to express all quantities in terms of Hz. From (2), we have β E H = z x (7) y ωµ in (4) ∂H E z + jβ 2 x = jωεE (8) ∂y z ωµ x Solving for Ex jωµ ∂Hz Ex = ∂y (9) βz2-ω2µε From (1) -β E H = z y (10) x ωµ in (5) β 2E ∂Hz +j z y - = jωεE (11) ωµ ∂x y so that -jωµ ∂Hz Ey = ∂x (12) βz2-ω2µε jβz ∂Hz Hx = ∂x (13) βz2-ω2µε jβz ∂Hz Hy = ∂y (14) βz2-ω2µε Ez = 0 (15) - 3 - Combining solutions for Ex and Ey into (3) gives ∂2Hz ∂2Hz + = [βz2-ω2µε]Hz (16) ∂x2 ∂y2 RECTANGULAR WAVEGUIDES y x z µ, ε b a If the cross section of the waveguide is a rectangle, we have a rectangular waveguide and the boundary conditions are such that the tangential electric field is zero on all the PEC walls.
    [Show full text]
  • Planar Transmission Lines
    Adapted from notes by ECE 5317-6351 Prof. Jeffery T. Williams Microwave Engineering Fall 2018 Prof. David R. Jackson Dept. of ECE Notes 11 Waveguiding Structures Part 6: Planar Transmission Lines w ε0 ε r h 1 Planar Transmission Lines w w b ε h r εr Microstrip Stripline w w εr g g h εr g g h Coplanar Waveguide (CPW) Conductor-backed CPW s s εr h εr h Slotline Conductor-backed Slotline 2 Planar Transmission Lines (cont.) w w w w ε h εr s h r s Coplanar Strips (CPS) Conductor-backed CPS . Stripline is a planar version of coax. Coplanar strips (CPS) is a planar version of twin lead. 3 Stripline . Common on circuit boards ε,, µσd b . Fabricated with two circuit boards w . Homogenous dielectric (perfect TEM mode) TEM mode (also TE & TM Modes) Field structure for TEM mode: Electric Field Magnetic Field 4 Stripline (cont.) . Analysis of stripline is not simple. TEM mode fields can be obtained from an electrostatic analysis (e.g., conformal mapping). A closed stripline structure is analyzed in the Pozar book by using an approximate numerical method: b w b /2 ε,, µσd a ab>> 5 Stripline (cont.) Conformal mapping solution (S. Cohn): Exact solution: 30π Kk ( ) Z0 = K = complete elliptic Kk()′ integral of the first kind π /2 1 Kk( ) ≡ dθ ∫ 22 0 1− k sin θ π w k = sech 2b π w k′ = tanh 2b 6 Stripline (cont.) Curve fitting this exact solution: η b Z = 0 ln( 4) 0 ε ln(4) Note : = 0.441 4 r wb+ π e π Effective width Fringing term w 0 ;for ≥ 0.35 wwe b = − 2 bbww 0.35− ;for 0.1≤≤ 0.35 bb 1bb /2 η η b ideal 0 The factor of 1/2 in front is from the parallel Note: Z0 =η = = 24ww4w ε r combination of two ideal PPWs.
    [Show full text]