High Gain Slotted Waveguide Antenna Based on Beam Focusing Using Electrically Split Ring Resonator Metasurface Employing Negative Refractive Index Medium
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lecture 26 Dielectric Slab Waveguides
Lecture 26 Dielectric Slab Waveguides In this lecture you will learn: • Dielectric slab waveguides •TE and TM guided modes in dielectric slab waveguides ECE 303 – Fall 2005 – Farhan Rana – Cornell University TE Guided Modes in Parallel-Plate Metal Waveguides r E()rr = yˆ E sin()k x e− j kz z x>0 o x x Ei Ei r r Ey k E r k i r kr i H Hi i z ε µo Hr r r ki = −kx xˆ + kzzˆ kr = kx xˆ + kzzˆ Guided TE modes are TE-waves bouncing back and fourth between two metal plates and propagating in the z-direction ! The x-component of the wavevector can have only discrete values – its quantized m π k = where : m = 1, 2, 3, x d KK ECE 303 – Fall 2005 – Farhan Rana – Cornell University 1 Dielectric Waveguides - I Consider TE-wave undergoing total internal reflection: E i x ε1 µo r k E r i r kr H θ θ i i i z r H r ki = −kx xˆ + kzzˆ r kr = kx xˆ + kzzˆ Evanescent wave ε2 µo ε1 > ε2 r E()rr = yˆ E e− j ()−kx x +kz z + yˆ ΓE e− j (k x x +kz z) 2 2 2 x>0 i i kz + kx = ω µo ε1 Γ = 1 when θi > θc When θ i > θ c : kx = − jα x r E()rr = yˆ T E e− j kz z e−α x x 2 2 2 x<0 i kz − α x = ω µo ε2 ECE 303 – Fall 2005 – Farhan Rana – Cornell University Dielectric Waveguides - II x ε2 µo Evanescent wave cladding Ei E ε1 µo r i r k E r k i r kr i core Hi θi θi Hi ε1 > ε2 z Hr cladding Evanescent wave ε2 µo One can have a guided wave that is bouncing between two dielectric interfaces due to total internal reflection and moving in the z-direction ECE 303 – Fall 2005 – Farhan Rana – Cornell University 2 Dielectric Slab Waveguides W 2d Assumption: W >> d x cladding y core -

Waveguide Direction User Manual
WaveGuide Direction Ex. Certified User Manual WaveGuide Direction Ex. Certified User Manual Applicable for product no. WG-DR40-EX Related to software versions: wdr 4.#-# Version 4.0 21st of November 2016 Radac B.V. Elektronicaweg 16b 2628 XG Delft The Netherlands tel: +31(0)15 890 3203 e-mail: [email protected] website: www.radac.nl Preface This user manual and technical documentation is intended for engineers and technicians involved in the software and hardware setup of the Ex. certified version of the WaveGuide Direction. Note All connections to the instrument must be made with shielded cables with exception of the mains. The shielding must be grounded in the cable gland or in the terminal compartment on both ends of the cable. For more information regarding wiring and cable specifications, please refer to Chapter 2. Legal aspects The mechanical and electrical installation shall only be carried out by trained personnel with knowledge of the local requirements and regulations for installation of electronic equipment. The information in this installation guide is the copyright property of Radac BV. Radac BV disclaims any responsibility for personal injury or damage to equipment caused by: Deviation from any of the prescribed procedures. • Execution of activities that are not prescribed. • Neglect of the general safety precautions for handling tools and use of electricity. • The contents, descriptions and specifications in this installation guide are subject to change without notice. Radac BV accepts no responsibility for any errors that may appear in this user manual. Additional information Please do not hesitate to contact Radac or its representative if you require additional information. -

Instruction Manual Waveguide & Waveguide Server
Instruction manual WaveGuide & WaveGuide Server Radac bv Elektronicaweg 16b 2628 XG DELFT Phone: +31 15 890 32 03 Email: [email protected] www.radac.n l Instruction manual WaveGuide + WaveGuide Server Version 4.1 2 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Version 4.1 3 of 30 Oct 2013 Instruction manual WaveGuide + WaveGuide Server Table of Contents Introduction...................................................................................................................................................................4 Installation.....................................................................................................................................................................5 The WaveGuide Sensor...........................................................................................................................................5 CaBling.....................................................................................................................................................................6 The WaveGuide Server............................................................................................................................................7 Commissioning the system...........................................................................................................................................9 Connect the WGS to a computer.............................................................................................................................9 Authorization.........................................................................................................................................................10 -

Analysis of a Waveguide-Fed Metasurface Antenna
Analysis of a Waveguide-Fed Metasurface Antenna Smith, D., Yurduseven, O., Mancera, L. P., Bowen, P., & Kundtz, N. B. (2017). Analysis of a Waveguide-Fed Metasurface Antenna. Physical Review Applied, 8(5). https://doi.org/10.1103/PhysRevApplied.8.054048 Published in: Physical Review Applied Document Version: Publisher's PDF, also known as Version of record Queen's University Belfast - Research Portal: Link to publication record in Queen's University Belfast Research Portal Publisher rights © 2017 American Physical Society. This work is made available online in accordance with the publisher’s policies. Please refer to any applicable terms of use of the publisher. General rights Copyright for the publications made accessible via the Queen's University Belfast Research Portal is retained by the author(s) and / or other copyright owners and it is a condition of accessing these publications that users recognise and abide by the legal requirements associated with these rights. Take down policy The Research Portal is Queen's institutional repository that provides access to Queen's research output. Every effort has been made to ensure that content in the Research Portal does not infringe any person's rights, or applicable UK laws. If you discover content in the Research Portal that you believe breaches copyright or violates any law, please contact [email protected]. Download date:02. Oct. 2021 PHYSICAL REVIEW APPLIED 8, 054048 (2017) Analysis of a Waveguide-Fed Metasurface Antenna † † David R. Smith,* Okan Yurduseven, Laura Pulido Mancera, and Patrick Bowen Department of Electrical and Computer Engineering, Duke University, Durham, North Carolina 27708, USA Nathan B. -

Waveguide Propagation
NTNU Institutt for elektronikk og telekommunikasjon Januar 2006 Waveguide propagation Helge Engan Contents 1 Introduction ........................................................................................................................ 2 2 Propagation in waveguides, general relations .................................................................... 2 2.1 TEM waves ................................................................................................................ 7 2.2 TE waves .................................................................................................................... 9 2.3 TM waves ................................................................................................................. 14 3 TE modes in metallic waveguides ................................................................................... 14 3.1 TE modes in a parallel-plate waveguide .................................................................. 14 3.1.1 Mathematical analysis ...................................................................................... 15 3.1.2 Physical interpretation ..................................................................................... 17 3.1.3 Velocities ......................................................................................................... 19 3.1.4 Fields ................................................................................................................ 21 3.2 TE modes in rectangular waveguides ..................................................................... -

Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels. -

A Rack-Mounted Precision Waveguide-Below-Cutoff Attenuator with an Absolute Electronic Readout
NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 NBSIR 74-394 A RACK-MOUNTED PRECISION WAVEGUIDE-BELOW-CUTOFF ATTENUATOR WITH AN ABSOLUTE ELECTRONIC READOUT Clarence C. Cook Electromagnetics Division Institute for Basic Standards National Bureau of Standards Boulder, Colorado 80302 Certain commerical equipment and materials are identified on the drawings in order to adequately specify the fabrication procedure. In no case does such identification imply recommendation or endorse- ment by the National Bureau of Standards, nor does it imply that the material or equipment identified is necessarily the best available for the purpose. November 1974 Prepared for Jet Propulsion Laboratory Pasadena, California 91103 u s DEPARTMENT OF COMMERCE, Frederick B. Dent. Secretary NATIONAL BUREAU OF STANDARDS Richard W Roberts Director CONTENTS Page ABSTRACT 1 1. INTRODUCTION 1 2. THEORY OF OPERATION 1 3. DESCRIPTION OF ATTENUATOR 3 4. ATTENUATOR OPERATION 7 4.1 Preliminary Setup and Check 7 4.2 Displacement Readouts and Attenuation Value 7 5. OPERATIONAL CONSIDERATIONS 9 5.1 Initial Alignment 9 . 5.2 Operation 10 6. ERROR ANALYSIS , . 11 6.1 Waveguide Diameter 11 6.2 Waveguide Conductivity .... 12 6.3 Attenuation Rate 12 6.4 Displacement Readout 13 6.5 Miscellaneous Sources of Error 13 6.6 Temperature Effects . 15 6.7 Summary of Errors 16 7. SUMMARY 16 8. ACKNOWLEDGMENTS 17 9. REFERENCES 17 10. PARTS LIST 18 iii LIST OF FIGURES Page 1. -
23. Cavity Resonator
WCChew ECE Lecture Notes Cavity Resonator y b –d x 0 a z A cavity resonator is a useful microwave device If we close o two ends of a rectangular waveguide with metallic walls we have a rectangular cavity resonator In this case the wave propagating in the zdirection will b ounce o the twowalls resulting in a standing waveinthezdirection For the TM casewe have j z j z z z E E sin x sin y e e z x y j x z j z j z z z E cos x sin y e e E x y x y x j y z j z j z z z E E sin x cos y e e y x y y x For the b oundary conditions to be satised we require that E z x E z Hence and y E E sin xsin y cos z z x y z x z E E cos x sin y sin z x x y z x y y z E E sin x cos y sin z y x y z x y Furthermore E z dE z d implying that x y p p z d m n The guidance conditions for a waveguide demand that and x y a b where for TM case neither m or n can be zero Now that has to satisfy z the TM mo de in a cavity is classied as TM mo de We note from mnp that p can be zero while E Hence the TM cavity mo de can exist z mn In order for and to b e solutions to the wave equation we require that m n p x y z a b d For a given choice of m n and p only a single frequency can satisfy This frequency is the resonant frequency of the cavity It is only at this frequency that the cavity can sustain a free oscillation At other frequencies the elds interfere destructively and the free oscillation is not sustained From we gather that the resonant frequency for the TM -

Design of Slotted Waveguide Antenna for Radar Applications at X-Band
International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 3 Issue 11, November-2014 Design of Slotted Waveguide Antenna for Radar Applications at X-Band S. Murugaveni1 T. Karthick 2 1Assistant Professor, M.Tech, 2 Department of Telecommunication Engineering, Department of Telecommunication Engineering, SRM University, Kattankulathur – 603203, SRM University, Kattankulathur – 603203, Chennai, India. Chennai,India. Abstract --A slotted waveguide antenna has been designed for I MATHEMATICAL MODELING radar applications at X-band, 9.47 GHz. Slotted waveguide The dominant mode in a rectangular waveguide with antennas are mostly employed in Radar applications. This dimension a > b is the TE10 mode. Dominant mode is paper analysis the structure and design procedures of slotted always a low loss, distortion less transmission and higher antenna in the broad wall. This design specifications are modes result in significant loss of power and also chosen for high gain and mechanical robustness. The slotted waveguide antenna designed is a directional type antenna undesirable harmonic distortion. The standard length of the with gain of 16db. We first obtain the physical size of each slot wave guide is shown in the figure where the slot length is by using parameter sweep function Ansoft High Frequency around half of the wavelength over the air,휆 2. The slots Structured Simulation (HFSS) software. Then we created a are milled onto a standard waveguide wr90 with inner complete model. Finally we perform the simulation and waveguide dimension of 22.86 × 10.16 mm arranged in compare against the design requirement. There is a good two vertical columns offset from the centre which acts as agreement between simulation and design requirement. -

Abnormal Radiation Pattern of Metamaterial Waveguide
PIERS ONLINE, VOL. 4, NO. 6, 2008 641 Abnormal Radiation Pattern of Metamaterial Waveguide A. N. Lagarkov, V. N. Semenenko, A. A. Basharin, and N. P. Balabukha Institute for Theoretical and Applied Electromagnetics of Russian Academy of Sciences (ITAE RAS) Izhorskaya 13, Moscow 125412, Russia Abstract| The idea to inverse the radiation pattern of the microwave antenna due to appli- cation of the isotropic metamaterial screen with negative refractive index in S band is demon- strated at the ¯rst time in this investigation. The electromagnetic simulation of waveguide antenna patterns by moment's methods demonstrates an agreement modeling antenna patterns with measured antenna diagrams for values of metamaterial e®ective parameters (permittivity and permeability) extracted from measured S-parameters of metamaterial sheet sample. 1. INTRODUCTION The prediction of left handed materials (LHM) by V. G. Veselago in 1967 [1] can be considered as a new stage in the development of electromagnetics of continuous media. Recently a lot of papers [2, 3] related to the arti¯cial magnetoelectric media with anomalous electromagnetic properties have been appeared. Among these papers there are ones on 2-D, 3-D media with the negative permittivity and permeability [4, 5] and, hence, negative refractive index. The abnormal antenna patterns of a rectangular open waveguide loaded by a rectangular cross-section magnetoelectric tube made of the metamaterial with the negative refractive index in S frequency band for di®erent thicknesses of tube are demonstrated at ¯rst in this paper. 2. SCHEME OF WAVEGUIDE RADIATOR The geometry of open waveguide loaded by the metamaterial screen having a shape of a rectangular cross-section tube (modi¯ed open waveguide radiator) is shown in Figs. -
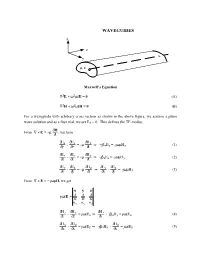
WAVEGUIDES X
WAVEGUIDES x z y µ, ε Maxwell's Equation ∇2E + ω2µεE = 0 (A) ∇2H + ω2µεH = 0 (B) For a waveguide with arbitrary cross section as shown in the above figure, we assume a plane wave solution and as a first trial, we set Ez = 0. This defines the TE modes. ∂H ∇ × = −µ , we have From E ∂t ∂ ∂ ∂ Ez Ey µ Hx ⇒ β ωµ ∂y - ∂z = - ∂t +j zEy = -j Hx (1) ∂ ∂ ∂ Ex Ez µ Hy ⇒ β ωµ ∂z - ∂x = - ∂t -j zEx = -j Hy (2) ∂ ∂ ∂ ∂ ∂ Ey Ex µ Hz ⇒ Ey Ex ωµ ∂x - ∂y = - ∂t ∂x - ∂y = -j Hz (3) From ∇ × E = − jωµH, we get xyzˆˆˆ ∂ ∂ ∂ jωεE = ∂xxz∂ ∂ Hx Hy Hz ∂ ∂ ∂ Hz Hy ωε ⇒ Hz β ωε ∂y - ∂z = j Ex ∂y + j zHy = j Ex (4) ∂ ∂ ∂ Hx Hz ωε ⇒ β Hz ωε ∂z - ∂x = j Ey -j zHx - ∂x = j Ey (5) - 2 - ∂Hy ∂Hx ∂x - ∂y = 0 (6) We want to express all quantities in terms of Hz. From (2), we have β E H = z x (7) y ωµ in (4) ∂H E z + jβ 2 x = jωεE (8) ∂y z ωµ x Solving for Ex jωµ ∂Hz Ex = ∂y (9) βz2-ω2µε From (1) -β E H = z y (10) x ωµ in (5) β 2E ∂Hz +j z y - = jωεE (11) ωµ ∂x y so that -jωµ ∂Hz Ey = ∂x (12) βz2-ω2µε jβz ∂Hz Hx = ∂x (13) βz2-ω2µε jβz ∂Hz Hy = ∂y (14) βz2-ω2µε Ez = 0 (15) - 3 - Combining solutions for Ex and Ey into (3) gives ∂2Hz ∂2Hz + = [βz2-ω2µε]Hz (16) ∂x2 ∂y2 RECTANGULAR WAVEGUIDES y x z µ, ε b a If the cross section of the waveguide is a rectangle, we have a rectangular waveguide and the boundary conditions are such that the tangential electric field is zero on all the PEC walls. -

Planar Transmission Lines
Adapted from notes by ECE 5317-6351 Prof. Jeffery T. Williams Microwave Engineering Fall 2018 Prof. David R. Jackson Dept. of ECE Notes 11 Waveguiding Structures Part 6: Planar Transmission Lines w ε0 ε r h 1 Planar Transmission Lines w w b ε h r εr Microstrip Stripline w w εr g g h εr g g h Coplanar Waveguide (CPW) Conductor-backed CPW s s εr h εr h Slotline Conductor-backed Slotline 2 Planar Transmission Lines (cont.) w w w w ε h εr s h r s Coplanar Strips (CPS) Conductor-backed CPS . Stripline is a planar version of coax. Coplanar strips (CPS) is a planar version of twin lead. 3 Stripline . Common on circuit boards ε,, µσd b . Fabricated with two circuit boards w . Homogenous dielectric (perfect TEM mode) TEM mode (also TE & TM Modes) Field structure for TEM mode: Electric Field Magnetic Field 4 Stripline (cont.) . Analysis of stripline is not simple. TEM mode fields can be obtained from an electrostatic analysis (e.g., conformal mapping). A closed stripline structure is analyzed in the Pozar book by using an approximate numerical method: b w b /2 ε,, µσd a ab>> 5 Stripline (cont.) Conformal mapping solution (S. Cohn): Exact solution: 30π Kk ( ) Z0 = K = complete elliptic Kk()′ integral of the first kind π /2 1 Kk( ) ≡ dθ ∫ 22 0 1− k sin θ π w k = sech 2b π w k′ = tanh 2b 6 Stripline (cont.) Curve fitting this exact solution: η b Z = 0 ln( 4) 0 ε ln(4) Note : = 0.441 4 r wb+ π e π Effective width Fringing term w 0 ;for ≥ 0.35 wwe b = − 2 bbww 0.35− ;for 0.1≤≤ 0.35 bb 1bb /2 η η b ideal 0 The factor of 1/2 in front is from the parallel Note: Z0 =η = = 24ww4w ε r combination of two ideal PPWs.