Graphical Law Beneath Each Written Natural Language
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Some Principles of the Use of Macro-Areas Language Dynamics &A
Online Appendix for Harald Hammarstr¨om& Mark Donohue (2014) Some Principles of the Use of Macro-Areas Language Dynamics & Change Harald Hammarstr¨om& Mark Donohue The following document lists the languages of the world and their as- signment to the macro-areas described in the main body of the paper as well as the WALS macro-area for languages featured in the WALS 2005 edi- tion. 7160 languages are included, which represent all languages for which we had coordinates available1. Every language is given with its ISO-639-3 code (if it has one) for proper identification. The mapping between WALS languages and ISO-codes was done by using the mapping downloadable from the 2011 online WALS edition2 (because a number of errors in the mapping were corrected for the 2011 edition). 38 WALS languages are not given an ISO-code in the 2011 mapping, 36 of these have been assigned their appropri- ate iso-code based on the sources the WALS lists for the respective language. This was not possible for Tasmanian (WALS-code: tsm) because the WALS mixes data from very different Tasmanian languages and for Kualan (WALS- code: kua) because no source is given. 17 WALS-languages were assigned ISO-codes which have subsequently been retired { these have been assigned their appropriate updated ISO-code. In many cases, a WALS-language is mapped to several ISO-codes. As this has no bearing for the assignment to macro-areas, multiple mappings have been retained. 1There are another couple of hundred languages which are attested but for which our database currently lacks coordinates. -

Minority Languages in India
Thomas Benedikter Minority Languages in India An appraisal of the linguistic rights of minorities in India ---------------------------- EURASIA-Net Europe-South Asia Exchange on Supranational (Regional) Policies and Instruments for the Promotion of Human Rights and the Management of Minority Issues 2 Linguistic minorities in India An appraisal of the linguistic rights of minorities in India Bozen/Bolzano, March 2013 This study was originally written for the European Academy of Bolzano/Bozen (EURAC), Institute for Minority Rights, in the frame of the project Europe-South Asia Exchange on Supranational (Regional) Policies and Instruments for the Promotion of Human Rights and the Management of Minority Issues (EURASIA-Net). The publication is based on extensive research in eight Indian States, with the support of the European Academy of Bozen/Bolzano and the Mahanirban Calcutta Research Group, Kolkata. EURASIA-Net Partners Accademia Europea Bolzano/Europäische Akademie Bozen (EURAC) – Bolzano/Bozen (Italy) Brunel University – West London (UK) Johann Wolfgang Goethe-Universität – Frankfurt am Main (Germany) Mahanirban Calcutta Research Group (India) South Asian Forum for Human Rights (Nepal) Democratic Commission of Human Development (Pakistan), and University of Dhaka (Bangladesh) Edited by © Thomas Benedikter 2013 Rights and permissions Copying and/or transmitting parts of this work without prior permission, may be a violation of applicable law. The publishers encourage dissemination of this publication and would be happy to grant permission. -

Day 1: June 8, 2016 09.00-09.03 Opening Remarks Prof
22nd Himalayan Languages Symposium June 8-10, 2016 Day 1: June 8, 2016 09.00-09.03 Opening Remarks Prof. Sukumar Nandi, Head, CLST, Indian Institute of Technology Guwahati 09.03-09.10 Welcome Address Prof. Arupjyoti Saikia, Head, HSS, Indian Institute of Technology Guwahati 09.10-09.20 Chief Guest's Address Prof. Gautam Barua, Director, Indian Institute of Information Technology Guwahati 09.20-09.25 Director’s Address Prof. Gautam Biswas, Director, Indian Institute of Technology Guwahati 09.25-09.30 Vote of thanks Dr. Bidisha Som, Dept. of HSS, Indian Institute of Technology Guwahati 09.30-09.55: Tea 09.55-10.00 Announcement of HLS 23 10.00-11.00 Speaker: Prof. George van Driem, University of Bern Keynote: The Eastern Himalayan Corridor in Prehistory Chair: Prof. Gautam Barua, Director, IIIT Guwahati HALL 1: Phonetics & Phonology HALL 2: Panel on Syntax of NE Languages Hall 3: Panel on Language and Politics Chair: Priyankoo Sarmah Coordinator: Tanmoy Bhattacharya Coordinator: Mithilesh K Jha 11.10-11.30 A1: Temsunungsang T B1: Lalit Rajkumar C1: Madhumita Sengupta Tonal correspondences in the Ao Verbal Recursion in Meiteilon Christian Missionaries and the Conversion of languages of Nagaland Language in Nineteenth-century Assam 11.30-11.50 A2: Kalyan Das B2: Alfina Khaidem C2: Trisha Wangno Tone and Intonation in Boro Syntactic Variation in Meeteilon: An Language Policy and Arunachal Pradesh Exoskeletal approach 11.50-12.10 A3: Jeremy Perkins & Seunghun Lee and B3: Gaurashyam Singh Hidam C3: Sayantani Pathak Julian Villegas Space and Tense -

The Naga Language Groups Within the Tibeto-Burman Language Family
TheNaga Language Groups within the Tibeto-Burman Language Family George van Driem The Nagas speak languages of the Tibeto-Burman fami Ethnically, many Tibeto-Burman tribes of the northeast ly. Yet, according to our present state of knowledge, the have been called Naga in the past or have been labelled as >Naga languages< do not constitute a single genetic sub >Naga< in scholarly literature who are no longer usually group within Tibeto-Burman. What defines the Nagas best covered by the modern more restricted sense of the term is perhaps just the label Naga, which was once applied in today. Linguistically, even today's >Naga languages< do discriminately by Indo-Aryan colonists to all scantily clad not represent a single coherent branch of the family, but tribes speaking Tibeto-Burman languages in the northeast constitute several distinct branches of Tibeto-Burman. of the Subcontinent. At any rate, the name Naga, ultimately This essay aims (1) to give an idea of the linguistic position derived from Sanskrit nagna >naked<, originated as a titu of these languages within the family to which they belong, lar label, because the term denoted a sect of Shaivite sadhus (2) to provide a relatively comprehensive list of names and whose most salient trait to the eyes of the lay observer was localities as a directory for consultation by scholars and in that they went through life unclad. The Tibeto-Burman terested laymen who wish to make their way through the tribes labelled N aga in the northeast, though scantily clad, jungle of names and alternative appellations that confront were of course not Hindu at all. -

Trade Relationship Between Naga and Ahom Thesis
TRADE RELATIONSHIP BETWEEN NAGA AND AHOM THESIS SUBMITED IN PARTIAL FULFILMENT OF THE REQUIREMENT FOR THE DEGREE OF DOCTOR OF PHILOSOPHY TO NAGALAND UNIVERSTY Supervisor Research Scholar Prof. N.VENUH LICHUMO ENIE Department of History & Archaeology Nagaland University Kohima campus, Meriema. 2016 I dedicate this work to Almighty God My Father Shoshumo Enie and Mother Amhono Enie My wife Dr Hannah Enie and Son Mhajamo Enie My pillars of strength DECLARATION I, Shri. Lichumo Enie (PhD/433/2011) do hereby declare that the thesis entitled ‘Trade Relationship Between Naga and Ahom’ submitted by me under the guidance and research supervision of Professor N.Venuh, Department of History & Archaeology, Nagaland University is original and independent research work. I also declare that, it has not been submitted in any part or in full to this University or institution for the Award of any degree part or in full to this University or institution for the award of any degree. The thesis is being submitted to Nagaland University for the degree of Doctor of Philosophy in History and Archaeology. Prof. N.Venuh Prof. Y. Ben Lotha Lichumo Enie Supervisor Head Candidate CERTIFICATE This is to certify that the thesis ‘Trade Relationship Between Naga and Ahom’ bearing Regd. No. 433/2011 has been prepared by Lichumo Enie under my supervision. I certify that Lichumo Enie has fulfilled all norms required under the PhD regulations of Nagaland University for the submission of thesis for the Degree of Doctor of Philosophy of History & Archaeology. The thesis is original work based on his own research and analysis of materials. -

Download File
International Journal of Current Advanced Research ISSN: O: 2319-6475, ISSN: P: 2319-6505, Impact Factor: SJIF: 5.995 Available Online at www.journalijcar.org Volume 6; Issue 11; November 2017; Page No. 7239-7246 DOI: http://dx.doi.org/10.24327/ijcar.2017.7246.1108 Research Article NORTHEAST INDIA’S ARMED NAGA MOVEMENT: FROM CEASE FIRE TO FRAMEWORK AGREEMENT Aheibam Koireng Singh1., Sukhdeba Sharma Hanjabam2 and Homen Thangjam3 1Centre for Manipur Studies (CMS), Manipur University 2Dept. of Political Science, Indira Gandhi National Tribal University-Regional Campus Manipur 3Dept. of Social Work, Indira Gandhi National Tribal University-Regional Campus Manipur ARTICLE INFO ABSTRACT Article History: The armed political movement of the Nagas, has traversed a long way. One remarkable Received 20th August, 2017 achievement was that it could forge a political unity of identity among various tribes Received in revised form 29th speaking a thousand tongues inhabiting different realms of territorial spaces in different September, 2017 states of India and different regions in Myanmar, practicing different ways of lives. If the Accepted 30th October, 2017 solution comes in a package of secrecy as it is happening at the moment, compounding not Published online 28th November, 2017 only confusion but also the fear psychosis of the people of Manipur, the solution is bound to create more problem than peace. For instance, some sections of Nagas in Manipur are Key words: celebrating while the Nagas of Nagaland are sceptic that the agreement should not come Ceasefire, Constitution, Framework, Identity, out as a compromise. Similarly, the political class and the general public are worried that it Integrity, Kuki, Myanmar, Manipur, Naga, should not disturb Manipur’s Integrity. -

A Review on Electronic Dictionary and Machine Translation System Developed in North-East India
ORIENTAL JOURNAL OF ISSN: 0974-6471 COMPUTER SCIENCE & TECHNOLOGY June 2017, An International Open Free Access, Peer Reviewed Research Journal Vol. 10, No. (2): Published By: Oriental Scientific Publishing Co., India. Pgs. 429-437 www.computerscijournal.org A Review on Electronic Dictionary and Machine Translation System Developed in North-East India SAIFUL ISLAM* and BIPUL SYAM PURKAYASTHA Department of Computer Science, Assam University, Silchar, PIN-788011, Assam, India Corresponding author e-mail: [email protected] http://dx.doi.org/10.13005/ojcst/10.02.25 (Received: May 04, 2017; Accepted: May 12, 2017) ABSTRACT Electronic Dictionary and Machine Translation system are both the most important language learning tools to achieve the knowledge about the known and unknown natural languages. The natural languages are the most important aspect in human life for communication. Therefore, these two tools are very important and frequently used in human daily life. The Electronic Dictionary (E-dictionary) and Machine Translation (MT) systems are specially very helpful for students, research scholars, teachers, travellers and businessman. The E-dictionary and MT are very important applications and research tasks in Natural Language Processing (NLP). The demand of research task in E-dictionary and MT system are growing in the world as well as in India. North-East (NE) is a very popular and multilingual region of India. Even then, a small number of E-dictionary and MT system have been developed for NE languages. Through this paper, we want to elaborate about the importance, approaches and features of E-dictionary and MT system. This paper also tries to review about the existing E-dictionary and MT system which are developed for NE languages in NE India. -

History of the Scientific Study of the Tibeto-Burman Languages of North-East India
Indian Journal of History of Science, 52.4 (2017) 420-444 DOI: 10.16943/ijhs/2017/v52i4/49265 History of the Scientific Study of the Tibeto-Burman Languages of North-East India Satarupa Dattamajumdar* (Received 25 April 2017; revised 19 October 2017) Abstract Linguistics or in other words the scientific study of languages in India is a traditional exercise which is about three thousand years old and occupied a central position of the scientific tradition from the very beginning. The tradition of the scientific study of the languages of the Indo-Aryan language family which are mainly spoken in India’s North and North-Western part was brought to light with the emergence of the genealogical study of languages by Sir William Jones in the 18th c. But the linguistic study of the Tibeto-Burman languages spoken in North-Eastern part of India is of a much later origin. According to the 2011 census there are 45486784 people inhabiting in the states of North-East India. They are essentially the speakers of the Tibeto-Burman group of languages along with the Austro-Asiatic and Indo-Aryan groups of languages. Though 1% of the total population of India is the speaker of the Tibeto-Burman group of languages (2001 census) the study of the language and society of this group of people has become essential from the point of view of the socio-political development of the country. But a composite historical account of the scientific enquiries of the Tibeto-Burman group of languages, a prerequisite criterion for the development of the region is yet to be attempted. -
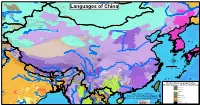
Map by Steve Huffman Data from World Language Mapping System 16
Mandarin Chinese Evenki Oroqen Tuva China Buriat Russian Southern Altai Oroqen Mongolia Buriat Oroqen Russian Evenki Russian Evenki Mongolia Buriat Kalmyk-Oirat Oroqen Kazakh China Buriat Kazakh Evenki Daur Oroqen Tuva Nanai Khakas Evenki Tuva Tuva Nanai Languages of China Mongolia Buriat Tuva Manchu Tuva Daur Nanai Russian Kazakh Kalmyk-Oirat Russian Kalmyk-Oirat Halh Mongolian Manchu Salar Korean Ta tar Kazakh Kalmyk-Oirat Northern UzbekTuva Russian Ta tar Uyghur SalarNorthern Uzbek Ta tar Northern Uzbek Northern Uzbek RussianTa tar Korean Manchu Xibe Northern Uzbek Uyghur Xibe Uyghur Uyghur Peripheral Mongolian Manchu Dungan Dungan Dungan Dungan Peripheral Mongolian Dungan Kalmyk-Oirat Manchu Russian Manchu Manchu Kyrgyz Manchu Manchu Manchu Northern Uzbek Manchu Manchu Manchu Manchu Manchu Korean Kyrgyz Northern Uzbek West Yugur Peripheral Mongolian Ainu Sarikoli West Yugur Manchu Ainu Jinyu Chinese East Yugur Ainu Kyrgyz Ta jik i Sarikoli East Yugur Sarikoli Sarikoli Northern Uzbek Wakhi Wakhi Kalmyk-Oirat Wakhi Kyrgyz Kalmyk-Oirat Wakhi Kyrgyz Ainu Tu Wakhi Wakhi Khowar Tu Wakhi Uyghur Korean Khowar Domaaki Khowar Tu Bonan Bonan Salar Dongxiang Shina Chilisso Kohistani Shina Balti Ladakhi Japanese Northern Pashto Shina Purik Shina Brokskat Amdo Tibetan Northern Hindko Kashmiri Purik Choni Ladakhi Changthang Gujari Kashmiri Pahari-Potwari Gujari Japanese Bhadrawahi Zangskari Kashmiri Baima Ladakhi Pangwali Mandarin Chinese Churahi Dogri Pattani Gahri Japanese Chambeali Tinani Bhattiyali Gaddi Kanashi Tinani Ladakhi Northern Qiang -

Abstract of Speakers' Strength of Languages and Mother Tongues - 2011
STATEMENT-1 ABSTRACT OF SPEAKERS' STRENGTH OF LANGUAGES AND MOTHER TONGUES - 2011 Presented below is an alphabetical abstract of languages and the mother tongues with speakers' strength of 10,000 and above at the all India level, grouped under each language. There are a total of 121 languages and 270 mother tongues. The 22 languages specified in the Eighth Schedule to the Constitution of India are given in Part A and languages other than those specified in the Eighth Schedule (numbering 99) are given in Part B. PART-A LANGUAGES SPECIFIED IN THE EIGHTH SCHEDULE (SCHEDULED LANGUAGES) Name of Language & mother tongue(s) Number of persons who Name of Language & mother tongue(s) Number of persons who grouped under each language returned the language (and grouped under each language returned the language (and the mother tongues the mother tongues grouped grouped under each) as under each) as their mother their mother tongue) tongue) 1 2 1 2 1 ASSAMESE 1,53,11,351 Gawari 19,062 Assamese 1,48,16,414 Gojri/Gujjari/Gujar 12,27,901 Others 4,94,937 Handuri 47,803 Hara/Harauti 29,44,356 2 BENGALI 9,72,37,669 Haryanvi 98,06,519 Bengali 9,61,77,835 Hindi 32,22,30,097 Chakma 2,28,281 Jaunpuri/Jaunsari 1,36,779 Haijong/Hajong 71,792 Kangri 11,17,342 Rajbangsi 4,75,861 Khari Boli 50,195 Others 2,83,900 Khortha/Khotta 80,38,735 Kulvi 1,96,295 3 BODO 14,82,929 Kumauni 20,81,057 Bodo 14,54,547 Kurmali Thar 3,11,175 Kachari 15,984 Lamani/Lambadi/Labani 32,76,548 Mech/Mechhia 11,546 Laria 89,876 Others 852 Lodhi 1,39,180 Magadhi/Magahi 1,27,06,825 4 DOGRI 25,96,767 -

Traditional Religion of the Lotha Nagas and the Impact of Christianity
TRADITIONAL RELIGION OF THE LOTHA NAGAS AND THE IMPACT OF CHRISTIANITY. A Thesis Submitted in fulfilment of the requirements for the Degree of DOCTOR OF PHILOSOPHY BY MHABENI EZUNG Department of History & Archaeology School of Social Sciences TO Nagaland University Kohima Campus: Meriema Headquarter: Lumami November 2014 Department of History and Archaeology Certificate Certified that the subject matter of this thesis is the record of work down by Ms. Mhabeni Ezung and the contents of this thesis did not form a basis of the award of any previous degree to her, or, to the best of my knowledge, to anyone else, and that the thesis had not been submitted by her for any research degree in any other university. In habit and character, Ms. Mhabeni Ezung is a fit and proper person for the degree of Doctor of Philosophy. Kohima The…..Nov. 2014 Dr. Y. BEN LOTHA Supervisor Department of History & Archaeology NU Kohima Campus Meriema Declaration I, Mhabeni Ezung, do hereby declare that the thesis entitled “Traditional Religion of the Lotha Nagas and the Impact of Christianity” submitted for the award of the degree of Doctor of Philosophy in History is my original work and that it has not previously formed the basis for the award of any degree on the same title Kohima: (Mhabeni Ezung) Date: Research Scholar Department of History & Archaeology Nagaland University Kohima. Countersigned Dr. Ketholesie Zetsuvi Dr.Y.Ben Lotha Head Supervisor Department of History & Archaeology Associate Professor Nagaland University Department of History & Archaeology Kohima Nagaland University Kohima ACKNOWLEDGEMENTS The completion of this thesis would not have been possible without the help of many, whose timely contributions, guidance and support I would like to acknowledge. -

Historical Account of British Legacy in the Naga Hills (1881- 1947)
Historical Account of British Legacy in the Naga Hills (1881- 1947) A thesis submitted to the Tilak Maharashtra Vidyapeeth, Pune For the degree of Vidyawachaspati (Ph.D) Department of History Under Faculty of Social Sciences Researcher Joseph Longkumer Research Supervisor: Dr. Shraddha Kumbhojkar March, 2011 1 Certificate I certify that the work presented here by Mr. Joseph Longkumer represents his original work that was carried out by him at Tilak Maharashtra Vidyapeeth, Pune under my guidance during the period 2007 to 2011. Work done by other scholars has been duly cited and acknowledged by him. I further certify that he has not submitted the same work to this or any other University for any research degree. Place: Signature of Research Supervisor 2 Declaration I hereby declare that this submission is my own work and that, to the best of my knowledge and belief, it contains no material previously published or written by another person nor material which has been accepted for the award of any degree or diploma of the University or other institute of higher learning, except where due acknowledgment has been made in the text. Signature Name Date 3 CONTENTS Page No. Acknowledgement CHAPTER – 1 Introduction……………………………………………………………………………………5 CHAPTER – II British Policy towards the Naga Hills with an Account of Tour in the Naga Hills………….54 CHAPTER – III State Of Affairs from 1910-1933…………………………………………………………...142 CHAPTER – IV Advent of Christianity and Modern Education……………………………………………..206 CHAPTER – V Nagas and the World War II………………………………………………………………...249 CHAPTER – VI Conclusion…………………………………………………………………………………..300 Bibliography….....................................................................................................................308 Appendices..........................................................................................................................327 4 Chapter 1 INTRODUCTION There is a saying among the Nagas that, at one point of time the Nagas wrote and maintained their history, written in some animal skin.