Volume 31, Issue 2
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Economic Gains of Realized Volatility in the Brazilian Stock Market
TEXTO PARA DISCUSSÃO No. 624 Economic gains of realized volatility in the Brazilian stock market Francisco Santos Márcio Garcia Marcelo Medeiros DEPARTAMENTO DE ECONOMIA www.econ.puc-rio.br Economic gains of realized volatility in the Brazilian stock market Abstract This paper evaluates the economic gains associated with following a volatility timing strategy based on a multivariate model of realized volatility. To study this issue we build a high frequency database with the most actively traded Brazilian stocks. Comparing with traditional volatility methods, we find that economic gains associated with realized measures perform well when estimation risk is controlled and increase proportionally to the target return. When expected returns are bootstrapped, however, performance fees are not significant, which is an indication that economic gains of realized volatility are offset by estimation risk. Keywords: Realized volatility, utility, forecasting. JEL Code: G11, G17. 1. Introduction Given the growth of financial markets and the increasing complexity of its securities, volatility models play an essential role to help the task of risk management and investment decisions. Since realization of volatility returns based on daily data is not observable, the traditional approach is to invoke parametric assumptions regarding the evolution of the first and second moments of the returns, which is the idea behind ARCH and stochastic volatility models. Nevertheless, these models fail to capture some stylized facts such as autocorrelation persistence and fat tail of returns. The availability of intraday data opens up the possibility of approximating volatility directly from asset returns. The use of an observable variable, in turn, facilitates the task of dealing with problems that involves a significant number of assets. -

United States Securities and Exchange Commission Form
UNITED STATES SECURITIES AND EXCHANGE COMMISSION Washington, D.C. 20549 FORM 20-F (Mark One) ☐ REGISTRATION STATEMENT PURSUANT TO SECTION 12(b) OR (g) OF THE SECURITIES EXCHANGE ACT OF 1934 OR ☒ ANNUAL REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the fiscal year ended December 31, 2015 OR ☐ TRANSITION REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 For the transition period from to . OR ☐ SHELL COMPANY REPORT PURSUANT TO SECTION 13 OR 15(d) OF THE SECURITIES EXCHANGE ACT OF 1934 Date of event requiring this shell company report Commission file number: 001-33356 GAFISA S.A. (Exact name of Registrant as specified in its charter) GAFISA S.A. (Translation of Registrant’s name into English) The Federative Republic of Brazil (Jurisdiction of incorporation or organization) Av. Nações Unidas No. 8,501, 19th Floor 05425-070 – São Paulo, SP – Brazil| phone: + 55 (11) 3025-9000 fax: + 55 (11) 3025-9348 e mail: [email protected] Attn: Andre Bergstein – Chief Financial Officer and Investor Relations Officer (Address of principal executive offices) Securities registered or to be registered pursuant to Section 12(b) of the Act: Title of each class Name of each exchange on which registered Common Shares, without par value* New York Stock Exchange * Traded only in the form of American Depositary Shares (as evidenced by American Depositary Receipts), each representing two common shares which are registered under the Securities Act of 1933. Securities registered or to be registered pursuant to Section 12(g) of the Act: None Securities for which there is a reporting obligation pursuant to Section 15(d) of the Act: None Indicate the number of outstanding shares of each of the issuer’s classes of capital or common stock as of the close of the period covered by the annual report. -

Novo Mercado and Its Followers: Case Studies in Corporate Governance Reform
5 Focus Novo Mercado and Its Followers: Case Studies in Corporate Governance Reform Maria Helena Santana Melsa Ararat Petra Alexandru B. Burcin Yurtoglu Mauro Rodrigues da Cunha Copyright 2008. For permission to photocopy or reprint, International Finance Corporation please send a request with complete 2121 Pennsylvania Avenue, NW information to: Washington, DC 20433 The International Finance Corporation All rights reserved. c/o the World Bank Permissions Desk Offi ce of the Publisher The fi ndings, interpretations, and 1818 H Street NW conclusions expressed in this publication Washington, DC 20433 should not be attributed in any manner to the International Finance Corporation, to All queries on rights and licenses its affi liated organizations, or to members including subsidiary rights should be of its board of Executive Directors addressed to: or the countries they represent. The International Finance Corporation does The International Finance Corporation not guarantee the data included in this c/o the Offi ce of the Publisher publication and accepts no responsibility World Bank for any consequence of their use. 1818 H Street, NW Washington, DC 20433 The material in this work is protected by Fax: +1 202-522-2422 copyright. Copying and/or transmitting portions or all of this work may be a violation of applicable law. The International Finance Corporation encourages dissemination of its work and hereby grants permission to the user of this work to copy portions for their personal, noncommercial use, without any right to resell, redistribute, or create derivative works there from. Any other copying or use of this work requires the express written permission of the International Finance Corporation. -

Template Word 2020
Itaúsa Head Office | Av. Paulista - SP Management’s Proposal and Ordinary and Extraordinary General Stockholders’ Meeting Manual April 30, 2021, 11:00 am Virtual-only format 1 Contents 1. Message from the Chairman of the Board and the CEO ............................................................................................. 3 2. Information about the Ordinary and Extraordinary General Stockholders’ Meeting ............................................. 4 a) Date, time and format .................................................................................................................................................................................... 4 b) Opening and approval quorums................................................................................................................................................................ 4 c) Documents made available to stockholders ......................................................................................................................................... 4 d) Attendance at the General Stockholders’ Meeting ............................................................................................................................ 4 Stockholders’ identification and representation documents (“Documents”).......................................................................... 5 Guidance on representation by proxies ................................................................................................................................................. -

Geographic Listing by Country of Incorporation
FOREIGN COMPANIES REGISTERED AND REPORTING WITH THE U.S. SECURITIES AND EXCHANGE COMMISSION December 31, 2010 Geographic Listing by Country of Incorporation COMPANY COUNTRY MARKET Antigua Sinovac Biotech Ltd. Antigua Global Mkt Argentina Alto Palermo S.A. Argentina Global Mkt Banco Macro S.A. Argentina NYSE BBVA Banco Frances S.A. Argentina NYSE Cresud Sacif Argentina Global Mkt Empresa Distribuidora y Comercializadora Norte S.A. - Edenor Argentina NYSE Grupo Financiero Galicia S.A. Argentina Global Mkt IRSA Inversiones y Representacions, S.A. Argentina NYSE MetroGas S.A. Argentina OTC Nortel Inversora S.A. Argentina NYSE Pampa Energia SA Argentina NYSE Petrobras Argentina S.A. Argentina NYSE Telecom Argentina S.A. Argentina NYSE Transportadora de Gas del Sur S.A. Argentina NYSE YPF S.A. Argentina NYSE Australia Allied Gold Ltd. Australia OTC Alumina Ltd. Australia NYSE BHP Billiton Ltd. Australia NYSE Genetic Technologies Ltd. Australia Global Mkt Metal Storm Ltd. Australia OTC Novogen Ltd. Australia Global Mkt Orbital Corp Ltd. Australia OTC Prana Biotechnology Ltd. Australia Cap. Mkt Progen Pharmaceuticals Ltd. Australia OTC Rio Tinto Ltd. Australia OTC Samson Oil & Gas Ltd. Australia NYSE-Amex Sims Metal Management Ltd. Australia NYSE Westpac Banking Corp. Australia NYSE Bahamas Calpetro Tankers (Bahamas I) Ltd. Bahamas OTC - Debt Calpetro Tankers (Bahamas II) Ltd. Bahamas OTC - Debt Calpetro Tankers (Bahamas III) Ltd. Bahamas OTC - Debt Ultrapetrol (Bahamas) Ltd. Bahamas Global Mkt Belgium Anheuser-Busch Inbev SA/NV Belgium NYSE Etablissements Delhaize Freres & Cie - Le Lion Belgium NYSE Page 1 COMPANY COUNTRY MARKET Bermuda AllShips Ltd. Bermuda OTC Alpha and Omega Semiconductor Ltd. Bermuda Global Mkt Asia Pacific Wire & Cable Corp. -
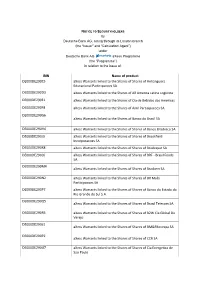
DE000DE290C5 Axess Warrants Linked to the Shares of Shares Of
NOTICE TO SECURITYHOLDERS by Deutsche Bank AG, acting through its London branch (the “Issuer” and “Calculation Agent”) under Deutsche Bank AG aXess Programme (the “Programme”) in relation to the issue of: ISIN Name of product DE000DE290C5 aXess Warrants linked to the Shares of Shares of Anhanguera Educacional Participacoes SA DE000DE290D3 aXess Warrants linked to the Shares of All America Latina Logistica DE000DE290E1 aXess Warrants linked to the Shares of Cia de Bebidas das Americas DE000DE290F8 aXess Warrants linked to the Shares of Amil Participacoes SA DE000DE290G6 aXess Warrants linked to the Shares of Banco do Brasil SA DE000DE290H4 aXess Warrants linked to the Shares of Shares of Banco Bradesco SA DE000DE290J0 aXess Warrants linked to the Shares of Shares of Brookfield Incorporacoes SA DE000DE290K8 aXess Warrants linked to the Shares of Shares of Bradespar SA DE000DE290L6 aXess Warrants linked to the Shares of Shares of BRF ‐ Brasil Foods SA DE000DE290M4 aXess Warrants linked to the Shares of Shares of Braskem SA DE000DE290N2 aXess Warrants linked to the Shares of Shares of BR Malls Participacoes SA DE000DE290P7 aXess Warrants linked to the Shares of Shares of Banco do Estado do Rio Grande do Sul S.A. DE000DE290Q5 aXess Warrants linked to the Shares of Shares of Brasil Telecom SA DE000DE290R3 aXess Warrants linked to the Shares of Shares of B2W Cia Global Do Varejo DE000DE290S1 aXess Warrants linked to the Shares of Shares of BM&FBovespa SA DE000DE290T9 aXess Warrants linked to the Shares of Shares of CCR SA DE000DE290U7 aXess -

Universidade Federal Do Rio De Janeiro Análise Operacional-Financeira Das Maiores Empresas Por Valor De Mercado Do Setor Imobil
UNIVERSIDADE FEDERAL DO RIO DE JANEIRO ANÁLISE OPERACIONAL-FINANCEIRA DAS MAIORES EMPRESAS POR VALOR DE MERCADO DO SETOR IMOBILIÁRIO BRASILEIRO AO LONGO DA DÉCADA 2008-2018 NICOLAS SMECELATO MARCONDES CESAR 2019 ANÁLISE OPERACIONAL-FINANCEIRA DAS MAIORES EMPRESAS POR VALOR DE MERCADO DO SETOR IMOBILIÁRIO BRASILEIRO AO LONGO DA DÉCADA 2008-2018 NICOLAS SMECELATO MARCONDES CESAR Projeto de Graduação apresentado ao curso de Engenharia Civil da Escola Politécnica, Universidade Federal do Rio de Janeiro, como parte dos requisitos necessários à obtenção do título de Engenheiro. Orientador: Prof. Thereza Cristina Nogueira de Aquino, DSc RIO DE JANEIRO 2019 Resumo do Projeto de Graduação apresentado à Escola Politécnica/ UFRJ como parte dos requisitos necessários para a obtenção do grau de Engenheiro Civil. ANÁLISE OPERACIONAL-FINANCEIRA DAS MAIORES EMPRESAS POR VALOR DE MERCADO DO SETOR IMOBILIÁRIO BRASILEIRO AO LONGO DA DÉCADA 2008-2018 Nicolas Smecelato Marcondes Cesar Dezembro de 2019 Orientador: Thereza Cristina Nogueira de Aquino, DSc Após anos de amplo crescimento e fortes resultados entre 2008 e 2013, o setor imobiliário brasileiro se tornou um dos setores mais impactados pela subsequente recessão econômica. Atuando em diferentes nichos de mercado, as grandes construtoras utilizaram diferentes estratégias operacionais e financeiras para aprimorarem suas margens e se manterem competitivas. O presente trabalho visa expor e analisar o impacto das diferentes soluções estratégicas nos resultados operacionais e financeiros das grandes construtoras brasileiras, bem como na dinâmica competitiva de tais empresas ao longo da década 2008- 2018. Serão analisados, através de técnicas de contabilidade e gestão, os balanços operacionais-financeiros das grandes construtoras, bem como indicadores macroeconômicos e setoriais. -

412 NYSE and Arca-Listed Non-U.S. Issuers from 45 Countries (As of December 31, 2008) Share Country Issuer † Symbol Industry Listed Type IPO
412 NYSE and Arca-listed non-U.S. Issuers from 45 Countries (as of December 31, 2008) Share Country Issuer † Symbol Industry Listed Type IPO ARGENTINA (11 DR Issuers ) Banco Macro S.A. BMA Banking 3/24/06 A IPO BBVA Banco Francés S.A. BFR Banking 11/24/93 A IPO Empresa Distribuidora y Comercializadora Norte S.A. (Edenor) EDN Electricity Distribution 4/26/07 A IPO IRSA-Inversiones y Representaciones, S.A. IRS Real Estate Development 12/20/94 G IPO MetroGas, S.A. MGS Gas Distribution 11/17/94 A IPO Nortel Inversora S.A. NTL Telecommunications 6/17/97 A IPO Petrobras Energía Participaciones S.A. PZE Holding Co./Oil/Gas Refining 1/26/00 A Telecom Argentina S.A. TEO Telecommunications 12/9/94 A Telefónica de Argentina, S.A. TAR Telecommunications 3/8/94 A Transportadora de Gas del Sur, S.A. TGS Gas Transportation 11/17/94 A YPF Sociedad Anónima YPF Oil/Gas Exploration 6/29/93 A IPO AUSTRALIA (5 ADR Issuers ) Alumina Limited AWC Diversified Minerals 1/2/90 A BHP Billiton Limited BHP Mining/Exploration/Production 5/28/87 A IPO James Hardie Industries N.V. JHX International Bldg. Materials 10/22/01 A Sims Group Limited SMS Metals Recycling 3/17/08 A Westpac Banking Corporation WBK Banking 3/17/89 A IPO BAHAMAS (4 non-ADR Issuers ) Teekay LNG Partners L.P. TGP Liquified Natural Gas Transp. 5/505 O IPO Teekay Offshore Partners L.P. TOO Marine Transportation & Storage Svcs. 12/14/06 O IPO Teekay Corporation TK Crude Oil/Petroleum Transportation 7/20/95 O IPO Teekay Tankers Ltd. -

Price Target Sensitivity Discounted Cash
Alpha Challenge Long EVEN Construtora e Incorporadora S.A. (EVEN3.BZ) Short KB Homes (NYSE: KBH) Steve Schembri, Bradley Murray, Gustav Karlsson 18th November, 2011 Recommendation Long EVEN Construtora Short KB Homes • Current Price: R$ 6.38 • Current Price: $7.51 • Target Price: R$ 12.29 • Target Price: $4.97 • Target Return: +93% • Target Return: +34% • Position Size: R$ 50 million • Position Size: $25 million • Thesis (Fundamentals) • Thesis (Event Driven) 1. Secular tailwinds 1. Serious liquidity concerns 2. Mid-income segment focus 2. Inventory in hardest hit areas 3. Best-in-class capital allocation 3. Exposure to first-time buyers 4. Incentivized leadership 4. Structural problems in market 5. Supportive valuation 5. Low inventory vis-à-vis peers • Catalysts • Catalysts 1. Q4 inflation inflection point 1. Potential S&P downgrade 2. Prudent monetary policy 2. Dividend cut 3. Analyst upward revision 3. Failed bond auction in 2012 4. Q411E CF underperformance Agenda Long EVEN Construtora • Macro Outlook: Brazil • Buy Recommendation Short KB Homes • Macro Outlook: US • Sell Recommendation Macro Outlook BRAZIL Favorable Macroeconomic Tailwinds Population, Unemployment, Real GDP • Young and growing population Millions growth • 100mm people (50% of country) 210 15% between 20 and 59 years old 200 10% • Average GDP growth of 3.6% 190 5% over the past 10 years 180 0% • Unemployment rate at 6% 170 -5% 1 • Low leverage among consumer 2004 05 06 07 08 09 10 11F 12F 13F base Population (LHS) Unemployment (RHS) Real GDP (RHS) Mortgage Debt / GDP (2009) 100% 80% • Increased consumer purchasing 60% power 40% • Ability to “lever up” 20% 0% UK USA Chile Spain Brazil China Korea France Turkey Poland Mexico Canada Portugal Thailand Australia Germany Argentina Hong KongHong New ZealandNew Source: Bloomberg; Broker research: DB (19 Aug 2010) 1. -

23 De Março De 2017 Prezado Acionista Da Gafisa SA
23 de março de 2017 Prezado Acionista da Gafisa S.A.: Temos a satisfação de informar que o reposicionamento anteriormente anunciado da Gafisa S.A., ou “Gafisa”, por meio da separação de sua subsidiária integral, Construtora Tenda S.A., uma sociedade anônima constituída segundo as leis da República Federativa do Brasil, ou “Tenda”, de nossos negócios remanescentes deverá se materializar até o final de maio de 2017. A Tenda se tornará uma sociedade anônima independente da Gafisa no que diz respeito às suas operações e estrutura de capital, e deterá através de suas subsidiárias, os ativos e passivos associados ao segmento econômico residencial da Gafisa no Brasil. A Tenda iniciou o processo para listar suas ações na BM&FBovespa S.A. – Bolsa de Valores Mercadorias e Futuros, ou “BM&FBOVESPA”, de modo que as ações da Tenda sejam aceitas para negociação até 31 de maio de 2017. Como parte da separação, 50% do capital social da Tenda, ou as “Ações Ofertadas”, serão vendidas e os 50% restantes do capital social da Tenda serão transferidos aos acionistas da Gafisa através da redução do capital social total da Gafisa. Com relação à venda, em 14 de dezembro de 2016, a Gafisa celebrou um contrato de compra e venda de ações, ou “SPA”, com a Jaguar Real Estate Partners, LP, ou “Jaguar”, segundo o qual a Gafisa venderá as ações da Tenda representando até 30% do capital social total da Tenda, ao preço equivalente a R$ 8,13 por ação, ou o “Preço por Ação”. Segundo o SPA, a Gafisa receberá proventos de R$ 231,7 milhões, avaliando o capital social da Tenda em R$ 539,0 milhões. -

Market Overview 47.600 Fechamento: O Ibovespa Encerrou a Sessão Em Alta De 0,44%, a 47.447 Pontos, Impulsionado Pela Valorização De Ações De Bancos
Citi Corretora Diário do Mercado 20 de o utubro de 2015 Ibovespa – Intra Day Market Overview 47.600 Fechamento: O Ibovespa encerrou a sessão em alta de 0,44%, a 47.447 pontos, impulsionado pela valorização de ações de bancos. Nos EUA, as bolsas 47.400 foram pressionadas por resultados trimestrais abaixo das expectativas. 47.200 Destaque do dia ficou para a queda nas commodities após dados mostrando 47.000 desaceleração da economia chinesa. O dólar e os DIs futuros apresentaram queda. O giro financeiro totalizou R$ 5,2 bilhões, 28% abaixo da média das 46.800 últimas 20 sessões. 46.600 10 11 12 14 15 17 Mercado hoje: Bolsas com desempenho misto. Na Ásia, mercados fecharam em leve alta (China +1,1%; Japão +0,4%), enquanto na Europa as bolsas Performance (%) negociam em queda, com setores de energia e mineração mais pesados. O Fech. Dia Sem. Mês Ano petróleo opera em queda de 1%, mesma direção do minério. Nos EUA, índices Ibovespa 47.447 0,4 (3,8) 5,3 (5,1) futuros em leve queda, à espera de dados de moradia que serão divulgados às 10h30. Fechando a agenda, a presidente do Fed – Janet Yellen – fará discurso IBX-50 8.111 0,4 (3,8) 4,8 (4,2) às 13h00. S&P 500 2.034 0,0 0,8 5,9 (1,2) Dow Jones 17.231 0,1 0,6 5,8 (3,3) Empresas & Setores Nasdaq 4.905 0,4 1,4 6,2 3,6 Dólar Ptax 3,901 1,5 4,4 (1,8) 46,9 . -

Climate Advisers' Deforestation Risk Rankings
Climate Advisers’ Deforestation Risk Rankings Rankings Methodology & Results Niamh McCarthy Peter Graham Ameer Azim Climate Advisers’ Deforestation RisK Rankings | 1 Ranking Description/Theme The Climate Advisers Deforestation RisK RanKing report is a regional ranKing of public companies with direct or indirect exposure to deforestation driven by tropical commodities. Companies in Latin America, North America, and Asia (excluding Japan) were ranked according to relative performance on enacting policy and process controls to mitigate the environmental, social, and governance (ESG) risks of planetary deforestation impacts. Particular consideration was given to company actions, policies, and certifications in palm oil, soy, timber, and beef supply chains. Rating Highlights The Climate Advisers Deforestation RisK RanKings is built using Thomson Reuters ESG and controversy data, along with published Forest 500, CDP, and SPOTT rankings and relevant company participation in Roundtable on Sustainable Palm Oil (RSPO), Roundtable on Responsible Soy Association (RTRS), and Global Roundtable for Sustainable Beef (GRSB) certifications. The ranKings universe is made up of companies incorporated in Latin America, Asia (ex. Japan), and North America respectively. Companies are rated by Thomson Reuters ESG Research and strictly screened against universal exclusionary and inclusionary criteria. The companies are evaluated against 93 of the 424 indicators available from Thomson Reuters ESG. The total includes 25 “social” indicators, 33 “environmental” indicators, and 25 “controversy” indicators. A share of the final score is the published Thomson Reuters/S-NetworK ESG Best Practices Governance Score. An additional 18 topical indicators are researched by Climate Advisers staff and computed in the final rating. Scoring Indicators are appropriately weighted to signal relevance to industry peer groups.