DOCSLIB.ORG

Formally Verified Invariants of Vote Counting Schemes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Formally Verified Invariants of Vote Counting Schemes Formally Verified Invariants of Vote Counting Schemes ∗ Florrie Verity Dirk Pattinson The Australian National University The Australian National University ABSTRACT system is universally verifiable if any member of the general The correctness of ballot counting in electronically held elec- public has means to determine whether all ballots cast have tions is a cornerstone for establishing trust in the final re- been counted correctly. End-to-end verifiability is usually sult. Vote counting protocols in particular can be formally achieved by complex cryptographic methods and generate specified by as systems of rules, where each rule application receipts that voters can use to verify integrity of their bal- represents the effect of a single action in the tallying process lot, without revealing the ballot content. None of the current that progresses the count. We show that this way of formal- voting systems in existence [16, 4, 11, 5] offers universal ver- ising vote counting protocols is also particularly suitable for ifiability of the tallying in elections that rely on complex, (formally) establishing properties of tallying schemes. The preferential voting schemes such as single transferable vote key notion is that of an invariant: properties that transfer used in the majority of elections in Australia. That is, there from premiss to conclusion of all vote counting rules. We is no way for voters or political parties to verify the correct- show that the rule-based formulation of tallying schemes al- ness of the count. lows us to give transparent formal proofs of properties of the This is mediated, for example by the Australian Elec- respective scheme with relative ease. As our proofs are based toral Commission, by publishing both the ballots cast, and on the specification of vote counting protocols, rather than a scrutiny sheets that detail the proceeds of the count, on the program that implements them, we are guaranteed that the web so that individuals (or political parties) can run their property holds for every possible specification-confirming own vote-counting software on the published data. Our ex- implementation of the respective protocol. This in particu- perience indicates that while this is likely to generate the lar includes the vote counting programs that are automati- same election result, it is nearly impossible to generate tal- cally extracted from the specification. We demonstrate this lies that perfectly match those published on the web. The point by means of two examples: the monotonicity criterion reason for this is one of under-specification: the data pub- for majority (first-past-the-post) voting, and the majority lished by the electoral commission is noisy in the sense that criterion for a simple version of single transferable vote. some ballots assign the same preference to more than one candidate, or omit certain preferences altogether and the commission does not specify how votes of this kind are to 1. INTRODUCTION be accounted for. More generally, the specification of the Our trust in traditional paper-based elections largely de- vote counting scheme is usually given in the form of a le- rives from the fact that all stages of the process are wit- gal document which is not always unambiguous, specifically nessed by scrutineers, variously members of the general pub- concerning rare corner cases. lic or delegates nominated by stakeholders that ensure, and The correctness of the implementation of vote counting testify to, proper procedures being followed. In an elec- schemes has therefore been subject to a number of approaches tronic voting context [14], this is replicated by the concept based on formal methods. One generally distinguishes be- of end-to-end verifiability and universal verifiability. End- tween heavy weight and light weight approaches, where the to-end verifiable systems allow the voters to verify that their former involve the use of interactive theorem provers to es- vote has been correctly recorded, not been tampered with tablish mathematical correctness, and the latter rely on au- in (elecctronic) transit to the counting station and has been tomated or semi-automated techniques. In the domain of correctly included in the electronic ballot box. A voting electronic voting, it has been recognised that light-weight approaches are not practical for the task at hand [6, 2] and ∗Coq sources that accompany this paper are available from users.cecs.anu.edu.au/~dpattinson/Software/. heavy-weight methods, i.e. the use of interactive theorem provers, are necessary to give the desired correctness guar- antees. In the context of formal verification, the styles of Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed specifying vote counting schemes vary considerably, and usu- for profit or commercial advantage and that copies bear this notice and the full cita- ally some variant of type theory or higher-order logic is used tion on the first page. Copyrights for components of this work owned by others than to express the desired properties, see e.g. [7]. In contrast to ACM must be honored. Abstracting with credit is permitted. To copy otherwise, or re- publish, to post on servers or to redistribute to lists, requires prior specific permission directly encoding vote counting schemes, it has been advo- and/or a fee. Request permissions from [email protected]. cated in [15] that the best way of making the vote counting scheme precise is to give a formal specification by means c 2016 ACM. ISBN 978-1-4503-2138-9. of rules. The rule-based specification of voting protocols DOI: 10.1145/1235 is centred around states of the counting process that may property once counting terminates. We emphasise that we be thought of as photographic snapshots of a (n imagined) do not prove these properties on the basis of having an im- room where counting takes place. More abstractly, a state plementation of a concrete counting scheme (as done e.g. in records all information that are relevant for the counting [9] for plurality voting) but instead are basing our proofs on process at a given point in time. A rule then specifies how a (formal) specification of the scheme. As a consequence, this state may be manipulated by an (imagined) official pro- every implementation that (provably) conforms to the spec- gressing the count. An example of such an action would be ification, including in particular those synthesised from the \take a ballot from the pile of uncounted votes, update the specification itself, can be guaranteed to enjoy this property. tally of the candidate named as first preference, and put In other words: the implementation of vote counting accord- the ballot paper onto the pile of first-preference votes for ing to the FPTP and STV schemes that we have synthesised this candidate". As such, the description of the state invari- from the specification in [15] are automatically guaranteed to ably contains the running tally, a list of uncounted ballot satisfy monotonicity (resp. majority) criterion. papers, and, for every candidate, a list of votes counted in Formal proofs that involve properties of formal specifi- their favour. The count then progresses, in analogy with cations like the two criteria discussed above also serve a the paper-based process, by applying rules that (correctly) function beyond establishing that the criteria in fact hold: manipulate the state of the count, until winners can be de- they provide a basic sanity check of the formal specification. clared. As a consequence, we can understand a (formal) Just as for programs, humans invariably introduce errors specification of a voting scheme as a set of rules that ma- into specifications, rendering the fact that a program imple- nipulate the state of the count. It has been argued in [15] ments a specification virtually useless. Giving formal proofs that this way of specifying voting schemes is both natural that the specification satisfies the expected properties thus and leads to a receipt (the sequence of counting rules lead- increases our trust in the correctness of the specification as ing to the election outcome) that is both precise and can be such. In an area such as electronic voting where we would checked by correctness, i.e. provides a universally verifiable demand that programs conform to formal specification, we receipt of the correctness of the count. see the process of validating specifications as particularly In this paper, we argue that the rule-based approach to important. the specification of voting protocols is also well-suited to es- On a conceptual level, we demonstrate that rule-based tablishing properties of voting protocols specified in this way, specifications can not only capture the specifics of voting and so provides an orthogonal check on the correctness of the protocols in a natural way, but are moreover well-suited to specification. We demonstrate this by re-visiting two pro- their analysis. By giving loose specifications of the protocols tocols, simple plurality voting or first-past-the-post (FPTP) under scrutiny we achieve coverage of more than one variant and a simple version of single transferable vote (STV), both (or implementation) of the scheme. This introduces a very described in detail in Sections 2.1 and 2.2, respectively. In convenient layer of abstraction, as any implementation of a plurality voting, every voter votes for precisely one candi- voting protocol would reasonably be expected to satisfy its date, and the candidate with the highest tally wins. It specification, and our proofs entail that any specification- is known in the literature that this procedure satisfies the conforming implementation will satisfy the criteria under monotonicity criterion: consideration. That is, there is no need to re-establish any criteria that have been established on the level of specifi- If a candidate wins an election, they will still cation, as all implementations (in particular including the win the election if any number of ballot papers one that has been synthesised from the specification) are have been changed in their favour.
Load more

Recommended publications
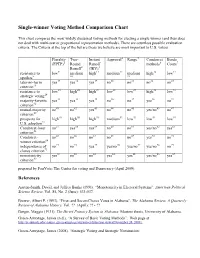
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
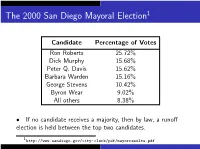
  • The Plurality-With-Elimination Method (PWE)
    The 2000 San Diego Mayoral Election1 Candidate Percentage of Votes Ron Roberts 25.72% Dick Murphy 15.68% Peter Q. Davis 15.62% Barbara Warden 15.16% George Stevens 10.42% Byron Wear 9.02% All others 8.38% • If no candidate receives a majority, then by law, a runoff election is held between the top two candidates. 1http://www.sandiego.gov/city-clerk/pdf/mayorresults.pdf Example: The 2000 San Diego Mayoral Election Practical problems with this system: I Runoff elections cost time and money I Ties (or near-ties) for second place I Preference ballots provide a method of holding an “instant-runoff" election: the Plurality-with-Elimination Method (PWE). 2. If no candidate has received a majority, then eliminate the candidate with the fewest first-place votes. 3. Repeat steps 1 and 2 until some candidate has a majority, then declare that candidate the winner. The Plurality-with-Elimination Method (x1.4) 1. Count the first-place votes. If some candidate receives a majority of the first-place votes, then that candidate is the winner. 3. Repeat steps 1 and 2 until some candidate has a majority, then declare that candidate the winner. The Plurality-with-Elimination Method (x1.4) 1. Count the first-place votes. If some candidate receives a majority of the first-place votes, then that candidate is the winner. 2. If no candidate has received a majority, then eliminate the candidate with the fewest first-place votes. The Plurality-with-Elimination Method (x1.4) 1. Count the first-place votes. If some candidate receives a majority of the first-place votes, then that candidate is the winner.
    [Show full text]
  • Arrow's Impossibility Theorem
    Arrow’s Impossibility Theorem Some announcements • Final reflections due on Monday. • You now have all of the methods and so you can begin analyzing the results of your election. Today’s Goals • We will discuss various fairness criteria and how the different voting methods violate these criteria. Last Time We have so far discussed the following voting methods. • Plurality Method (Majority Method) • Borda Count Method • Plurality-with-Elimination Method (IRV) • Pairwise Comparison Method • Method of Least Worst Defeat • Ranked Pairs Method • Approval Voting Fairness Criteria The following fairness criteria were developed by Kenneth Arrow, an economist in the 1940s. Economists are often interested in voting theories because of their impact on game theory. The mathematician John Nash (the subject of A Beautiful Mind) won the Nobel Prize in economics for his contributions to game theory. The Majority Criterion A majority candidate should always be the winner. Note that this does not say that a candidate must have a majority to win, only that such a candidate should not lose. Plurality, IRV, Pairwise Comparison, LWD, and Ranked Pairs all satisfy the Majority Criterion. The Majority Criterion The Borda Count Method violates the Majority Criterion. Number of voters 6 2 3 1st A B C 2nd B C D 3rd C D B 4th D A A Even though A had a majority of votes it only has 29 points. B is the winner with 32 points. Moral: Borda Count punishes polarizing candidates. The Condorcet Criterion A Condorcet candidate should always be the winner. Recall that a Condorcet Candidate is one that beats all other candidates in a head-to-head (pairwise) comparison.
    [Show full text]
  • Borda Count, Pairwise Comparison, Approval Voting, Fairness Criteria
    Day 2: Borda count, Pairwise Comparison, Approval Voting, Fairness Criteria Recall: Consider the voting system below. Who is the winner under the IRV method? 10 of the voters who had originally voted in the order Brown, Adams, Carter change their vote to favor the presumed winner changing those votes to Adams, Brown, Carter. Who is the winner under the IRV method? Monotonicity Criterion If voters change their votes to increase the preference for a candidate, it should not harm that candidate’s chances of winning. Boda count: (Another voting method, named for Jean-Charles de Borda) In this method, points are assigned to candidates based on their ranking; 1 point for last choice, 2 points for second-to-last choice, and so on. The point values for all ballots are totaled, and the candidate with the largest point total is the winner. Ex1) A camping club is deciding where to go on their next trip. The preference table is shown below, Find the winner under Borda count method. A = Arches, G = Grand Canyon, Y = Yosemite, Z = Zion Number of voters 12 5 4 9 6 10 1st Choice Y G Z A A Z 2nd Choice Z Y A Y Z G 3rd Choice G A G G Y A 4th Choice A Z Y Z G Y Since there are 4 choices 1th Place gets 4 points 2th Place gets 3 points 3th Place gets 2 points 4th Place gets 1point Number of voters 12 5 4 9 6 10 1st Choice Y G Z A A Z 4Point 12.4=48 5.4=20 4.4=16 9.4=36 6.4=24 10.4=40 2nd Choice Z Y A Y Z G 3Point 12.3=36 5.3=15 4.3=12 3rd Choice G A G G Y A 2Point 5.2=1o 10.2=20 4th Choice A Z Y Z G Y 1Point 12.1=12 Total points: Arches = 36 + 24 + 12 +10 +10 +20 +12 = 114 Grand Canyon = 106 Yosemite = 116 Zion = 124 Under the Borda count method Zion is the winner What’s Wrong with Borda Count? One potential flaw of Borda count is a candidate could receive a majority of the first- choice votes and still lose the election.
    [Show full text]
  • Which Voting System Is Best for Canada?
    Electoral Reform: Which Voting System is Best For Canada? By David Piepgrass While watching the election coverage last Monday night, I was disconcerted by claims from party leaders and even journalists, suggesting that Canadians had “asked” for various things by their voting: “Canadians have asked our party to take the lead” “Canadians have selected a new government.” “Although Canadians have voted for change, they have not given any one party a majority in the House of Commons. They have asked us to cooperate, to work together, and to get on with tackling the real issues that matter to ordinary working people and their families.” - Stephen Harper “Canadians have asked the Conservatives to form a government – in a minority Parliament” “while the people of Canada asked Mr. Harper to form a minority government, the people of Canada also asked New Democrats to balance that government...” - Jack Layton But I voted in the election, and guess what I didn't see on the ballot? I wonder what they based their statements on. Votes vs. Seats (Federal Election 2006) Probably, it was either the popular vote or the Conservatives makeup of the government, but isn't it odd that the Liberals two are different? You can see the dichotomy NDP Percent of vote between the popular vote and the seat allocation Bloc Percent of on the right. It looks like the NDP and Bloc have Other seats somehow confused each other's seats, but actually, 0 5 10 15 20 25 30 35 40 45 as Canadian elections go, this one isn't too bad.
    [Show full text]
  • Voting Criteria
    Voting Criteria 21-301 2018 30 April 1 Evaluating voting methods In the last session, we learned about different voting methods. In this session, we will focus on the criteria we use to evaluate whether voting methods are doing their jobs; that is, the criteria we use to determine if a voting system is reasonable and fair. We use all notation as in the previous set of notes. 1. Majority Criterion: If a candidate gets > 50% of the first place votes, that candidate should be the winner. This criterion is quite straightforward. If a candidate is preferred by more than half of the voters, this candidate by all rights should win the election. No other candidate could be more satisfactory for more people than the first choice of more than 50% of the voters. It is immediately obvious that the plurality method and the runoff methods will satisfy this criterion, since their method of determining the winner is fundamentally based on first place votes. For other methods, the criterion is less clear. 2. Condorcet Criterion: If a candidate wins every pairwise comparison, then that candidate should be the winner. This should remind you of the Condorcet method for choosing a winner. Of course, it is immediately obvious that if the Condorcet method produces a winner without having to resolve ties, then that candidate wins the election in that method, so clearly the Condorcet method satisfies the Condorcet criterion. However, it is not clear that the other methods will satisfy this criterion; for example, in Hare method, is it possible to eliminate a candidate that would otherwise be a Condorcet winner? 3.
    [Show full text]
  • Chapter 9 Social Choice: the Impossible Dream
    Chapter 9 Social Choice: The Impossible Dream For All Practical Purposes: Effective Teaching • Talk to your fellow TA’s during the term and find out how their sessions are set up and how they are going. Talking about student problems and how they were handled can help both you and your colleagues in becoming confident educators. • In this chapter and others involving voting, you will represent candidates by letters such as A, B, C, or D. A good habit to get into early on, in general, is to use capital letters in cases such as this or if multiple-choice responses are requested. You can also impart to students that if lower case letters are used (like “a” or “d”) and their answers are not clear, then it is possible that their response will be marked as incorrect. Chapter Briefing Social choice theory was developed to analyze the various types of voting methods, to discover the potential pitfalls in each, and to attempt to find improved systems of voting. One difficulty you may encounter imparting to students is the need for various voting methods and their mathematical nature. Discussions can start with examining two candidate races and the simplicity of invoking majority rule. When there are three or more candidates, however, different and more complicated voting techniques may be required. Students may have difficulties grasping the differences between the voting methods and in turn the different criterion. Being well prepared by knowing these methods and criterion is essential for successful classroom discussions. In your academic preparation, you may not have encountered the topic of Social Choice.
    [Show full text]
  • Fairness Criteria Voting Methods
    VOTING METHODS FAIRNESS CRITERIA Majority Criterion – If a candidate wins by a Majority – receiving more than half of the first majority, then that candidate should win the place votes election by another method. Evaluation – If the majority winner does not win by another Plurality Method – receiving the most first place method, then this criterion is violated. If votes majority winner does win by another method, then it is not violated. Plurality with Elimination – Check first place votes for a majority. If candidate has a majority, then Head-to-head Criterion – If a candidate wins by declared winner. If not, eliminate the candidate head-to-head (pairwise) over every other with the fewest first place votes and recount. candidate, then that candidate should win the Recount. Continue until a candidate wins by a election. Evaluation – If one candidate wins over majority. all others when paired up and does not win by another method, then the criterion is violated. If Borda Count Method – Voters rank candidates on by another method, the head-to-head winner ballot. Assign 1 point to last place, 2 points to next, still wins, then the criterion is not violated. etc. Total points for each candidate. Candidate with the most points wins. Irrelevant Alternatives Criterion – A candidate wins. In a recount the only changes are that one Pairwise Comparison (Head-to-Head) Method – or more of the candidates are removed. Original Voters rank candidates on ballot. Pair up winner should win. Evaluation – A candidate candidates so each is compared with every other. drops out. Look at the 1st place votes.
    [Show full text]
  • Voting Theory 35
    Voting Theory 35 Voting Theory In many decision making situations, it is necessary to gather the group consensus. This happens when a group of friends decides which movie to watch, when a company decides which product design to manufacture, and when a democratic country elects its leaders. While the basic idea of voting is fairly universal, the method by which those votes are used to determine a winner can vary. Amongst a group of friends, you may decide upon a movie by voting for all the movies you’re willing to watch, with the winner being the one with the greatest approval. A company might eliminate unpopular designs then revote on the remaining. A country might look for the candidate with the most votes. In deciding upon a winner, there is always one main goal: to reflect the preferences of the people in the most fair way possible. Preference Schedules To begin, we’re going to want more information than a traditional ballot normally provides. A traditional ballot usually asks you to pick your favorite from a list of choices. This ballot fails to provide any information on how a voter would rank the alternatives if their first choice was unsuccessful. Preference ballot A preference ballot is a ballot in which the voter ranks the choices in order of preference. Example 1 A vacation club is trying to decide which destination to visit this year: Hawaii (H), Orlando (O), or Anaheim (A). Their votes are shown below: Bob Ann Marv Alice Eve Omar Lupe Dave Tish Jim 1st choice A A O H A O H O H A 2nd choice O H H A H H A H A H 3rd choice H O A O O A O A O O These individual ballots are typically combined into one preference schedule, which shows the number of voters in the top row that voted for each option: 1 3 3 3 1st choice A A O H 2nd choice O H H A rd 3 choice H O A O Notice that by totaling the vote counts across the top of the preference schedule we can recover the total number of votes cast: 1+3+3+3 = 10 total votes.
    [Show full text]
  • A Comprehensive Review of Voting Systems and a Proposal For
    A Comprehensive Review of Voting Systems and a Proposal for Connecticut February 2019 Project Leader: Tobin F. Hirsch ​ [email protected] Project Members: Matthew Meyers, Lucas Greenwich High School ​ Greenwich, CT Gazianis, John Trudeau, Zane Khader, [email protected] Rebecca Lytle, William Owens, Christina Keating, Zachary Mester and Delfina Gomez Contents Executive Summary.................................................................................................................................................................2 ​ Introduction..............................................................................................................................................................................2 ​ The Status Quo.........................................................................................................................................................................3 ​ Alternative Voting Systems......................................................................................................................................................7 ​ Criteria for an Effective Policy................................................................................................................................................8 ​ Evaluation of Reforms.............................................................................................................................................................9 ​ The Status Quo............................................................................................................................................................9
    [Show full text]
  • 5.4. Instant-Runoff Voting
    Formal Verification of Voting Schemes Diploma Thesis by Michael Kirsten Department of Informatics Institute of Theoretical Informatics (ITI) Application-oriented Formal Verification Supervisor: Prof. Dr. rer. nat. Bernhard Beckert Advisors: Dipl.-Inform. Thorsten Bormer Prof. Dr. Rajeev Goré December 21, 2014 KIT – University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz Association www.kit.edu Abstract Fundamental trust and credibility in democratic systems is commonly established through the existence and execution of democratic elections. The vote-counting of an election, usually formalised by a voting scheme, essentially boils down to a mechanism that aggregates individual preferences of the voters to reach a decision. For this matter, there are various differing voting schemes in use throughout the world, commonly based on high expectations and means to ensure a sensible democratic process. However, incidents such as the ruling by the German federal constitutional court which led to a change of the German legislation in 2013 manifest that it is difficult for a voting scheme to meet these legitimate expectations [BGB13]. In fact, there is no general notion of correctness for a voting scheme and thus no universal mechanism as shown in Kenneth J. Arrow’s Impossibility Theorem in 1951 [Arr51]. As a consequence, designing a real-world voting scheme without flaws, which still gives significant democratic guarantees, is a difficult task as a trade-off between desirable properties is non-trivial and error-prone. The approach in this thesis is based on the idea to tackle this issue by proposing an incremental and iterative development process for voting schemes based on automated formal reasoning methods using program verification.
    [Show full text]
  • Weak Mutual Majority Criterion for Voting Rules
    Weak Mutual Majority Criterion for Voting Rules Aleksei Yu. Kondratev1 and Alexander S. Nesterov2 1 Higher School of Economics, Kantemirovskaya 3, 194100 St.Petersburg, Russia [email protected] 2 Higher School of Economics, Kantemirovskaya 3, 194100 St.Petersburg, Russia [email protected] Abstract We study a novel axiom for voting rules: the weak mutual majority criterion (WMM). A voting rule satisfies WMM if whenever some k candidates receive top k ranks from a qualified majority that consists of more than q = k=(k+1) of voters, the rule selects the winner among these k candidates. WMM lies between the two standard axioms: it is stronger than the majority criterion (here k = 1 and q = 1=2) and weaker than the mutual majority criterion (MM, here for any k the size of majority is fixed q = 1=2). The widespread plurality rule satisfies WMM (but not MM). Moreover, for any k the bound q = k=(k + 1) is tight. The plurality with runoff rule, the Dodgson's rule, the Condorcet least reversal rule, the Simpson's rule, and the Young's rule satisfy WMM, for most of these rules we also find tight bounds on the size of the qualified majority q. The well-known Black's rule and its positional version do not satisfy WMM: for k > 1 its tight bound q = 1. We propose two modifications of the Black's positional rule that satisfy WMM: the qualified mutual majority rule with the tight bound q = k=(k + 1) and the convex median voting rule with the tight bound q = (3k − 1)=(4k).
    [Show full text]