DOCSLIB.ORG

5.4. Instant-Runoff Voting

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
5.4. Instant-Runoff Voting Formal Verification of Voting Schemes Diploma Thesis by Michael Kirsten Department of Informatics Institute of Theoretical Informatics (ITI) Application-oriented Formal Verification Supervisor: Prof. Dr. rer. nat. Bernhard Beckert Advisors: Dipl.-Inform. Thorsten Bormer Prof. Dr. Rajeev Goré December 21, 2014 KIT – University of the State of Baden-Wuerttemberg and National Research Center of the Helmholtz Association www.kit.edu Abstract Fundamental trust and credibility in democratic systems is commonly established through the existence and execution of democratic elections. The vote-counting of an election, usually formalised by a voting scheme, essentially boils down to a mechanism that aggregates individual preferences of the voters to reach a decision. For this matter, there are various differing voting schemes in use throughout the world, commonly based on high expectations and means to ensure a sensible democratic process. However, incidents such as the ruling by the German federal constitutional court which led to a change of the German legislation in 2013 manifest that it is difficult for a voting scheme to meet these legitimate expectations [BGB13]. In fact, there is no general notion of correctness for a voting scheme and thus no universal mechanism as shown in Kenneth J. Arrow’s Impossibility Theorem in 1951 [Arr51]. As a consequence, designing a real-world voting scheme without flaws, which still gives significant democratic guarantees, is a difficult task as a trade-off between desirable properties is non-trivial and error-prone. The approach in this thesis is based on the idea to tackle this issue by proposing an incremental and iterative development process for voting schemes based on automated formal reasoning methods using program verification. We analyse two different forms of verification considering their role in this development process in order to achieve formal correctness of voting schemes. We perform a comprehensive set of case studies by applying “medium-weight” and “light-weight” verification techniques. The “medium- weight” approach uses the annotation-based deductive verification tool VCC based on an auto-active methodology and the “light-weight” technique is performed with the bounded model checking tool LLBMC. Our analysis covers a set of well-known voting schemes combined with a set of prominent voting scheme criteria. In addition to giving precise formalisations for these criteria adapted to the specific voting schemes and tools used, we advance the efficiency of the “light-weight” approach by exploiting fundamental symmetric properties. Furthermore, we investigate on encountered challenges posed by the auto-active verification methodology, which lies in-between automatic and interactive verification methodologies, with respect to specific characteristics in voting schemes and also explore the potential of bounded verification techniques to produce precise counterexamples in order to enhance the capability of our envisioned development process to give early feedback. This thesis gives fundamental insights in general challenges and the potential of automated formal reasoning with the goal of correct voting schemes. Deutsche Zusammenfassung Ein großer Teil des Vertrauens und der Glaubwürdigkeit in demokratischen Systemen wird gemeinhin durch das Abhalten und den Ablauf von demokratischen Wahlen geschaffen. Die Entscheidungsfindung einer Wahl, gewöhnlich durch ein Wahlverfahren formalisiert, ist im Kern ein Mechanismus zur Aggregation individueller Wählerpräferenzen auf ein Wahlergebnis. Für diese Aufgabe wird eine Vielzahl unterschiedlicher Wahlverfahren in vielen Ländern der Erde angewandt, die üblicherweise auf hohen gesellschaftlichen Ansprüchen basieren um einen angemessenen demokratischen Prozess sicherzustellen. Jedoch zeigen Vorfälle wie das Urteil des Bundesverfassungsgerichts der Bundesrepu- blik Deutschland, das 2013 zu einer Änderung der deutschen Verfassung führte, dass es schwierig ist, ein Wahlverfahren zu finden, dass diese berechtigten Erwartungen er- füllt [BGB13]. In der Tat existiert keine allgemein gültige Auffassung von Korrektheit für ein Wahlverfahren und in der Konsequenz auch keine universelle Prozedur, wie schon Kenneth J. Arrow 1951 in seinem Allgemeinen Unmöglichkeitstheorem zeigte [Arr51]. Daraus ergibt sich, dass der Entwurf eines realistischen fehlerfreien Wahlverfahrens, das dennoch angemessene demokratische Zusicherungen gibt, eine schwierige Aufgabe ist, da ein Ausgleich zwischen wünschenswerten Eingenschaften fehleranfällig und nicht trivial ist. Das Vorgehen dieser Arbeit um diesen Missstand anzugehen basiert auf der Idee ei- nes stufenweisen und iterativen Entwicklungsprozesses für Wahlsysteme basierend auf automatischen formal-logischen Beweisverfahren. Es werden zwei verschiedene Beweis- techniken bezüglich ihrer Rolle in diesem Entwicklungsprozess analysiert, um formale Korrektheit für Wahlverfahren zu erreichen. Dabei wird eine umfassende Fallstudie durch- geführt, bei der verschiedene Verifikationstechniken, die wir als “leichtgewichtig” und “mittel-gewichtig” klassifizieren, zur Anwendung kommen. Der “mittelschwere” Ansatz wird durch das annotationsbasierte deduktive Verifikationswerkzeug VCC unterstützt, das auf einer auto-aktiven Methodik basiert und die “leichtgewichtige” Technik nutzt das Werkzeug LLBMC zur beschränkten Modellprüfung (bounded model checking). Die Ana- lyse beinhaltet bekannte Wahlverfahren kombiniert mit allgemeinen Korrektheitskriterien für Wahlverfahren. Über die Aufstellung präziser Formalisierungen dieser Kriterien ange- passt auf die spezifischen Wahlverfahren hinaus wird die Effizienz des “leichtgewichtigen” Ansatzes durch die Ausnutzung fundamentaler Symmetrieeigenschaften vorangebracht. Außerdem untersucht diese Arbeit Herausforderungen, die sich aus der auto-aktiven Me- thodik bezüglich bestimmter Charakteristika von Wahlverfahren ergeben, und erkundet das Potential von Verifikationstechniken innerhalb bestimmter Grenzen bezüglich der Eingabegrößen, präzise Gegenbeispiele zu generieren, um den langfristig angestrebten Ent- wicklungsprozess um die Möglichkeit zu erweitern, frühzeitige Rückmeldungen bezüglich der Korrektheit zu geben. Diese Arbeit erarbeitet fundamentale Einsichten in allgemeine vi Herausforderungen und das Potential automatisierter formal-logischer Beweisverfahren bezüglich korrekter Wahlverfahren. Acknowledgements I would like to thank Prof. Dr. Bernhard Beckert and Prof. Dr. Rajeev Goré for giving me the opportunity to be part of this exciting project and the experiences gained during my visit at the Australian National University (ANU) in Canberra, Australia. Great thanks go especially to Prof. Dr. Bernhard Beckert for supporting my work during my visit and beyond, including lots of productive and motivating discussions. A special thanks goes to my advisor Thorsten Bormer for taking the time for me, having lots of patience, motivating me and many lively debates supporting my work. Last but not least, I want to thank my parents for all the support for me and my studies over the years. Statement of Authorship I declare that I have developed and written the enclosed thesis completely by myself, and have not used sources or means without declaration in the text. Karlsruhe, December 21, 2014 .......................................... (Michael Kirsten) Contents 1. Introduction 1 1.1. Research Objectives . .2 1.2. Correctness of Voting Schemes . .2 1.3. Outline . .3 2. Voting Schemes and Correctness Properties 5 2.1. A General Definition of Voting Schemes . .5 2.2. Arrow’s Impossibility Theorem and its Implications . .7 2.3. Selected Voting Schemes . .9 2.3.1. Plurality Voting . 10 2.3.2. Approval Voting . 12 2.3.3. Instant-Runoff Voting . 13 2.3.4. Single Transferable Vote . 17 2.4. Selected Voting Scheme Properties . 17 2.4.1. Monotonicity Criterion . 19 2.4.2. Condorcet Winner and Loser Criteria . 21 3. Techniques and Tools for Verification 25 3.1. Selected Verification Techniques . 25 3.1.1. Auto-Active Deductive Program Verification . 26 3.1.2. Software Bounded Model Checking . 28 3.2. Selected Verification Tools . 29 3.2.1. Deductive Verification with VCC . 29 3.2.2. Bounded Verification with LLBMC . 33 4. Deductive Verification of Plurality Voting with VCC 35 4.1. FPTP Implementation and Specification of Monotonicity Criterion . 35 4.2. Full Verification with Auxiliary Specifications . 39 4.3. Simplifying the Specification with Loop Unrolling . 46 5. Bounded Verification with LLBMC and Counterexample Generation 51 5.1. General Setup and Encoding . 51 5.2. Plurality Voting . 54 5.3. Approval Voting . 58 5.4. Instant-Runoff Voting . 60 5.5. Single Transferable Vote . 66 5.6. Summary . 70 xii Contents 5.7. Generation of Counterexamples . 72 5.7.1. Instant-Runoff Voting . 72 5.7.2. Single Transferable Vote . 75 6. Improving Performance of Bounded Verification by Symmetry Reduction 79 6.1. Plurality Voting with Anonymity . 79 6.2. Plurality Voting with Anonymity and Neutrality . 83 6.3. Approval Voting with Anonymity and Neutrality . 85 7. Conclusion 89 7.1. Related Work . 89 7.2. Summary and Results . 90 7.3. Outlook and Future Work . 92 A. Implementations and Specifications 93 A.1. Plurality Voting for VCC . 93 A.1.1. Full Specification of Monotonicity for Plurality Voting . 93 A.1.2. Lemma for Monotonicity Criterion . 96 A.2. Plurality Voting for LLBMC . 97 A.2.1. General Plurality Voting . 98 A.2.2. FPTP with Symmetry Breaking Predicates for Anonymity . 99 A.2.3. FPTP with Predicates for Anonymity and Neutrality . 101 A.3. Approval Voting for LLBMC
Load more

Recommended publications
  • Are Condorcet and Minimax Voting Systems the Best?1
    1 Are Condorcet and Minimax Voting Systems the Best?1 Richard B. Darlington Cornell University Abstract For decades, the minimax voting system was well known to experts on voting systems, but was not widely considered to be one of the best systems. But in recent years, two important experts, Nicolaus Tideman and Andrew Myers, have both recognized minimax as one of the best systems. I agree with that. This paper presents my own reasons for preferring minimax. The paper explicitly discusses about 20 systems. Comments invited. [email protected] Copyright Richard B. Darlington May be distributed free for non-commercial purposes Keywords Voting system Condorcet Minimax 1. Many thanks to Nicolaus Tideman, Andrew Myers, Sharon Weinberg, Eduardo Marchena, my wife Betsy Darlington, and my daughter Lois Darlington, all of whom contributed many valuable suggestions. 2 Table of Contents 1. Introduction and summary 3 2. The variety of voting systems 4 3. Some electoral criteria violated by minimax’s competitors 6 Monotonicity 7 Strategic voting 7 Completeness 7 Simplicity 8 Ease of voting 8 Resistance to vote-splitting and spoiling 8 Straddling 8 Condorcet consistency (CC) 8 4. Dismissing eight criteria violated by minimax 9 4.1 The absolute loser, Condorcet loser, and preference inversion criteria 9 4.2 Three anti-manipulation criteria 10 4.3 SCC/IIA 11 4.4 Multiple districts 12 5. Simulation studies on voting systems 13 5.1. Why our computer simulations use spatial models of voter behavior 13 5.2 Four computer simulations 15 5.2.1 Features and purposes of the studies 15 5.2.2 Further description of the studies 16 5.2.3 Results and discussion 18 6.
    [Show full text]
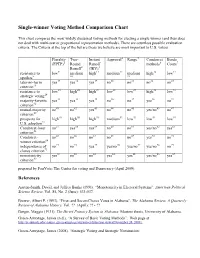
  • Single-Winner Voting Method Comparison Chart
    Single-winner Voting Method Comparison Chart This chart compares the most widely discussed voting methods for electing a single winner (and thus does not deal with multi-seat or proportional representation methods). There are countless possible evaluation criteria. The Criteria at the top of the list are those we believe are most important to U.S. voters. Plurality Two- Instant Approval4 Range5 Condorcet Borda (FPTP)1 Round Runoff methods6 Count7 Runoff2 (IRV)3 resistance to low9 medium high11 medium12 medium high14 low15 spoilers8 10 13 later-no-harm yes17 yes18 yes19 no20 no21 no22 no23 criterion16 resistance to low25 high26 high27 low28 low29 high30 low31 strategic voting24 majority-favorite yes33 yes34 yes35 no36 no37 yes38 no39 criterion32 mutual-majority no41 no42 yes43 no44 no45 yes/no 46 no47 criterion40 prospects for high49 high50 high51 medium52 low53 low54 low55 U.S. adoption48 Condorcet-loser no57 yes58 yes59 no60 no61 yes/no 62 yes63 criterion56 Condorcet- no65 no66 no67 no68 no69 yes70 no71 winner criterion64 independence of no73 no74 yes75 yes/no 76 yes/no 77 yes/no 78 no79 clones criterion72 81 82 83 84 85 86 87 monotonicity yes no no yes yes yes/no yes criterion80 prepared by FairVote: The Center for voting and Democracy (April 2009). References Austen-Smith, David, and Jeffrey Banks (1991). “Monotonicity in Electoral Systems”. American Political Science Review, Vol. 85, No. 2 (June): 531-537. Brewer, Albert P. (1993). “First- and Secon-Choice Votes in Alabama”. The Alabama Review, A Quarterly Review of Alabama History, Vol. ?? (April): ?? - ?? Burgin, Maggie (1931). The Direct Primary System in Alabama.
    [Show full text]
  • Legislature by Lot: Envisioning Sortition Within a Bicameral System
    PASXXX10.1177/0032329218789886Politics & SocietyGastil and Wright 789886research-article2018 Special Issue Article Politics & Society 2018, Vol. 46(3) 303 –330 Legislature by Lot: Envisioning © The Author(s) 2018 Article reuse guidelines: Sortition within a Bicameral sagepub.com/journals-permissions https://doi.org/10.1177/0032329218789886DOI: 10.1177/0032329218789886 System* journals.sagepub.com/home/pas John Gastil Pennsylvania State University Erik Olin Wright University of Wisconsin–Madison Abstract In this article, we review the intrinsic democratic flaws in electoral representation, lay out a set of principles that should guide the construction of a sortition chamber, and argue for the virtue of a bicameral system that combines sortition and elections. We show how sortition could prove inclusive, give citizens greater control of the political agenda, and make their participation more deliberative and influential. We consider various design challenges, such as the sampling method, legislative training, and deliberative procedures. We explain why pairing sortition with an elected chamber could enhance its virtues while dampening its potential vices. In our conclusion, we identify ideal settings for experimenting with sortition. Keywords bicameral legislatures, deliberation, democratic theory, elections, minipublics, participation, political equality, sortition Corresponding Author: John Gastil, Department of Communication Arts & Sciences, Pennsylvania State University, 232 Sparks Bldg., University Park, PA 16802, USA. Email: [email protected] *This special issue of Politics & Society titled “Legislature by Lot: Transformative Designs for Deliberative Governance” features a preface, an introductory anchor essay and postscript, and six articles that were presented as part of a workshop held at the University of Wisconsin–Madison, September 2017, organized by John Gastil and Erik Olin Wright.
    [Show full text]
  • Single Transferable Vote Resists Strategic Voting
    Single Transferable Vote Resists Strategic Voting John J. Bartholdi, III School of Industrial and Systems Engineering Georgia Institute of Technology, Atlanta, GA 30332 James B. Orlin Sloan School of Management Massachusetts Institute of Technology, Cambridge, MA 02139 November 13, 1990; revised April 4, 2003 Abstract We give evidence that Single Tranferable Vote (STV) is computation- ally resistant to manipulation: It is NP-complete to determine whether there exists a (possibly insincere) preference that will elect a favored can- didate, even in an election for a single seat. Thus strategic voting under STV is qualitatively more difficult than under other commonly-used vot- ing schemes. Furthermore, this resistance to manipulation is inherent to STV and does not depend on hopeful extraneous assumptions like the presumed difficulty of learning the preferences of the other voters. We also prove that it is NP-complete to recognize when an STV elec- tion violates monotonicity. This suggests that non-monotonicity in STV elections might be perceived as less threatening since it is in effect “hid- den” and hard to exploit for strategic advantage. 1 1 Strategic voting For strategic voting the fundamental problem for any would-be manipulator is to decide what preference to claim. We will show that this modest task can be impractically difficult under the voting scheme known as Single Transferable Vote (STV). Furthermore this difficulty pertains even in the ideal situation in which the manipulator knows the preferences of all other voters and knows that they will vote their complete and sincere preferences. Thus STV is apparently unique among voting schemes in actual use today in that it is computationally resistant to manipulation.
    [Show full text]
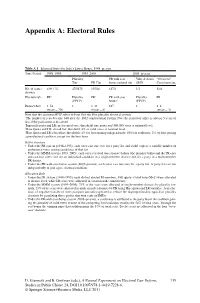
  • Appendix A: Electoral Rules
    Appendix A: Electoral Rules Table A.1 Electoral Rules for Italy’s Lower House, 1948–present Time Period 1948–1993 1993–2005 2005–present Plurality PR with seat Valle d’Aosta “Overseas” Tier PR Tier bonus national tier SMD Constituencies No. of seats / 6301 / 32 475/475 155/26 617/1 1/1 12/4 districts Election rule PR2 Plurality PR3 PR with seat Plurality PR (FPTP) bonus4 (FPTP) District Size 1–54 1 1–11 617 1 1–6 (mean = 20) (mean = 6) (mean = 4) Note that the acronym FPTP refers to First Past the Post plurality electoral system. 1The number of seats became 630 after the 1962 constitutional reform. Note the period of office is always 5 years or less if the parliament is dissolved. 2Imperiali quota and LR; preferential vote; threshold: one quota and 300,000 votes at national level. 3Hare Quota and LR; closed list; threshold: 4% of valid votes at national level. 4Hare Quota and LR; closed list; thresholds: 4% for lists running independently; 10% for coalitions; 2% for lists joining a pre-electoral coalition, except for the best loser. Ballot structure • Under the PR system (1948–1993), each voter cast one vote for a party list and could express a variable number of preferential votes among candidates of that list. • Under the MMM system (1993–2005), each voter received two separate ballots (the plurality ballot and the PR one) and cast two votes: one for an individual candidate in a single-member district; one for a party in a multi-member PR district. • Under the PR-with-seat-bonus system (2005–present), each voter cast one vote for a party list.
    [Show full text]
  • Canvasser's Manual
    STV MESSAGE TESTING: CANVASSER’S MANUAL CONTENTS 1 INTRODUCTION ....................................................................................................................................... 2 1.1 BACKGROUND ........................................................................................................................................... 2 1.2 CASELOAD SUMMARY ................................................................................................................................. 2 1.3 CONTACTS ................................................................................................................................................ 2 2 THE “TREATMENTS” ................................................................................................................................ 3 2.1 THE MESSAGES .......................................................................................................................................... 3 2.2 THE ENDORSERS ........................................................................................................................................ 4 2.3 THE PLACEBO TREATMENT ........................................................................................................................... 4 3 DAILY DOCUMENTS ................................................................................................................................. 5 3.1 DAILY SHEETS ...........................................................................................................................................
    [Show full text]
  • Ranked-Choice Voting from a Partisan Perspective
    Ranked-Choice Voting From a Partisan Perspective Jack Santucci December 21, 2020 Revised December 22, 2020 Abstract Ranked-choice voting (RCV) has come to mean a range of electoral systems. Broadly, they can facilitate (a) majority winners in single-seat districts, (b) majority rule with minority representation in multi-seat districts, or (c) majority sweeps in multi-seat districts. Such systems can be combined with other rules that encourage/discourage slate voting. This paper describes five major versions used in U.S. public elections: Al- ternative Vote (AV), single transferable vote (STV), block-preferential voting (BPV), the bottoms-up system, and AV with numbered posts. It then considers each from the perspective of a `political operative.' Simple models of voting (one with two parties, another with three) draw attention to real-world strategic issues: effects on minority representation, importance of party cues, and reasons for the political operative to care about how voters rank choices. Unsurprisingly, different rules produce different outcomes with the same votes. Specific problems from the operative's perspective are: majority reversal, serving two masters, and undisciplined third-party voters (e.g., `pure' independents). Some of these stem from well-known phenomena, e.g., ballot exhaus- tion/ranking truncation and inter-coalition \vote leakage." The paper also alludes to vote-management tactics, i.e., rationing nominations and ensuring even distributions of first-choice votes. Illustrative examples come from American history and comparative politics. (209 words.) Keywords: Alternative Vote, ballot exhaustion, block-preferential voting, bottoms- up system, exhaustive-preferential system, instant runoff voting, ranked-choice voting, sequential ranked-choice voting, single transferable vote, strategic coordination (10 keywords).
    [Show full text]
  • The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity 3
    Working Paper The Expanding Approvals Rule: Improving Proportional Representation and Monotonicity Haris Aziz · Barton E. Lee Abstract Proportional representation (PR) is often discussed in voting settings as a major desideratum. For the past century or so, it is common both in practice and in the academic literature to jump to single transferable vote (STV) as the solution for achieving PR. Some of the most prominent electoral reform movements around the globe are pushing for the adoption of STV. It has been termed a major open prob- lem to design a voting rule that satisfies the same PR properties as STV and better monotonicity properties. In this paper, we first present a taxonomy of proportional representation axioms for general weak order preferences, some of which generalise and strengthen previously introduced concepts. We then present a rule called Expand- ing Approvals Rule (EAR) that satisfies properties stronger than the central PR axiom satisfied by STV, can handle indifferences in a convenient and computationally effi- cient manner, and also satisfies better candidate monotonicity properties. In view of this, our proposed rule seems to be a compelling solution for achieving proportional representation in voting settings. Keywords committee selection · multiwinner voting · proportional representation · single transferable vote. JEL Classification: C70 · D61 · D71 1 Introduction Of all modes in which a national representation can possibly be constituted, this one [STV] affords the best security for the intellectual qualifications de- sirable in the representatives—John Stuart Mill (Considerations on Represen- tative Government, 1861). arXiv:1708.07580v2 [cs.GT] 4 Jun 2018 H. Aziz · B. E. Lee Data61, CSIRO and UNSW, Sydney 2052 , Australia Tel.: +61-2-8306 0490 Fax: +61-2-8306 0405 E-mail: [email protected], [email protected] 2 Haris Aziz, Barton E.
    [Show full text]
  • Woman's Position, Preference Voting, and the Election of Women
    WOMAN’S POSITION, PREFERENCE VOTING, AND THE ELECTION OF WOMEN: Why Are Women Less Likely to Enjoy Electoral Success in List PR Systems with Preference Voting Compared to Closed List Voting? Maarja Lühiste University of Exeter [email protected] ABSTRACT: Previous literature suggests that women are less likely to enjoy individual electoral success and overall descriptive representation in list PR systems that employ preference voting as opposed to closed list voting. One of the main explanations to this phenomenon is that it is easier to convince party gatekeepers than voters of the importance of women’s representation. This research puts this hypothesis to test relying on unique individual level data from the 2009 European Elections. I demonstrate with the 2009 European Election Study Candidate Survey and Media Content Data that (i) it is important to distinguish between open list and ordered list preference voting, (ii) women do not fare worse in all types of preference voting systems compared to closed list voting systems, and (iii) the reason why women fare worse in certain types of preference voting systems compared to closed list system is not because voters do not vote for women but because party-gatekeepers position female candidates in lower list positions in ordered list systems compared to closed list systems. This article therefore demonstrates that there are differences in ‘viable’ candidate selection in different voting systems, which in turn affects the likelihood of women’s electoral success and descriptive representation in general. Paper prepared for the “ELECDEM” closing conference in Florence, IT, June 28-30, 2012. 1 INTRODUCTION There are fewer women than men in nearly all democratically elected legislative bodies around the world.
    [Show full text]
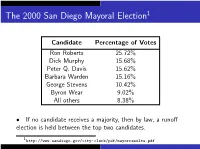
  • The Plurality-With-Elimination Method (PWE)
    The 2000 San Diego Mayoral Election1 Candidate Percentage of Votes Ron Roberts 25.72% Dick Murphy 15.68% Peter Q. Davis 15.62% Barbara Warden 15.16% George Stevens 10.42% Byron Wear 9.02% All others 8.38% • If no candidate receives a majority, then by law, a runoff election is held between the top two candidates. 1http://www.sandiego.gov/city-clerk/pdf/mayorresults.pdf Example: The 2000 San Diego Mayoral Election Practical problems with this system: I Runoff elections cost time and money I Ties (or near-ties) for second place I Preference ballots provide a method of holding an “instant-runoff" election: the Plurality-with-Elimination Method (PWE). 2. If no candidate has received a majority, then eliminate the candidate with the fewest first-place votes. 3. Repeat steps 1 and 2 until some candidate has a majority, then declare that candidate the winner. The Plurality-with-Elimination Method (x1.4) 1. Count the first-place votes. If some candidate receives a majority of the first-place votes, then that candidate is the winner. 3. Repeat steps 1 and 2 until some candidate has a majority, then declare that candidate the winner. The Plurality-with-Elimination Method (x1.4) 1. Count the first-place votes. If some candidate receives a majority of the first-place votes, then that candidate is the winner. 2. If no candidate has received a majority, then eliminate the candidate with the fewest first-place votes. The Plurality-with-Elimination Method (x1.4) 1. Count the first-place votes. If some candidate receives a majority of the first-place votes, then that candidate is the winner.
    [Show full text]
  • The Alternative Vote : in Theory and Practice
    Edith Cowan University Research Online Theses : Honours Theses 2004 The Alternative Vote : In Theory and Practice Vanessa Beckingham Edith Cowan University Follow this and additional works at: https://ro.ecu.edu.au/theses_hons Part of the Election Law Commons Recommended Citation Beckingham, V. (2004). The Alternative Vote : In Theory and Practice. https://ro.ecu.edu.au/theses_hons/ 952 This Thesis is posted at Research Online. https://ro.ecu.edu.au/theses_hons/952 Edith Cowan University Copyright Warning You may print or download ONE copy of this document for the purpose of your own research or study. The University does not authorize you to copy, communicate or otherwise make available electronically to any other person any copyright material contained on this site. You are reminded of the following: Copyright owners are entitled to take legal action against persons who infringe their copyright. A reproduction of material that is protected by copyright may be a copyright infringement. A court may impose penalties and award damages in relation to offences and infringements relating to copyright material. Higher penalties may apply, and higher damages may be awarded, for offences and infringements involving the conversion of material into digital or electronic form. THE ALTERNATIVE VOTE: IN THEORY AND PRACTICE BY VANESSA BECKINGHAM BA (ARTS) A thesis submitted in the partial fulfillment of the requirements for the award of Bachelor of Arts (Politics and Government) with Honours Faculty of Community Services, Education and Social Sciences Edith Cowan University Date of Submission: II March 2004 USE OF THESIS The Use of Thesis statement is not included in this version of the thesis.
    [Show full text]
  • Arrow's Impossibility Theorem
    Arrow’s Impossibility Theorem Some announcements • Final reflections due on Monday. • You now have all of the methods and so you can begin analyzing the results of your election. Today’s Goals • We will discuss various fairness criteria and how the different voting methods violate these criteria. Last Time We have so far discussed the following voting methods. • Plurality Method (Majority Method) • Borda Count Method • Plurality-with-Elimination Method (IRV) • Pairwise Comparison Method • Method of Least Worst Defeat • Ranked Pairs Method • Approval Voting Fairness Criteria The following fairness criteria were developed by Kenneth Arrow, an economist in the 1940s. Economists are often interested in voting theories because of their impact on game theory. The mathematician John Nash (the subject of A Beautiful Mind) won the Nobel Prize in economics for his contributions to game theory. The Majority Criterion A majority candidate should always be the winner. Note that this does not say that a candidate must have a majority to win, only that such a candidate should not lose. Plurality, IRV, Pairwise Comparison, LWD, and Ranked Pairs all satisfy the Majority Criterion. The Majority Criterion The Borda Count Method violates the Majority Criterion. Number of voters 6 2 3 1st A B C 2nd B C D 3rd C D B 4th D A A Even though A had a majority of votes it only has 29 points. B is the winner with 32 points. Moral: Borda Count punishes polarizing candidates. The Condorcet Criterion A Condorcet candidate should always be the winner. Recall that a Condorcet Candidate is one that beats all other candidates in a head-to-head (pairwise) comparison.
    [Show full text]