DOCSLIB.ORG

Gibbs Paradox: Mixing and Non Mixing Potentials T

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Gibbs Paradox: Mixing and Non Mixing Potentials T Physics Education 1 Jul - Sep 2016 Gibbs paradox: Mixing and non mixing potentials T. P. Suresh 1∗, Lisha Damodaran 1 and K. M. Udayanandan 2 1 School of Pure and Applied Physics Kannur University, Kerala- 673 635, INDIA *[email protected] 2 Nehru Arts and Science College, Kanhangad Kerala- 671 314, INDIA (Submitted 12-03-2016, Revised 13-05-2016) Abstract Entropy of mixing leading to Gibbs paradox is studied for different physical systems with and without potentials. The effect of potentials on the mixing and non mixing character of physical systems is discussed. We hope this article will encourage students to search for new problems which will help them understand statistical mechanics better. 1 Introduction namics of any system (which is the main aim of statistical mechanics) we need to calculate Statistical mechanics is the study of macro- the canonical partition function, and then ob- scopic properties of a system from its mi- tain macro properties like internal energy, en- croscopic description. In the ensemble for- tropy, chemical potential, specific heat, etc. malism introduced by Gibbs[1] there are of the system from the partition function. In three ensembles-micro canonical, canonical this article we make use of the canonical en- and grand canonical ensemble. Since we are semble formalism to study the extensive char- not interested in discussing quantum statis- acter of entropy and then to calculate the tics we will use the canonical ensemble for in- entropy of mixing. It is then used to ex- troducing our ideas. To study the thermody- plain the Gibbs paradox. Most text books Volume 32, Number 3, Article Number: 4. www.physedu.in Physics Education 2 Jul - Sep 2016 [2, 3, 4, 5, 6, 7, 8, 9] discuss Gibbs paradox in the denominator of the partition function. considering only the case of the classical ideal The corrected N particle partition function gas, but here we analyze different physical is QN systems with and without potentials. The Q = 1 ; study of Gibbs paradox is very fundamental N N! as pointed out by Erwin Schrdinger- \ It has where Q1 is the single particle partition func- always been believed that Gibbs paradox em- tion. bodied profound thought. That it was inti- With this correction the entropy become mately linked up with something so impor- extensive which resolves the paradox. tant and entirely new could hardly have been foreseen." V 5 S = N k ln + : N λ3 2 2 Gibbs paradox The entropy of mixing then turns out to be When entropy of an ideal gas was calculated V1 + V2 ∆S =k (N1 + N2) ln using ensemble theory, it was found to be not N1 + N2 extensive. V1 V2 − k N1 ln + N2 ln : V 3 N1 N2 S = N k ln + : λ3 2 If the initial particle densities of two similar The entropy of mixing for two ideal gases is mixing systems are equal, this equation gives the difference between the total entropy after ∆S = 0. The recipe of Gibbs corrects the mixing and that of individual systems before enumeration of micro states as necessitated mixing. For the same particle density, the by the indistinguishability of identical parti- entropy of mixing is given by cles [3]. N1 + N2 N1 + N2 ∆S = k N1 ln + N2 ln : N1 N2 3 Thermodynamics in If we find ∆S for two different ideal gases it is the canonical ensemble found that there is a finite entropy of mixing, but a paradoxical situation is there for sim- In the canonical ensemble the bridging equa- ilar ones - instead of getting ∆S = 0 there tion to find the thermodynamics is is a finite entropy of mixing. Thus the non extensive character of the entropy equation A = −kT ln QN ; causes the Gibbs paradox when there is mix- ing. This paradox is resolved in an ad hoc where A is the Helmholtz free energy, k is way by Gibbs. He put a correction factor N! Boltzmann's constant and T is the absolute Volume 32, Number 3, Article Number: 4. www.physedu.in Physics Education 3 Jul - Sep 2016 temperature. To circumvent Gibbs paradox 1. Non-relativistic free particles the above equation is modified as 2. Massive particles with a relativistic for- QN mulation A = −kT ln : N! 3. Ultra relativistic Using Stirling's approximation, ln N! = N ln N − N; 4.1 Non-relativistic A = −kT (ln Q − N ln N + N) : N For a single non-relativistic particle, the en- With the inclusion of Gibbs' correction factor ergy is p2 A contains new terms which are T and N E = dependent. So the entropy (S) given by the 2m equation and the N particle partition function is @A S = − V N @T Q = ; V;N N λ3 needs to be modified. In the coming sections we will consider different systems with and where V is the volume and λ is the de Broglie with out potentials which can be grouped in thermal wavelength given by to mixing and non mixing systems as relevent h to the Gibbs paradox. The systems are clas- λ = 1 : sified as (2πm kT ) 2 1. Free classical particles The entropy is V 3 2. Particles in a potential without Gibbs S = N k ln 3 + paradox λ 2 3. Particles in a potential with Gibbs para- which is not extensive. Introducing the Gibbs correction factor 1 in the N particle parti- dox N! tion function we get In these sections we will connect the effect N of potentials on entropy of mixing by finding 1 V QN = the extensive nature of entropy for different N! λ3 physical systems. and entropy becomes V 5 S = N k ln + (1) 4 Free classical particles N λ3 2 Free particles can be which is extensive. Volume 32, Number 3, Article Number: 4. www.physedu.in Physics Education 4 Jul - Sep 2016 4.2 Massive particles with a Using this partition function if we calculate relativistic formulation the entropy we will get it as not extensive but intensive. Introducing the Gibbs correction For relativistic particles the energy is factor the entropy becomes p 2 2 2 4 p = p c + m c V S = Nk ln 3 + 4 : For massive particles mc2 pc and the par- Nλr tition function is which is clearly extensive. N The above calculations show that all types of V 2 Q = e−β m c ; N λ3 free particles exhibit the Gibbs paradox if the Gibbs correction factor is not used. 1 where β = kT ; and the entropy is V 2 3 N S = Nk ln e−β m c + Nk + m c2 λ3 2 T 5 Particles in a potential which is not extensive. With the Gibbs cor- In the coming two sections we will check what rection factor the entropy becomes will be the effect of potentials in the sys- tem to the extensive character of entropy and V 5 S = N k ln + thereby to the Gibbs paradox. N λ3 2 which is same as in Eq.(1). 5.1 Particles in a potential without Gibbs paradox 4.3 Ultra relativistic 1. Particles in a harmonic potential 2 Here pc mc and the partition function is Consider an array of equally spaced N N harmonic oscillators along a finite length " 3# 8πV kT L with one particle per harmonic oscil- QN = : h3 c lator site. The Hamiltonian for a single particle is The de Broglie thermal wavelength is p2 1 hc H = + Kx2 λr = 1 : 2m 2 2π 3 kT So where K is the spring constant given V N by K = m!2, where m is the mass of Q = : N 3 the particles and ! its angular frequency. λr Volume 32, Number 3, Article Number: 4. www.physedu.in Physics Education 5 Jul - Sep 2016 The single particle partition function is The N particle partition function is p N 1 2 L=2 2 3 Z px Z Kx 1 πm 1 −β −β 4 Q1 = e 2m dpx e 2 dx QN = Γ 1 (2 kT ) : 4 4 h −∞ −L=2 2 hK r ! kT βKL2 = Erf The entropy is ~! 8 p 3 1 πm 3 4 S = Nk + ln Γ 1 (2 kT ) In the thermodynamic limit N, L ! 1 4 4 2 h K 4 and N=L is finite, the Erf(1) = 1, so which is extensive. for the infinite length the single particle partition function reduces to 3. Anharmonic oscillator For an anharmonic oscillator the Hamil- kT Q = tonian is 1 ! ~ p2 H = + Cq2 − gq3 − fq4 and then 2m where C, g and f are positive constants Q = (Q )N : N 1 but their values are very small. The N particle partition function is So the entropy is " 1 #N 2 kT 2m πkT S = N k 1 + ln ; QN = (X) ; ~! C h which is extensive even without Gibbs where correction factor. So there is no entropy 3kT f 5g2 X = 1 + + + :: : of mixing, and in this case the entropy 4 C2 4C3 is simply additive. The harmonic poten- tial bounds the particles in the system. The entropy is When two such systems are in contact " " 1 ## no particle flow happens from system to 2m 2 πkT S = Nk 1 + ln + Y; the other. Thus the harmonic potential C h makes the system non mixing. where 2. Quartic oscillator 3 f 5g2 For a quartic oscillator the Hamiltonian Y = Nk kT 2 + 3 + :: : is 2 C 4C p2 1 H = + Kq4: 2m 2 The entropy is extensive. Volume 32, Number 3, Article Number: 4. www.physedu.in Physics Education 6 Jul - Sep 2016 4. Electron in a magnetic field Consider a system of localized particles of spin half with magnetic moment µB, in the presence of an external magnetic field of strength B.
Load more

Recommended publications
  • Gibbs' Paradox and the Definition of Entropy
    Entropy 2008, 10, 15-18 entropy ISSN 1099-4300 °c 2008 by MDPI www.mdpi.org/entropy/ Full Paper Gibbs’ Paradox and the Definition of Entropy Robert H. Swendsen Physics Department, Carnegie Mellon University, Pittsburgh, PA 15213, USA E-Mail: [email protected] Received: 10 December 2007 / Accepted: 14 March 2008 / Published: 20 March 2008 Abstract: Gibbs’ Paradox is shown to arise from an incorrect traditional definition of the entropy that has unfortunately become entrenched in physics textbooks. Among its flaws, the traditional definition predicts a violation of the second law of thermodynamics when applied to colloids. By adopting Boltzmann’s definition of the entropy, the violation of the second law is eliminated, the properties of colloids are correctly predicted, and Gibbs’ Paradox vanishes. Keywords: Gibbs’ Paradox, entropy, extensivity, Boltzmann. 1. Introduction Gibbs’ Paradox [1–3] is based on a traditional definition of the entropy in statistical mechanics found in most textbooks [4–6]. According to this definition, the entropy of a classical system is given by the product of Boltzmann’s constant, k, with the logarithm of a volume in phase space. This is shown in many textbooks to lead to the following equation for the entropy of a classical ideal gas of distinguishable particles, 3 E S (E; V; N) = kN[ ln V + ln + X]; (1) trad 2 N where X is a constant. Most versions of Gibbs’ Paradox, including the one I give in this section, rest on the fact that Eq. 1 is not extensive. There is another version of Gibbs’ Paradox that involves the mixing of two gases, which I will discuss in the third section of this paper.
    [Show full text]
  • Gibb's Paradox for Distinguishable
    Gibb’s paradox for distinguishable K. M. Udayanandan1, R. K. Sathish1, A. Augustine2 1Department of Physics, Nehru Arts and Science College, Kerala-671 314, India. 2Department of Physics, University of Kannur, Kerala 673 635, India. E-mail: [email protected] (Received 22 March 2014, accepted 17 November 2014) Abstract Boltzmann Correction Factor (BCF) N! is used in micro canonical ensemble and canonical ensemble as a dividing term to avoid Gibbs paradox while finding the number of states and partition function for ideal gas. For harmonic oscillators this factor does not come since they are considered to be distinguishable. We here show that BCF comes twice for harmonic oscillators in grand canonical ensemble for entropy to be extensive in classical statistics. Then we extent this observation for all distinguishable systems. Keywords: Gibbs paradox, harmonic oscillator, distinguishable particles. Resumen El factor de corrección de Boltzmann (BCF) N! se utiliza en ensamble microcanónico y ensamble canónico como un término divisor para evitar la paradoja de Gibbs, mientras se busca el número de estados y la función de partición para un gas ideal. Para osciladores armónicos este factor no viene sin que éstos sean considerados para ser distinguibles. Mostramos aquí que BCF llega dos veces para osciladores armónicos en ensamble gran canónico para que la entropía sea ampliamente usada en la estadística clásica. Luego extendemos esta observación para todos los sistemas distinguibles. Palabras clave: paradoja de Gibbs, oscilador armónico, partículas distinguibles. PACS: 03.65.Ge, 05.20-y ISSN 1870-9095 I. INTRODUCTION Statistical mechanics is a mathematical formalism by which II. CANONICAL ENSEMBLE one can determine the macroscopic properties of a system from the information about its microscopic states.
    [Show full text]
  • Classical Particle Indistinguishability, Precisely
    Classical Particle Indistinguishability, Precisely James Wills∗1 1Philosophy, Logic and Scientific Method, London School of Economics Forthcoming in The British Journal for the Philosophy of Science Abstract I present a new perspective on the meaning of indistinguishability of classical particles. This leads to a solution to the problem in statisti- cal mechanics of justifying the inclusion of a factor N! in a probability distribution over the phase space of N indistinguishable classical par- ticles. 1 Introduction Considerations of the identity of objects have long been part of philosophical discussion in the natural sciences and logic. These considerations became particularly pertinent throughout the twentieth century with the develop- ment of quantum physics, widely recognized as having interesting and far- reaching implications concerning the identity, individuality, indiscernibility, indistinguishability1 of the elementary components of our ontology. This discussion continues in both the physics and philosophy literature2. ∗[email protected] 1. This menagerie of terms in the literature is apt to cause confusion, especially as there is no clear consensus on what exactly each of these terms mean. Throughout the rest of the paper, I will be concerned with giving a precise definition of a concept which I will label `indistinguishability', and which, I think, matches with how most other commentators use the word. But I believe it to be a distinct debate whether particles are `identical', `individual', or `indiscernible'. The literature I address in this paper therefore does not, for example, overlap with the debate over the status of Leibniz's PII. 2. See French (2000) for an introduction to this discussion and a comprehensive list of references.
    [Show full text]
  • Lecture 6: Entropy
    Matthew Schwartz Statistical Mechanics, Spring 2019 Lecture 6: Entropy 1 Introduction In this lecture, we discuss many ways to think about entropy. The most important and most famous property of entropy is that it never decreases Stot > 0 (1) Here, Stot means the change in entropy of a system plus the change in entropy of the surroundings. This is the second law of thermodynamics that we met in the previous lecture. There's a great quote from Sir Arthur Eddington from 1927 summarizing the importance of the second law: If someone points out to you that your pet theory of the universe is in disagreement with Maxwell's equationsthen so much the worse for Maxwell's equations. If it is found to be contradicted by observationwell these experimentalists do bungle things sometimes. But if your theory is found to be against the second law of ther- modynamics I can give you no hope; there is nothing for it but to collapse in deepest humiliation. Another possibly relevant quote, from the introduction to the statistical mechanics book by David Goodstein: Ludwig Boltzmann who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics. There are many ways to dene entropy. All of them are equivalent, although it can be hard to see. In this lecture we will compare and contrast dierent denitions, building up intuition for how to think about entropy in dierent contexts. The original denition of entropy, due to Clausius, was thermodynamic.
    [Show full text]
  • Gibbs Paradox of Entropy of Mixing: Experimental Facts, Its Rejection and the Theoretical Consequences
    ELECTRONIC JOURNAL OF THEORETICAL CHEMISTRY, VOL. 1, 135±150 (1996) Gibbs paradox of entropy of mixing: experimental facts, its rejection and the theoretical consequences SHU-KUN LIN Molecular Diversity Preservation International (MDPI), Saengergasse25, CH-4054 Basel, Switzerland and Institute for Organic Chemistry, University of Basel, CH-4056 Basel, Switzerland ([email protected]) SUMMARY Gibbs paradox statement of entropy of mixing has been regarded as the theoretical foundation of statistical mechanics, quantum theory and biophysics. A large number of relevant chemical and physical observations show that the Gibbs paradox statement is false. We also disprove the Gibbs paradox statement through consideration of symmetry, similarity, entropy additivity and the de®ned property of ideal gas. A theory with its basic principles opposing Gibbs paradox statement emerges: entropy of mixing increases continuously with the increase in similarity of the relevant properties. Many outstanding problems, such as the validity of Pauling's resonance theory and the biophysical problem of protein folding and the related hydrophobic effect, etc. can be considered on a new theoretical basis. A new energy transduction mechanism, the deformation, is also brie¯y discussed. KEY WORDS Gibbs paradox; entropy of mixing; mixing of quantum states; symmetry; similarity; distinguishability 1. INTRODUCTION The Gibbs paradox of mixing says that the entropy of mixing decreases discontinuouslywith an increase in similarity, with a zero value for mixing of the most similar or indistinguishable subsystems: The isobaric and isothermal mixing of one mole of an ideal ¯uid A and one mole of a different ideal ¯uid B has the entropy increment 1 (∆S)distinguishable = 2R ln 2 = 11.53 J K− (1) where R is the gas constant, while (∆S)indistinguishable = 0(2) for the mixing of indistinguishable ¯uids [1±10].
    [Show full text]
  • PHYS 521: Statistical Mechanics Homework #4
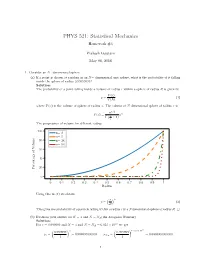
    PHYS 521: Statistical Mechanics Homework #4 Prakash Gautam May 08, 2018 1. Consider an N−dimensional sphere. (a) If a point is chosen at random in an N− dimensional unit sphere, what is the probability of it falling inside the sphere of radius 0:99999999? Solution: The probability of a point falling inside a volume of radius r within a sphere of radius R is given by V (r) p = (1) V (R) where V (x) is the volume of sphere of radius x. The volume of N dimensional sphere of radius x is n=2 (π ) n V (x) = n x Γ 2 + 1 The progression of volume for different radius. 100 n= 2 n= 5 80 n= 24 n= 54 60 40 20 Percentage of Volume 0 0 0:1 0:2 0:3 0:4 0:5 0:6 0:7 0:8 0:9 1 Radius Using this in (1) we obtain ( ) r n p = (2) R This gives the probability of a particle falling within a radius r in a Ndimensional sphere of radius R. □ (b) Evaluate your answer for N = 3 and N = NA(the Avogadro Number) Solution: 23 For r = 0:999999 and N = 3 and N = NA = 6:023 × 10 we get ( ) ( ) × 23 0:999999 3 0:999999 6:023 10 p = = 0:999997000003 p = = 0:0000000000000 3 1 NA 1 1 The probability of a particle falling within the radius nearly 1 in higher two-dimensional sphere is vanishningly small. □ (c) What do these results say about the equivalence of the definitions of entropy in terms of either of the total phase space volume of the volume of outermost energy shell? Solution: Considering a phase space volume bounded by E + ∆ where ∆ ≪ E.
    [Show full text]
  • A Note on Gibbs Paradox 1. Introduction
    1 A note on Gibbs paradox P. Radhakrishnamurty 282, Duo Marvel Layout, Anathapuragate, Yelahanka, Bangalore 560064, India. email: [email protected] Abstract We show in this note that Gibbs paradox arises not due to application of thermodynamic principles, whether classical or statistical or even quantum mechanical, but due to incorrect application of mathematics to the process of mixing of ideal gases. ------------------------------------------------------------------------------------------------------------------------------- Key Words: Gibbs paradox, Amagat’s law, Dalton’s law, Ideal gas mixtures, entropy change 1. Introduction ‘It has always been believed that Gibbs paradox embodied profound thought’, Schrodinger [1]. It is perhaps such a belief that underlies the continuing discussion of Gibbs paradox over the last hundred years or more. Literature available on Gibbs paradox is vast [1-15]. Lin [16] and Cheng [12] give extensive list of some of the important references on the issue, besides their own contributions. Briefly stated, Gibbs paradox arises in the context of application of the statistical mechanical analysis to the process of mixing of two ideal gas samples. The discordant values of entropy change associated with the process, in the two cases: 1. when the two gas samples contain the same species and, 2. when they contain two different species constitutes the gist of Gibbs paradox. A perusal of the history of the paradox shows us that: Boltzmann, through the application of statistical mechanics to the motion of particles (molecules) and the distribution of energy among the particles contained in a system, developed the equation: S = log W + S(0), connecting entropy S of the system to the probability W of a microscopic state corresponding to a given macroscopic equilibrium state of the system, S(0) being the entropy at 0K.
    [Show full text]
  • Dynamical Manifestation of Gibbs Paradox After a Quantum Quench
    Dynamical manifestation of Gibbs paradox after a quantum quench M. Collura1, M. Kormos2 and G. Takács2;3∗ 1The Rudolf Peierls Centre for Theoretical Physics, Oxford University, Oxford, OX1 3NP, United Kingdom 2BME “Momentum” Statistical Field Theory Research Group, H-1117 Budapest, Budafoki út 8. 3BME Department of Theoretical Physics, H-1117 Budapest, Budafoki út 8. (Dated: 29th September 2018) We study the propagation of entanglement after quantum quenches in the non-integrable para- magnetic quantum Ising spin chain. Tuning the parameters of the system, we observe a sudden increase in the entanglement production rate, which we show to be related to the appearance of new quasi-particle excitations in the post-quench spectrum. We argue that the phenomenon is the non- equilibrium version of the well-known Gibbs paradox related to mixing entropy and demonstrate that its characteristics fit the expectations derived from the quantum resolution of the paradox in systems with a non-trivial quasi-particle spectrum. I. INTRODUCTION parameter hx shows another kind of anomalous behav- ior: a sudden increase setting in at the threshold value of A quantum quench is a protocol routinely engineered hx where a new quasi-particle excitation appears in the in cold-atom experiments [1–9]: a sudden change of the spectrum. Hamiltonian of an isolated quantum system followed by Using the physical interpretation of the asymptotic en- a non-equilibrium time evolution. The initial state cor- tanglement of a large subsystem as the thermodynamic responds to a highly excited configuration of the post- entropy of the stationary (equilibrium) state [2, 12, 33, quench Hamiltonian, acting as a source of quasi-particle 37, 38], this can be recognized as arising from the con- excitations [10].
    [Show full text]
  • Mathematical Solution of the Gibbs Paradox V
    ISSN 0001-4346, Mathematical Notes, 2011, Vol. 89, No. 2, pp. 266–276. © Pleiades Publishing, Ltd., 2011. Original Russian Text © V. P. Maslov, 2011, published in Matematicheskie Zametki, 2011, Vol. 89, No. 2, pp. 272–284. Mathematical Solution of the Gibbs Paradox V. P. Maslov * Moscow State University Received December 20, 2010 Abstract—In this paper, we construct a new distribution corresponding to a real noble gas as well as the equation of state for it. DOI: 10.1134/S0001434611010329 Keywords: Zeno line, partitio numerorum, phase transition, cluster, dimer, critical tempera- ture, Boyle temperature, jamming effect, Bose–Einstein distribution, Gibbs paradox. Since all the papers of the author dealing with this problem1 were published in English, here we present a short survey of these papers in both Russian and English. The Gibbs paradox has been a stumbling block for many physicists, including Einstein, Gibbs, Planck, Fermi, and many others (15 Nobel laureates in physics studied this problem) as well as for two great mathematicians Von Neumann and Poincare.´ Poincare´ did not obtain the mathematical solution of the Gibbs paradox, but attempted to solve this problem from the philosophical point of view.2 A careful analysis of Poincare’s´ philosophy shows that it is especially constructed so as to justify the contradiction between two physical theories. He writes, in particular, “If a physicist finds a contradiction between two theories that are equally dear to him, he will sometimes say: let’s not worry about this; the intermediate links of the chain may be hidden from us, but we will strongly hold on to its extremities.
    [Show full text]
  • Statistical Physics University of Cambridge Part II Mathematical Tripos
    Preprint typeset in JHEP style - HYPER VERSION Statistical Physics University of Cambridge Part II Mathematical Tripos David Tong Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge, CB3 OBA, UK http://www.damtp.cam.ac.uk/user/tong/statphys.html [email protected] { 1 { Recommended Books and Resources • Reif, Fundamentals of Statistical and Thermal Physics A comprehensive and detailed account of the subject. It's solid. It's good. It isn't quirky. • Kardar, Statistical Physics of Particles A modern view on the subject which offers many insights. It's superbly written, if a little brief in places. A companion volume, \The Statistical Physics of Fields" covers aspects of critical phenomena. Both are available to download as lecture notes. Links are given on the course webpage • Landau and Lifshitz, Statistical Physics Russian style: terse, encyclopedic, magnificent. Much of this book comes across as remarkably modern given that it was first published in 1958. • Mandl, Statistical Physics This is an easy going book with very clear explanations but doesn't go into as much detail as we will need for this course. If you're struggling to understand the basics, this is an excellent place to look. If you're after a detailed account of more advanced aspects, you should probably turn to one of the books above. • Pippard, The Elements of Classical Thermodynamics This beautiful little book walks you through the rather subtle logic of classical ther- modynamics. It's very well done. If Arnold Sommerfeld had read this book, he would have understood thermodynamics the first time round.
    [Show full text]
  • The Gibbs Paradox: Early History and Solutions
    entropy Article The Gibbs Paradox: Early History and Solutions Olivier Darrigol UMR SPHere, CNRS, Université Denis Diderot, 75013 Paris, France; [email protected] Received: 9 April 2018; Accepted: 28 May 2018; Published: 6 June 2018 Abstract: This article is a detailed history of the Gibbs paradox, with philosophical morals. It purports to explain the origins of the paradox, to describe and criticize solutions of the paradox from the early times to the present, to use the history of statistical mechanics as a reservoir of ideas for clarifying foundations and removing prejudices, and to relate the paradox to broad misunderstandings of the nature of physical theory. Keywords: Gibbs paradox; mixing; entropy; irreversibility; thermochemistry 1. Introduction The history of thermodynamics has three famous “paradoxes”: Josiah Willard Gibbs’s mixing paradox of 1876, Josef Loschmidt reversibility paradox of the same year, and Ernst Zermelo’s recurrence paradox of 1896. The second and third revealed contradictions between the law of entropy increase and the properties of the underlying molecular dynamics. They prompted Ludwig Boltzmann to deepen the statistical understanding of thermodynamic irreversibility. The Gibbs paradox—first called a paradox by Pierre Duhem in 1892—denounced a violation of the continuity principle: the mixing entropy of two gases (to be defined in a moment) has the same finite value no matter how small the difference between the two gases, even though common sense requires the mixing entropy to vanish for identical gases (you do not really mix two identical substances). Although this paradox originally belonged to purely macroscopic thermodynamics, Gibbs perceived kinetic-molecular implications and James Clerk Maxwell promptly followed him in this direction.
    [Show full text]
  • Demonstration and Resolution of the Gibbs Paradox of the First Kind
    Demonstration and resolution of the Gibbs paradox of the first kind Hjalmar Peters Karlsruhe Institute of Technology, Karlsruhe, Germany E-mail: [email protected] Abstract. The Gibbs paradox of the first kind (GP1) refers to the false increase in entropy which, in statistical mechanics, is calculated from the process of combining two gas systems S1 and S2 consisting of distinguishable particles. Presented in a somewhat modified form, the GP1 manifests as a contradiction to the second law of thermodynamics. Contrary to popular belief, this contradiction affects not only classical but also quantum statistical mechanics. The present paper resolves the GP1 by considering two effects: 1. The uncertainty about which particles are located in S1 and which in S2 contributes to the entropies of S1 and S2. 2. S1 and S2 are correlated by the fact that if a certain particle is located in one system, it cannot be located in the other. As a consequence, the entropy of the total system consisting of S1 and S2 is not the sum of the entropies of S1 and S2. PACS numbers: 05.30.Ch, 05.30.-d, 05.20.-y arXiv:1306.4638v2 [cond-mat.stat-mech] 1 Oct 2013 Demonstration and resolution of the Gibbs paradox of the first kind 2 1. Introduction, motivation, and outline In physics, there are two distinct paradoxes which are both known as the \Gibbs paradox" and are often confused with each other. In the following, the false increase in entropy which, in statistical mechanics, is calculated from the process of combining two gases of the same kind consisting of distinguishable particles will be referred to as the Gibbs paradox of the first kind (GP1) [1{5].
    [Show full text]