DOCSLIB.ORG

Hydrophobic Effect, Water Structure, and Heat Capacity Changes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hydrophobic Effect, Water Structure, and Heat Capacity Changes J. Phys. Chem. B 1997, 101, 4343-4348 4343 Hydrophobic Effect, Water Structure, and Heat Capacity Changes Kim A. Sharp* and Bhupinder Madan Department of Biochemistry & Biophysics, UniVersity of PennsylVania, 3700 Hamilton Walk, Philadelphia, PennsylVania 19104-6059 ReceiVed: January 16, 1997; In Final Form: April 1, 1997X hyd The hydration heat capacity (∆Cp ) of nine solutes of varying hydrophobicity was studied using a combination of a random network model equation of water and Monte Carlo simulations. Nonpolar solutes cause a concerted decrease in the average length and angle of the water-water hydrogen bonds in the first hydration shell, while polar and ionic solutes have the opposite effect. This is due to changes in the amounts, relative to bulk water, of two populations of hydrogen bonds: one with shorter and more linear bonds and the other with longer and more bent bonds. Heat capacity changes were calculated from these changes in water structure using a random network model equation of state. The calculated changes account for observed hyd differences in ∆Cp for the various solutes. The simulations provide a unified picture of hydrophobic and hyd polar hydration, and both a structural and thermodynamic explanation of the opposite signs of ∆Cp observed for polar and nonpolar solutes. Introduction nonpolar groups means that at higher temperatures (T > 80 °C) their insolubility results from unfavorable changes in enthalpy, In recent years analysis of heat capacity changes has become not entropy. Second, the hydration of a majority of polar and of central importance in understanding the thermodynamics of ionic solutes is also accompanied by a decrease in entropy, and protein folding, protein-protein binding, protein-nucleic acid thus by some kind of structuring of water, but in this case binding, and the hydrophobic effect.1-7 There are several hyd 7,16-20 reasons for this. First, the improved sensitivity and accuracy ∆Cp is negative. Thus, analysis of Cp changes has of calorimeters has provided a wealth of heat capacity (Cp) data become essential for a full understanding of polar and nonpolar for these processes. Second, Cp relates the other three major hydration and the hydrophobic effect. hyd thermodynamic quantitiessenthalpy (H), entropy (S), and free In spite of the importance of ∆Cp changes in a wide range energy (G)sto each other of processes involving solutes, proteins, and nucleic acids, basic features remain unexplained at the molecular level. From the 2 2 ∂H ∂S ∂2G 〈∆H〉 data of Privalov and Gill the increase in heat capacity for Cp T T2 (1) nonpolar groups amounts to about 3 cal/(mol K) for each water ) ) )- 2 ) 2 ∂T ∂T ∂T kT in the first hydration shell or 20% of the total heat capacity of (i) (ii) (iii) (iv) a single water molecule. There is no clear picture of how an increase in water structure can give rise both to this remarkably where T is the temperature, k is Boltzmann’s constant, and 〈∆H2〉 hyd large positive ∆Cp for nonpolar solutes and yet result in a is the mean-squared fluctuation in enthalpy. These four hyd negative ∆Cp for polar and ionic groups. Explanations for equivalent definitions of Cp illustrate the diverse thermodynamic hyd the positive ∆C of hydrophobic hydration in terms of the implications for processes that involve changes in Cp. For p induction of more ordered water which is “melted” at increasing example, unfolding of many proteins is accompanied by a large temperatures15,21,22 do not explain the negative ∆Chyd for polar increase in Cp,1,2 implying (eqs 1i and 1ii) that the unfolding p and ionic groups. The latter phenomenon is perhaps the more entropy and enthalpy depend strongly on temperature and puzzling because the entropy of polar and ionic hydration is implying (eq 1iii) that the stability curve (∆Gunfold vs T) will usually negative. Thus, one deduces from eq 1ii that the be an inverted U-shape with the consequent possibility of both ordering of water induced by these solutes increases with heat and cold denaturation. Changes in Cp associated with increasing temperature. This runs counter to the general protein folding and binding come almost entirely from changes hyd expectation that it becomes harder to induce order (decrease in hydration heat capacity (∆Cp ) due to burial (desolvation) entropy) at higher temperatures. of polar and nonpolar groups.3,8,9 Burial of nonpolar groups Monte Carlo or molecular dynamics simulations of solutes also provides the dominant stabilizing interaction (the hydro- in water using standard water and solute potential functions have phobic interaction) in protein folding and binding.10,11 provided much structural and thermodynamic information about The hydrophobic interaction is driven by the low solubility hydration. However, calculation of ∆Chyd directly from such of nonpolar compounds in water due, at room temperature, to p simulations via eq 1 using standard water and solute potential the unfavorable decrease in the entropy (increase in structure) function appears to be impractical without prohibitive size and of the hydrating waters. This has been described in many 23 hyd ways: as “icelike structures”, icebergs, flickering clusters, length computer simulations. Even determination of ∆Cp clathrates, and pentagonal clusters.12-14 It has become clear, by the most robust approach, using eq 1i, requires taking the however, that a description in terms of entropic changes alone difference of a difference in mean enthalpy from at least four s does not explain the distinctive features of the hydrophobic separate simulations between pure water and water plus one 15 hyd solutesand evaluating this difference at two or more temper- effect. First, the large positive ∆Cp for solvation of hyd atures. Direct determination of ∆Cp from simulations is thus * To whom correspondence should be addressed. subject to considerably more statistical uncertainty than the X Abstract published in AdVance ACS Abstracts, May 1, 1997. determination of the hydration free energy or enthalpy. S1089-5647(97)00245-9 CCC: $14.00 © 1997 American Chemical Society 4344 J. Phys. Chem. B, Vol. 101, No. 21, 1997 Sharp and Madan Figure 1. (a) Definition of H-bond length, d, and angle, θ. (b) Hydrogen bond structure and heat capacity changes. The solid surface shows the rn dependence of the RN model incremental heat capacity ∆Cp (vertical axis) on the mean H-bond length, d, and the rms H-bond angle, θ (horizontal axes). Values of the bond length and angle (and the associated heat capacity change) for the first hydration shell of solutes obtained from Monte Carlo simulations are shown for the nonpolar (2), polar (9), and mixed ( ) H-bond classes. The solutes are water (W), argon (A), ethanol (E), methane (M), K+ (K), Cs+ (C), N-methylacetamide (N), tetramethylammonium× (T), I- (I), and benzene (B). (c) Linear regression analysis of H-bond length vs angle. hyd We show here how an equation of state for ∆Cp derived with contributions from H-bond bending, stretching, vibrations, from a random hydrogen-bond (H-bond) network model of water a zero point distortion term, and van der Waals interactions, bend strecth vib zpd vdw can be combined with simulations of water around solutes to Cp , Cp , Cp , Cp , and Cp , respectively. These five hyd provide statistically reliable estimates of ∆Cp . Application contributions, expressed as cal/K per mole of H-bonds, are given of this approach to nine solutes of varying hydrophobicity by provides a unified description of hydrophobic, polar and ionic bend -θ2/2 -5.41θ2 hydration that explains at a molecular level how ordering of Cp ) 0.139e + 1.51e (3) water around solutes can result in either an increase or a decrease in Cp. stretch 2 Cp ) 2.10(1 - 3.72x) - 45.88σ (4) Theory and Methods 6 kFi Fi Fi kFi Fi vib Cp ) 0.9936T∑ coth( ) - ( - ) (5) The random network (RN) model is based on the observation 2 i)1 T T Fi T T that liquid water retains much of the tetrahedral H-bonding [ 2 ] T sinh ( ) network of ice I, albeit in a randomly distorted form due to T thermal fluctuations, and that the essential features of this 2 network can be described in terms of just three structural Czpd ) 0.235e-1.240θ -2.79x (6) parameters: the mean and standard deviation in H-bond length, p d, and s, respectively, and the root-mean-square (rms) H-bond 0.242e-θ 1 1 angle, θ.24,25 The H-bond length and angle used in the RN Cvdw p ) ( 12 - 6) + model are defined in Figure 1a. The RN model provides an θ (1 + x) (1 + x) accurate description of the structure of pure liquid water in terms 6 12 0.558(1 e-θ) (7) - ( 7 - 13) of the oxygen-oxygen radial distribution function, and it (1 + x) (1 + x) reproduces subtle properties of water, such as the bulk dielectric constant over the range 283-573 K, with remarkable where accuracy.26-28 The RN model also provides good equations of state for the free energy, enthalpy and entropy of pure liquid hνi -1.24θ2-2.79x -0.381hνi -1.24θ2-2.79x 26-28 F ) e , kF ) e (8) water over a wide range of temperatures, from which one i 2k i 2000k can derive an equation of state for the heat capacity in terms of the H-bond structural parameters23 where the mean and standard deviation in H-bond length are expressed in dimensionless form as x ) (d - 2.75)/2.75 and σ2 2 2 Crn(d,s,θ) ) Cbend(d,s,θ) + Cstretch(d,s,θ) + Cvib(d,s,θ) + ) [(s/2.75) + x ], respectively, h is Planck’s constant, and νi p p p p -1 zpd vdw ) 555, 660, 840, 60, 230, and 315 cm for i ) 1-6, Cp (d,s,θ) + Cp (d,s,θ) (2) respectively, are the reference frequencies of the three transla- Hydration Heat Capacity Simulations J.
Load more

Recommended publications
  • Heterogeneous Impacts of Protein-Stabilizing Osmolytes On
    bioRxiv preprint doi: https://doi.org/10.1101/328922; this version posted May 23, 2018. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Heterogeneous Impacts of Protein-Stabilizing Osmolytes on Hydrophobic Interaction Mrinmoy Mukherjee and Jagannath Mondal⇤ Tata Institute of Fundamental Research Hyderabad, 500107 India E-mail: [email protected],+914020203091 Abstract Osmolytes’ mechanism of protecting proteins against denaturation is a longstanding puzzle, further complicated by the complex diversities inherent in protein sequences. An emergent approach in understanding osmolytes’ mechanism of action towards biopoly- mer has been to investigate osmolytes’ interplay with hydrophobic interaction, the ma- jor driving force of protein folding. However, the crucial question is whether all these protein-stabilizing osmolytes display a single unified mechanism towards hydrophobic interactions. By simulating the hydrophobic collapse of a macromolecule in aqueous solutions of two such osmoprotectants, Glycine and Trimethyl N-oxide (TMAO), both of which are known to stabilize protein’s folded conformation, we here demonstrate that these two osmolytes can impart mutually contrasting effects towards hydropho- bic interaction. While TMAO preserves its protectant nature across diverse range of polymer-osmolyte interactions, glycine is found to display an interesting cross-over from being a protectant at weaker polymer-osmolyte interaction to a denaturant of hydrophobicity at stronger polymer-osmolyte interactions. A preferential-interaction analysis reveals that a subtle balance of conformation-dependent exclusion/binding of ⇤To whom correspondence should be addressed 1 bioRxiv preprint doi: https://doi.org/10.1101/328922; this version posted May 23, 2018.
    [Show full text]
  • Protein Structure & Folding
    6 Protein Structure & Folding To understand protein folding In the last chapter we learned that proteins are composed of amino acids Goal as a chemical equilibrium. linked together by peptide bonds. We also learned that the twenty amino acids display a wide range of chemical properties. In this chapter we will see Objectives that how a protein folds is determined by its amino acid sequence and that the three-dimensional shape of a folded protein determines its function by After this chapter, you should be able to: the way it positions these amino acids. Finally, we will see that proteins fold • describe the four levels of protein because doing so minimizes Gibbs free energy and that this minimization structure and the thermodynamic involves both making the most favorable bonds and maximizing disorder. forces that stabilize them. • explain how entropy (S) and enthalpy Proteins exhibit four levels of structure (H) contribute to Gibbs free energy. • use the equation ΔG = ΔH – TΔS The structure of proteins can be broken down into four levels of to determine the dependence of organization. The first is primary structure, the linear sequence of amino the favorability of a reaction on acids in the polypeptide chain. By convention, the primary sequence is temperature. written in order from the amino acid at the N-terminus (by convention • explain the hydrophobic effect and its usually on the left) to the amino acid at the C-terminus. The second level role in protein folding. of protein structure, secondary structure, is the local conformation adopted by stretches of contiguous amino acids.
    [Show full text]
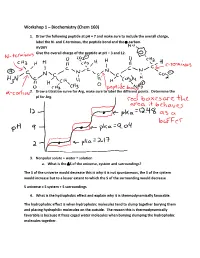
  • Workshop 1 – Biochemistry (Chem 160)
    Workshop 1 – Biochemistry (Chem 160) 1. Draw the following peptide at pH = 7 and make sure to include the overall charge, label the N- and C-terminus, the peptide bond and the -carbon. AVDKY Give the overall charge of the peptide at pH = 3 and 12. 2. Draw a titration curve for Arg, make sure to label the different points. Determine the pI for Arg. 3. Nonpolar solute + water = solution a. What is the S of the universe, system and surroundings? The S of the universe would decrease this is why it is not spontaneous, the S of the system would increase but to a lesser extent to which the S of the surrounding would decrease S universe = S system + S surroundings 4. What is the hydrophobic effect and explain why it is thermodynamically favorable. The hydrophobic effect is when hydrophobic molecules tend to clump together burying them and placing hydrophilic molecules on the outside. The reason this is thermodynamically favorable is because it frees caged water molecules when burying clumping the hydrophobic molecules together. 5. Urea dissolves very readily in water, but the solution becomes very cold as the urea dissolves. How is this possible? Urea dissolves in water because when dissolving there is a net increase in entropy of the universe. The heat exchange, getting colder only reflects the enthalpy (H) component of the total energy change. The entropy change is high enough to offset the enthalpy component and to add up to an overall -G 6. A mutation that changes an alanine residue in the interior of a protein to valine is found to lead to a loss of activity.
    [Show full text]
  • Biological Membranes
    14 Biological Membranes To understand the structure The fundamental unit of life is the cell. All living things are composed of Goal and composition of biological cells, be it a single cell in the case of many microorganisms or a highly membranes. organized ensemble of myriad cell types in the case of multicellular organisms. A defining feature of the cell is a membrane, the cytoplasmic Objectives membrane, that surrounds the cell and separates the inside of the cell, the After this chapter, you should be able to cytoplasm, from other cells and the extracellular milieu. Membranes also • distinguish between cis and trans surround specialized compartments inside of cells known as organelles. unsaturated fatty acids. Whereas cells are typically several microns (μm) in diameter (although • explain why phospholipids some cells can be much larger), the membrane is only about 10 nanometers spontaneously form lipid bilayers and (nm) thick. Yet, and as we will see in subsequent chapters, the membrane is sealed compartments. not simply an ultra-thin, pliable sheet that encases the cytoplasm. Rather, • describe membrane fluidity and how it membranes are dynamic structures that mediate many functions in the is affected by membrane composition life of the cell. In this chapter we examine the composition of membranes, and temperature. their assembly, the forces that stabilize them, and the chemical and physical • explain the role of cholesterol in properties that influence their function. buffering membrane fluidity. The preceding chapters have focused on two kinds of biological molecules, • explain how the polar backbone namely proteins and nucleic acids, that are important in the workings of a membrane protein can be accommodated in a bilayer.
    [Show full text]
  • Hydrophobic Catalysis and a Potential Biological Role of DNA Unstacking Induced by Environment Effects
    Hydrophobic catalysis and a potential biological role of DNA unstacking induced by environment effects Bobo Fenga,1, Robert P. Sosab,c,d, Anna K. F. Mårtenssona, Kai Jiange, Alex Tongf, Kevin D. Dorfmang, Masayuki Takahashih, Per Lincolna, Carlos J. Bustamanteb,c,d,f,i,j,k,l, Fredrik Westerlunde, and Bengt Nordéna,1 aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, 412 96 Gothenburg, Sweden; bBiophysics Graduate Group, University of California, Berkeley, CA 94720; cJason L. Choy Laboratory of Single Molecule Biophysics, University of California, Berkeley, CA 94720; dInstitute for Quantitative Biosciences-QB3, University of California, Berkeley, CA 94720; eDepartment of Biology and Biological Engineering, Chalmers University of Technology, 412 96 Gothenburg, Sweden; fDepartment of Chemistry, University of California, Berkeley, CA 94720; gDepartment of Chemical Engineering and Materials Science, University of Minnesota, Twin Cities, Minneapolis, MN 55455; hSchool of Life Science and Technology, Tokyo Institute of Technology, Tokyo 152-8550, Japan; iDepartment of Molecular & Cell Biology, University of California, Berkeley, CA 94720; jDepartment of Physics, University of California, Berkeley, CA 94720; kHoward Hughes Medical Institute, University of California, Berkeley, CA 94720; and lKavli Energy Nanosciences Institute, University of California, Berkeley, CA 94720 Edited by Feng Zhang, Broad Institute, Cambridge, MA, and approved July 22, 2019 (received for review May 27, 2019) Hydrophobic base stacking
    [Show full text]
  • Peptides & Proteins
    Peptides & Proteins (thanks to Hans Börner) 1 Proteins & Peptides Proteuos: Proteus (Gr. mythological figure who could change form) proteuo: „"first, ref. the basic constituents of all living cells” peptos: „Cooked referring to digestion” Proteins essential for: Structure, metabolism & cell functions 2 Bacterium Proteins (15 weight%) 50% (without water) • Construction materials Collagen Spider silk proteins 3 Proteins Structural proteins structural role & mechanical support "cell skeleton“: complex network of protein filaments. muscle contraction results from action of large protein assemblies Myosin und Myogen. Other organic material (hair and bone) are also based on proteins. Collagen is found in all multi cellular animals, occurring in almost every tissue. • It is the most abundant vertebrate protein • approximately a quarter of mammalian protein is collagen 4 Proteins Storage Various ions, small molecules and other metabolites are stored by complexation with proteins • hemoglobin stores oxygen (free O2 in the blood would be toxic) • iron is stored by ferritin Transport Proteins are involved in the transportation of particles ranging from electrons to macromolecules. • Iron is transported by transferrin • Oxygen via hemoglobin. • Some proteins form pores in cellular membranes through which ions pass; the transport of proteins themselves across membranes also depends on other proteins. Beside: Regulation, enzymes, defense, functional properties 5 Our universal container system: Albumines 6 zones: IA, IB, IIA, IIB, IIIA, IIIB; IIB and
    [Show full text]
  • Predicting Hydrophobic Alkyl-Alkyl and Perfluoroalkyl-Perfluoroalkyl Van
    Predicting hydrophobic alkyl-alkyl and perfluoroalkyl-perfluoroalkyl van der Waals dispersion interactions and their potential involvement in protein folding and the binding of drugs in hydrophobic pockets Clifford Fong To cite this version: Clifford Fong. Predicting hydrophobic alkyl-alkyl and perfluoroalkyl-perfluoroalkyl van der Waals dispersion interactions and their potential involvement in protein folding and the binding of drugs in hydrophobic pockets. [Research Report] Eigenenergy, Adelaide, Australia. 2019. hal-02176023v2 HAL Id: hal-02176023 https://hal.archives-ouvertes.fr/hal-02176023v2 Submitted on 5 Jan 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Predicting hydrophobic alkyl-alkyl and perfluoroalkyl-perfluoroalkyl van der Waals dispersion interactions and their potential involvement in protein folding and the binding of drugs in hydrophobic pockets Clifford W. Fong Eigenenergy, Adelaide, South Australia. Email: [email protected] Abstract It has been shown that a model compound which has previously allowed the experimental determination of the hydrophobic van der Waals dispersion alkyl-alkyl folding free energy interaction in a wide range of polar and non-polar solvents is strongly correlated with the cavitation, dispersion, solvent-structure (CDS) solvation free energy and to a lesser extent the molecular polarizability of the foldamers.
    [Show full text]
  • Probing the Base Stacking Contributions During
    PROBING THE BASE STACKING CONTRIBUTIONS DURING TRANSLESION DNA SYNTHESIS by BABHO DEVADOSS Submitted in partial fulfillment of the requirements For the degree of Doctor of Philosophy Thesis Adviser: Dr. Irene Lee Department of Chemistry CASE WESTERN RESERVE UNIVERSITY January, 2009 CASE WESTERN RESERVE UNIVERSITY SCHOOL OF GRADUATE STUDIES We hereby approve the thesis/dissertation of _____________________________________________________ candidate for the ______________________degree *. (signed)_______________________________________________ (chair of the committee) ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ ________________________________________________ (date) _______________________ *We also certify that written approval has been obtained for any proprietary material contained therein. ii TABLE OF CONTENTS Title Page…………………………………………………………………………………..i Committee Sign-off Sheet………………………………………………………………...ii Table of Contents…………………………………………………………………………iii List of Tables…………………………………………………………………………….vii List of Figures…………………………………………………………………….………ix Acknowledgements…………………………………………………………….………..xiv List of Abbreviations…………………………………………………………….………xv Abstract………………………………………………………………………………….xix CHAPTER 1 Introduction…………………………………………………………………1 1.1 The Chemistry and Biology of DNA…………………………………………2 1.2 DNA Synthesis……………………………………………………………….6 1.3 Structural Features of DNA Polymerases…………………………………...11
    [Show full text]
  • The Hydrophobic Effect Oil and Water Do Not Mix. This Fact Is So Well
    The hydrophobic effect Oil and water do not mix. This fact is so well engrained in our ever-day experience that we never ask “why”. Well, today we are going to ask just this question: “why do oil and water not mix?” At the end of the class you will hopefully see that the reason oil and water do not mix is quite distinct from the reason many other substance do not mix. You will also see that the hydrophobic effect is part of a family of processes called “entropy driven ordering” and that the hydrophobic effect has nothing to do with bonds between hydrophobic molecules. This should sound a bit strange to you right now, but I am sure that at the end of the class it will all make sense to you. Why most liquids mix or do not mix (the generic case) What would our physico-chemical intuition tell us about the process of mixing two liquids? Lets think of a simple lattice model for the two solutions. If we call the substances A and B, the energy for mixing should then be the energy of interaction that are made between A and B, minus the energy of interactions that A made with A, and B made with B, plus the entropy of mixing. "Gmixing = "Hmixing # T"Smixing where "Hmixing = 2"Ha#b # "Ha#a # "Hb#b What predictions would this simple model for solutions make for the energetics of mixing? First, mixing should be favored by entropy and therefore the tendency to mix ! should increase with temperature.
    [Show full text]
  • Characterizing Hydrophobicity of Amino Acid Side Chains in a Protein Environment Via Measuring Contact Angle of a Water Nanodroplet on Planar Peptide Network
    Characterizing hydrophobicity of amino acid side chains in a protein environment via measuring contact angle of a water nanodroplet on planar peptide network Chongqin Zhua,b,1, Yurui Gaoa,1, Hui Lic,d,1, Sheng Mengc,d,e, Lei Lia, Joseph S. Franciscoa,2, and Xiao Cheng Zenga,b,2 aDepartment of Chemistry, University of Nebraska−Lincoln, Lincoln, NE 68588; bBeijing Advanced Innovation Center for Soft Matter Science and Engineering, Beijing University of Chemical Technology, Beijing 100029, China; cBeijing National Laboratory for Condensed Matter Physics, Chinese Academy of Sciences, Beijing 100190, China; dInstitute of Physics, Chinese Academy of Sciences, Beijing 100190, China; and eCollaborative Innovation Center of Quantum Matter, Beijing 100190, China Contributed by Joseph S. Francisco, September 30, 2016 (sent for review September 1, 2016; reviewed by Liem Dang and Wei Yang) Hydrophobicity of macroscopic planar surface is conventionally char- of water droplets on the surface. This conventional method is not acterized by the contact angle of water droplets. However, this feasible for proteins, however, due to its high curvature and nano- engineering measurement cannot be directly extended to surfaces of scale size (38–40). Because of this experimental limitation, instead proteins, due to the nanometer scale of amino acids and inherent of measuring CA, researchers have developed other indirect nonplanar structures. To measure the hydrophobicity of side chains of methods to characterize relative hydrophobicity of amino acid proteins quantitatively, numerous parameters were developed to residues. One of widely used methods is based on a partition of characterize behavior of hydrophobic solvation. However, consistency amino acids in two immiscible liquid phases (8–16).
    [Show full text]
  • The Hydrogen Bond and Its Surroundings Part 2. the Hydrophobic-Bond-Myth
    Chem-Bio Informatics Journal, Vol.18, pp.10-20 (2018) Myths in Modern Science: The Hydrogen Bond and its Surroundings Part 2. The Hydrophobic-Bond-Myth Motohiro Nishio The CHPI Institute, 794-7-910 Izusan, Atami, Shizuoka, Japan E-mail [email protected] (Received September 19; accepted November 29, 2017; published online January 30, 2018) Abstract The fashionable but stereotypic thinking on the concept of the so-called “hydrophobic bond” has been examined in light of criticisms raised by many scientists: Hildebrand, Shinoda, Israelachvili, and so on. The author’s comments are given on the harmful influence of the concept of “hydrophobic bond” in chemistry and biochemistry. In my opinion, this concept can be considered as a myth in modern science. Key Words: proteins, hydrogen bond, nonpolar side-chain, Gibbs free energy Area of Interest: In silico drug discovery 10 Licensed under a Creative Commons Attribution 4.0 International(CC BY 4.0) Chem-Bio Informatics Journal, Vol.18, pp.10-20 (2018) 1. What is the Hydrophobic Bond? They were like two drops of oil that have dripped on to the surface of a basin of water. The drops gathered in one place by repelling water; it is more accurate to say that the pressure of water forces them to adhere to each other, making it impossible for either to get away. The above phrases come from Natsume Soseki’s1 novel “Mon,” The Gate.2 In this context we realize that water pushes oil molecules to adhere to each other, but not that oil molecules dislike water.
    [Show full text]
  • 48 September 25, 2017 Biochemistry I II. ______/ 4 BI/CH 421/621 III
    NAME _______________________________ Exam I I. _________________/48 September 25, 2017 Biochemistry I II. _________________/ 4 BI/CH 421/621 III. _________________/26 IV. _________________/22 TOTAL ________________/100 I. MULTIPLE CHOICE. (48 points; 2 pts each) Choose the BEST answer to the question by circling the appropriate letter. 1. The strength of hydrogen bonds, electrostatic interactions, and the values of the pKas of ionizable amino acid residues could be different in proteins than in aqueous solution because ____. A. water forms a clathrate structure around proteins B. proteins are hydrophilic on the inside and hydrophobic on the outside C. the entropy of the water increases when proteins fold up D. the microenvironment inside proteins could be different than in solution 2. Phosphoric acid is tribasic, with pKas of 2.14, 6.86, and 12.4. The ionic form that predominates at pH 3.2 is: A. H PO . - 2- 3- 3 4 B. H2PO4 . C. HPO4 . D. PO4 . 3. As the phase changes from water to ice, the decreased density of the water is due to: A. the loss of hydrogen bonds B. the gain of ionic bonds C. the gain of more van der Waals contacts D. the spacial arrangement of the assymetrical water molecules as they form the maximum number of hydrogen bonds possible E. the hydrophobic effect, which is driven by electrostatic interactions 4. In a mixture of the five proteins listed below, which should elute second in size-exclusion (gel filtration) chromatography? A. cytochrome c, Mr = 13,000 B. immunoglobulin G, Mr = 145,000 C. ribonuclease A, Mr = 13,700 D.
    [Show full text]