A Study of Perceptual Development for Musical Tuning
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
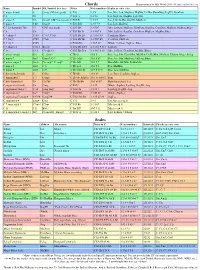
Chords and Scales 30/09/18 3:21 PM
Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø -

3 Manual Microtonal Organ Ruben Sverre Gjertsen 2013
3 Manual Microtonal Organ http://www.bek.no/~ruben/Research/Downloads/software.html Ruben Sverre Gjertsen 2013 An interface to existing software A motivation for creating this instrument has been an interest for gaining experience with a large range of intonation systems. This software instrument is built with Max 61, as an interface to the Fluidsynth object2. Fluidsynth offers possibilities for retuning soundfont banks (Sf2 format) to 12-tone or full-register tunings. Max 6 introduced the dictionary format, which has been useful for creating a tuning database in text format, as well as storing presets. This tuning database can naturally be expanded by users, if tunings are written in the syntax read by this instrument. The freely available Jeux organ soundfont3 has been used as a default soundfont, while any instrument in the sf2 format can be loaded. The organ interface The organ window 3 MIDI Keyboards This instrument contains 3 separate fluidsynth modules, named Manual 1-3. 3 keysliders can be played staccato by the mouse for testing, while the most musically sufficient option is performing from connected MIDI keyboards. Available inputs will be automatically recognized and can be selected from the menus. To keep some of the manuals silent, select the bottom alternative "to 2ManualMicroORGANircamSpat 1", which will not receive MIDI signal, unless another program (for instance Sibelius) is sending them. A separate menu can be used to select a foot trigger. The red toggle must be pressed for this to be active. This has been tested with Behringer FCB1010 triggers. Other devices could possibly require adjustments to the patch. -

Day 17 AP Music Handout, Scale Degress.Mus
Scale Degrees, Chord Quality, & Roman Numeral Analysis There are a total of seven scale degrees in both major and minor scales. Each of these degrees has a name which you are required to memorize tonight. 1 2 3 4 5 6 7 1 & w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic A triad can be built upon each scale degree. w w w w & w w w w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic The quality and scale degree of the triads is shown by Roman numerals. Captial numerals are used to indicate major triads with lowercase numerals used to show minor triads. Diminished triads are lowercase with a "degree" ( °) symbol following and augmented triads are capital followed by a "plus" ( +) symbol. Roman numerals written for a major key look as follows: w w w w & w w w w w w w w CM: wI (M) iiw (m) wiii (m) IV (M) V (M) vi (m) vii° (dim) I (M) EVERY MAJOR KEY FOLLOWS THE PATTERN ABOVE FOR ITS ROMAN NUMERALS! Because the seventh scale degree in a natural minor scale is a whole step below tonic instead of a half step, the name is changed to subtonic, rather than leading tone. Leading tone ALWAYS indicates a half step below tonic. Notice the change in the qualities and therefore Roman numerals when in the natural minor scale. -

Practical Music Theory – Book 1 by Pete Ford Table of Contents
Practical Music Theory – Book 1 by Pete Ford Table of Contents Preface xi About This Book Series xii To the Instructor xii Acknowledgements xii Part One Chapter 1: Notation 1 Clefs 1 The Grand Staff 2 Notes 2 Rests 3 Note Names 4 Rhythm 5 Simple Time 6 Dotted Notes in Simple Time 7 Compound Time 8 Subdivision in Compound Time 10 The Phrase Marking, Slur and the Tie 12 The Tie in Simple Time 12 The Tie in Compound Time 13 Repeat Signs, da Capo, and More 14 Assignment 1-1: Name the Notes 19 Assignment 1-2: Simple Time 21 Assignment 1-3: Compound Time 23 Chapter 2: Key Signatures 25 Writing Accidental Signs 25 The Cycle of Fourths 26 Key Signatures with Flats 27 Key Signatures with Sharps 28 Enharmonic Keys 30 Assignment 2-1: Name the Key Signature 33 Assignment 2-2: Key Signatures 35 Table of Contents Chapter 3: Building Scales 37 Writing the Major Scale 38 Introduction to Solfege 39 The Relative Minor Scale 40 The Cycle with Minor Keys Added 41 Writing the Natural Minor Scale 41 Solfege in Minor Keys 42 The Harmonic Minor Scale 44 The Melodic Minor Scale 46 Assignment 3-1: Write the Scales #1 49 Assignment 3-2: Write the Scales #2 51 Chapter 4: Intervals 53 Primary Intervals of the Major Scale 53 Writing Ascending Intervals 55 Writing Descending Intervals 57 Playing Intervals on the Piano 59 Hearing and Singing Intervals 59 Secondary Intervals 60 Writing Descending Secondary Intervals 62 Assignment 4-1: Write the Intervals 65 Assignment 4-2: Secondary Intervals 67 Part Two Chapter 5: Building Chords (SATB) 71 Triads of the Major Scale -

Consonance and Dissonance in Visual Music Bill Alves Harvey Mudd College
Claremont Colleges Scholarship @ Claremont All HMC Faculty Publications and Research HMC Faculty Scholarship 8-1-2012 Consonance and Dissonance in Visual Music Bill Alves Harvey Mudd College Recommended Citation Bill Alves (2012). Consonance and Dissonance in Visual Music. Organised Sound, 17, pp 114-119 doi:10.1017/ S1355771812000039 This Article is brought to you for free and open access by the HMC Faculty Scholarship at Scholarship @ Claremont. It has been accepted for inclusion in All HMC Faculty Publications and Research by an authorized administrator of Scholarship @ Claremont. For more information, please contact [email protected]. Organised Sound http://journals.cambridge.org/OSO Additional services for Organised Sound: Email alerts: Click here Subscriptions: Click here Commercial reprints: Click here Terms of use : Click here Consonance and Dissonance in Visual Music Bill Alves Organised Sound / Volume 17 / Issue 02 / August 2012, pp 114 - 119 DOI: 10.1017/S1355771812000039, Published online: 19 July 2012 Link to this article: http://journals.cambridge.org/abstract_S1355771812000039 How to cite this article: Bill Alves (2012). Consonance and Dissonance in Visual Music. Organised Sound, 17, pp 114-119 doi:10.1017/ S1355771812000039 Request Permissions : Click here Downloaded from http://journals.cambridge.org/OSO, IP address: 134.173.130.244 on 24 Jul 2014 Consonance and Dissonance in Visual Music BILL ALVES Harvey Mudd College, The Claremont Colleges, 301 Platt Blvd, Claremont CA 91711 USA E-mail: [email protected] The concepts of consonance and dissonance broadly Plato found the harmony of the world in the Pythag- understood can provide structural models for creators of orean whole numbers and their ratios, abstract ideals visual music. -

Major and Minor Scales Half and Whole Steps
Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale. -

Helmholtz's Dissonance Curve
Tuning and Timbre: A Perceptual Synthesis Bill Sethares IDEA: Exploit psychoacoustic studies on the perception of consonance and dissonance. The talk begins by showing how to build a device that can measure the “sensory” consonance and/or dissonance of a sound in its musical context. Such a “dissonance meter” has implications in music theory, in synthesizer design, in the con- struction of musical scales and tunings, and in the design of musical instruments. ...the legacy of Helmholtz continues... 1 Some Observations. Why do we tune our instruments the way we do? Some tunings are easier to play in than others. Some timbres work well in certain scales, but not in others. What makes a sound easy in 19-tet but hard in 10-tet? “The timbre of an instrument strongly affects what tuning and scale sound best on that instrument.” – W. Carlos 2 What are Tuning and Timbre? 196 384 589 amplitude 787 magnitude sample: 0 10000 20000 30000 0 1000 2000 3000 4000 time: 0 0.23 0.45 0.68 frequency in Hz Tuning = pitch of the fundamental (in this case 196 Hz) Timbre involves (a) pattern of overtones (Helmholtz) (b) temporal features 3 Some intervals “harmonious” and others “discordant.” Why? X X X X 1.06:1 2:1 X X X X 1.89:1 3:2 X X X X 1.414:1 4:3 4 Theory #1:(Pythagoras ) Humans naturally like the sound of intervals de- fined by small integer ratios. small ratios imply short period of repetition short = simple = sweet Theory #2:(Helmholtz ) Partials of a sound that are close in frequency cause beats that are perceived as “roughness” or dissonance. -

When the Leading Tone Doesn't Lead: Musical Qualia in Context
When the Leading Tone Doesn't Lead: Musical Qualia in Context Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Claire Arthur, B.Mus., M.A. Graduate Program in Music The Ohio State University 2016 Dissertation Committee: David Huron, Advisor David Clampitt Anna Gawboy c Copyright by Claire Arthur 2016 Abstract An empirical investigation is made of musical qualia in context. Specifically, scale-degree qualia are evaluated in relation to a local harmonic context, and rhythm qualia are evaluated in relation to a metrical context. After reviewing some of the philosophical background on qualia, and briefly reviewing some theories of musical qualia, three studies are presented. The first builds on Huron's (2006) theory of statistical or implicit learning and melodic probability as significant contributors to musical qualia. Prior statistical models of melodic expectation have focused on the distribution of pitches in melodies, or on their first-order likelihoods as predictors of melodic continuation. Since most Western music is non-monophonic, this first study investigates whether melodic probabilities are altered when the underlying harmonic accompaniment is taken into consideration. This project was carried out by building and analyzing a corpus of classical music containing harmonic analyses. Analysis of the data found that harmony was a significant predictor of scale-degree continuation. In addition, two experiments were carried out to test the perceptual effects of context on musical qualia. In the first experiment participants rated the perceived qualia of individual scale-degrees following various common four-chord progressions that each ended with a different harmony. -

HOW to FIND RELATIVE MINOR and MAJOR SCALES Relative
HOW TO FIND RELATIVE MINOR AND MAJOR SCALES Relative minor and major scales share all the same notes–each one just has a different tonic. The best example of this is the relative relationship between C-major and A-minor. These two scales have a relative relationship and therefore share all the same notes. C-major: C D E F G A B C A-minor: A B C D E F G A Finding the relative minor from a known major scale (using the 6th scale degree) scale degrees: 1 2 3 4 5 6 7 1 C-major: C D E F G A B C A-(natural) minor: A B C D E F G A A-minor starts on the 6th scale degree of C-major. This relationship holds true for ALL major and minor scale relative relationships. To find the relative minor scale from a given major scale, count up six scale degrees in the major scale–that is where the relative minor scale begins. This minor scale will be the natural minor mode. 1 2 3 4 5 6 C-D-E-F-G-A The relative minor scale can also be found by counting backwards (down) by three scale degrees in the major scale. C-major: C D E F G A B C ←←← count DOWN three scale degrees and arrive at A 1 2 3 C-B-A Finding the relative major from a known minor scale (using the 3rd scale degree) scale degrees: 1 2 3 4 5 6 7 1 A-(natural) minor: A B C D E F G A C-major: C D E F G A B C C-major starts on the 3rd scale of A-minor. -

The Unexpected Number Theory and Algebra of Musical Tuning Systems Or, Several Ways to Compute the Numbers 5,7,12,19,22,31,41,53, and 72
The Unexpected Number Theory and Algebra of Musical Tuning Systems or, Several Ways to Compute the Numbers 5,7,12,19,22,31,41,53, and 72 Matthew Hawthorn \Music is the pleasure the human soul experiences from counting without being aware that it is counting." -Gottfried Wilhelm von Leibniz (1646-1716) \All musicians are subconsciously mathematicians." -Thelonius Monk (1917-1982) 1 Physics In order to have music, we must have sound. In order to have sound, we must have something vibrating. Wherever there is something virbrating, there is the wave equation, be it in 1, 2, or more dimensions. The solutions to the wave equation for any given object (string, reed, metal bar, drumhead, vocal cords, etc.) with given boundary conditions can be expressed as a superposition of discrete partials, modes of vibration of which there are generally infinitely many, each with a characteristic frequency. The partials and their frequencies can be found as eigenvectors, resp. eigenvalues of the Laplace operator acting on the space of displacement functions on the object. Taken together, these frequen- cies comprise the spectrum of the object, and their relative intensities determine what in musical terms we call timbre. Something very nice occurs when our object is roughly one-dimensional (e.g. a string): the partial frequencies become harmonic. This is where, aptly, the better part of harmony traditionally takes place. For a spectrum to be harmonic means that it is comprised of a fundamental frequency, say f, and all whole number multiples of that frequency: f; 2f; 3f; 4f; : : : It is here also that number theory slips in the back door. -

The Major Scale Music Sounds the Way It Does Has to Do with the Group of Notes the Composer Decided to Use
music theory for musicians and normal people by toby w. rush one of the reasons that a particular piece of The Major Scale music sounds the way it does has to do with the group of notes the composer decided to use. 2 2 , 17 bach na e bachr a magdal ian jo t a ann bas m G for se n i ann ook oh eb inuett j M no œ#œ œ œ œ œ œ &43 œ œ œ œ œ œ œœœ œ œ œ œ œ œ œ œ œ œ œ œ œ œ ˙. take this melody, for example... let’s first remove all the duplicate notes, regardless of which octave they’re in. œ#œ œ &43 œ œ œ œ next, let’s put the notes in alphabetical order, œ #œ œ starting on the note œ #œ œ œ œ œ that the melody sounded œ œ œ œ like it was centering on. œ œ what we end up with there are actually many is the for “palette” different types of scales, this particular piece... each with a different pattern of whole steps and half steps. œ œ œ #œ œ œ œ œ a half step is the distance between like the board on which a painter holds two adjacent keys the bits of paint being used in the painting on the piano keyboard, being created. regardless of color. in music, this “palette” is called a scale. though we usually write scales from low to high, the order is actually unimportant; it’s the notes contained in the scale that help make a piece sound the way it does. -

11-Music Scales
Scales in Music Gary Hardegree Department of Philosophy University of Massachusetts Amherst, MA 01003 1. Introduction......................................................................................................................................1 2. The Fundamental Unit – The Octave...............................................................................................2 1. An Aside on Logarithmic Scales .........................................................................................5 2. Cents and Sensibility............................................................................................................6 3. The Pythagorean Construction of the Major Scale..........................................................................7 4. Ptolemaic Tuning...........................................................................................................................10 5. Mean-Tone Temperament (Tuning by Major Thirds) ...................................................................11 6. Problems with Perfect Tuning........................................................................................................12 1. An Aside on The Circle of Fifths and the Circle of Thirds................................................14 2. Back to the Problem of Tuning by Fifths...........................................................................14 3. Ptolemaic Tuning Makes Matters Even Worse! ................................................................15 4. Mean-Tone Temperament’s Wolves..................................................................................17