DOCSLIB.ORG

A LIGHTWEIGHT NOTATION for PLAYING PIANO for FUN by R.J.A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A LIGHTWEIGHT NOTATION for PLAYING PIANO for FUN by R.J.A A LIGHTWEIGHT NOTATION FOR PLAYING PIANO FOR FUN by R.J.A. Buhr 1. INTRODUCTION Music notation gets in the way of the joy of making music on the piano that can be had without first spending thousands of hours at the keyboard to develop piano “wizardry,” meaning a combination of keyboard skill and mastery of music notation. The message of this document is the joy can be had, without any loss of musical substance, with no more wizardry than is required to read and play single melody lines. The vehicle is a lightweight notation I call PKP (for Picturing Keyboard Patterns) for annotating the core flow of harmony in interval terms above the staff. I developed the notation as an adult beginner with no training in music theory after becoming frustrated with the way music notation obscures the keyboard simplicity of harmony. That the notation has substance in spite of this humble origin is indicated by the following opinion of PKP provided by a music theorist specializing in improvisational music (see supplementary pages): “The hook ... , at least in my opinion, is that it's possible to attain a deep understanding of chords (and their constituent intervals) without recourse to Western notation. This has direct consequences for physical patterning, fingerings, etc. Essentially, your method combines the utility of a play-by-ear approach with the depth of a mathematically-informed theory of music.” PKP follows from two observations that anyone can make. One is the piano keyboard supplies only 12 piano keys to play all the notes of an octave that music notation describes in many more than 12 ways by key signatures and accidentals (sharps, flats, naturals). This presents pianists with a 12-half- tone chromatic scale in which the intervals that provide what music is to the ears are directly visibly to the eyes as musical objects defined by size measured in half tones instead of by pairs of note symbols expressed in key-signature notation. The other observation is chord symbols describe chords without reference to context (melody line, other chords) in a way that obscures the often beautifully integrated flow of melody and harmony.1 A sufficient representation that captures this flow is a harmonic core formed of a sequence of two kinds of building blocks, which are keyboard intervals (measured in half tones) chosen to represent chords in context. Building blocks are intervals that split octaves in half in two ways. The first kind consists of fifths (7 half tones) and fourths (5 half tones) that split octaves into harmonious pitch halves. The second kind consists of tritones (6 half tones) that split octaves into dissonant keyboard halves midway in size between fifths and fourths. The closeness in size of these building blocks means that sequences of them establish smooth flow that cues what comes next. This works because chords described by chord symbols are formed either of single building blocks with a middle note (triad chords) or overlapped combinations of 2 or 3 building blocks (seventh or sixth chords). A melody line plus a harmonic core consisting of a sequence of primary building blocks captures the essence of the most sophisticated features of the harmony. It also identifies context in the form of tonic scales in play, enabling missing details to be filled in by eye and ear. The PKP notation for annotating this above the staff is easy to extract from music notation and is helpful for learning new pieces, all the way to guiding improvisations based on them. 1 The following ugly chord progression obscures the beautifully integrated flow of melody & harmony of a haunting minor blues with a simple, mainly-black-key melody line (see Chapter 3): E♭7♯9—B9(13)—EM9—A7♯11—D♭9sus—B9(13)—D♭7sus—E♭7—A♭m11— B7(13)—Fm7♭5—B♭7♯5♯9—C13♯11—F7(13)—B7—EM7—A7(13)—A♭7—B♭7—D♭7—E♭7♯9—B7—EM7♯11—A7♯11. www.pianotheoryman.com 2. CONCEPTS & NOTATION I was puzzled as a youth, when I picked up playing the trumpet in school bands, by the heavyweight notation required for music with tonic changes that could be effortlessly handled by ear by anyone when humming, whistling or singing a tune. I wondered why music could not be written down as simply as it is heard, but accepted that it could not as one of the mysteries of life and got on with the business of learning to read the notation as best I could. The puzzlement resurfaced when I took up the piano as an adult beginner. This time I decided not to ignore it. Music notation is here to stay and must be dealt with as it is by anyone aspiring to be a piano wizard but I wasn’t aspiring to that — I only wanted to play for fun — and I was not convinced that such heavyweight notation was necessary for the purpose. I was motivated to play harmonically sophisticated pieces from the “jazz and standards” repertoire that are available in numerous fake books. I had in mind pieces by the likes of, in no particular order, Bill Evans, Duke Ellington, Billy Strayhorn, Michel Legrand, Charles Mingus, George Gershwin, Thelonious Monk, John Coltrane and many more. Beyond specific pieces, I also wanted to learn how to play blues, which is often complex in music notation because its scales and chords tend to be strongly chromatic (an example is footnoted in the previous chapter). I once heard a jazz musician say in a radio interview that learning to play the blues before learning music notation had prepared him for anything music notation later threw at him. I wanted to focus practicing on pieces I loved instead of on developing general sight-reading and pianistic skills needed to become a piano wizard. I thought that a suitably lightweight notation to guide such practicing might be possible in terms of intervals instead of the notes of key-signature notation, and so it turned out to be. The concepts are very simple but be warned that they go strongly against conventional wisdom. They are simple if you shut music notation out of the mind until they are grasped. This is not to suggest discarding music notation. PKP is an aid to understanding it, not a replacement for it. No one is better qualified to shut music notation out of the mind than a skeptical adult beginner not yet versed in it. Skepticism followed from the visible mismatch between chord-progression-ugliness of the kind footnoted in the opening chapter and the simple beauty of the music it represents. Looking for a lightweight notation became an absorbing retirement hobby. A LIGHTWEIGHT NOTATION BASED ON INTERVALS Key signatures are the basis of written music, so a lightweight notation based on intervals must start with the scales of key signatures if it is to be helpful in understanding written music. The chromatic scale of a tonic octave on the piano provides the basis for this. Chromatic Scale Any tonic scale on the piano can be understood in terms of the intervals of the chromatic scale of the tonic octave represented by a line marked off in equal intervals representing half tones, as shown next. Every proper tonic scale is framed by the tonic notes an octave apart and the pitch center of the octave, a fifth above the bottom (a fourth below the top). pitch tonic chromatic scale center tonic @ $ @ <== tonic scale "frame" An unadorned divided line of the form shown above, displayed horizontally or vertically on the PKP 3/9/16 —!2— ©copyright R.J.A. Buhr www.pianotheoryman.com page will serve from now on as a representation of the chromatic scale of a designated tonic octave on the piano, understanding that the thicker markers identify the asymmetric divisions of the frame. Intervals have the same number of half tones whether they are understood in terms of this picture of the piano’s chromatic scale, or in terms of pairs of notes of music notation.2 The difference with music notation is not in the number of half tones but in their individual sizes in pitch terms. The half tones of music notation are nominally slightly different pitch sizes for overlapped octaves. Piano keys would need adjustable pitches to play the differences, and they don’t have them. One octave of the piano keyboard can be tuned to the musical perfection implied by music notation but this would make octaves overlapping it sound different. Instead, equal temperament tuning is used to make overlapping octaves sound the same, making them all nominally slightly out of tune. The book How Equal Temperament Tuning Ruined Harmony strongly expresses the opinion of its title, and the book Lies My Music Teacher Told Me explains that singers in choirs trained to sing the slightly different pitches by ear can find singing with the piano slightly uncomfortable. Opinions and comfort aside, the piano is the way it is and delivers intervals that are musically accurate in terms of sizes measured in half tones. This enables PKP to dispense with sharps and flats. Seasoned pianists tend to think they are needed as indicators of the musical functions of notes because they use them for that, but the fact is that the positions of notes relative to tonics are sufficient. Why not take advantage of this simplicity? The very thought goes strongly against musical tradition and conventional wisdom. I have been accused by piano wizards of being a musical know-nothing for even suggesting it. Read on and judge for yourself.
Load more

Recommended publications
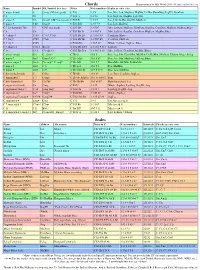
  • Chords and Scales 30/09/18 3:21 PM
    Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø
    [Show full text]
  • Naming a Chord Once You Know the Common Names of the Intervals, the Naming of Chords Is a Little Less Daunting
    Naming a Chord Once you know the common names of the intervals, the naming of chords is a little less daunting. Still, there are a few conventions and short-hand terms that many musicians use, that may be confusing at times. A few terms are used throughout the maze of chord names, and it is good to know what they refer to: Major / Minor – a “minor” note is one half step below the “major.” When naming intervals, all but the “perfect” intervals (1,4, 5, 8) are either major or minor. Generally if neither word is used, major is assumed, unless the situation is obvious. However, when used in naming extended chords, the word “minor” usually is reserved to indicate that the third of the triad is flatted. The word “major” is reserved to designate the major seventh interval as opposed to the minor or dominant seventh. It is assumed that the third is major, unless the word “minor” is said, right after the letter name of the chord. Similarly, in a seventh chord, the seventh interval is assumed to be a minor seventh (aka “dominant seventh), unless the word “major” comes right before the word “seventh.” Thus a common “C7” would mean a C major triad with a dominant seventh (CEGBb) While a “Cmaj7” (or CM7) would mean a C major triad with the major seventh interval added (CEGB), And a “Cmin7” (or Cm7) would mean a C minor triad with a dominant seventh interval added (CEbGBb) The dissonant “Cm(M7)” – “C minor major seventh” is fairly uncommon outside of modern jazz: it would mean a C minor triad with the major seventh interval added (CEbGB) Suspended – To suspend a note would mean to raise it up a half step.
    [Show full text]
  • MUSIC THEORY UNIT 5: TRIADS Intervallic Structure of Triads
    MUSIC THEORY UNIT 5: TRIADS Intervallic structure of Triads Another name of an interval is a “dyad” (two pitches). If two successive intervals (3 notes) happen simultaneously, we now have what is referred to as a chord or a “triad” (three pitches) Major and Minor Triads A Major triad consists of a M3 and a P5 interval from the root. A minor triad consists of a m3 and a P5 interval from the root. Diminished and Augmented Triads A diminished triad consists of a m3 and a dim 5th interval from the root. An augmented triad consists of a M3 and an Aug 5th interval from the root. The augmented triad has a major third interval and an augmented fifth interval from the root. An augmented triad differs from a major triad because the “5th” interval is a half-step higher than it is in the major triad. The diminished triad differs from minor triad because the “5th” interval is a half-step lower than it is in the minor triad. Recommended process: 1. Memorize your Perfect 5th intervals from most root pitches (ex. A-E, B-F#, C-G, D-A, etc…) 2. Know that a Major 3rd interval is two whole steps from a root pitch If you can identify a M3 and P5 from a root, you will be able to correctly spell your Major Triads. 3. If you need to know a minor triad, adjust the 3rd of the major triad down a half step to make it minor. 4. If you need to know an Augmented triad, adjust the 5th of the chord up a half step from the MAJOR triad.
    [Show full text]
  • Day 17 AP Music Handout, Scale Degress.Mus
    Scale Degrees, Chord Quality, & Roman Numeral Analysis There are a total of seven scale degrees in both major and minor scales. Each of these degrees has a name which you are required to memorize tonight. 1 2 3 4 5 6 7 1 & w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic A triad can be built upon each scale degree. w w w w & w w w w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic The quality and scale degree of the triads is shown by Roman numerals. Captial numerals are used to indicate major triads with lowercase numerals used to show minor triads. Diminished triads are lowercase with a "degree" ( °) symbol following and augmented triads are capital followed by a "plus" ( +) symbol. Roman numerals written for a major key look as follows: w w w w & w w w w w w w w CM: wI (M) iiw (m) wiii (m) IV (M) V (M) vi (m) vii° (dim) I (M) EVERY MAJOR KEY FOLLOWS THE PATTERN ABOVE FOR ITS ROMAN NUMERALS! Because the seventh scale degree in a natural minor scale is a whole step below tonic instead of a half step, the name is changed to subtonic, rather than leading tone. Leading tone ALWAYS indicates a half step below tonic. Notice the change in the qualities and therefore Roman numerals when in the natural minor scale.
    [Show full text]
  • Practical Music Theory – Book 1 by Pete Ford Table of Contents
    Practical Music Theory – Book 1 by Pete Ford Table of Contents Preface xi About This Book Series xii To the Instructor xii Acknowledgements xii Part One Chapter 1: Notation 1 Clefs 1 The Grand Staff 2 Notes 2 Rests 3 Note Names 4 Rhythm 5 Simple Time 6 Dotted Notes in Simple Time 7 Compound Time 8 Subdivision in Compound Time 10 The Phrase Marking, Slur and the Tie 12 The Tie in Simple Time 12 The Tie in Compound Time 13 Repeat Signs, da Capo, and More 14 Assignment 1-1: Name the Notes 19 Assignment 1-2: Simple Time 21 Assignment 1-3: Compound Time 23 Chapter 2: Key Signatures 25 Writing Accidental Signs 25 The Cycle of Fourths 26 Key Signatures with Flats 27 Key Signatures with Sharps 28 Enharmonic Keys 30 Assignment 2-1: Name the Key Signature 33 Assignment 2-2: Key Signatures 35 Table of Contents Chapter 3: Building Scales 37 Writing the Major Scale 38 Introduction to Solfege 39 The Relative Minor Scale 40 The Cycle with Minor Keys Added 41 Writing the Natural Minor Scale 41 Solfege in Minor Keys 42 The Harmonic Minor Scale 44 The Melodic Minor Scale 46 Assignment 3-1: Write the Scales #1 49 Assignment 3-2: Write the Scales #2 51 Chapter 4: Intervals 53 Primary Intervals of the Major Scale 53 Writing Ascending Intervals 55 Writing Descending Intervals 57 Playing Intervals on the Piano 59 Hearing and Singing Intervals 59 Secondary Intervals 60 Writing Descending Secondary Intervals 62 Assignment 4-1: Write the Intervals 65 Assignment 4-2: Secondary Intervals 67 Part Two Chapter 5: Building Chords (SATB) 71 Triads of the Major Scale
    [Show full text]
  • The Sonata, Its Form and Meaning As Exemplified in the Piano Sonatas by Mozart
    THE SONATA, ITS FORM AND MEANING AS EXEMPLIFIED IN THE PIANO SONATAS BY MOZART. MOZART. Portrait drawn by Dora Stock when Mozart visited Dresden in 1789. Original now in the possession of the Bibliothek Peters. THE SONATA ITS FORM AND MEANING AS EXEMPLIFIED IN THE PIANO SONATAS BY MOZART A DESCRIPTIVE ANALYSIS BY F. HELENA MARKS WITH MCSICAL EXAMPLES LONDON WILLIAM REEVES, 83 CHARING CROSS ROAD, W.C.2. Publisher of Works on Music. BROUDE BROS. Music NEW YORK Presented to the LIBRARY of the UNIVERSITY OF TORONTO from the Library of DR. ARTHUR PLETTNER AND ISA MCILWRAITH PLETTNER Crescent, London, S.W.16. Printed by The New Temple Press, Norbury PREFACE. undertaking the present work, the writer's intention originally was IN to offer to the student of musical form an analysis of the whole of Mozart's Pianoforte Sonatas, and to deal with the subject on lines some- what similar to those followed by Dr. Harding in his volume on Beet- hoven. A very little thought, however, convinced her that, though students would doubtless welcome such a book of reference, still, were the scope of the treatise thus limited, its sphere of usefulness would be somewhat circumscribed. " Mozart was gifted with an extraordinary and hitherto unsurpassed instinct for formal perfection, and his highest achievements lie not more in the tunes which have so captivated the world, than in the perfect sym- metry of his best works In his time these formal outlines were fresh enough to bear a great deal of use without losing their sweetness; arid Mozart used them with remarkable regularity."* The author quotes the above as an explanation of certain broad similarities of treatment which are to be found throughout Mozart's sonatas.
    [Show full text]
  • The Misunderstood Eleventh Amendment
    UNIVERSITY of PENNSYLVANIA LAW REVIEW Founded !"#$ Formerly AMERICAN LAW REGISTER © !"!# University of Pennsylvania Law Review VOL. !"# FEBRUARY $%$! NO. & ARTICLE THE MISUNDERSTOOD ELEVENTH AMENDMENT WILLIAM BAUDE† & STEPHEN E. SACHS†† The Eleventh Amendment might be the most misunderstood amendment to the Constitution. Both its friends and enemies have treated the Amendment’s written † Professor of Law, University of Chicago Law School. †† Colin W. Brown Professor of Law, Duke University School of Law. We are grateful for comments and suggestions from Sam Bray, Tom Colby, Scott Dodson, Jonathan Gienapp, Tara Grove, Julian Davis Mortenson, Caleb Nelson, Jim Pfander, Richard Re, Amanda Schwoerke, Eric Segall, Jonathan Urick, Ingrid Wuerth, and from participants in the Fall Speaker Series of the Georgetown Center for the Constitution, the Hugh & Hazel Darling Foundation Originalism Works-in-Progress Conference at the University of San Diego Law School, and Advanced Topics in Federal Courts at the University of Virginia School of Law. Thanks as well to Brendan Anderson, Kurtis Michael, and Scotty Schenck for research assistance, and to the SNR Denton Fund and Alumni Faculty Fund at Chicago for research support. (!"#) !"# University of Pennsylvania Law Review [Vol. "!$: !#$ text, and the unwritten doctrines of state sovereign immunity, as one and the same— reading broad principles into its precise words, or treating the written Amendment as merely illustrative of unwritten doctrines. The result is a bewildering forest of case law, which takes neither the words nor the doctrines seriously. The truth is simpler: the Eleventh Amendment means what it says. It strips the federal government of judicial power over suits against states, in law or equity, brought by diverse plaintiffs.
    [Show full text]
  • The Devil's Interval by Jerry Tachoir
    Sound Enhanced Hear the music example in the Members Only section of the PAS Web site at www.pas.org The Devil’s Interval BY JERRY TACHOIR he natural progression from consonance to dissonance and ii7 chords. In other words, Dm7 to G7 can now be A-flat m7 to resolution helps make music interesting and satisfying. G7, and both can resolve to either a C or a G-flat. Using the TMusic would be extremely bland without the use of disso- other dominant chord, D-flat (with the basic ii7 to V7 of A-flat nance. Imagine a world of parallel thirds and sixths and no dis- m7 to D-flat 7), we can substitute the other relative ii7 chord, sonance/resolution. creating the progression Dm7 to D-flat 7 which, again, can re- The prime interval requiring resolution is the tritone—an solve to either a C or a G-flat. augmented 4th or diminished 5th. Known in the early church Here are all the possibilities (Note: enharmonic spellings as the “Devil’s interval,” tritones were actually prohibited in of- were used to simplify the spelling of some chords—e.g., B in- ficial church music. Imagine Bach’s struggle to take music stead of C-flat): through its normal progression of tonic, subdominant, domi- nant, and back to tonic without the use of this interval. Dm7 G7 C Dm7 G7 Gb The tritone is the characteristic interval of all dominant bw chords, created by the “guide tones,” or the 3rd and 7th. The 4 ˙ ˙ w ˙ ˙ tritone interval can be resolved in two types of contrary motion: &4˙ ˙ w ˙ ˙ bbw one in which both notes move in by half steps, and one in which ˙ ˙ w ˙ ˙ b w both notes move out by half steps.
    [Show full text]
  • Major and Minor Scales Half and Whole Steps
    Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale.
    [Show full text]
  • Ninth, Eleventh and Thirteenth Chords Ninth, Eleventh and Thirteen Chords Sometimes Referred to As Chords with 'Extensions', I.E
    Ninth, Eleventh and Thirteenth chords Ninth, Eleventh and Thirteen chords sometimes referred to as chords with 'extensions', i.e. extending the seventh chord to include tones that are stacking the interval of a third above the basic chord tones. These chords with upper extensions occur mostly on the V chord. The ninth chord is sometimes viewed as superimposing the vii7 chord on top of the V7 chord. The combination of the two chord creates a ninth chord. In major keys the ninth of the dominant ninth chord is a whole step above the root (plus octaves) w w w w w & c w w w C major: V7 vii7 V9 G7 Bm7b5 G9 ? c ∑ ∑ ∑ In the minor keys the ninth of the dominant ninth chord is a half step above the root (plus octaves). In chord symbols it is referred to as a b9, i.e. E7b9. The 'flat' terminology is use to indicate that the ninth is lowered compared to the major key version of the dominant ninth chord. Note that in many keys, the ninth is not literally a flatted note but might be a natural. 4 w w w & #w #w #w A minor: V7 vii7 V9 E7 G#dim7 E7b9 ? ∑ ∑ ∑ The dominant ninth usually resolves to I and the ninth often resolves down in parallel motion with the seventh of the chord. 7 ˙ ˙ ˙ ˙ & ˙ ˙ #˙ ˙ C major: V9 I A minor: V9 i G9 C E7b9 Am ˙ ˙ ˙ ˙ ˙ ? ˙ ˙ The dominant ninth chord is often used in a II-V-I chord progression where the II chord˙ and the I chord are both seventh chords and the V chord is a incomplete ninth with the fifth omitted.
    [Show full text]
  • When the Leading Tone Doesn't Lead: Musical Qualia in Context
    When the Leading Tone Doesn't Lead: Musical Qualia in Context Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Claire Arthur, B.Mus., M.A. Graduate Program in Music The Ohio State University 2016 Dissertation Committee: David Huron, Advisor David Clampitt Anna Gawboy c Copyright by Claire Arthur 2016 Abstract An empirical investigation is made of musical qualia in context. Specifically, scale-degree qualia are evaluated in relation to a local harmonic context, and rhythm qualia are evaluated in relation to a metrical context. After reviewing some of the philosophical background on qualia, and briefly reviewing some theories of musical qualia, three studies are presented. The first builds on Huron's (2006) theory of statistical or implicit learning and melodic probability as significant contributors to musical qualia. Prior statistical models of melodic expectation have focused on the distribution of pitches in melodies, or on their first-order likelihoods as predictors of melodic continuation. Since most Western music is non-monophonic, this first study investigates whether melodic probabilities are altered when the underlying harmonic accompaniment is taken into consideration. This project was carried out by building and analyzing a corpus of classical music containing harmonic analyses. Analysis of the data found that harmony was a significant predictor of scale-degree continuation. In addition, two experiments were carried out to test the perceptual effects of context on musical qualia. In the first experiment participants rated the perceived qualia of individual scale-degrees following various common four-chord progressions that each ended with a different harmony.
    [Show full text]
  • Boris's Bells, by Way of Schubert and Others
    Boris's Bells, By Way of Schubert and Others Mark DeVoto We define "bell chords" as different dominant-seventh chords whose roots are separated by multiples of interval 3, the minor third. The sobriquet derives from the most famous such pair of harmonies, the alternating D7 and AI? that constitute the entire harmonic substance of the first thirty-eight measures of scene 2 of the Prologue in Musorgsky's opera Boris Godunov (1874) (example O. Example 1: Paradigm of the Boris Godunov bell succession: AJ,7-D7. A~7 D7 '~~&gl n'IO D>: y 7 G: y7 The Boris bell chords are an early milestone in the history of nonfunctional harmony; yet the two harmonies, considered individually, are ofcourse abso­ lutely functional in classical contexts. This essay traces some ofthe historical antecedents of the bell chords as well as their developing descendants. Dominant Harmony The dominant-seventh chord is rightly recognized as the most unambiguous of the essential tonal resources in classical harmonic progression, and the V7-1 progression is the strongest means of moving harmony forward in immediate musical time. To put it another way, the expectation of tonic harmony to follow a dominant-seventh sonority is a principal component of forehearing; we assume, in our ordinary and long-tested experience oftonal music, that the tonic function will follow the dominant-seventh function and be fortified by it. So familiar is this everyday phenomenon that it hardly needs to be stated; we need mention it here only to assert the contrary case, namely, that the dominant-seventh function followed by something else introduces the element of the unexpected.
    [Show full text]