DOCSLIB.ORG

When the Leading Tone Doesn't Lead: Musical Qualia in Context

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
When the Leading Tone Doesn't Lead: Musical Qualia in Context When the Leading Tone Doesn't Lead: Musical Qualia in Context Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Claire Arthur, B.Mus., M.A. Graduate Program in Music The Ohio State University 2016 Dissertation Committee: David Huron, Advisor David Clampitt Anna Gawboy c Copyright by Claire Arthur 2016 Abstract An empirical investigation is made of musical qualia in context. Specifically, scale-degree qualia are evaluated in relation to a local harmonic context, and rhythm qualia are evaluated in relation to a metrical context. After reviewing some of the philosophical background on qualia, and briefly reviewing some theories of musical qualia, three studies are presented. The first builds on Huron's (2006) theory of statistical or implicit learning and melodic probability as significant contributors to musical qualia. Prior statistical models of melodic expectation have focused on the distribution of pitches in melodies, or on their first-order likelihoods as predictors of melodic continuation. Since most Western music is non-monophonic, this first study investigates whether melodic probabilities are altered when the underlying harmonic accompaniment is taken into consideration. This project was carried out by building and analyzing a corpus of classical music containing harmonic analyses. Analysis of the data found that harmony was a significant predictor of scale-degree continuation. In addition, two experiments were carried out to test the perceptual effects of context on musical qualia. In the first experiment participants rated the perceived qualia of individual scale-degrees following various common four-chord progressions that each ended with a different harmony. While scale-degrees were still shown to elicit relatively stable qualia, there was a significant effect for the role of the local chord context. Importantly, this experiment was carried out using participants both with ii and without music-theoretic training, supporting the notion that the identification of scale-degrees was not responsible for the evoked qualia. This experiment also partially replicated a component of Krumhansl & Kessler's (1982) study examining the \goodness of fit” of scale-degrees within a key. However, the authors' claim that scale-degrees 1, 3, and 5 were best “fitting” due to the tonal stability of the tonic triad could not be fully supported here. In fact, the results from the present study found that the \goodness of fit” effect could perhaps be better explained by other factors. In the second experiment participants rated the perceived qualia of either com- posed inter-onset patterns or recorded song clips presented in different metrical con- texts. Both inter-onset interval pattern and meter were shown to be significant in- fluences on judgments of qualia. In addition, syncopation was found to be a strong predictor for certain components of qualia. The overall results from these studies show that musical context is an important contributor to musical qualia, and therefore, while isolated musical events may still be capable of creating relatively \stable" qualia, in real musical contexts these may change dramatically. iii Acknowledgments I would first and foremost like to thank my advisor, David Huron, for his con- tinuous guidance and support, and for his infectious curiosity and excitement for all things musical. I would also like to thank my fellow CSML colleagues, both past and present, for their feedback, advice, and camaraderie. In addition, many thanks are due to the other members of my committee, Anna Gawboy and David Clampitt, for their insights and encouragement throughout my time at Ohio State. I would also like to acknowledge the support of the Social Sciences Humanities Research Council of Canada, whose funding made possible my final year of study. Finally, I especially need to thank my \better half", Nat Condit-Schultz, for all of his help with statis- tics and programming, for his unfailing optimism, and above all, for inspiring me to become a better scholar and musician. iv Vita 2015{2016 . Graduate Research Assistant, Ohio State University School of Music 2012-2014 . Graduate Teaching Associate, Ohio State University School of Music 2008{2012 . Private Piano and Music Theory In- structor 2008 . .M.A., Music Theory, University of British Columbia 2004 . .B.Mus., Music Theory and History, University of Toronto Publications Research Publications Arthur, C., & Huron, D. (2016). The direct octaves rule: Testing a scene analysis interpretation. Musicae Scientiae. Advance online publication. doi: 10.1177/1029864915623093 Devaney, J., Arthur, C., Condit-Schultz, N., & Nisula, K. (2015). Theme and Vari- ations Encodings with Roman Numerals (TAVERN): A new data set for symbolic music analysis. In M. Muller & F. Wiering (Eds.), Proceedings of the International Society of Music Information Retrieval (ISMIR) Conference. Malaga, Spain: 728{ 734. Arthur, C. (2014). Does harmony affect scale-degree qualia?: A corpus study in- vestigating the relation of scale-degree and harmonic support. In M.K. Song (Ed.), Proceedings of the 13th International Conference for Music Perception and Cognition. Seoul, Korea: Yonsei University, 194{196. v Fields of Study Major Field: Music Area of Specialization: Music Theory vi Table of Contents Page Abstract . ii Acknowledgments . iv Vita.........................................v List of Tables . .x List of Figures . xi 1. Introduction . .1 2. On the Philosophy and Science of Musical Qualia . .4 2.1 What Are Qualia? . .4 2.2 The Problem Music Raises for the Study of Qualia (and Vice-Versa)6 2.3 Conceptual Knowledge and Qualia . .9 2.4 Qualia as Synthesis of Sensory and Cognitive Processing . 12 2.5 Introspection, Observation, and Converging Evidence . 13 2.6 Why Study Musical Qualia? . 14 2.7 Theories of Musical Qualia . 16 2.7.1 Scale-degree Qualia and Implicit Learning . 17 2.7.2 Rhythm Qualia . 21 2.8 Chapter Summary . 23 3. A Corpus Study . 26 3.1 The Corpus Analysis . 29 3.1.1 Overview . 29 3.1.2 Sampling . 30 vii 3.1.3 Methodology . 33 3.2 Evaluating the Models . 41 3.2.1 Global Hypothesis Test . 41 3.3 Descriptive Statistics . 44 3.3.1 Mode Classification . 44 3.3.2 Zeroth-order Probabilities . 46 3.3.3 First-order Probabilities . 49 3.3.4 Change in Melodic Probabilities when Harmony is Considered 52 3.4 Conclusions . 58 3.5 Discussion . 61 4. A Perceptual Study of Scale-degree in Context . 63 4.1 Introduction . 63 4.2 Method . 66 4.2.1 Participants . 69 4.2.2 Stimuli . 70 4.2.3 Procedure . 72 4.3 Results . 75 4.4 Discussion . 93 5. Rhythm Qualia . 96 5.1 Introduction . 96 5.1.1 Background . 100 5.2 A Perceptual Study: Rhythm in Context . 101 5.2.1 Introduction . 101 5.2.2 Method . 107 5.2.3 Results and Discussion . 110 5.2.4 Post-hoc Exploration of Rhythm Qualia . 120 5.3 Chapter Summary . 128 6. General Summary . 131 6.1 Recapitulation . 131 6.2 Discussion . 133 6.3 Implications for Music Pedagogy . 135 6.4 Areas for Future Research on Musical Qualia . 139 Works Cited . 141 viii Appendices 150 A. The Corpus Data . 150 ix List of Tables Table Page 3.1 Illustration of Encoding Key Changes . 38 3.2 Melody and Harmony Encodings at Key Changes . 40 4.1 Result Statistics by Dependent Variable . 76 4.2 Tally of \Opt-outs" by Dependent Variable . 77 4.3 Correlations with the K&K Profile . 89 5.1 Similarity Measures Between Dependent Variables . 114 5.2 Syncopation Scores for Rhythm Stimuli . 123 x List of Figures Figure Page 2.1 Example of Identical Acoustic Information Generating Unique Qualia 17 2.2 Flow Chart of Diatonic Scale-degree Probabilities from Huron (2006) 18 3.1 Zeroth-order Distribution of Scale-degrees in the Corpus . 47 3.2 Zeroth-order Distribution of Harmonies in the Corpus . 48 3.3 First-order Probabilities for Scale-degrees . 50 3.4 Predicted and Observed Probabilities for 1^ in Tonic Context . 53 3.5 Effect of Harmony on Scale-degree Probability (continued on next page) 55 4.1 Image of Digital Interface Used in Experiment . 73 4.2 Scale-degree Qualia Ratings (continued on next page) . 80 4.3 Consistency Between and Across Participants . 84 4.4 Intra-Subject Correlations . 86 4.5 Key Profiles from Krumhansl & Kessler (1982) . 87 4.6 Present Data Compared to Krumhansl & Kessler's (1982) Key Profiles 88 5.1 Three Identical Onset Patterns in Different Metrical Contexts . 99 5.2 Rhythm Stimuli (Composed) . 105 xi 5.3 Rhythm Stimuli (Borrowed) . 107 5.4 List of Rhythmic Descriptor Terms . 109 5.5 Rhythm Qualia Ratings - Composed Rhythms (continued on next page)111 5.6 Rhythm Qualia Ratings - Song Clips . 117 5.7 Amount of Syncopation and \Grooviness" . 124 5.8 Additional Examples of Syncopation Predicting Qualia . 125 xii Chapter 1: Introduction This dissertation examines whether certain fundamental components of musical structure, such as scale-degree and rhythm, can generate unique, qualitative musical experiences, or \qualia," and in particular whether the musical context | in this case harmony and meter, respectively | can affect those experiences. Chapter 2 introduces the topic of qualia, briefly mentions its philosophical origins, and discusses its role in music. In particular, the concepts of scale-degree and rhythm pose a challenge to many traditional accounts of what constitutes \qualia" on account of their being referential. In addition, many philosophers who claim qualia to be ineffable pose a challenge to empirical researchers wishing to study musical qualia. This chapter also reviews the literature on music and qualia, and summarizes theories about the generation of musical qualia, giving special attention to the role of implicit learning. It then proposes an operational definition of qualia, similar to those used by Zentner (2012) and Dowling (2010), that supports a perspective conducive to the evaluation of qualia as an object for scientific study.
Load more

Recommended publications
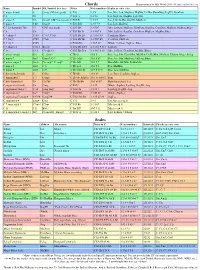
  • Chords and Scales 30/09/18 3:21 PM
    Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø
    [Show full text]
  • Expectancy and Musical Emotion Effects of Pitch and Timing
    Manuscript Expectancy and musical emotion Effects of pitch and timing expectancy on musical emotion Sauvé, S. A.1, Sayed, A.1, Dean, R. T.2, Pearce, M. T.1 1Queen Mary, University of London 2Western Sydney University Author Note Correspondence can be addressed to Sarah Sauvé at [email protected] School of Electronic Engineering and Computer Science Queen Mary University of London, Mile End Road London E1 4NS United Kingdom +447733661107 Biographies S Sauve: Originally a pianist, Sarah is now a PhD candidate in the Electronic Engineering and Computer Science department at Queen Mary University of London studying expectancy and stream segregation, supported by a college studentship. EXPECTANCY AND MUSICAL EMOTION 2 A Sayed: Aminah completed her MSc in Computer Science at Queen Mary University of London, specializing in multimedia. R.T. Dean: Roger is a composer/improviser and researcher at the MARCS Institute for Brain, Behaviour and Development. His research focuses on music cognition and music computation, both analytic and generative. M.T. Pearce: Marcus is Senior Lecturer at Queen Mary University of London, director of the Music Cognition and EEG Labs and co-director of the Centre for Mind in Society. His research interests cover computational, psychological and neuroscientific aspects of music cognition, with a particular focus on dynamic, predictive processing of melodic, rhythmic and harmonic structure, and its impact on emotional and aesthetic experience. He is the author of the IDyOM model of auditory expectation based on statistical learning and probabilistic prediction. EXPECTANCY AND MUSICAL EMOTION 3 Abstract Pitch and timing information work hand in hand to create a coherent piece of music; but what happens when this information goes against the norm? Relationships between musical expectancy and emotional responses were investigated in a study conducted with 40 participants: 20 musicians and 20 non-musicians.
    [Show full text]
  • The Form of the Preludes to Bach's Unaccompanied Cello Suites
    University of Massachusetts Amherst ScholarWorks@UMass Amherst Masters Theses 1911 - February 2014 2011 The orF m of the Preludes to Bach's Unaccompanied Cello Suites Daniel E. Prindle University of Massachusetts Amherst Follow this and additional works at: https://scholarworks.umass.edu/theses Part of the Composition Commons, Musicology Commons, Music Practice Commons, and the Music Theory Commons Prindle, Daniel E., "The orF m of the Preludes to Bach's Unaccompanied Cello Suites" (2011). Masters Theses 1911 - February 2014. 636. Retrieved from https://scholarworks.umass.edu/theses/636 This thesis is brought to you for free and open access by ScholarWorks@UMass Amherst. It has been accepted for inclusion in Masters Theses 1911 - February 2014 by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. THE FORM OF THE PRELUDES TO BACH’S UNACCOMPANIED CELLO SUITES A Thesis Presented by DANIEL E. PRINDLE Submitted to the Graduate School of the University of Massachusetts Amherst in partial fulfillment of the requirements for the degree of MASTER OF MUSIC May 2011 Master of Music in Music Theory © Copyright by Daniel E. Prindle 2011 All Rights Reserved ii THE FORM OF THE PRELUDES TO BACH’S UNACCOMPANIED CELLO SUITES A Thesis Presented by DANIEL E. PRINDLE Approved as to style and content by: _____________________________________ Gary Karpinski, Chair _____________________________________ Miriam Whaples, Member _____________________________________ Brent Auerbach, Member ___________________________________ Jeffrey Cox, Department Head Department of Music and Dance iii DEDICATION To Michelle and Rhys. iv ACKNOWLEDGEMENTS First and foremost, I would like to acknowledge the generous sacrifice made by my family.
    [Show full text]
  • A Group-Theoretical Classification of Three-Tone and Four-Tone Harmonic Chords3
    A GROUP-THEORETICAL CLASSIFICATION OF THREE-TONE AND FOUR-TONE HARMONIC CHORDS JASON K.C. POLAK Abstract. We classify three-tone and four-tone chords based on subgroups of the symmetric group acting on chords contained within a twelve-tone scale. The actions are inversion, major- minor duality, and augmented-diminished duality. These actions correspond to elements of symmetric groups, and also correspond directly to intuitive concepts in the harmony theory of music. We produce a graph of how these actions relate different seventh chords that suggests a concept of distance in the theory of harmony. Contents 1. Introduction 1 Acknowledgements 2 2. Three-tone harmonic chords 2 3. Four-tone harmonic chords 4 4. The chord graph 6 References 8 References 8 1. Introduction Early on in music theory we learn of the harmonic triads: major, minor, augmented, and diminished. Later on we find out about four-note chords such as seventh chords. We wish to describe a classification of these types of chords using the action of the finite symmetric groups. We represent notes by a number in the set Z/12 = {0, 1, 2,..., 10, 11}. Under this scheme, for example, 0 represents C, 1 represents C♯, 2 represents D, and so on. We consider only pitch classes modulo the octave. arXiv:2007.03134v1 [math.GR] 6 Jul 2020 We describe the sounding of simultaneous notes by an ordered increasing list of integers in Z/12 surrounded by parentheses. For example, a major second interval M2 would be repre- sented by (0, 2), and a major chord would be represented by (0, 4, 7).
    [Show full text]
  • Many of Us Are Familiar with Popular Major Chord Progressions Like I–IV–V–I
    Many of us are familiar with popular major chord progressions like I–IV–V–I. Now it’s time to delve into the exciting world of minor chords. Minor scales give flavor and emotion to a song, adding a level of musical depth that can make a mediocre song moving and distinct from others. Because so many of our favorite songs are in major keys, those that are in minor keys1 can stand out, and some musical styles like rock or ​ ​ jazz thrive on complex minor scales and harmonic wizardry. Minor chord progressions generally contain richer harmonic possibilities than the typical major progressions. Minor key songs frequently modulate to major and back to minor. Sometimes the same chord can appear as major and minor in the very same song! But this heady harmonic mix is nothing to be afraid of. By the end of this article, you’ll not only understand how minor chords are made, but you’ll know some common minor chord progressions, how to write them, and how to use them in your own music. With enough listening practice, you’ll be able to recognize minor chord progressions in songs almost instantly! Table of Contents: 1. A Tale of Two Tonalities 2. Major or Minor? 3. Chords in Minor Scales 4. The Top 3 Chords in Minor Progressions 5. Exercises in Minor 6. Writing Your Own Minor Chord Progressions 7. Your Minor Journey 1 https://www.musical-u.com/learn/the-ultimate-guide-to-minor-keys A Tale of Two Tonalities Western music is dominated by two tonalities: major and minor.
    [Show full text]
  • A New Illusion in the Perception of Relative Pitch Intervals
    A new illusion in the perception of relative pitch intervals by Maartje Koning A thesis submitted to the Faculty of Humanities of the University of Amsterdam in partial fulfilment of the requirements for the degree of Master of Arts Department of Musicology 2015 Dr. M. Sadakata University of Amsterdam Dr. J.A. Burgoyne University of Amsterdam 2 Abstract This study is about the perception of relative pitch intervals. An earlier study of Sadakata & Ohgushi ‘Comparative judgments pitch intervals and an illusion’ (2000) showed that when when people listened to two tone intervals, their perception of relative pitch distance between the two tones depended on the direction and size of the intervals. In this follow-up study the participants had to listen to two tone intervals and indicate whether the size of the second interval was smaller, the same or larger than the first. The conditions were the same as in the study of Sadakata & Ohgushi. These four different conditions were illustrating the relationship between those two intervals. There were ascending and descending intervals and the starting tone of the second interval differed with respect to the starting tone of the first interval. The study made use of small and large intervals and hypothesized that the starting tone of the second interval with respect to the starting tone of the first interval had an effect on the melodic expectancy of the listener and because of that they over- or underestimate the size of the second tone interval. Furthermore, it was predicted that this tendency would be stronger for larger tone intervals compared to smaller tone intervals and that there would be no difference found between musicians and non-musicians.
    [Show full text]
  • Day 17 AP Music Handout, Scale Degress.Mus
    Scale Degrees, Chord Quality, & Roman Numeral Analysis There are a total of seven scale degrees in both major and minor scales. Each of these degrees has a name which you are required to memorize tonight. 1 2 3 4 5 6 7 1 & w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic A triad can be built upon each scale degree. w w w w & w w w w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic The quality and scale degree of the triads is shown by Roman numerals. Captial numerals are used to indicate major triads with lowercase numerals used to show minor triads. Diminished triads are lowercase with a "degree" ( °) symbol following and augmented triads are capital followed by a "plus" ( +) symbol. Roman numerals written for a major key look as follows: w w w w & w w w w w w w w CM: wI (M) iiw (m) wiii (m) IV (M) V (M) vi (m) vii° (dim) I (M) EVERY MAJOR KEY FOLLOWS THE PATTERN ABOVE FOR ITS ROMAN NUMERALS! Because the seventh scale degree in a natural minor scale is a whole step below tonic instead of a half step, the name is changed to subtonic, rather than leading tone. Leading tone ALWAYS indicates a half step below tonic. Notice the change in the qualities and therefore Roman numerals when in the natural minor scale.
    [Show full text]
  • AP Music Theory Course Description Audio Files ”
    MusIc Theory Course Description e ffective Fall 2 0 1 2 AP Course Descriptions are updated regularly. Please visit AP Central® (apcentral.collegeboard.org) to determine whether a more recent Course Description PDF is available. The College Board The College Board is a mission-driven not-for-profit organization that connects students to college success and opportunity. Founded in 1900, the College Board was created to expand access to higher education. Today, the membership association is made up of more than 5,900 of the world’s leading educational institutions and is dedicated to promoting excellence and equity in education. Each year, the College Board helps more than seven million students prepare for a successful transition to college through programs and services in college readiness and college success — including the SAT® and the Advanced Placement Program®. The organization also serves the education community through research and advocacy on behalf of students, educators, and schools. For further information, visit www.collegeboard.org. AP Equity and Access Policy The College Board strongly encourages educators to make equitable access a guiding principle for their AP programs by giving all willing and academically prepared students the opportunity to participate in AP. We encourage the elimination of barriers that restrict access to AP for students from ethnic, racial, and socioeconomic groups that have been traditionally underserved. Schools should make every effort to ensure their AP classes reflect the diversity of their student population. The College Board also believes that all students should have access to academically challenging course work before they enroll in AP classes, which can prepare them for AP success.
    [Show full text]
  • Discover Seventh Chords
    Seventh Chords Stack of Thirds - Begin with a major or natural minor scale (use raised leading tone for chords based on ^5 and ^7) - Build a four note stack of thirds on each note within the given key - Identify the characteristic intervals of each of the seventh chords w w w w w w w w % w w w w w w w Mw/M7 mw/m7 m/m7 M/M7 M/m7 m/m7 d/m7 w w w w w w % w w w w #w w #w mw/m7 d/wm7 Mw/M7 m/m7 M/m7 M/M7 d/d7 Seventh Chord Quality - Five common seventh chord types in diatonic music: * Major: Major Triad - Major 7th (M3 - m3 - M3) * Dominant: Major Triad - minor 7th (M3 - m3 - m3) * Minor: minor triad - minor 7th (m3 - M3 - m3) * Half-Diminished: diminished triad - minor 3rd (m3 - m3 - M3) * Diminished: diminished triad - diminished 7th (m3 - m3 - m3) - In the Major Scale (all major scales!) * Major 7th on scale degrees 1 & 4 * Minor 7th on scale degrees 2, 3, 6 * Dominant 7th on scale degree 5 * Half-Diminished 7th on scale degree 7 - In the Minor Scale (all minor scales!) with a raised leading tone for chords on ^5 and ^7 * Major 7th on scale degrees 3 & 6 * Minor 7th on scale degrees 1 & 4 * Dominant 7th on scale degree 5 * Half-Diminished 7th on scale degree 2 * Diminished 7th on scale degree 7 Using Roman Numerals for Triads - Roman Numeral labels allow us to identify any seventh chord within a given key.
    [Show full text]
  • Chord Progressions
    Chord Progressions Part I 2 Chord Progressions The Best Free Chord Progression Lessons on the Web "The recipe for music is part melody, lyric, rhythm, and harmony (chord progressions). The term chord progression refers to a succession of tones or chords played in a particular order for a specified duration that harmonizes with the melody. Except for styles such as rap and free jazz, chord progressions are an essential building block of contemporary western music establishing the basic framework of a song. If you take a look at a large number of popular songs, you will find that certain combinations of chords are used repeatedly because the individual chords just simply sound good together. I call these popular chord progressions the money chords. These money chord patterns vary in length from one- or two-chord progressions to sequences lasting for the whole song such as the twelve-bar blues and thirty-two bar rhythm changes." (Excerpt from Chord Progressions For Songwriters © 2003 by Richard J. Scott) Every guitarist should have a working knowledge of how these chord progressions are created and used in popular music. Click below for the best in free chord progressions lessons available on the web. Ascending Augmented (I-I+-I6-I7) - - 4 Ascending Bass Lines - - 5 Basic Progressions (I-IV) - - 10 Basie Blues Changes - - 8 Blues Progressions (I-IV-I-V-I) - - 15 Blues With A Bridge - - 36 Bridge Progressions - - 37 Cadences - - 50 Canons - - 44 Circle Progressions -- 53 Classic Rock Progressions (I-bVII-IV) -- 74 Coltrane Changes -- 67 Combination
    [Show full text]
  • Surviving Set Theory: a Pedagogical Game and Cooperative Learning Approach to Undergraduate Post-Tonal Music Theory
    Surviving Set Theory: A Pedagogical Game and Cooperative Learning Approach to Undergraduate Post-Tonal Music Theory DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Angela N. Ripley, M.M. Graduate Program in Music The Ohio State University 2015 Dissertation Committee: David Clampitt, Advisor Anna Gawboy Johanna Devaney Copyright by Angela N. Ripley 2015 Abstract Undergraduate music students often experience a high learning curve when they first encounter pitch-class set theory, an analytical system very different from those they have studied previously. Students sometimes find the abstractions of integer notation and the mathematical orientation of set theory foreign or even frightening (Kleppinger 2010), and the dissonance of the atonal repertoire studied often engenders their resistance (Root 2010). Pedagogical games can help mitigate student resistance and trepidation. Table games like Bingo (Gillespie 2000) and Poker (Gingerich 1991) have been adapted to suit college-level classes in music theory. Familiar television shows provide another source of pedagogical games; for example, Berry (2008; 2015) adapts the show Survivor to frame a unit on theory fundamentals. However, none of these pedagogical games engage pitch- class set theory during a multi-week unit of study. In my dissertation, I adapt the show Survivor to frame a four-week unit on pitch- class set theory (introducing topics ranging from pitch-class sets to twelve-tone rows) during a sophomore-level theory course. As on the show, students of different achievement levels work together in small groups, or “tribes,” to complete worksheets called “challenges”; however, in an important modification to the structure of the show, no students are voted out of their tribes.
    [Show full text]
  • Music in Theory and Practice
    CHAPTER 4 Chords Harmony Primary Triads Roman Numerals TOPICS Chord Triad Position Simple Position Triad Root Position Third Inversion Tertian First Inversion Realization Root Second Inversion Macro Analysis Major Triad Seventh Chords Circle Progression Minor Triad Organum Leading-Tone Progression Diminished Triad Figured Bass Lead Sheet or Fake Sheet Augmented Triad IMPORTANT In the previous chapter, pairs of pitches were assigned specifi c names for identifi cation CONCEPTS purposes. The phenomenon of tones sounding simultaneously frequently includes group- ings of three, four, or more pitches. As with intervals, identifi cation names are assigned to larger tone groupings with specifi c symbols. Harmony is the musical result of tones sounding together. Whereas melody implies the Harmony linear or horizontal aspect of music, harmony refers to the vertical dimension of music. A chord is a harmonic unit with at least three different tones sounding simultaneously. Chord The term includes all possible such sonorities. Figure 4.1 #w w w w w bw & w w w bww w ww w w w w w w w‹ Strictly speaking, a triad is any three-tone chord. However, since western European music Triad of the seventeenth through the nineteenth centuries is tertian (chords containing a super- position of harmonic thirds), the term has come to be limited to a three-note chord built in superposed thirds. The term root refers to the note on which a triad is built. “C major triad” refers to a major Triad Root triad whose root is C. The root is the pitch from which a triad is generated. 73 3711_ben01877_Ch04pp73-94.indd 73 4/10/08 3:58:19 PM Four types of triads are in common use.
    [Show full text]