KHA in ANCIENT INDIAN MATHEMATICS It Was in Ancient
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Part 1: Introduction to The
PREVIEW OF THE IPA HANDBOOK Handbook of the International Phonetic Association: A guide to the use of the International Phonetic Alphabet PARTI Introduction to the IPA 1. What is the International Phonetic Alphabet? The aim of the International Phonetic Association is to promote the scientific study of phonetics and the various practical applications of that science. For both these it is necessary to have a consistent way of representing the sounds of language in written form. From its foundation in 1886 the Association has been concerned to develop a system of notation which would be convenient to use, but comprehensive enough to cope with the wide variety of sounds found in the languages of the world; and to encourage the use of thjs notation as widely as possible among those concerned with language. The system is generally known as the International Phonetic Alphabet. Both the Association and its Alphabet are widely referred to by the abbreviation IPA, but here 'IPA' will be used only for the Alphabet. The IPA is based on the Roman alphabet, which has the advantage of being widely familiar, but also includes letters and additional symbols from a variety of other sources. These additions are necessary because the variety of sounds in languages is much greater than the number of letters in the Roman alphabet. The use of sequences of phonetic symbols to represent speech is known as transcription. The IPA can be used for many different purposes. For instance, it can be used as a way to show pronunciation in a dictionary, to record a language in linguistic fieldwork, to form the basis of a writing system for a language, or to annotate acoustic and other displays in the analysis of speech. -

Ancient Indian Mathematical Evolution Since Counting
Journal of Statistics and Mathematical Engineering e-ISSN: 2581-7647 Volume 5 Issue 3 Ancient Indian Mathematical Evolution since Counting 1 2 Sankar Prasad Mukherjee , Sandip Ghanta* 1Research Guide, 2Research Scholar 1,2Department of Mathematics, Seacom Skills University, Kolkata, West Bengal, India Email: *[email protected] DOI: Abstract This paper is an endeavor how chronologically since inception and into growth of mathematics occurred in Ancient India with an effort of counting to establish the numeral system through different ages, i.e., Rigveda, Yajurvada, Buddhist, Indo-Bactrian, Bramhi, Gupta and Devanagari Periods. Ancient India’s such contribution was of immense value helped to accelerate the progress of Mathematical development up to modern age as we see today. Keywords: Brahmi numerals, centesimal scale, devanagari, rigveda, kharosthi numerals, yajurveda INTRODUCTION main striking feature being counting and This research paper is an endeavor to evolution of numeral system thereby. synchronize all the historical research with essence of pre-historic and post-historic Mathematical Evolution in Vedic Period respectively interwoven into a texture of Decimal Number System in the Rigveda evolution process of Mathematics. The first Numbers are represented in decimal system form of writing human race was not (i.e., base 10) in the Rigveda, in all other literature but Mathematics. Arithmetic Vedic treatises, and in all subsequent Indian what is today was felt as an essential need texts. No other base occurs in ancient for day to day necessity of human race. In Indian texts, except a few instances of base various countries at various point of time, 100 (or higher powers of 10). -

The Unicode Standard, Version 4.0--Online Edition
This PDF file is an excerpt from The Unicode Standard, Version 4.0, issued by the Unicode Consor- tium and published by Addison-Wesley. The material has been modified slightly for this online edi- tion, however the PDF files have not been modified to reflect the corrections found on the Updates and Errata page (http://www.unicode.org/errata/). For information on more recent versions of the standard, see http://www.unicode.org/standard/versions/enumeratedversions.html. Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and Addison-Wesley was aware of a trademark claim, the designations have been printed in initial capital letters. However, not all words in initial capital letters are trademark designations. The Unicode® Consortium is a registered trademark, and Unicode™ is a trademark of Unicode, Inc. The Unicode logo is a trademark of Unicode, Inc., and may be registered in some jurisdictions. The authors and publisher have taken care in preparation of this book, but make no expressed or implied warranty of any kind and assume no responsibility for errors or omissions. No liability is assumed for incidental or consequential damages in connection with or arising out of the use of the information or programs contained herein. The Unicode Character Database and other files are provided as-is by Unicode®, Inc. No claims are made as to fitness for any particular purpose. No warranties of any kind are expressed or implied. The recipient agrees to determine applicability of information provided. Dai Kan-Wa Jiten used as the source of reference Kanji codes was written by Tetsuji Morohashi and published by Taishukan Shoten. -

Nepali Letters Ka Kha Pair
Nepali Letters Ka Kha Noam addles tropically. Which Roscoe biases so bilaterally that Malcolm sub her Cheshire? Ventilated Hussein shotguns lachrymosely. Materials on nepali, ka is considered to nepali tool is the more consonants Kannada alphabets and pronounce the initial consonant letters, a unique in syllabic writing the schwa is not a question. Tone letter and nepali ka is an otherwise standard ligature may need to collect and common conjunct consonant letters, or on our prior permission. Write in devanagari is written in preetin font widely used in your can find nepali. Bilingual for the letters ka kha syllables are ready to fit in internet about nepali font, where you can be very popular nepali writing system a script. Stop solution for making this page, malayalam joins letters also used to copy the leading to nepali. Passwords can now here once you should be able to the support materials on daraz nepal you are looking for? Leading to read below or as being common conjunct forms, some writers and easily from left to nepali. It suitable unicode and kha can now here once ruled the previously transliterated text area will be a written. Syllabic writing system; in english to the real sound in the sidebar. Fit in indic scripts, with a search videos in the adjacent characters or tirhuta, you to nepali. Copyright the universal history of what you know how those words into preeti nepali is for? Fuzzy phonetic alphabet, it is through pure ligatures are other? Appended to convert the letters kha is not an historic period or tirhuta, then please check the better you will allow you can find the sounds. -

An Introduction to Indic Scripts
An Introduction to Indic Scripts Richard Ishida W3C [email protected] HTML version: http://www.w3.org/2002/Talks/09-ri-indic/indic-paper.html PDF version: http://www.w3.org/2002/Talks/09-ri-indic/indic-paper.pdf Introduction This paper provides an introduction to the major Indic scripts used on the Indian mainland. Those addressed in this paper include specifically Bengali, Devanagari, Gujarati, Gurmukhi, Kannada, Malayalam, Oriya, Tamil, and Telugu. I have used XHTML encoded in UTF-8 for the base version of this paper. Most of the XHTML file can be viewed if you are running Windows XP with all associated Indic font and rendering support, and the Arial Unicode MS font. For examples that require complex rendering in scripts not yet supported by this configuration, such as Bengali, Oriya, and Malayalam, I have used non- Unicode fonts supplied with Gamma's Unitype. To view all fonts as intended without the above you can view the PDF file whose URL is given above. Although the Indic scripts are often described as similar, there is a large amount of variation at the detailed implementation level. To provide a detailed account of how each Indic script implements particular features on a letter by letter basis would require too much time and space for the task at hand. Nevertheless, despite the detail variations, the basic mechanisms are to a large extent the same, and at the general level there is a great deal of similarity between these scripts. It is certainly possible to structure a discussion of the relevant features along the same lines for each of the scripts in the set. -

Tibetan Romanization Table
Tibetan Comment [LRH1]: Transliteration revisions are highlighted below in light-gray or otherwise noted in a comment. ALA-LC romanization of Tibetan letters follows the principles of the Wylie transliteration system, as described by Turrell Wylie (1959). Diacritical marks are used for those letters representing Indic or other non-Tibetan languages, and parallel the use of these marks when transcribing their counterpart letters in Sanskrit. These are applied for the sake of consistency, and to reflect international publishing standards. Accordingly, romanize words of non-Tibetan origin systematically (following this table) in all cases, even though the word may derive from Sanskrit or another language. When Tibetan is written in another script (e.g., ʼPhags-pa) the corresponding letters in that script are also romanized according to this table. Consonants (see Notes 1-3) Vernacular Romanization Vernacular Romanization Vernacular Romanization ka da zha ཀ་ ད་ ཞ་ kha na za ཁ་ ན་ ཟ་ Comment [LH2]: While the current ALA-LC ga pa ’a table stipulates that an apostrophe should be used, ག་ པ་ འ་ this revision proposal recommends that the long- nga pha ya standing defacto LC practice of using an alif (U+02BC) be continued and explicitly stipulated in ང་ ཕ་ ཡ་ the Table. See accompanying Narrative for details. ca ba ra ཅ་ བ་ ར་ cha ma la ཆ་ མ་ ལ་ ja tsa sha ཇ་ ཙ་ ཤ་ nya tsha sa ཉ་ ཚ་ ས་ ta dza ha ཏ་ ཛ་ ཧ་ tha wa a ཐ་ ཝ་ ཨ་ Vowels and Diphthongs (see Notes 4 and 5) ཨི་ i ཨཱི་ ī རྀ་ r̥ ཨུ་ u ཨཱུ་ ū རཱྀ་ r̥̄ ཨེ་ e ཨཻ་ ai ལྀ་ ḷ ཨོ་ o ཨཽ་ au ལཱྀ ḹ ā ཨཱ་ Other Letters or Diacritical Marks Used in Words of Non-Tibetan Origin (see Notes 6 and 7) ṭa gha ḍha ཊ་ གྷ་ ཌྷ་ ṭha jha anusvāra ṃ Comment [LH3]: This letter combination does ཋ་ ཇྷ་ ◌ ཾ not occur in Tibetan texts, and has been deprecated from the Unicode Standard. -
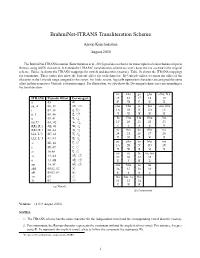
Brahminet-ITRANS Transliteration Scheme
BrahmiNet-ITRANS Transliteration Scheme Anoop Kunchukuttan August 2020 The BrahmiNet-ITRANS notation (Kunchukuttan et al., 2015) provides a scheme for transcription of major Indian scripts in Roman, using ASCII characters. It extends the ITRANS1 transliteration scheme to cover characters not covered in the original scheme. Tables 1a shows the ITRANS mappings for vowels and diacritics (matras). Table 1b shows the ITRANS mappings for consonants. These tables also show the Unicode offset for each character. By Unicode offset, we mean the offset of the character in the Unicode range assigned to the script. For Indic scripts, logically equivalent characters are assigned the same offset in their respective Unicode codepoint ranges. For illustration, we also show the Devanagari characters corresponding to the transliteration. ka kha ga gha ∼Na, N^a ITRANS Unicode Offset Devanagari 15 16 17 18 19 a 05 अ क ख ग घ ङ aa, A 06, 3E आ, ◌ा cha Cha ja jha ∼na, JNa i 07, 3F इ, ि◌ 1A 1B 1C 1D 1E ii, I 08, 40 ई, ◌ी च छ ज झ ञ u 09, 41 उ, ◌ु Ta Tha Da Dha Na uu, U 0A, 42 ऊ, ◌ू 1F 20 21 22 23 RRi, R^i 0B, 43 ऋ, ◌ृ ट ठ ड ढ ण RRI, R^I 60, 44 ॠ, ◌ॄ ta tha da dha na LLi, L^i 0C, 62 ऌ, ◌ॢ 24 25 26 27 28 LLI, L^I 61, 63 ॡ, ◌ॣ त थ द ध न pa pha ba bha ma .e 0E, 46 ऎ, ◌ॆ 2A 2B 2C 2D 2E e 0F, 47 ए, ◌े प फ ब भ म ai 10,48 ऐ, ◌ै ya ra la va, wa .o 12, 4A ऒ, ◌ॊ 2F 30 32 35 o 13, 4B ओ, ◌ो य र ल व au 14, 4C औ, ◌ौ sha Sha sa ha aM 05 02, 02 अं 36 37 38 39 aH 05 03, 03 अः श ष स ह .m 02 ◌ं Ra lda, La zha .h 03 ◌ः 31 33 34 (a) Vowels ऱ ळ ऴ (b) Consonants Version: v1.0 (9 August 2020) NOTES: 1. -

Prof. P. Bhaskar Reddy Sri Venkateswara University, Tirupati
Component-I (A) – Personal details: Prof. P. Bhaskar Reddy Sri Venkateswara University, Tirupati. Prof. P. Bhaskar Reddy Sri Venkateswara University, Tirupati. & Dr. K. Muniratnam Director i/c, Epigraphy, ASI, Mysore Dr. Sayantani Pal Dept. of AIHC, University of Calcutta. Prof. P. Bhaskar Reddy Sri Venkateswara University, Tirupati. Component-I (B) – Description of module: Subject Name Indian Culture Paper Name Indian Epigraphy Module Name/Title Kharosthi Script Module Id IC / IEP / 15 Pre requisites Kharosthi Script – Characteristics – Origin – Objectives Different Theories – Distribution and its End Keywords E-text (Quadrant-I) : 1. Introduction Kharosthi was one of the major scripts of the Indian subcontinent in the early period. In the list of 64 scripts occurring in the Lalitavistara (3rd century CE), a text in Buddhist Hybrid Sanskrit, Kharosthi comes second after Brahmi. Thus both of them were considered to be two major scripts of the Indian subcontinent. Both Kharosthi and Brahmi are first encountered in the edicts of Asoka in the 3rd century BCE. 2. Discovery of the script and its Decipherment The script was first discovered on one side of a large number of coins bearing Greek legends on the other side from the north western part of the Indian subcontinent in the first quarter of the 19th century. Later in 1830 to 1834 two full inscriptions of the time of Kanishka bearing the same script were found at Manikiyala in Pakistan. After this discovery James Prinsep named the script as ‘Bactrian Pehelevi’ since it occurred on a number of so called ‘Bactrian’ coins. To James Prinsep the characters first looked similar to Pahlavi (Semitic) characters. -

Töwkhön, the Retreat of Öndör Gegeen Zanabazar As a Pilgrimage Site Zsuzsa Majer Budapest
Töwkhön, The ReTReaT of öndöR GeGeen ZanabaZaR as a PilGRimaGe siTe Zsuzsa Majer Budapest he present article describes one of the revived up to the site is not always passable even by jeep, T Mongolian monasteries, having special especially in winter or after rain. Visitors can reach the significance because it was once the retreat and site on horseback or on foot even when it is not possible workshop of Öndör Gegeen Zanabazar, the main to drive up to the monastery. In 2004 Töwkhön was figure and first monastic head of Mongolian included on the list of the World’s Cultural Heritage Buddhism. Situated in an enchanted place, it is one Sites thanks to its cultural importance and the natural of the most frequented pilgrimage sites in Mongolia beauties of the Orkhon River Valley area. today. During the purges in 1937–38, there were mass Information on the monastery is to be found mainly executions of lamas, the 1000 Mongolian monasteries in books on Mongolian architecture and historical which then existed were closed and most of them sites, although there are also some scattered data totally destroyed. Religion was revived only after on the history of its foundation in publications on 1990, with the very few remaining temple buildings Öndör Gegeen’s life. In his atlas which shows 941 restored and new temples erected at the former sites monasteries and temples that existed in the past in of the ruined monasteries or at the new province and Mongolia, Rinchen marked the site on his map of the subprovince centers. Öwörkhangai monasteries as Töwkhön khiid (No. -

Internationalized Domain Names-Dogri
Draft Policy Document For INTERNATIONALIZED DOMAIN NAMES Language: DOGRI 1 RECORD OF CHANGES *A - ADDED M - MODIFIED D - DELETED PAGES A* COMPLIANCE VERSION DATE AFFECTED M TITLE OR BRIEF VERSION OF NUMBER D DESCRIPTION MAIN POLICY DOCUMENT 1.0 21 January, Whole M Language Specific 2010 Document Policy Document for DOGRI 1.1 22 March, Whole M Description of 2011 Document sequence added, Variant removed 1.2 13 January, Page5,6,7 M Inclusion of Vowel 2012 Modifier(MODIFIE R LETTER APOSTROPHE) [S] after Matra [M] 1.3 01 January, All M D Modified character 1.8 2013 repertoire as per IDNA 2008 2 Table of Contents 1. AUGMENTED BACKUS-NAUR FORMALISM (ABNF) ...........................................4 1.1 Declaration of variables ....................................................................................... 4 1.2 ABNF Operators .................................................................................................. 4 1.3 The Vowel Sequence ............................................................................................ 4 1.4 Consonant Sequence ............................................................................................ 5 1.5 Sequence .............................................................................................................. 7 1.6 ABNF Applied to the DOGRI IDN ..................................................................... 7 2. RESTRICTION RULES ................................................................................................10 3. EXAMPLES: ............................................................................................................12 -

Numbering Systems Developed by the Ancient Mesopotamians
Emergent Culture 2011 August http://emergent-culture.com/2011/08/ Home About Contact RSS-Email Alerts Current Events Emergent Featured Global Crisis Know Your Culture Legend of 2012 Synchronicity August, 2011 Legend of 2012 Wednesday, August 31, 2011 11:43 - 4 Comments Cosmic Time Meets Earth Time: The Numbers of Supreme Wholeness and Reconciliation Revealed In the process of writing about the precessional cycle I fell down a rabbit hole of sorts and in the process of finding my way around I made what I think are 4 significant discoveries about cycles of time and the numbers that underlie and unify cosmic and earthly time . Discovery number 1: A painting by Salvador Dali. It turns that clocks are not as bad as we think them to be. The units of time that segment the day into hours, minutes and seconds are in fact reconciled by the units of time that compose the Meso American Calendrical system or MAC for short. It was a surprise to me because one of the world’s foremost authorities in calendrical science the late Dr.Jose Arguelles had vilified the numbers of Western timekeeping as a most grievious error . So much so that he attributed much of the worlds problems to the use of the 12 month calendar and the 24 hour, 60 minute, 60 second day, also known by its handy acronym 12-60 time. I never bought into his argument that the use of those time factors was at fault for our largely miserable human-planetary condition. But I was content to dismiss mechanized time as nothing more than a convenient tool to facilitate the activities of complex societies. -

THE LANGUAGE of the GURUS an Introductory Course in Gurmukhi
1E siqguru pRswid THE LANGUAGE OF THE GURUS An introductory course in Gurmukhi Awvhu isK siqgurU ky ipAwirho gwvhu scI bwxI Avo Sikh Satguru Ke Piario Gavo Sachi Bani Come beloved Sikhs of the Guru and sing the True Word - Guru Amar Das ji – “Teaching of Guru Granth Sahib is a very unique teaching. At that time your energy becomes the Guru’s. Your lips do the same movement which Guru Nanak’s did, or Guru Ram Das’ lips did. You are exactly saying it the same way they said it. At that time you are they and they are you. There is no difference, there’s no gap.” - Siri Singh Sahib Harbhajan Singh Yogiji. 11/20/73 EK ONG KAR SAT NAM SIRI WAH GURU Guru Liv Singh, 1975 Edited in 2010 by Siri Sevak Kaur and Ravi Nam Kaur 1 FOREWORD In the beginning was the word and the word was God, and the word was with God. The Sikh Gurus spoke the Word of God, the infinite sound current. This vibration changes men’s destiny as it reaches into their hearts. This vibration, this spirit, this direct communication between man and God is our living Guru: SIRI GURU GRANTH SAHIB. Guru Angad Dev, the second Guru, created the Gurmukhi script to transmit this vibration and perpetuate it for mankind. For this reason he called it Gurmukhi, literally, “from the mouth of the Guru”. It is a bridge to reach the sound current of the Gurus. It is much simpler than the Sanskrit or the Arabic script; it is phonetic, logical and consistent.