Naïve Bayes Classifier
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Practical Statistics for Particle Physics Lecture 1 AEPS2018, Quy Nhon, Vietnam
Practical Statistics for Particle Physics Lecture 1 AEPS2018, Quy Nhon, Vietnam Roger Barlow The University of Huddersfield August 2018 Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 1 / 34 Lecture 1: The Basics 1 Probability What is it? Frequentist Probability Conditional Probability and Bayes' Theorem Bayesian Probability 2 Probability distributions and their properties Expectation Values Binomial, Poisson and Gaussian 3 Hypothesis testing Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 2 / 34 Question: What is Probability? Typical exam question Q1 Explain what is meant by the Probability PA of an event A [1] Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 3 / 34 Four possible answers PA is number obeying certain mathematical rules. PA is a property of A that determines how often A happens For N trials in which A occurs NA times, PA is the limit of NA=N for large N PA is my belief that A will happen, measurable by seeing what odds I will accept in a bet. Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 4 / 34 Mathematical Kolmogorov Axioms: For all A ⊂ S PA ≥ 0 PS = 1 P(A[B) = PA + PB if A \ B = ϕ and A; B ⊂ S From these simple axioms a complete and complicated structure can be − ≤ erected. E.g. show PA = 1 PA, and show PA 1.... But!!! This says nothing about what PA actually means. Kolmogorov had frequentist probability in mind, but these axioms apply to any definition. Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 5 / 34 Classical or Real probability Evolved during the 18th-19th century Developed (Pascal, Laplace and others) to serve the gambling industry. -
3.3 Bayes' Formula
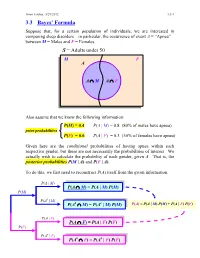
Ismor Fischer, 5/29/2012 3.3-1 3.3 Bayes’ Formula Suppose that, for a certain population of individuals, we are interested in comparing sleep disorders – in particular, the occurrence of event A = “Apnea” – between M = Males and F = Females. S = Adults under 50 M F A A ∩ M A ∩ F Also assume that we know the following information: P(M) = 0.4 P(A | M) = 0.8 (80% of males have apnea) prior probabilities P(F) = 0.6 P(A | F) = 0.3 (30% of females have apnea) Given here are the conditional probabilities of having apnea within each respective gender, but these are not necessarily the probabilities of interest. We actually wish to calculate the probability of each gender, given A. That is, the posterior probabilities P(M | A) and P(F | A). To do this, we first need to reconstruct P(A) itself from the given information. P(A | M) P(A ∩ M) = P(A | M) P(M) P(M) P(Ac | M) c c P(A ∩ M) = P(A | M) P(M) P(A) = P(A | M) P(M) + P(A | F) P(F) P(A | F) P(A ∩ F) = P(A | F) P(F) P(F) P(Ac | F) c c P(A ∩ F) = P(A | F) P(F) Ismor Fischer, 5/29/2012 3.3-2 So, given A… P(M ∩ A) P(A | M) P(M) P(M | A) = P(A) = P(A | M) P(M) + P(A | F) P(F) (0.8)(0.4) 0.32 = (0.8)(0.4) + (0.3)(0.6) = 0.50 = 0.64 and posterior P(F ∩ A) P(A | F) P(F) P(F | A) = = probabilities P(A) P(A | M) P(M) + P(A | F) P(F) (0.3)(0.6) 0.18 = (0.8)(0.4) + (0.3)(0.6) = 0.50 = 0.36 S Thus, the additional information that a M F randomly selected individual has apnea (an A event with probability 50% – why?) increases the likelihood of being male from a prior probability of 40% to a posterior probability 0.32 0.18 of 64%, and likewise, decreases the likelihood of being female from a prior probability of 60% to a posterior probability of 36%. -

On Discriminative Bayesian Network Classifiers and Logistic Regression
On Discriminative Bayesian Network Classifiers and Logistic Regression Teemu Roos and Hannes Wettig Complex Systems Computation Group, Helsinki Institute for Information Technology, P.O. Box 9800, FI-02015 HUT, Finland Peter Gr¨unwald Centrum voor Wiskunde en Informatica, P.O. Box 94079, NL-1090 GB Amsterdam, The Netherlands Petri Myllym¨aki and Henry Tirri Complex Systems Computation Group, Helsinki Institute for Information Technology, P.O. Box 9800, FI-02015 HUT, Finland Abstract. Discriminative learning of the parameters in the naive Bayes model is known to be equivalent to a logistic regression problem. Here we show that the same fact holds for much more general Bayesian network models, as long as the corresponding network structure satisfies a certain graph-theoretic property. The property holds for naive Bayes but also for more complex structures such as tree-augmented naive Bayes (TAN) as well as for mixed diagnostic-discriminative structures. Our results imply that for networks satisfying our property, the condi- tional likelihood cannot have local maxima so that the global maximum can be found by simple local optimization methods. We also show that if this property does not hold, then in general the conditional likelihood can have local, non-global maxima. We illustrate our theoretical results by empirical experiments with local optimization in a conditional naive Bayes model. Furthermore, we provide a heuristic strategy for pruning the number of parameters and relevant features in such models. For many data sets, we obtain good results with heavily pruned submodels containing many fewer parameters than the original naive Bayes model. Keywords: Bayesian classifiers, Bayesian networks, discriminative learning, logistic regression 1. -

Lecture 5: Naive Bayes Classifier 1 Introduction
CSE517A Machine Learning Spring 2020 Lecture 5: Naive Bayes Classifier Instructor: Marion Neumann Scribe: Jingyu Xin Reading: fcml 5.2.1 (Bayes Classifier, Naive Bayes, Classifying Text, and Smoothing) Application Sentiment analysis aims at discovering people's opinions, emo- tions, feelings about a subject matter, product, or service from text. Take some time to answer the following warm-up questions: (1) Is this a regression or classification problem? (2) What are the features and how would you represent them? (3) What is the prediction task? (4) How well do you think a linear model will perform? 1 Introduction Thought: Can we model p(y j x) without model assumptions, e.g. Gaussian/Bernoulli distribution etc.? Idea: Estimate p(y j x) from the data directly, then use the Bayes classifier. Let y be discrete, Pn i=1 I(xi = x \ yi = y) p(y j x) = Pn (1) i=1 I(xi = x) where the numerator counts all examples with input x that have label y and the denominator counts all examples with input x. Figure 1: Illustration of estimatingp ^(y j x) From Figure ??, it is clear that, using the MLE method, we can estimatep ^(y j x) as jCj p^(y j x) = (2) jBj But there is a big problem with this method: The MLE estimate is only good if there are many training vectors with the same identical features as x. 1 2 This never happens for high-dimensional or continuous feature spaces. Solution: Bayes Rule. p(x j y) p(y) p(y j x) = (3) p(x) Let's estimate p(x j y) and p(y) instead! 2 Naive Bayes We have a discrete label space C that can either be binary f+1; −1g or multi-class f1; :::; Kg. -

Numerical Physics with Probabilities: the Monte Carlo Method and Bayesian Statistics Part I for Assignment 2
Numerical Physics with Probabilities: The Monte Carlo Method and Bayesian Statistics Part I for Assignment 2 Department of Physics, University of Surrey module: Energy, Entropy and Numerical Physics (PHY2063) 1 Numerical Physics part of Energy, Entropy and Numerical Physics This numerical physics course is part of the second-year Energy, Entropy and Numerical Physics mod- ule. It is online at the EENP module on SurreyLearn. See there for assignments, deadlines etc. The course is about numerically solving ODEs (ordinary differential equations) and PDEs (partial differential equations), and introducing the (large) part of numerical physics where probabilities are used. This assignment is on numerical physics of probabilities, and looks at the Monte Carlo (MC) method, and at the Bayesian statistics approach to data analysis. It covers MC and Bayesian statistics, in that order. MC is a widely used numerical technique, it is used, amongst other things, for modelling many random processes. MC is used in fields from statistical physics, to nuclear and particle physics. Bayesian statistics is a powerful data analysis method, and is used everywhere from particle physics to spam-email filters. Data analysis is fundamental to science. For example, analysis of the data from the Large Hadron Collider was required to extract a most probable value for the mass of the Higgs boson, together with an estimate of the region of masses where the scientists think the mass is. This region is typically expressed as a range of mass values where the they think the true mass lies with high (e.g., 95%) probability. Many of you will be analysing data (physics data, commercial data, etc) for your PTY or RY, or future careers1 . -

The Bayesian Approach to Statistics
THE BAYESIAN APPROACH TO STATISTICS ANTHONY O’HAGAN INTRODUCTION the true nature of scientific reasoning. The fi- nal section addresses various features of modern By far the most widely taught and used statisti- Bayesian methods that provide some explanation for the rapid increase in their adoption since the cal methods in practice are those of the frequen- 1980s. tist school. The ideas of frequentist inference, as set out in Chapter 5 of this book, rest on the frequency definition of probability (Chapter 2), BAYESIAN INFERENCE and were developed in the first half of the 20th century. This chapter concerns a radically differ- We first present the basic procedures of Bayesian ent approach to statistics, the Bayesian approach, inference. which depends instead on the subjective defini- tion of probability (Chapter 3). In some respects, Bayesian methods are older than frequentist ones, Bayes’s Theorem and the Nature of Learning having been the basis of very early statistical rea- Bayesian inference is a process of learning soning as far back as the 18th century. Bayesian from data. To give substance to this statement, statistics as it is now understood, however, dates we need to identify who is doing the learning and back to the 1950s, with subsequent development what they are learning about. in the second half of the 20th century. Over that time, the Bayesian approach has steadily gained Terms and Notation ground, and is now recognized as a legitimate al- ternative to the frequentist approach. The person doing the learning is an individual This chapter is organized into three sections. -

Hybrid of Naive Bayes and Gaussian Naive Bayes for Classification: a Map Reduce Approach
International Journal of Innovative Technology and Exploring Engineering (IJITEE) ISSN: 2278-3075, Volume-8, Issue-6S3, April 2019 Hybrid of Naive Bayes and Gaussian Naive Bayes for Classification: A Map Reduce Approach Shikha Agarwal, Balmukumd Jha, Tisu Kumar, Manish Kumar, Prabhat Ranjan Abstract: Naive Bayes classifier is well known machine model could be used without accepting Bayesian probability learning algorithm which has shown virtues in many fields. In or using any Bayesian methods. Despite their naive design this work big data analysis platforms like Hadoop distributed and simple assumptions, Naive Bayes classifiers have computing and map reduce programming is used with Naive worked quite well in many complex situations. An analysis Bayes and Gaussian Naive Bayes for classification. Naive Bayes is manily popular for classification of discrete data sets while of the Bayesian classification problem showed that there are Gaussian is used to classify data that has continuous attributes. sound theoretical reasons behind the apparently implausible Experimental results show that Hybrid of Naive Bayes and efficacy of types of classifiers[5]. A comprehensive Gaussian Naive Bayes MapReduce model shows the better comparison with other classification algorithms in 2006 performance in terms of classification accuracy on adult data set showed that Bayes classification is outperformed by other which has many continuous attributes. approaches, such as boosted trees or random forests [6]. An Index Terms: Naive Bayes, Gaussian Naive Bayes, Map Reduce, Classification. advantage of Naive Bayes is that it only requires a small number of training data to estimate the parameters necessary I. INTRODUCTION for classification. The fundamental property of Naive Bayes is that it works on discrete value. -

Locally Differentially Private Naive Bayes Classification
Locally Differentially Private Naive Bayes Classification EMRE YILMAZ, Case Western Reserve University MOHAMMAD AL-RUBAIE, University of South Florida J. MORRIS CHANG, University of South Florida In machine learning, classification models need to be trained in order to predict class labels. When the training data contains personal information about individuals, collecting training data becomes difficult due to privacy concerns. Local differential privacy isa definition to measure the individual privacy when there is no trusted data curator. Individuals interact with an untrusteddata aggregator who obtains statistical information about the population without learning personal data. In order to train a Naive Bayes classifier in an untrusted setting, we propose to use methods satisfying local differential privacy. Individuals send theirperturbed inputs that keep the relationship between the feature values and class labels. The data aggregator estimates all probabilities needed by the Naive Bayes classifier. Then, new instances can be classified based on the estimated probabilities. We propose solutions forboth discrete and continuous data. In order to eliminate high amount of noise and decrease communication cost in multi-dimensional data, we propose utilizing dimensionality reduction techniques which can be applied by individuals before perturbing their inputs. Our experimental results show that the accuracy of the Naive Bayes classifier is maintained even when the individual privacy is guaranteed under local differential privacy, and that using dimensionality reduction enhances the accuracy. CCS Concepts: • Security and privacy → Privacy-preserving protocols; • Computing methodologies → Supervised learning by classification; Dimensionality reduction and manifold learning. Additional Key Words and Phrases: Local Differential Privacy, Naive Bayes, Classification, Dimensionality Reduction 1 INTRODUCTION Predictive analytics is the process of making prediction about future events by analyzing the current data using statistical techniques. -

Improving Feature Selection Algorithms Using Normalised Feature Histograms
Page 1 of 10 Improving feature selection algorithms using normalised feature histograms A. P. James and A. K. Maan The proposed feature selection method builds a histogram of the most stable features from random subsets of training set and ranks the features based on a classifier based cross validation. This approach reduces the instability of features obtained by conventional feature selection methods that occur with variation in training data and selection criteria. Classification results on 4 microarray and 3 image datasets using 3 major feature selection criteria and a naive bayes classifier show considerable improvement over benchmark results. Introduction : Relevance of features selected by conventional feature selection method is tightly coupled with the notion of inter-feature redundancy within the patterns [1-3]. This essentially results in design of data-driven methods that are designed for meeting criteria of redundancy using various measures of inter-feature correlations [4-5]. These measures behave differently to different types of data, and to different levels of natural variability. This introduces instability in selection of features with change in number of samples in the training set and quality of features from one database to another. The use of large number of statistically distinct training samples can increase the quality of the selected features, although it can be practically unrealistic due to increase in computational complexity and unavailability of sufficient training samples. As an example, in realistic high dimensional databases such as gene expression databases of a rare cancer, there is a practical limitation on availability of large number of training samples. In such cases, instability that occurs with selecting features from insufficient training data would lead to a wrong conclusion that genes responsible for a cancer be strongly subject dependent and not general for a cancer. -

Paradoxes and Priors in Bayesian Regression
Paradoxes and Priors in Bayesian Regression Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Agniva Som, B. Stat., M. Stat. Graduate Program in Statistics The Ohio State University 2014 Dissertation Committee: Dr. Christopher M. Hans, Advisor Dr. Steven N. MacEachern, Co-advisor Dr. Mario Peruggia c Copyright by Agniva Som 2014 Abstract The linear model has been by far the most popular and most attractive choice of a statistical model over the past century, ubiquitous in both frequentist and Bayesian literature. The basic model has been gradually improved over the years to deal with stronger features in the data like multicollinearity, non-linear or functional data pat- terns, violation of underlying model assumptions etc. One valuable direction pursued in the enrichment of the linear model is the use of Bayesian methods, which blend information from the data likelihood and suitable prior distributions placed on the unknown model parameters to carry out inference. This dissertation studies the modeling implications of many common prior distri- butions in linear regression, including the popular g prior and its recent ameliorations. Formalization of desirable characteristics for model comparison and parameter esti- mation has led to the growth of appropriate mixtures of g priors that conform to the seven standard model selection criteria laid out by Bayarri et al. (2012). The existence of some of these properties (or lack thereof) is demonstrated by examining the behavior of the prior under suitable limits on the likelihood or on the prior itself. -

Naïve Bayes Lecture 17
Naïve Bayes Lecture 17 David Sontag New York University Slides adapted from Luke Zettlemoyer, Carlos Guestrin, Dan Klein, and Mehryar Mohri Brief ArticleBrief Article The Author The Author January 11, 2012January 11, 2012 θˆ =argmax ln P ( θ) θˆ =argmax ln P ( θ) θ D| θ D| ln θαH ln θαH d d d ln P ( θ)= [ln θαH (1 θ)αT ] = [α ln θ + α ln(1 θ)] d d dθ D| dθ d − dθ H T − ln P ( θ)= [ln θαH (1 θ)αT ] = [α ln θ + α ln(1 θ)] dθ D| dθ − dθ H T − d d αH αT = αH ln θ + αT ln(1 θ)= =0 d d dθ αH dθ αT− θ − 1 θ = αH ln θ + αT ln(1 θ)= =0 − dθ dθ − θ −2N12 θ δ 2e− − P (mistake) ≥ ≥ 2N2 δ 2e− P (mistake) ≥ ≥ ln δ ln 2 2N2 Bayesian Learning ≥ − Prior • Use Bayes’ rule! 2 Data Likelihood ln δ ln 2 2N ln(2/δ) ≥ − N ≥ 22 Posterior ln(2/δ) N ln(2/0.05) 3.8 ≥ 22N Normalization= 190 ≥ 2 0.12 ≈ 0.02 × ln(2• /Or0. equivalently:05) 3.8 N • For uniform priors, this= 190 reducesP (θ) to 1 ≥ 2 0.12 ≈ 0.02 ∝ ×maximum likelihood estimation! P (θ) 1 P (θ ) P ( θ) ∝ |D ∝ D| 1 1 Brief ArticleBrief Article Brief Article Brief Article The Author The Author The Author January 11, 2012 JanuaryThe Author 11, 2012 January 11, 2012 January 11, 2012 θˆ =argmax ln Pθˆ( =argmaxθ) ln P ( θ) θ D| θ D| ˆ =argmax ln (θˆ =argmax) ln P ( θ) θ P θ θ θ D| αH D| ln θαH ln θ αH ln θαH ln θ d d α α d d d lnαP ( θ)=α [lndθ H (1 θ) T ] = [α ln θ + α ln(1 θ)] ln P ( θ)= [lndθ H (1 θ) T ]d= [α ln θ + α ln(1d Hθ)] T d d dθ D| dθ d αH H − αT T dθ − dθ D| dθ αlnH P ( − θα)=T [lndθθ (1 θ) ] = [α−H ln θ + αT ln(1 θ)] ln P ( θ)= [lndθθ (1 D|θ) ] =dθ [αH ln θ−+ αT ln(1dθ θ)] − dθ D| dθ − d dθ d −α -

A Widely Applicable Bayesian Information Criterion
JournalofMachineLearningResearch14(2013)867-897 Submitted 8/12; Revised 2/13; Published 3/13 A Widely Applicable Bayesian Information Criterion Sumio Watanabe [email protected] Department of Computational Intelligence and Systems Science Tokyo Institute of Technology Mailbox G5-19, 4259 Nagatsuta, Midori-ku Yokohama, Japan 226-8502 Editor: Manfred Opper Abstract A statistical model or a learning machine is called regular if the map taking a parameter to a prob- ability distribution is one-to-one and if its Fisher information matrix is always positive definite. If otherwise, it is called singular. In regular statistical models, the Bayes free energy, which is defined by the minus logarithm of Bayes marginal likelihood, can be asymptotically approximated by the Schwarz Bayes information criterion (BIC), whereas in singular models such approximation does not hold. Recently, it was proved that the Bayes free energy of a singular model is asymptotically given by a generalized formula using a birational invariant, the real log canonical threshold (RLCT), instead of half the number of parameters in BIC. Theoretical values of RLCTs in several statistical models are now being discovered based on algebraic geometrical methodology. However, it has been difficult to estimate the Bayes free energy using only training samples, because an RLCT depends on an unknown true distribution. In the present paper, we define a widely applicable Bayesian information criterion (WBIC) by the average log likelihood function over the posterior distribution with the inverse temperature 1/logn, where n is the number of training samples. We mathematically prove that WBIC has the same asymptotic expansion as the Bayes free energy, even if a statistical model is singular for or unrealizable by a statistical model.