Generalized Naive Bayes Classifiers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Descriptive Statistics (Part 2): Interpreting Study Results
Statistical Notes II Descriptive statistics (Part 2): Interpreting study results A Cook and A Sheikh he previous paper in this series looked at ‘baseline’. Investigations of treatment effects can be descriptive statistics, showing how to use and made in similar fashion by comparisons of disease T interpret fundamental measures such as the probability in treated and untreated patients. mean and standard deviation. Here we continue with descriptive statistics, looking at measures more The relative risk (RR), also sometimes known as specific to medical research. We start by defining the risk ratio, compares the risk of exposed and risk and odds, the two basic measures of disease unexposed subjects, while the odds ratio (OR) probability. Then we show how the effect of a disease compares odds. A relative risk or odds ratio greater risk factor, or a treatment, can be measured using the than one indicates an exposure to be harmful, while relative risk or the odds ratio. Finally we discuss the a value less than one indicates a protective effect. ‘number needed to treat’, a measure derived from the RR = 1.2 means exposed people are 20% more likely relative risk, which has gained popularity because of to be diseased, RR = 1.4 means 40% more likely. its clinical usefulness. Examples from the literature OR = 1.2 means that the odds of disease is 20% higher are used to illustrate important concepts. in exposed people. RISK AND ODDS Among workers at factory two (‘exposed’ workers) The probability of an individual becoming diseased the risk is 13 / 116 = 0.11, compared to an ‘unexposed’ is the risk. -

Teacher Guide 12.1 Gambling Page 1
TEACHER GUIDE 12.1 GAMBLING PAGE 1 Standard 12: The student will explain and evaluate the financial impact and consequences of gambling. Risky Business Priority Academic Student Skills Personal Financial Literacy Objective 12.1: Analyze the probabilities involved in winning at games of chance. Objective 12.2: Evaluate costs and benefits of gambling to Simone, Paula, and individuals and society (e.g., family budget; addictive behaviors; Randy meet in the library and the local and state economy). every afternoon to work on their homework. Here is what is going on. Ryan is flipping a coin, and he is not cheating. He has just flipped seven heads in a row. Is Ryan’s next flip more likely to be: Heads; Tails; or Heads and tails are equally likely. Paula says heads because the first seven were heads, so the next one will probably be heads too. Randy says tails. The first seven were heads, so the next one must be tails. Lesson Objectives Simone says that it could be either heads or tails Recognize gambling as a form of risk. because both are equally Calculate the probabilities of winning in games of chance. likely. Who is correct? Explore the potential benefits of gambling for society. Explore the potential costs of gambling for society. Evaluate the personal costs and benefits of gambling. © 2008. Oklahoma State Department of Education. All rights reserved. Teacher Guide 12.1 2 Personal Financial Literacy Vocabulary Dependent event: The outcome of one event affects the outcome of another, changing the TEACHING TIP probability of the second event. This lesson is based on risk. -

Odds: Gambling, Law and Strategy in the European Union Anastasios Kaburakis* and Ryan M Rodenberg†
63 Odds: Gambling, Law and Strategy in the European Union Anastasios Kaburakis* and Ryan M Rodenberg† Contemporary business law contributions argue that legal knowledge or ‘legal astuteness’ can lead to a sustainable competitive advantage.1 Past theses and treatises have led more academic research to endeavour the confluence between law and strategy.2 European scholars have engaged in the Proactive Law Movement, recently adopted and incorporated into policy by the European Commission.3 As such, the ‘many futures of legal strategy’ provide * Dr Anastasios Kaburakis is an assistant professor at the John Cook School of Business, Saint Louis University, teaching courses in strategic management, sports business and international comparative gaming law. He holds MS and PhD degrees from Indiana University-Bloomington and a law degree from Aristotle University in Thessaloniki, Greece. Prior to academia, he practised law in Greece and coached basketball at the professional club and national team level. He currently consults international sport federations, as well as gaming operators on regulatory matters and policy compliance strategies. † Dr Ryan Rodenberg is an assistant professor at Florida State University where he teaches sports law analytics. He earned his JD from the University of Washington-Seattle and PhD from Indiana University-Bloomington. Prior to academia, he worked at Octagon, Nike and the ATP World Tour. 1 See C Bagley, ‘What’s Law Got to Do With It?: Integrating Law and Strategy’ (2010) 47 American Business Law Journal 587; C -
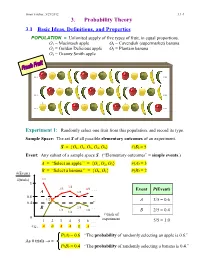
3. Probability Theory
Ismor Fischer, 5/29/2012 3.1-1 3. Probability Theory 3.1 Basic Ideas, Definitions, and Properties POPULATION = Unlimited supply of five types of fruit, in equal proportions. O1 = Macintosh apple O4 = Cavendish (supermarket) banana O2 = Golden Delicious apple O5 = Plantain banana O3 = Granny Smith apple … … … … … … Experiment 1: Randomly select one fruit from this population, and record its type. Sample Space: The set S of all possible elementary outcomes of an experiment. S = {O1, O2, O3, O4, O5} #(S) = 5 Event: Any subset of a sample space S. (“Elementary outcomes” = simple events.) A = “Select an apple.” = {O1, O2, O3} #(A) = 3 B = “Select a banana.” = {O , O } #(B) = 2 #(Event) 4 5 #(trials) 1/1 1 3/4 2/3 4/6 . Event P(Event) A 3/5 0.6 1/2 A 3/5 = 0.6 0.4 B 2/5 . 1/3 2/6 1/4 B 2/5 = 0.4 # trials of 0 experiment 1 2 3 4 5 6 . 5/5 = 1.0 e.g., A B A A B A . P(A) = 0.6 “The probability of randomly selecting an apple is 0.6.” As # trials → ∞ P(B) = 0.4 “The probability of randomly selecting a banana is 0.4.” Ismor Fischer, 5/29/2012 3.1-2 General formulation may be facilitated with the use of a Venn diagram: Experiment ⇒ Sample Space: S = {O1, O2, …, Ok} #(S) = k A Om+1 Om+2 O2 O1 O3 Om+3 O 4 . Om . Ok Event A = {O1, O2, …, Om} ⊆ S #(A) = m ≤ k Definition: The probability of event A, denoted P(A), is the long-run relative frequency with which A is expected to occur, as the experiment is repeated indefinitely. -

On Discriminative Bayesian Network Classifiers and Logistic Regression
On Discriminative Bayesian Network Classifiers and Logistic Regression Teemu Roos and Hannes Wettig Complex Systems Computation Group, Helsinki Institute for Information Technology, P.O. Box 9800, FI-02015 HUT, Finland Peter Gr¨unwald Centrum voor Wiskunde en Informatica, P.O. Box 94079, NL-1090 GB Amsterdam, The Netherlands Petri Myllym¨aki and Henry Tirri Complex Systems Computation Group, Helsinki Institute for Information Technology, P.O. Box 9800, FI-02015 HUT, Finland Abstract. Discriminative learning of the parameters in the naive Bayes model is known to be equivalent to a logistic regression problem. Here we show that the same fact holds for much more general Bayesian network models, as long as the corresponding network structure satisfies a certain graph-theoretic property. The property holds for naive Bayes but also for more complex structures such as tree-augmented naive Bayes (TAN) as well as for mixed diagnostic-discriminative structures. Our results imply that for networks satisfying our property, the condi- tional likelihood cannot have local maxima so that the global maximum can be found by simple local optimization methods. We also show that if this property does not hold, then in general the conditional likelihood can have local, non-global maxima. We illustrate our theoretical results by empirical experiments with local optimization in a conditional naive Bayes model. Furthermore, we provide a heuristic strategy for pruning the number of parameters and relevant features in such models. For many data sets, we obtain good results with heavily pruned submodels containing many fewer parameters than the original naive Bayes model. Keywords: Bayesian classifiers, Bayesian networks, discriminative learning, logistic regression 1. -

Probability Cheatsheet V2.0 Thinking Conditionally Law of Total Probability (LOTP)
Probability Cheatsheet v2.0 Thinking Conditionally Law of Total Probability (LOTP) Let B1;B2;B3; :::Bn be a partition of the sample space (i.e., they are Compiled by William Chen (http://wzchen.com) and Joe Blitzstein, Independence disjoint and their union is the entire sample space). with contributions from Sebastian Chiu, Yuan Jiang, Yuqi Hou, and Independent Events A and B are independent if knowing whether P (A) = P (AjB )P (B ) + P (AjB )P (B ) + ··· + P (AjB )P (B ) Jessy Hwang. Material based on Joe Blitzstein's (@stat110) lectures 1 1 2 2 n n A occurred gives no information about whether B occurred. More (http://stat110.net) and Blitzstein/Hwang's Introduction to P (A) = P (A \ B1) + P (A \ B2) + ··· + P (A \ Bn) formally, A and B (which have nonzero probability) are independent if Probability textbook (http://bit.ly/introprobability). Licensed and only if one of the following equivalent statements holds: For LOTP with extra conditioning, just add in another event C! under CC BY-NC-SA 4.0. Please share comments, suggestions, and errors at http://github.com/wzchen/probability_cheatsheet. P (A \ B) = P (A)P (B) P (AjC) = P (AjB1;C)P (B1jC) + ··· + P (AjBn;C)P (BnjC) P (AjB) = P (A) P (AjC) = P (A \ B1jC) + P (A \ B2jC) + ··· + P (A \ BnjC) P (BjA) = P (B) Last Updated September 4, 2015 Special case of LOTP with B and Bc as partition: Conditional Independence A and B are conditionally independent P (A) = P (AjB)P (B) + P (AjBc)P (Bc) given C if P (A \ BjC) = P (AjC)P (BjC). -

Understanding Relative Risk, Odds Ratio, and Related Terms: As Simple As It Can Get Chittaranjan Andrade, MD
Understanding Relative Risk, Odds Ratio, and Related Terms: As Simple as It Can Get Chittaranjan Andrade, MD Each month in his online Introduction column, Dr Andrade Many research papers present findings as odds ratios (ORs) and considers theoretical and relative risks (RRs) as measures of effect size for categorical outcomes. practical ideas in clinical Whereas these and related terms have been well explained in many psychopharmacology articles,1–5 this article presents a version, with examples, that is meant with a view to update the knowledge and skills to be both simple and practical. Readers may note that the explanations of medical practitioners and examples provided apply mostly to randomized controlled trials who treat patients with (RCTs), cohort studies, and case-control studies. Nevertheless, similar psychiatric conditions. principles operate when these concepts are applied in epidemiologic Department of Psychopharmacology, National Institute research. Whereas the terms may be applied slightly differently in of Mental Health and Neurosciences, Bangalore, India different explanatory texts, the general principles are the same. ([email protected]). ABSTRACT Clinical Situation Risk, and related measures of effect size (for Consider a hypothetical RCT in which 76 depressed patients were categorical outcomes) such as relative risks and randomly assigned to receive either venlafaxine (n = 40) or placebo odds ratios, are frequently presented in research (n = 36) for 8 weeks. During the trial, new-onset sexual dysfunction articles. Not all readers know how these statistics was identified in 8 patients treated with venlafaxine and in 3 patients are derived and interpreted, nor are all readers treated with placebo. These results are presented in Table 1. -

Lecture 5: Naive Bayes Classifier 1 Introduction
CSE517A Machine Learning Spring 2020 Lecture 5: Naive Bayes Classifier Instructor: Marion Neumann Scribe: Jingyu Xin Reading: fcml 5.2.1 (Bayes Classifier, Naive Bayes, Classifying Text, and Smoothing) Application Sentiment analysis aims at discovering people's opinions, emo- tions, feelings about a subject matter, product, or service from text. Take some time to answer the following warm-up questions: (1) Is this a regression or classification problem? (2) What are the features and how would you represent them? (3) What is the prediction task? (4) How well do you think a linear model will perform? 1 Introduction Thought: Can we model p(y j x) without model assumptions, e.g. Gaussian/Bernoulli distribution etc.? Idea: Estimate p(y j x) from the data directly, then use the Bayes classifier. Let y be discrete, Pn i=1 I(xi = x \ yi = y) p(y j x) = Pn (1) i=1 I(xi = x) where the numerator counts all examples with input x that have label y and the denominator counts all examples with input x. Figure 1: Illustration of estimatingp ^(y j x) From Figure ??, it is clear that, using the MLE method, we can estimatep ^(y j x) as jCj p^(y j x) = (2) jBj But there is a big problem with this method: The MLE estimate is only good if there are many training vectors with the same identical features as x. 1 2 This never happens for high-dimensional or continuous feature spaces. Solution: Bayes Rule. p(x j y) p(y) p(y j x) = (3) p(x) Let's estimate p(x j y) and p(y) instead! 2 Naive Bayes We have a discrete label space C that can either be binary f+1; −1g or multi-class f1; :::; Kg. -

Hybrid of Naive Bayes and Gaussian Naive Bayes for Classification: a Map Reduce Approach
International Journal of Innovative Technology and Exploring Engineering (IJITEE) ISSN: 2278-3075, Volume-8, Issue-6S3, April 2019 Hybrid of Naive Bayes and Gaussian Naive Bayes for Classification: A Map Reduce Approach Shikha Agarwal, Balmukumd Jha, Tisu Kumar, Manish Kumar, Prabhat Ranjan Abstract: Naive Bayes classifier is well known machine model could be used without accepting Bayesian probability learning algorithm which has shown virtues in many fields. In or using any Bayesian methods. Despite their naive design this work big data analysis platforms like Hadoop distributed and simple assumptions, Naive Bayes classifiers have computing and map reduce programming is used with Naive worked quite well in many complex situations. An analysis Bayes and Gaussian Naive Bayes for classification. Naive Bayes is manily popular for classification of discrete data sets while of the Bayesian classification problem showed that there are Gaussian is used to classify data that has continuous attributes. sound theoretical reasons behind the apparently implausible Experimental results show that Hybrid of Naive Bayes and efficacy of types of classifiers[5]. A comprehensive Gaussian Naive Bayes MapReduce model shows the better comparison with other classification algorithms in 2006 performance in terms of classification accuracy on adult data set showed that Bayes classification is outperformed by other which has many continuous attributes. approaches, such as boosted trees or random forests [6]. An Index Terms: Naive Bayes, Gaussian Naive Bayes, Map Reduce, Classification. advantage of Naive Bayes is that it only requires a small number of training data to estimate the parameters necessary I. INTRODUCTION for classification. The fundamental property of Naive Bayes is that it works on discrete value. -

Locally Differentially Private Naive Bayes Classification
Locally Differentially Private Naive Bayes Classification EMRE YILMAZ, Case Western Reserve University MOHAMMAD AL-RUBAIE, University of South Florida J. MORRIS CHANG, University of South Florida In machine learning, classification models need to be trained in order to predict class labels. When the training data contains personal information about individuals, collecting training data becomes difficult due to privacy concerns. Local differential privacy isa definition to measure the individual privacy when there is no trusted data curator. Individuals interact with an untrusteddata aggregator who obtains statistical information about the population without learning personal data. In order to train a Naive Bayes classifier in an untrusted setting, we propose to use methods satisfying local differential privacy. Individuals send theirperturbed inputs that keep the relationship between the feature values and class labels. The data aggregator estimates all probabilities needed by the Naive Bayes classifier. Then, new instances can be classified based on the estimated probabilities. We propose solutions forboth discrete and continuous data. In order to eliminate high amount of noise and decrease communication cost in multi-dimensional data, we propose utilizing dimensionality reduction techniques which can be applied by individuals before perturbing their inputs. Our experimental results show that the accuracy of the Naive Bayes classifier is maintained even when the individual privacy is guaranteed under local differential privacy, and that using dimensionality reduction enhances the accuracy. CCS Concepts: • Security and privacy → Privacy-preserving protocols; • Computing methodologies → Supervised learning by classification; Dimensionality reduction and manifold learning. Additional Key Words and Phrases: Local Differential Privacy, Naive Bayes, Classification, Dimensionality Reduction 1 INTRODUCTION Predictive analytics is the process of making prediction about future events by analyzing the current data using statistical techniques. -

Improving Feature Selection Algorithms Using Normalised Feature Histograms
Page 1 of 10 Improving feature selection algorithms using normalised feature histograms A. P. James and A. K. Maan The proposed feature selection method builds a histogram of the most stable features from random subsets of training set and ranks the features based on a classifier based cross validation. This approach reduces the instability of features obtained by conventional feature selection methods that occur with variation in training data and selection criteria. Classification results on 4 microarray and 3 image datasets using 3 major feature selection criteria and a naive bayes classifier show considerable improvement over benchmark results. Introduction : Relevance of features selected by conventional feature selection method is tightly coupled with the notion of inter-feature redundancy within the patterns [1-3]. This essentially results in design of data-driven methods that are designed for meeting criteria of redundancy using various measures of inter-feature correlations [4-5]. These measures behave differently to different types of data, and to different levels of natural variability. This introduces instability in selection of features with change in number of samples in the training set and quality of features from one database to another. The use of large number of statistically distinct training samples can increase the quality of the selected features, although it can be practically unrealistic due to increase in computational complexity and unavailability of sufficient training samples. As an example, in realistic high dimensional databases such as gene expression databases of a rare cancer, there is a practical limitation on availability of large number of training samples. In such cases, instability that occurs with selecting features from insufficient training data would lead to a wrong conclusion that genes responsible for a cancer be strongly subject dependent and not general for a cancer. -

Naïve Bayes Lecture 17
Naïve Bayes Lecture 17 David Sontag New York University Slides adapted from Luke Zettlemoyer, Carlos Guestrin, Dan Klein, and Mehryar Mohri Brief ArticleBrief Article The Author The Author January 11, 2012January 11, 2012 θˆ =argmax ln P ( θ) θˆ =argmax ln P ( θ) θ D| θ D| ln θαH ln θαH d d d ln P ( θ)= [ln θαH (1 θ)αT ] = [α ln θ + α ln(1 θ)] d d dθ D| dθ d − dθ H T − ln P ( θ)= [ln θαH (1 θ)αT ] = [α ln θ + α ln(1 θ)] dθ D| dθ − dθ H T − d d αH αT = αH ln θ + αT ln(1 θ)= =0 d d dθ αH dθ αT− θ − 1 θ = αH ln θ + αT ln(1 θ)= =0 − dθ dθ − θ −2N12 θ δ 2e− − P (mistake) ≥ ≥ 2N2 δ 2e− P (mistake) ≥ ≥ ln δ ln 2 2N2 Bayesian Learning ≥ − Prior • Use Bayes’ rule! 2 Data Likelihood ln δ ln 2 2N ln(2/δ) ≥ − N ≥ 22 Posterior ln(2/δ) N ln(2/0.05) 3.8 ≥ 22N Normalization= 190 ≥ 2 0.12 ≈ 0.02 × ln(2• /Or0. equivalently:05) 3.8 N • For uniform priors, this= 190 reducesP (θ) to 1 ≥ 2 0.12 ≈ 0.02 ∝ ×maximum likelihood estimation! P (θ) 1 P (θ ) P ( θ) ∝ |D ∝ D| 1 1 Brief ArticleBrief Article Brief Article Brief Article The Author The Author The Author January 11, 2012 JanuaryThe Author 11, 2012 January 11, 2012 January 11, 2012 θˆ =argmax ln Pθˆ( =argmaxθ) ln P ( θ) θ D| θ D| ˆ =argmax ln (θˆ =argmax) ln P ( θ) θ P θ θ θ D| αH D| ln θαH ln θ αH ln θαH ln θ d d α α d d d lnαP ( θ)=α [lndθ H (1 θ) T ] = [α ln θ + α ln(1 θ)] ln P ( θ)= [lndθ H (1 θ) T ]d= [α ln θ + α ln(1d Hθ)] T d d dθ D| dθ d αH H − αT T dθ − dθ D| dθ αlnH P ( − θα)=T [lndθθ (1 θ) ] = [α−H ln θ + αT ln(1 θ)] ln P ( θ)= [lndθθ (1 D|θ) ] =dθ [αH ln θ−+ αT ln(1dθ θ)] − dθ D| dθ − d dθ d −α