DOCSLIB.ORG

Probability Cheatsheet V2.0 Thinking Conditionally Law of Total Probability (LOTP)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Probability Cheatsheet V2.0 Thinking Conditionally Law of Total Probability (LOTP) Probability Cheatsheet v2.0 Thinking Conditionally Law of Total Probability (LOTP) Let B1;B2;B3; :::Bn be a partition of the sample space (i.e., they are Compiled by William Chen (http://wzchen.com) and Joe Blitzstein, Independence disjoint and their union is the entire sample space). with contributions from Sebastian Chiu, Yuan Jiang, Yuqi Hou, and Independent Events A and B are independent if knowing whether P (A) = P (AjB )P (B ) + P (AjB )P (B ) + ··· + P (AjB )P (B ) Jessy Hwang. Material based on Joe Blitzstein's (@stat110) lectures 1 1 2 2 n n A occurred gives no information about whether B occurred. More (http://stat110.net) and Blitzstein/Hwang's Introduction to P (A) = P (A \ B1) + P (A \ B2) + ··· + P (A \ Bn) formally, A and B (which have nonzero probability) are independent if Probability textbook (http://bit.ly/introprobability). Licensed and only if one of the following equivalent statements holds: For LOTP with extra conditioning, just add in another event C! under CC BY-NC-SA 4.0. Please share comments, suggestions, and errors at http://github.com/wzchen/probability_cheatsheet. P (A \ B) = P (A)P (B) P (AjC) = P (AjB1;C)P (B1jC) + ··· + P (AjBn;C)P (BnjC) P (AjB) = P (A) P (AjC) = P (A \ B1jC) + P (A \ B2jC) + ··· + P (A \ BnjC) P (BjA) = P (B) Last Updated September 4, 2015 Special case of LOTP with B and Bc as partition: Conditional Independence A and B are conditionally independent P (A) = P (AjB)P (B) + P (AjBc)P (Bc) given C if P (A \ BjC) = P (AjC)P (BjC). Conditional independence Counting does not imply independence, and independence does not imply P (A) = P (A \ B) + P (A \ Bc) conditional independence. Multiplication Rule Unions, Intersections, and Complements Bayes' Rule De Morgan's Laws A useful identity that can make calculating Bayes' Rule, and with extra conditioning (just add in C!) C probabilities of unions easier by relating them to intersections, and cake V vice versa. Analogous results hold with more than two sets. P (BjA)P (A) C waffl S e c c c P (AjB) = cake (A [ B) = A \ B P (B) cake V c c c (A \ B) = A [ B P (BjA; C)P (AjC) waffl wa e P (AjB; C) = ffl C S e P (BjC) V cake Joint, Marginal, and Conditional S We can also write wa ffle Joint Probability P (A \ B) or P (A; B) { Probability of A and B. P (A; B; C) P (B; CjA)P (A) P (AjB; C) = = Let's say we have a compound experiment (an experiment with Marginal (Unconditional) Probability P (A) { Probability of A. P (B; C) P (B; C) multiple components). If the 1st component has n1 possible outcomes, Conditional Probability P (AjB) = P (A; B)=P (B) { Probability of the 2nd component has n2 possible outcomes, . , and the rth A, given that B occurred. Odds Form of Bayes' Rule component has nr possible outcomes, then overall there are Conditional Probability is Probability P (AjB) is a probability P (AjB) P (BjA) P (A) n1n2 : : : nr possibilities for the whole experiment. = function for any fixed B. Any theorem that holds for probability also P (AcjB) P (BjAc) P (Ac) holds for conditional probability. Sampling Table The posterior odds of A are the likelihood ratio times the prior odds. Probability of an Intersection or Union Intersections via Conditioning Random Variables and their Distributions P (A; B) = P (A)P (BjA) PMF, CDF, and Independence P (A; B; C) = P (A)P (BjA)P (CjA; B) Probability Mass Function (PMF) Gives the probability that a Unions via Inclusion-Exclusion 2 8 discrete random variable takes on the value x. 5 P (A [ B) = P (A) + P (B) − P (A \ B) 7 9 pX (x) = P (X = x) 1 4 P (A [ B [ C) = P (A) + P (B) + P (C) 3 6 − P (A \ B) − P (A \ C) − P (B \ C) The sampling table gives the number of possible samples of size k out + P (A \ B \ C): of a population of size n, under various assumptions about how the 1.0 sample is collected. Simpson's Paradox 0.8 Order Matters Not Matter 0.6 heart k n + k − 1 pmf With Replacement n ● k 0.4 n! n ● ● Without Replacement (n − k)! k 0.2 ● ● band-aid 0.0 Naive Definition of Probability 0 1 2 3 4 If all outcomes are equally likely, the probability of an event A Dr. Hibbert Dr. Nick x It is possible to have happening is: The PMF satisfies c c c c P (A j B; C) < P (A j B ;C) and P (A j B; C ) < P (A j B ;C ) X number of outcomes favorable to A pX (x) ≥ 0 and pX (x) = 1 Pnaive(A) = c number of outcomes yet also P (A j B) > P (A j B ): x Cumulative Distribution Function (CDF) Gives the probability Indicator Random Variables LOTUS that a random variable is less than or equal to x. Indicator Random Variable is a random variable that takes on the Expected value of a function of an r.v. The expected value of X FX (x) = P (X ≤ x) value 1 or 0. It is always an indicator of some event: if the event is defined this way: occurs, the indicator is 1; otherwise it is 0. They are useful for many problems about counting how many events of some kind occur. Write X E(X) = xP (X = x) (for discrete X) ( x ● 1 if A occurs, 1.0 IA = ● ● 0 if A does not occur. Z 1 E(X) = xf(x)dx (for continuous X) 0.8 2 −∞ ● ● Note that IA = IA;IAIB = IA\B ; and IA[B = IA + IB − IAIB . The Law of the Unconscious Statistician (LOTUS) states that 0.6 Distribution IA ∼ Bern(p) where p = P (A). you can find the expected value of a function of a random variable, cdf Fundamental Bridge The expectation of the indicator for event A is g(X), in a similar way, by replacing the x in front of the PMF/PDF by 0.4 ● ● g(x) but still working with the PMF/PDF of X: the probability of event A: E(IA) = P (A). 0.2 X E(g(X)) = g(x)P (X = x) (for discrete X) ● ● Variance and Standard Deviation ● x 0.0 Var(X) = E (X − E(X))2 = E(X2) − (E(X))2 0 1 2 3 4 Z 1 q E(g(X)) = g(x)f(x)dx (for continuous X) x SD(X) = Var(X) −∞ The CDF is an increasing, right-continuous function with Continuous RVs, LOTUS, UoU What's a function of a random variable? A function of a random variable is also a random variable. For example, if X is the number of F (x) ! 0 as x ! −∞ and F (x) ! 1 as x ! 1 X X bikes you see in an hour, then g(X) = 2X is the number of bike wheels Independence Intuitively, two random variables are independent if X X(X−1) Continuous Random Variables (CRVs) you see in that hour and h(X) = 2 = 2 is the number of knowing the value of one gives no information about the other. pairs of bikes such that you see both of those bikes in that hour. Discrete r.v.s X and Y are independent if for all values of x and y What's the probability that a CRV is in an interval? Take the difference in CDF values (or use the PDF as described later). What's the point? You don't need to know the PMF/PDF of g(X) P (X = x; Y = y) = P (X = x)P (Y = y) to find its expected value. All you need is the PMF/PDF of X. P (a ≤ X ≤ b) = P (X ≤ b) − P (X ≤ a) = F (b) − F (a) Expected Value and Indicators X X For X ∼ N (µ, σ2), this becomes Universality of Uniform (UoU) Expected Value and Linearity b − µ a − µ When you plug any CRV into its own CDF, you get a Uniform(0,1) P (a ≤ X ≤ b) = Φ − Φ random variable. When you plug a Uniform(0,1) r.v. into an inverse Expected Value (a.k.a. mean, expectation, or average) is a weighted σ σ CDF, you get an r.v. with that CDF. For example, let's say that a average of the possible outcomes of our random variable. random variable X has CDF Mathematically, if x1; x2; x3;::: are all of the distinct possible values What is the Probability Density Function (PDF)? The PDF f that X can take, the expected value of X is is the derivative of the CDF F . −x F (x) = 1 − e ; for x > 0 P E(X) = xiP (X = xi) F 0(x) = f(x) i By UoU, if we plug X into this function then we get a uniformly distributed random variable. X Y X + Y A PDF is nonnegative and integrates to 1. By the fundamental theorem of calculus, to get from PDF back to CDF we can integrate: 3 4 7 F (X) = 1 − e−X ∼ Unif(0; 1) 2 2 4 Z x 6 8 14 F (x) = f(t)dt Similarly, if U ∼ Unif(0; 1) then F −1(U) has CDF F . The key point is 10 23 33 −∞ 1 –3 –2 that for any continuous random variable X, we can transform it into a Uniform random variable and back by using its CDF.
Load more

Recommended publications
  • Descriptive Statistics (Part 2): Interpreting Study Results
    Statistical Notes II Descriptive statistics (Part 2): Interpreting study results A Cook and A Sheikh he previous paper in this series looked at ‘baseline’. Investigations of treatment effects can be descriptive statistics, showing how to use and made in similar fashion by comparisons of disease T interpret fundamental measures such as the probability in treated and untreated patients. mean and standard deviation. Here we continue with descriptive statistics, looking at measures more The relative risk (RR), also sometimes known as specific to medical research. We start by defining the risk ratio, compares the risk of exposed and risk and odds, the two basic measures of disease unexposed subjects, while the odds ratio (OR) probability. Then we show how the effect of a disease compares odds. A relative risk or odds ratio greater risk factor, or a treatment, can be measured using the than one indicates an exposure to be harmful, while relative risk or the odds ratio. Finally we discuss the a value less than one indicates a protective effect. ‘number needed to treat’, a measure derived from the RR = 1.2 means exposed people are 20% more likely relative risk, which has gained popularity because of to be diseased, RR = 1.4 means 40% more likely. its clinical usefulness. Examples from the literature OR = 1.2 means that the odds of disease is 20% higher are used to illustrate important concepts. in exposed people. RISK AND ODDS Among workers at factory two (‘exposed’ workers) The probability of an individual becoming diseased the risk is 13 / 116 = 0.11, compared to an ‘unexposed’ is the risk.
    [Show full text]
  • Teacher Guide 12.1 Gambling Page 1
    TEACHER GUIDE 12.1 GAMBLING PAGE 1 Standard 12: The student will explain and evaluate the financial impact and consequences of gambling. Risky Business Priority Academic Student Skills Personal Financial Literacy Objective 12.1: Analyze the probabilities involved in winning at games of chance. Objective 12.2: Evaluate costs and benefits of gambling to Simone, Paula, and individuals and society (e.g., family budget; addictive behaviors; Randy meet in the library and the local and state economy). every afternoon to work on their homework. Here is what is going on. Ryan is flipping a coin, and he is not cheating. He has just flipped seven heads in a row. Is Ryan’s next flip more likely to be: Heads; Tails; or Heads and tails are equally likely. Paula says heads because the first seven were heads, so the next one will probably be heads too. Randy says tails. The first seven were heads, so the next one must be tails. Lesson Objectives Simone says that it could be either heads or tails Recognize gambling as a form of risk. because both are equally Calculate the probabilities of winning in games of chance. likely. Who is correct? Explore the potential benefits of gambling for society. Explore the potential costs of gambling for society. Evaluate the personal costs and benefits of gambling. © 2008. Oklahoma State Department of Education. All rights reserved. Teacher Guide 12.1 2 Personal Financial Literacy Vocabulary Dependent event: The outcome of one event affects the outcome of another, changing the TEACHING TIP probability of the second event. This lesson is based on risk.
    [Show full text]
  • 18.440: Lecture 9 Expectations of Discrete Random Variables
    18.440: Lecture 9 Expectations of discrete random variables Scott Sheffield MIT 18.440 Lecture 9 1 Outline Defining expectation Functions of random variables Motivation 18.440 Lecture 9 2 Outline Defining expectation Functions of random variables Motivation 18.440 Lecture 9 3 Expectation of a discrete random variable I Recall: a random variable X is a function from the state space to the real numbers. I Can interpret X as a quantity whose value depends on the outcome of an experiment. I Say X is a discrete random variable if (with probability one) it takes one of a countable set of values. I For each a in this countable set, write p(a) := PfX = ag. Call p the probability mass function. I The expectation of X , written E [X ], is defined by X E [X ] = xp(x): x:p(x)>0 I Represents weighted average of possible values X can take, each value being weighted by its probability. 18.440 Lecture 9 4 Simple examples I Suppose that a random variable X satisfies PfX = 1g = :5, PfX = 2g = :25 and PfX = 3g = :25. I What is E [X ]? I Answer: :5 × 1 + :25 × 2 + :25 × 3 = 1:75. I Suppose PfX = 1g = p and PfX = 0g = 1 − p. Then what is E [X ]? I Answer: p. I Roll a standard six-sided die. What is the expectation of number that comes up? 1 1 1 1 1 1 21 I Answer: 6 1 + 6 2 + 6 3 + 6 4 + 6 5 + 6 6 = 6 = 3:5. 18.440 Lecture 9 5 Expectation when state space is countable II If the state space S is countable, we can give SUM OVER STATE SPACE definition of expectation: X E [X ] = PfsgX (s): s2S II Compare this to the SUM OVER POSSIBLE X VALUES definition we gave earlier: X E [X ] = xp(x): x:p(x)>0 II Example: toss two coins.
    [Show full text]
  • Odds: Gambling, Law and Strategy in the European Union Anastasios Kaburakis* and Ryan M Rodenberg†
    63 Odds: Gambling, Law and Strategy in the European Union Anastasios Kaburakis* and Ryan M Rodenberg† Contemporary business law contributions argue that legal knowledge or ‘legal astuteness’ can lead to a sustainable competitive advantage.1 Past theses and treatises have led more academic research to endeavour the confluence between law and strategy.2 European scholars have engaged in the Proactive Law Movement, recently adopted and incorporated into policy by the European Commission.3 As such, the ‘many futures of legal strategy’ provide * Dr Anastasios Kaburakis is an assistant professor at the John Cook School of Business, Saint Louis University, teaching courses in strategic management, sports business and international comparative gaming law. He holds MS and PhD degrees from Indiana University-Bloomington and a law degree from Aristotle University in Thessaloniki, Greece. Prior to academia, he practised law in Greece and coached basketball at the professional club and national team level. He currently consults international sport federations, as well as gaming operators on regulatory matters and policy compliance strategies. † Dr Ryan Rodenberg is an assistant professor at Florida State University where he teaches sports law analytics. He earned his JD from the University of Washington-Seattle and PhD from Indiana University-Bloomington. Prior to academia, he worked at Octagon, Nike and the ATP World Tour. 1 See C Bagley, ‘What’s Law Got to Do With It?: Integrating Law and Strategy’ (2010) 47 American Business Law Journal 587; C
    [Show full text]
  • Laws of Total Expectation and Total Variance
    Laws of Total Expectation and Total Variance Definition of conditional density. Assume and arbitrary random variable X with density fX . Take an event A with P (A) > 0. Then the conditional density fXjA is defined as follows: 8 < f(x) 2 P (A) x A fXjA(x) = : 0 x2 = A Note that the support of fXjA is supported only in A. Definition of conditional expectation conditioned on an event. Z Z 1 E(h(X)jA) = h(x) fXjA(x) dx = h(x) fX (x) dx A P (A) A Example. For the random variable X with density function 8 < 1 3 64 x 0 < x < 4 f(x) = : 0 otherwise calculate E(X2 j X ≥ 1). Solution. Step 1. Z h i 4 1 1 1 x=4 255 P (X ≥ 1) = x3 dx = x4 = 1 64 256 4 x=1 256 Step 2. Z Z ( ) 1 256 4 1 E(X2 j X ≥ 1) = x2 f(x) dx = x2 x3 dx P (X ≥ 1) fx≥1g 255 1 64 Z ( ) ( )( ) h i 256 4 1 256 1 1 x=4 8192 = x5 dx = x6 = 255 1 64 255 64 6 x=1 765 Definition of conditional variance conditioned on an event. Var(XjA) = E(X2jA) − E(XjA)2 1 Example. For the previous example , calculate the conditional variance Var(XjX ≥ 1) Solution. We already calculated E(X2 j X ≥ 1). We only need to calculate E(X j X ≥ 1). Z Z Z ( ) 1 256 4 1 E(X j X ≥ 1) = x f(x) dx = x x3 dx P (X ≥ 1) fx≥1g 255 1 64 Z ( ) ( )( ) h i 256 4 1 256 1 1 x=4 4096 = x4 dx = x5 = 255 1 64 255 64 5 x=1 1275 Finally: ( ) 8192 4096 2 630784 Var(XjX ≥ 1) = E(X2jX ≥ 1) − E(XjX ≥ 1)2 = − = 765 1275 1625625 Definition of conditional expectation conditioned on a random variable.
    [Show full text]
  • Randomized Algorithms
    Chapter 9 Randomized Algorithms randomized The theme of this chapter is madendrizo algorithms. These are algorithms that make use of randomness in their computation. You might know of quicksort, which is efficient on average when it uses a random pivot, but can be bad for any pivot that is selected without randomness. Analyzing randomized algorithms can be difficult, so you might wonder why randomiza- tion in algorithms is so important and worth the extra effort. Well it turns out that for certain problems randomized algorithms are simpler or faster than algorithms that do not use random- ness. The problem of primality testing (PT), which is to determine if an integer is prime, is a good example. In the late 70s Miller and Rabin developed a famous and simple random- ized algorithm for the problem that only requires polynomial work. For over 20 years it was not known whether the problem could be solved in polynomial work without randomization. Eventually a polynomial time algorithm was developed, but it is much more complicated and computationally more costly than the randomized version. Hence in practice everyone still uses the randomized version. There are many other problems in which a randomized solution is simpler or cheaper than the best non-randomized solution. In this chapter, after covering the prerequisite background, we will consider some such problems. The first we will consider is the following simple prob- lem: Question: How many comparisons do we need to find the top two largest numbers in a sequence of n distinct numbers? Without the help of randomization, there is a trivial algorithm for finding the top two largest numbers in a sequence that requires about 2n − 3 comparisons.
    [Show full text]
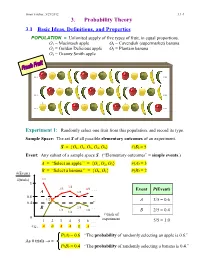
  • 3. Probability Theory
    Ismor Fischer, 5/29/2012 3.1-1 3. Probability Theory 3.1 Basic Ideas, Definitions, and Properties POPULATION = Unlimited supply of five types of fruit, in equal proportions. O1 = Macintosh apple O4 = Cavendish (supermarket) banana O2 = Golden Delicious apple O5 = Plantain banana O3 = Granny Smith apple … … … … … … Experiment 1: Randomly select one fruit from this population, and record its type. Sample Space: The set S of all possible elementary outcomes of an experiment. S = {O1, O2, O3, O4, O5} #(S) = 5 Event: Any subset of a sample space S. (“Elementary outcomes” = simple events.) A = “Select an apple.” = {O1, O2, O3} #(A) = 3 B = “Select a banana.” = {O , O } #(B) = 2 #(Event) 4 5 #(trials) 1/1 1 3/4 2/3 4/6 . Event P(Event) A 3/5 0.6 1/2 A 3/5 = 0.6 0.4 B 2/5 . 1/3 2/6 1/4 B 2/5 = 0.4 # trials of 0 experiment 1 2 3 4 5 6 . 5/5 = 1.0 e.g., A B A A B A . P(A) = 0.6 “The probability of randomly selecting an apple is 0.6.” As # trials → ∞ P(B) = 0.4 “The probability of randomly selecting a banana is 0.4.” Ismor Fischer, 5/29/2012 3.1-2 General formulation may be facilitated with the use of a Venn diagram: Experiment ⇒ Sample Space: S = {O1, O2, …, Ok} #(S) = k A Om+1 Om+2 O2 O1 O3 Om+3 O 4 . Om . Ok Event A = {O1, O2, …, Om} ⊆ S #(A) = m ≤ k Definition: The probability of event A, denoted P(A), is the long-run relative frequency with which A is expected to occur, as the experiment is repeated indefinitely.
    [Show full text]
  • Joint Probability Distributions
    ST 380 Probability and Statistics for the Physical Sciences Joint Probability Distributions In many experiments, two or more random variables have values that are determined by the outcome of the experiment. For example, the binomial experiment is a sequence of trials, each of which results in success or failure. If ( 1 if the i th trial is a success Xi = 0 otherwise; then X1; X2;:::; Xn are all random variables defined on the whole experiment. 1 / 15 Joint Probability Distributions Introduction ST 380 Probability and Statistics for the Physical Sciences To calculate probabilities involving two random variables X and Y such as P(X > 0 and Y ≤ 0); we need the joint distribution of X and Y . The way we represent the joint distribution depends on whether the random variables are discrete or continuous. 2 / 15 Joint Probability Distributions Introduction ST 380 Probability and Statistics for the Physical Sciences Two Discrete Random Variables If X and Y are discrete, with ranges RX and RY , respectively, the joint probability mass function is p(x; y) = P(X = x and Y = y); x 2 RX ; y 2 RY : Then a probability like P(X > 0 and Y ≤ 0) is just X X p(x; y): x2RX :x>0 y2RY :y≤0 3 / 15 Joint Probability Distributions Two Discrete Random Variables ST 380 Probability and Statistics for the Physical Sciences Marginal Distribution To find the probability of an event defined only by X , we need the marginal pmf of X : X pX (x) = P(X = x) = p(x; y); x 2 RX : y2RY Similarly the marginal pmf of Y is X pY (y) = P(Y = y) = p(x; y); y 2 RY : x2RX 4 / 15 Joint
    [Show full text]
  • Probability Cheatsheet
    Probability Cheatsheet v1.1.1 Simpson's Paradox Expected Value, Linearity, and Symmetry P (A j B; C) < P (A j Bc;C) and P (A j B; Cc) < P (A j Bc;Cc) Expected Value (aka mean, expectation, or average) can be thought Compiled by William Chen (http://wzchen.com) with contributions yet still, P (A j B) > P (A j Bc) of as the \weighted average" of the possible outcomes of our random from Sebastian Chiu, Yuan Jiang, Yuqi Hou, and Jessy Hwang. variable. Mathematically, if x1; x2; x3;::: are all of the possible values Material based off of Joe Blitzstein's (@stat110) lectures Bayes' Rule and Law of Total Probability that X can take, the expected value of X can be calculated as follows: P (http://stat110.net) and Blitzstein/Hwang's Intro to Probability E(X) = xiP (X = xi) textbook (http://bit.ly/introprobability). Licensed under CC i Law of Total Probability with partitioning set B1; B2; B3; :::Bn and BY-NC-SA 4.0. Please share comments, suggestions, and errors at with extra conditioning (just add C!) Note that for any X and Y , a and b scaling coefficients and c is our http://github.com/wzchen/probability_cheatsheet. constant, the following property of Linearity of Expectation holds: P (A) = P (AjB1)P (B1) + P (AjB2)P (B2) + :::P (AjBn)P (Bn) Last Updated March 20, 2015 P (A) = P (A \ B1) + P (A \ B2) + :::P (A \ Bn) E(aX + bY + c) = aE(X) + bE(Y ) + c P (AjC) = P (AjB1; C)P (B1jC) + :::P (AjBn; C)P (BnjC) If two Random Variables have the same distribution, even when they are dependent by the property of Symmetry their expected values P (AjC) = P (A \ B jC) + P (A \ B jC) + :::P (A \ B jC) Counting 1 2 n are equal.
    [Show full text]
  • 4. Stochas C Processes
    51 4. Stochasc processes Be able to formulate models for stochastic processes, and understand how they can be used for estimation and prediction. Be familiar with calculation techniques for memoryless stochastic processes. Understand the classification of discrete state space Markov chains, and be able to calculate the stationary distribution, and recognise limit theorems. Science is often concerned with the laws that describe how a system changes over time, such as Newton’s laws of motion. When we use probabilistic laws to describe how the system changes, the system is called a stochastic process. We used a stochastic process model in Section 1.2 to analyse Bitcoin; the probabilistic part of our model was the randomness of who generates the next Bitcoin block, be it the attacker or the rest of the peer-to-peer network. In Part II, you will come across stochastic process models in several courses: • in Computer Systems Modelling they are used to describe discrete event simulations of communications networks • in Machine Learning and Bayesian Inference they are used for computing posterior distributions • in Information Theory they are used to describe noisy communications channels, and also the data streams sent over such channels. 4.1. Markov chains Example 4.1. The Russian mathematician Andrei Markov (1856–1922) invented a new type of probabilistic model, now given his name, and his first application was to model Pushkin’s poem Eugeny Onegin. He suggested the following method for generating a stream of text C = (C ;C ;C ;::: ) where each C is an alphabetic character: 0 1 2 n As usual, we write C for the random 1 alphabet = [ ’a ’ , ’b ’ ,...] # a l l p o s s i b l e c h a r a c t e r s i n c l .
    [Show full text]
  • Functions of Random Variables
    Names for Eg(X ) Generating Functions Topic 8 The Expected Value Functions of Random Variables 1 / 19 Names for Eg(X ) Generating Functions Outline Names for Eg(X ) Means Moments Factorial Moments Variance and Standard Deviation Generating Functions 2 / 19 Names for Eg(X ) Generating Functions Means If g(x) = x, then µX = EX is called variously the distributional mean, and the first moment. • Sn, the number of successes in n Bernoulli trials with success parameter p, has mean np. • The mean of a geometric random variable with parameter p is (1 − p)=p . • The mean of an exponential random variable with parameter β is1 /β. • A standard normal random variable has mean0. Exercise. Find the mean of a Pareto random variable. Z 1 Z 1 βαβ Z 1 αββ 1 αβ xf (x) dx = x dx = βαβ x−β dx = x1−β = ; β > 1 x β+1 −∞ α x α 1 − β α β − 1 3 / 19 Names for Eg(X ) Generating Functions Moments In analogy to a similar concept in physics, EX m is called the m-th moment. The second moment in physics is associated to the moment of inertia. • If X is a Bernoulli random variable, then X = X m. Thus, EX m = EX = p. • For a uniform random variable on [0; 1], the m-th moment is R 1 m 0 x dx = 1=(m + 1). • The third moment for Z, a standard normal random, is0. The fourth moment, 1 Z 1 z2 1 z2 1 4 4 3 EZ = p z exp − dz = −p z exp − 2π −∞ 2 2π 2 −∞ 1 Z 1 z2 +p 3z2 exp − dz = 3EZ 2 = 3 2π −∞ 2 3 z2 u(z) = z v(t) = − exp − 2 0 2 0 z2 u (z) = 3z v (t) = z exp − 2 4 / 19 Names for Eg(X ) Generating Functions Factorial Moments If g(x) = (x)k , where( x)k = x(x − 1) ··· (x − k + 1), then E(X )k is called the k-th factorial moment.
    [Show full text]
  • 5 Stochastic Processes
    5 Stochastic Processes Contents 5.1. The Bernoulli Process ...................p.3 5.2. The Poisson Process .................. p.15 1 2 Stochastic Processes Chap. 5 A stochastic process is a mathematical model of a probabilistic experiment that evolves in time and generates a sequence of numerical values. For example, a stochastic process can be used to model: (a) the sequence of daily prices of a stock; (b) the sequence of scores in a football game; (c) the sequence of failure times of a machine; (d) the sequence of hourly traffic loads at a node of a communication network; (e) the sequence of radar measurements of the position of an airplane. Each numerical value in the sequence is modeled by a random variable, so a stochastic process is simply a (finite or infinite) sequence of random variables and does not represent a major conceptual departure from our basic framework. We are still dealing with a single basic experiment that involves outcomes gov- erned by a probability law, and random variables that inherit their probabilistic † properties from that law. However, stochastic processes involve some change in emphasis over our earlier models. In particular: (a) We tend to focus on the dependencies in the sequence of values generated by the process. For example, how do future prices of a stock depend on past values? (b) We are often interested in long-term averages,involving the entire se- quence of generated values. For example, what is the fraction of time that a machine is idle? (c) We sometimes wish to characterize the likelihood or frequency of certain boundary events.
    [Show full text]