Chapter 6 Modelling Results
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Heritage Impact Walkdown Report
2017/06/19 HERITAGE IMPACT WALKDOWN REPORT Heritage Impact Walkdown Report for the Construction of a Substation and 132kV Power Line from Heilbron (via Frankfort) to Villiers, Free state Province. Prepared By: Prepared For: i Substation and 132kV Powerline: Heilbron (via Frankfort) to Villiers 2017/06/19 CREDIT SHEET Project Director STEPHAN GAIGHER (BA Hons, Archaeology, UP) Principal Investigator for G&A Heritage Member of ASAPA (Site Director Status) Tel: (015) 516 1561 Cell: 073 752 6583 E-mail: [email protected] Website: www.gaheritage.co.za Report Author STEPHAN GAIGHER Disclaimer; This report is a first phase heritage investigation into the heritage sensitivity of the area demarcated for the project. The report is meant to be a guide for further fieldwork and is not meant to be totally encompassing. Information is derived solely from published works. Statement of Independence As the duly appointed representative of G&A Heritage, I Stephan Gaigher, hereby confirm my independence as a specialist and declare that neither I nor G&A Heritage have any interests, be it business or otherwise, in any proposed activity, application or appeal in respect of which the Environmental Consultant was appointed as Environmental Assessment Practitioner, other than fair remuneration for work performed on this project. I also; ü acted as the independent specialist in this application; ü regard the information contained in this report as it relates to my specialist input/study to be true and correct, and ü do not have and will not have any financial -

Idp Review 2020/21
IDP REVIEW 2019/20 IDP REVIEW 2020/21 NGWATHE LOCAL MUNICIPALITY IDP REVIEW 2020/21 POLITICAL LEADERSHIP CLLR MJ MOCHELA CLLR NP MOPEDI EXECUTIVE MAYOR SPEAKER WARD 1 WARD 2 WARD 3 WARD 4 CLLR MATROOS CLLR P NDAYI CLLR M MOFOKENG CLLR S NTEO WARD 5 WARD 8 WARD 6 WARD 7 CLLR R KGANTSE CLLR M RAPULENG CLLR M MAGASHULE CLLR M GOBIDOLO WARD 9 WARD 10 WARD 11 WARD 12 CLLR M MBELE CLLR M MOFOKENG CLLR N TLHOBELO CLLR A VREY WARD 13 WARD 14 WARD 15 WARD 16 CLLR H FIELAND CLLR R MEHLO CLLR MOFOKENG CLLR SOCHIVA WARD 17 WARD 18 CLLR M TAJE CLLR M TOYI 2 | P a g e NGWATHE LOCAL MUNICIPALITY IDP REVIEW 2020/21 PROPORTIONAL REPRESENTATIVE COUNCILLORS NAME & SURNAME PR COUNCILLORS POLITICAL PARTY Motlalepule Mochela PR ANC Neheng Mopedi PR ANC Mvulane Sonto PR ANC Matshepiso Mmusi PR ANC Mabatho Miyen PR ANC Maria Serathi PR ANC Victoria De Beer PR ANC Robert Ferendale PR DA Molaphene Polokoestsile PR DA Alfred Sehume PR DA Shirley Vermaack PR DA Carina Serfontein PR DA Arnold Schoonwinkel PR DA Pieter La Cock PR DA Caroline Tete PR EFF Bakwena Thene PR EFF Sylvia Radebe PR EFF Petrus Van Der Merwe PR VF 3 | P a g e NGWATHE LOCAL MUNICIPALITY IDP REVIEW 2020/21 TABLE OF CONTENTS SECTION TOPIC PAGE NO Political Leadership 2-3 Proportional Representative Councillors 3 Table of Contents 4 List of Tables 5-6 Table of Figure 7 Foreword By Executive Mayor 8 Overview By Municipal Manager 9-11 Executive Summary 12-14 SECTION A Introduction and Current Reality 16 Political governance and administration SECTON B Profile of the municipality 20 SECTION C Spatial -

Directory of Organisations and Resources for People with Disabilities in South Africa
DISABILITY ALL SORTS A DIRECTORY OF ORGANISATIONS AND RESOURCES FOR PEOPLE WITH DISABILITIES IN SOUTH AFRICA University of South Africa CONTENTS FOREWORD ADVOCACY — ALL DISABILITIES ADVOCACY — DISABILITY-SPECIFIC ACCOMMODATION (SUGGESTIONS FOR WORK AND EDUCATION) AIRLINES THAT ACCOMMODATE WHEELCHAIRS ARTS ASSISTANCE AND THERAPY DOGS ASSISTIVE DEVICES FOR HIRE ASSISTIVE DEVICES FOR PURCHASE ASSISTIVE DEVICES — MAIL ORDER ASSISTIVE DEVICES — REPAIRS ASSISTIVE DEVICES — RESOURCE AND INFORMATION CENTRE BACK SUPPORT BOOKS, DISABILITY GUIDES AND INFORMATION RESOURCES BRAILLE AND AUDIO PRODUCTION BREATHING SUPPORT BUILDING OF RAMPS BURSARIES CAREGIVERS AND NURSES CAREGIVERS AND NURSES — EASTERN CAPE CAREGIVERS AND NURSES — FREE STATE CAREGIVERS AND NURSES — GAUTENG CAREGIVERS AND NURSES — KWAZULU-NATAL CAREGIVERS AND NURSES — LIMPOPO CAREGIVERS AND NURSES — MPUMALANGA CAREGIVERS AND NURSES — NORTHERN CAPE CAREGIVERS AND NURSES — NORTH WEST CAREGIVERS AND NURSES — WESTERN CAPE CHARITY/GIFT SHOPS COMMUNITY SERVICE ORGANISATIONS COMPENSATION FOR WORKPLACE INJURIES COMPLEMENTARY THERAPIES CONVERSION OF VEHICLES COUNSELLING CRÈCHES DAY CARE CENTRES — EASTERN CAPE DAY CARE CENTRES — FREE STATE 1 DAY CARE CENTRES — GAUTENG DAY CARE CENTRES — KWAZULU-NATAL DAY CARE CENTRES — LIMPOPO DAY CARE CENTRES — MPUMALANGA DAY CARE CENTRES — WESTERN CAPE DISABILITY EQUITY CONSULTANTS DISABILITY MAGAZINES AND NEWSLETTERS DISABILITY MANAGEMENT DISABILITY SENSITISATION PROJECTS DISABILITY STUDIES DRIVING SCHOOLS E-LEARNING END-OF-LIFE DETERMINATION ENTREPRENEURIAL -

South Africa)
FREE STATE PROFILE (South Africa) Lochner Marais University of the Free State Bloemfontein, SA OECD Roundtable on Higher Education in Regional and City Development, 16 September 2010 [email protected] 1 Map 4.7: Areas with development potential in the Free State, 2006 Mining SASOLBURG Location PARYS DENEYSVILLE ORANJEVILLE VREDEFORT VILLIERS FREE STATE PROVINCIAL GOVERNMENT VILJOENSKROON KOPPIES CORNELIA HEILBRON FRANKFORT BOTHAVILLE Legend VREDE Towns EDENVILLE TWEELING Limited Combined Potential KROONSTAD Int PETRUS STEYN MEMEL ALLANRIDGE REITZ Below Average Combined Potential HOOPSTAD WESSELSBRON WARDEN ODENDAALSRUS Agric LINDLEY STEYNSRUST Above Average Combined Potential WELKOM HENNENMAN ARLINGTON VENTERSBURG HERTZOGVILLE VIRGINIA High Combined Potential BETHLEHEM Local municipality BULTFONTEIN HARRISMITH THEUNISSEN PAUL ROUX KESTELL SENEKAL PovertyLimited Combined Potential WINBURG ROSENDAL CLARENS PHUTHADITJHABA BOSHOF Below Average Combined Potential FOURIESBURG DEALESVILLE BRANDFORT MARQUARD nodeAbove Average Combined Potential SOUTPAN VERKEERDEVLEI FICKSBURG High Combined Potential CLOCOLAN EXCELSIOR JACOBSDAL PETRUSBURG BLOEMFONTEIN THABA NCHU LADYBRAND LOCALITY PLAN TWEESPRUIT Economic BOTSHABELO THABA PATSHOA KOFFIEFONTEIN OPPERMANSDORP Power HOBHOUSE DEWETSDORP REDDERSBURG EDENBURG WEPENER LUCKHOFF FAURESMITH houses JAGERSFONTEIN VAN STADENSRUST TROMPSBURG SMITHFIELD DEPARTMENT LOCAL GOVERNMENT & HOUSING PHILIPPOLIS SPRINGFONTEIN Arid SPATIAL PLANNING DIRECTORATE ZASTRON SPATIAL INFORMATION SERVICES ROUXVILLE BETHULIE -

2021 BROCHURE the LONG LOOK the Pioneer Way of Doing Business
2021 BROCHURE THE LONG LOOK The Pioneer way of doing business We are an international company with a unique combination of cultures, languages and experiences. Our technologies and business environment have changed dramatically since Henry A. Wallace first founded the Hi-Bred Corn Company in 1926. This Long Look business philosophy – our attitude toward research, production and marketing, and the worldwide network of Pioneer employees – will always remain true to the four simple statements which have guided us since our early years: We strive to produce the best products in the market. We deal honestly and fairly with our employees, sales representatives, business associates, customers and stockholders. We aggressively market our products without misrepresentation. We provide helpful management information to assist customers in making optimum profits from our products. MADE TO GROW™ Farming is becoming increasingly more complex and the stakes ever higher. Managing a farm is one of the most challenging and critical businesses on earth. Each day, farmers have to make decisions and take risks that impact their immediate and future profitability and growth. For those who want to collaborate to push as hard as they can, we are strivers too. Drawing on our deep heritage of innovation and breadth of farming knowledge, we spark radical and transformative new thinking. And we bring everything you need — the high performing seed, the advanced technology and business services — to make these ideas reality. We are hungry for your success and ours. With us, you will be equipped to ride the wave of changing trends and extract all possible value from your farm — to grow now and for the future. -

The Youth Book. a Directory of South African Youth Organisations, Service Providers and Resource Material
DOCUMENT RESUME ED 432 485 SO 029 682 AUTHOR Barnard, David, Ed. TITLE The Youth Book. A Directory of South African Youth Organisations, Service Providers and Resource Material. INSTITUTION Human Sciences Research Council, Pretoria (South Africa). ISBN ISBN-0-7969-1824-4 PUB DATE 1997-04-00 NOTE 455p. AVAILABLE FROM Programme for Development Research, Human Sciences Research Council, P 0 Box 32410, 2017 Braamfontein, South Africa; Tel: 011-482-6150; Fax: 011-482-4739. PUB TYPE Reference Materials - Directories/Catalogs (132) EDRS PRICE MF01/PC19 Plus Postage. DESCRIPTORS Developing Nations; Educational Resources; Foreign Countries; Schools; Service Learning; *Youth; *Youth Agencies; *Youth Programs IDENTIFIERS Service Providers; *South Africa; Youth Service ABSTRACT With the goal of enhancing cooperation and interaction among youth, youth organizations, and other service providers to the youth sector, this directory aims to give youth, as well as people and organizations involved and interested in youth-related issues, a comprehensive source of information on South African youth organizations and related relevant issues. The directory is divided into three main parts. The first part, which is the background, is introductory comments by President Nelson Mandela and other officials. The second part consists of three directory sections, namely South African youth and children's organizations, South African educational institutions, including technical training colleges, technikons and universities, and South African and international youth organizations. The section on South African youth and children's organizations, the largest section, consists of 44 sectoral chapters, with each organization listed in a sectoral chapter representing its primary activity focus. Each organization is at the same time also cross-referenced with other relevant sectoral chapters, indicated by keywords at the bottom of an entry. -

FREE STATE DEPARTMENT of EDUCATION Address List: ABET Centres District: XHARIEP
FREE STATE DEPARTMENT OF EDUCATION Address List: ABET Centres District: XHARIEP Name of centre EMIS Category Hosting School Postal address Physical address Telephone Telephone number code number BA-AGI FS035000 PALC IKANYEGENG PO BOX 40 JACOBSDAL 8710 123 SEDITI STRE RATANANG JACOBSDAL 8710 053 5910112 GOLDEN FOUNTAIN FS018001 PALC ORANGE KRAG PRIMARY PO BOX 29 XHARIEP DAM 9922 ORANJEKRAG HYDROPARK LOCAT XHARIEP 9922 051-754 DAM IPOPENG FS029000 PALC BOARAMELO PO BOX 31 JAGERSFONTEIN 9974 965 ITUMELENG L JAGERSFORNTEIN 9974 051 7240304 KGOTHALLETSO FS026000 PALC ZASTRON PUBLIC PO BOX 115 ZASTRON 9950 447 MATLAKENG S MATLAKENG ZASTRPM 9950 051 6731394 LESEDI LA SETJABA FS020000 PALC EDENBURG PO BOX 54 EDENBURG 9908 1044 VELEKO STR HARASEBEI 9908 051 7431394 LETSHA LA FS112000 PALC TSHWARAGANANG PO BOX 56 FAURESMITH 9978 142 IPOPENG FAURESMITH 9978 051 7230197 TSHWARAGANANG MADIKGETLA FS023000 PALC MADIKGETLA PO BOX 85 TROMPSBURG 9913 392 BOYSEN STRE MADIKGETLA TROMPSBU 9913 051 7130300 RG MASIFUNDE FS128000 PALC P/BAG X1007 MASIFUNDE 9750 GOEDEMOED CORRE ALIWAL NORTH 9750 0 MATOPORONG FS024000 PALC ITEMELENG PO BOX 93 REDDERSBURG 9904 821 LESEDI STRE MATOPORONG 9904 051 5530726 MOFULATSHEPE FS021000 PALC MOFULATSHEPE PO BOX 237 SMITHFIELD 9966 474 JOHNS STREE MOFULATHEPE 9966 051 6831140 MPUMALANGA FS018000 PALC PHILIPPOLIS PO BOX 87 PHILIPPOLIS 9970 184 SCHOOL STRE PODING TSE ROLO PHILIPPOLIS 9970 051 7730220 REPHOLOHILE FS019000 PALC WONGALETHU PO BOX 211 BETHULIE 9992 JIM FOUCHE STR LEPHOI BETHULIE 9992 051 7630685 RETSWELELENG FS033000 PALC INOSENG PO BOX 216 PETRUSBURG 9932 NO 2 BOIKETLO BOIKETLO PETRUSBUR 9932 053 5740334 G THUTONG FS115000 PALC LUCKHOFF PO BOX 141 LUCKHOFF 9982 PHIL SAUNDERS A TEISVILLE LUCKHOFF 9982 053 2060115 TSIBOGANG FS030000 PALC LERETLHABETSE PO BOX 13 KOFFIEFONTEIN 9986 831 LEFAFA STRE DITLHAKE 9986 053 2050173 UBUNTU FS035001 PALS SAUNDERSHOOGTE P.O. -

Viljoenskroon Application Form Report 7Nov16.Pdf
Construction and strengthening of the 7 November 2016 Eskom infrastructure in the Revision: 0 Viljoenskroon area Reference: 111982 NEMA application form Eskom Document control record Document prepared by: Aurecon South Africa (Pty) Ltd Reg No 1977/003711/07 Aurecon Centre Lynnwood Bridge Office Park 4 Daventry Street Lynnwood Manor 0081 PO Box 74381 Lynnwood Ridge 0040 South Africa T +27 12 427 2000 F +27 86 556 0521 E [email protected] W aurecongroup.com A person using Aurecon documents or data accepts the risk of: a) Using the documents or data in electronic form without requesting and checking them for accuracy against the original hard copy version. b) Using the documents or data for any purpose not agreed to in writing by Aurecon. Document control Report title NEMA application form Document ID ViljoenskroonEIA/App Project number 111982 File path P:\Projects\111982 Viljoenskroon Sub Transmission BA\03 PRJ Del\6 REP\Application form\Viljoenskroon application form report_7Nov16.docx Client Eskom Client contact Earl Daniels Client reference 4502195620 (PO number) Rev Date Revision details/status Author Reviewer Verifier Approver (if required) 0 7 November 2016 Application form C Durr N BHJ Smit Whitehorn Current revision 0 Approval Author signature Approver signature Name Candice Dürr Name Barend Smit Title Environmental Scientist Title Technical Director Project 111982 File Viljoenskroon application form report_7Nov16.docx 7 November 2016 Revision 0 Construction and strengthening of the Eskom infrastructure in the Viljoenskroon area Date 7 November 2016 Reference 111982 Revision 0 Aurecon South Africa (Pty) Ltd Reg No 1977/003711/07 Aurecon Centre Lynnwood Bridge Office Park 4 Daventry Street Lynnwood Manor 0081 PO Box 74381 Lynnwood Ridge 0040 South Africa T +27 12 427 2000 F +27 86 556 0521 E [email protected] W aurecongroup.com Project 111982 File Viljoenskroon application form report_7Nov16.docx 7 November 2016 Revision 0 Contents 1. -

Free State Province
Agri-Hubs Identified by the Province FREE STATE PROVINCE 27 PRIORITY DISTRICTS PROVINCE DISTRICT MUNICIPALITY PROPOSED AGRI-HUB Free State Xhariep Springfontein 17 Districts PROVINCE DISTRICT MUNICIPALITY PROPOSED AGRI-HUB Free State Thabo Mofutsanyane Tshiame (Harrismith) Lejweleputswa Wesselsbron Fezile Dabi Parys Mangaung Thaba Nchu 1 SECTION 1: 27 PRIORITY DISTRICTS FREE STATE PROVINCE Xhariep District Municipality Proposed Agri-Hub: Springfontein District Context Demographics The XDM covers the largest area in the FSP, yet has the lowest Xhariep has an estimated population of approximately 146 259 people. population, making it the least densely populated district in the Its population size has grown with a lesser average of 2.21% per province. It borders Motheo District Municipality (Mangaung and annum since 1996, compared to that of province (2.6%). The district Naledi Local Municipalities) and Lejweleputswa District Municipality has a fairly even population distribution with most people (41%) (Tokologo) to the north, Letsotho to the east and the Eastern Cape residing in Kopanong whilst Letsemeng and Mohokare accommodate and Northern Cape to the south and west respectively. The DM only 32% and 27% of the total population, respectively. The majority comprises three LMs: Letsemeng, Kopanong and Mohokare. Total of people living in Xhariep (almost 69%) are young and not many Area: 37 674km². Xhariep District Municipality is a Category C changes have been experienced in the age distribution of the region municipality situated in the southern part of the Free State. It is since 1996. Only 5% of the total population is elderly people. The currently made up of four local municipalities: Letsemeng, Kopanong, gender composition has also shown very little change since 1996, with Mohokare and Naledi, which include 21 towns. -
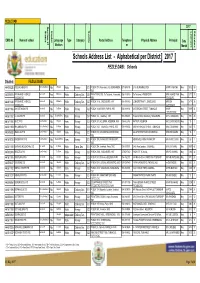
Fezile Dabi Address List 31 May 2017.Pdf
FEZILE DABI Section 21 2017 Quintile Hostel Status Educators Learners EMIS Nr. Name of school Language Type Category Postal Address Telephone Physical Address Principal Data Medium nr. Month Schools Address List - Alphabetical per District 2017 FEZILE DABI: Schools District: FEZILE DABI 444306220 ADELINE MEJE P/S Partly Section 21 No English Public Primary Q1 PO BOX 701, Rammulotsi, VILJOENSKROON, 071-9698718 2181 JS, RAMMULUTSI Mr FP THABATHA May 1012 30 9520 442506316 AFRIKAANSE H/SKOOL Section 21 Yes Afrikaans Public Ordinary Sec. Q5 PRIVATE BAG X53, Du Toitstraat , Kroonstad, 056-2123159 Du Toitstraat , KROONSTAD MNR A JANSE VAN May 377 25 KROONSTAD 9500 RENSBURG 443611240 AFRIKAANSE H/SKOOL Section 21 No Afrikaans Public Ordinary Sec. Q5 PO BOX 1116, , SASOLBURG, 1947 016-9761060 LEMMERSTRAAT 1, SASOLBURG MNR DH May 673 36 SASOLBURG KLEYNHANS 443011166 AHA SETJHABA P/S Section 21 No SeSotho Public Primary Q2 PO BOX 1126, PARYS, PARYS, 9585 056-8198192 4955 BROWN STREET, TUMAHOLE Mr MP May 1095 34 LETLOENYANE 443611252 AJ JACOBS P/S Section 21 No Dual: Afr/Eng Public Primary Q4 PO BOX 112, , Sasolburg, 1947 016-9762000 Wepener Street Sasolburg, SASOLBURG Mr H.J. MOOLMAN May 595 29 441811160 ALICE PF/S Non-Section 21 No English Farm Primary Q1 PO BOX 251, HEILBRON, HEILBRON, 9650 05885-22782 KATKOP, HEILBRON Ms E.D MOFOKENG May 15 1 443011183 AM LEMBEDE P/S Partly Section 21 No SeSotho Public Primary Q3 PO BOX 1123, TUMAHOLE, PARYS, 9585 056-8198054 2028 MTHIMKULU STREET, TUMAHOLE Miss O.D MARAKE May 340 13 442506122 AMACILIA PF/S Non-Section 21 No English Farm Primary Q1 PO BOX 676, KROONSTAD, KROONSTAD, - KALKFONTEIN FARM, KROONSTAD MISS ED DLAMINI May 18 1 9500 441610010 ANDERKANT PF/S Non-Section 21 No Dual: Afr/Eng Farm Primary Q1 PO BOX 199, FRANKFORT, FRANKFORT, - MERRIVALE FARM, FRANKFORT Mrs A MOTLOUNG May 26 1 9830 443011135 BARNARD MOLOKOANE S/S Section 21 No SeSotho Public Comp. -

44067 15-01 Legal B
Government Gazette Staatskoerant REPUBLIC OF SOUTH AFRICA REPUBLIEK VAN SUID-AFRIKA January Vol. 667 Pretoria, 15 2021 Januarie No. 44067 PART 1 OF 2 B LEGAL NOTICES WETLIKE KENNISGEWINGS SALES IN EXECUTION AND OTHER PUBLIC SALES GEREGTELIKE EN ANDER OPENBARE VERKOPE ISSN 1682-5843 N.B. The Government Printing Works will 44067 not be held responsible for the quality of “Hard Copies” or “Electronic Files” submitted for publication purposes 9 771682 584003 AIDS HELPLINE: 0800-0123-22 Prevention is the cure 2 No. 44067 GOVERNMENT GAZETTE, 15 JANUARY 2021 IMPORTANT NOTICE OF OFFICE RELOCATION Private Bag X85, PRETORIA, 0001 149 Bosman Street, PRETORIA Tel: 012 748 6197, Website: www.gpwonline.co.za URGENT NOTICE TO OUR VALUED CUSTOMERS: PUBLICATIONS OFFICE’S RELOCATION HAS BEEN TEMPORARILY SUSPENDED. Please be advised that the GPW Publications office will no longer move to 88 Visagie Street as indicated in the previous notices. The move has been suspended due to the fact that the new building in 88 Visagie Street is not ready for occupation yet. We will later on issue another notice informing you of the new date of relocation. We are doing everything possible to ensure that our service to you is not disrupted. As things stand, we will continue providing you with our normal service from the current location at 196 Paul Kruger Street, Masada building. Customers who seek further information and or have any questions or concerns are free to contact us through telephone 012 748 6066 or email Ms Maureen Toka at [email protected] or cell phone at 082 859 4910. -

Pnads295.Pdf
TABLE OF CONTENTS Letter from the Honourable Premier of the Free State 3 Provincial Map, Free State 4 How to use the HIV-911 directory 6 SEARCH BY DISTRICT MUNICIPALITY DC20 Fezile Dabi 9 DC18 Lejweleputswa 15 DC17 Motheo 21 DC19 Thabo Mofutsanyane 31 DC16 Xhariep 39 Acknowledgements 43 Order form 44 Organisational Update Form - Update your organisational details 45 “This directory of HIV-related services in Free State is partially made possible by the generous support of the American people through the United States Agency for International Development (USAID) and the President’s Emergency Plan.The contents are the responsibility of the Centre for HIV/AIDS Networking (through a Sub-Agreement with Foundation for Professional Development) and do not necessarily reflect the views of USAID or the United States Government” 1 HOW TO USE THE HIV-911 DIRECTORY WHO IS THE DIRECTORY FOR? This directory is for anyone who is seeking information on where to locate HIV/AIDS services and support in Free State. WHAT INFORMATION DOES THE DIRECTORY CONTAIN? Within the directory you will find information on organisations that provide HIV/AIDS-related services and support in each municipality within Free State. We have provided full contact details, an organisational overview and a listing of services for each organisation. Details on a range of HIV-related services are provided, from government clinics that dispense anti-retro- viral drugs (ARVs) and provide Voluntary Counselling and Testing (VCT), to faith-based and non-governmental interventions and Community Home-based Care and food parcel support programmes. HOW DO I USE THE DIRECTORY? There are close to 200 organisations working in HIV/AIDS in Free State.