DOCSLIB.ORG

The Linkedin Hack: Understanding Why It Was So Easy to Crack the Passwords

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Linkedin Hack: Understanding Why It Was So Easy to Crack the Passwords The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords LinkedIn was breached in 2012 with a reported 6.5 million user accounts compromised. LinkedIn sent a request to known hacked users advising them to change their passwords. However, on May 16, 2016, 117 million LinkedIn accounts–reportedly from the 2012 hack–were found to be up for sale on a hacker site. LinkedIn stated that after the initial 2012 breach, they added enhanced protection, most likely adding the “salt” functionality to their passwords. However, if you have not changed your password since 2012, you do not have the added protection of a salted password hash. You may be asking yourself–what on earth are hashing and salting and how does this all work? By Tyler Cohen Wood The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood When creating a site that collects and stores user accounts, it is critical to ensure that passwords are properly protected. Because there are so many ways to crack passwords, including guessing (typically by using social media to figure out birthdays, pets’ names, favorite sports teams, etc.), dictionary attacks, and the use of rainbow tables (which we’ll go into later), it is more vital than ever to employ unique salted password hashing, which is in compliance with current cybersecurity industry standards. First, let’s understand how this all works. When a user first creates an account, they enter a password in plain text, such as “1234.” The password “1234” is then hashed and stored in the system. Hashing is a mathematical algorithm that takes a plain text password and turns it into a set of letters and numbers. There are several methods of hashing. One method is called Secure Hash Algorithm 1 (SHA1) (which is what LinkedIn had reportedly been using at the time of the 2012 hack) where, a plain text password runs through a mathematical cryptographic algorithm, which turns and stores the text password (“1234”) into a set of numbers and letters that look like this: sha1: 7110eda4d09e062aa5e4a390b0a572ac0d2c0220 Therefore, the password should never be stored in the database as plain text, but rather as a stored hash. When a user logs into their account by entering their text password “1234,” the hash of the password is checked against the stored hash of the password. If the hashes match, the user is allowed access. If the hash does not match, the user will not be able to gain access. When using the SHA1 method, without adding the salt, the plain text password of “1234” will always create the same hash, meaning “1234” will always hash to the following SHA1 hash value: 7110eda4d09e062aa5e4a390b0a572ac0d2c0220 1 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood In theory, a hacker who has stolen user accounts that use the SHA1 mathematical algorithm with non-salted hashed passwords should not be able to use the hash to get the original text password. However, the bad news is that there are ways to reconstruct the text string from the hash. If a hacker has access to a database that has a SHA1 hash dictionary that has already been converted into the password plain text string it equals, they will have easy access to the password. It would look something like this: Plain Text Password SHA1 Hash String 1234 7110eda4d09e062aa5e4a390b0a572ac0d2c0220 Password 8be3c943b1609fffbfc51aad666d0a04adf83c9d Tyler c794bd35db97c1cf0b8edc21ac218cd202f68ca7 Myd0gH0rat10 424f6b34ac904e1d8feb8dd96338df4fad2e67f8 Figure 1 If the hacker cannot succeed in cracking passwords through brute force or by guessing the passwords, there are other methods that can be used, such as lookup tables and rainbow tables. Lookup tables provide hashes that have already been computed and stored in a password dictionary with their corresponding plain text password string such as the ones listed in Figure 1 above. 2 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood Rainbow tables are lists of known hash values that equal a plain text password, somewhat like Figure 1 above. Rainbow tables work in a similar manner to Lookup tables with a few minor differences—mainly that they sacrifice hash cracking speed to reduce the size of lookup tables. What is important to take away is that both lookup tables and rainbow tables have databases of plain text passwords and the exact hash string that matches each password. The reason lookup tables and rainbow tables work is because each password has been hashed exactly the same way. This means that if SHA1 has been used and two people have the password “1234,” the password hash will be identical. If I go to a website such as http://sha1.gromweb.com/ which uses an SHA1 dictionary that has many pre-converted hashes, I can find the password I’m looking for: SHA-1 conversion and SHA-1 reverse lookup Reverse a SHA-1 hash Enter a SHA-1 hash to reverse... Reverse 3 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood Next, I will enter the hash from the password “1234”: SHA-1 conversion and SHA-1 reverse lookup Reverse a SHA-1 hash 1234| X Reverse After clicking the reverse button, I come up with the hash string: SHA-1 conversion and SHA-1 reverse lookup Reverse a SHA-1 hash 7110eda4d09e062aa5e4a390b0a572ac0d2c0220 Reverse 4 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood You can also choose to reverse the hash value to get the password text string as shown below: SHA-1 reverse for 7110eda4d09e062aa5e4a390b0a572ac0d2c0220 The SHA-1 hash: 7110eda4d09e062aa5e4a390b0a572ac0d2c0220 was successfully reversed into the string: 1234 It is really that simple. I was able to get the password by simply taking a millisecond to retrieve the password from a website. Kind of scary. So what can we do? This is where salts comes in. This type of hack can be prevented by employing a unique salt that will make each plain text password converted to hash different. This way no two identical passwords will have the same hash. A salt is a unique string of bytes that is included with the password in each hash calculation. If done properly, salts make lookup tables and rainbow tables ineffective (at least at the present time). However, it is important to use salts correctly. It is crucial to use a unique salt every time a user and account/password is created and when a user changes their password. In other words, never use the same salt for each password and hash. 5 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood Here’s a great depiction of how the password “foobar” without a salt will always hash to the same hash string: Without Salting encrypt foobar fgjhdfuyre8 encrypt foobar fgjhdfuyre8 Here’s the salting process and how the password “foobar” now has a unique hash string: With Salt add salt encrypt foobar 1AUW foobar uyfieeiruoe add salt encrypt foobar eB46 foobar fgijhdkjghryt So if both users, John and Sean, have the same SHA1 plain text password string “1234,” we have established that without a unique salt, the hash will be the same. Figures on page 6: http://weblogs.asp.net/jcogley/symmetric-salting-remember-that-salt-goes-with-more-than-just-hash 6 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood Remember, without a salt, the hash for the password “1234” will be hashed to identical hash strings: John:7110eda4d09e062aa5e4a390b0a572ac0d2c0220 Sean:7110eda4d09e062aa5e4a390b0a572ac0d2c0220 However, by adding a unique salt each time, the hash will be different. This is a simplified example, but by going to a site like http://online-code- generator.com/sha1-hash-with-optional-salt.php, which allows you to create hashes with or without salts based on a plain text password, you can see that the hashes are different. From this site, I chose to use the password “1234” and a salt string of characters before the string: SHA1 Hash Generator With this online generator, you can calculate the SHA1 hash of a string with an optional salt value. MD5 is a hash type that follows the RFC 3174 - US Secure Hash Algorithm 1 1234 add a salt before this string. pepper generate sha1 hash 7 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood Notice how the hash is now different for the password “1234” than it was without the salt added: SHA1 Hash Generator Result: 84b3f681fc75231dbc31a7c5103f9d4fd8f91615 However, remember to always use a different salt each time. In the next example, I again used the password string “1234” and the same salt string and once again put the salt before the string: SHA1 Hash Generator With this online generator, you can calculate the SHA1 hash of a string with an optional salt value. MD5 is a hash type that follows the RFC 3174 - US Secure Hash Algorithm 1 1234 add a salt before this string. pepper generate sha1 hash 8 © 2016, Inspired eLearning, LLC. All Rights Reserved. The LinkedIn Hack: Understanding Why It Was So Easy to Crack the Passwords Tyler Cohen Wood Notice the hash string is exactly the same as the prior example. This is because I used the same text string with the same salt in the same location: SHA1 Hash Generator Result: 84b3f681fc75231dbc31a7c5103f9d4fd8f91615 Now, what if I use the same text password and choose to use a different salt string of characters? Will this make the hash string different and unique? Let’s see below: SHA1 Hash Generator With this online generator, you can calculate the SHA1 hash of a string with an optional salt value.
Load more

Recommended publications
  • Argon and Argon2
    Argon and Argon2 Designers: Alex Biryukov, Daniel Dinu, and Dmitry Khovratovich University of Luxembourg, Luxembourg [email protected], [email protected], [email protected] https://www.cryptolux.org/index.php/Password https://github.com/khovratovich/Argon https://github.com/khovratovich/Argon2 Version 1.1 of Argon Version 1.0 of Argon2 31th January, 2015 Contents 1 Introduction 3 2 Argon 5 2.1 Specification . 5 2.1.1 Input . 5 2.1.2 SubGroups . 6 2.1.3 ShuffleSlices . 7 2.2 Recommended parameters . 8 2.3 Security claims . 8 2.4 Features . 9 2.4.1 Main features . 9 2.4.2 Server relief . 10 2.4.3 Client-independent update . 10 2.4.4 Possible future extensions . 10 2.5 Security analysis . 10 2.5.1 Avalanche properties . 10 2.5.2 Invariants . 11 2.5.3 Collision and preimage attacks . 11 2.5.4 Tradeoff attacks . 11 2.6 Design rationale . 14 2.6.1 SubGroups . 14 2.6.2 ShuffleSlices . 16 2.6.3 Permutation ...................................... 16 2.6.4 No weakness,F no patents . 16 2.7 Tweaks . 17 2.8 Efficiency analysis . 17 2.8.1 Modern x86/x64 architecture . 17 2.8.2 Older CPU . 17 2.8.3 Other architectures . 17 3 Argon2 19 3.1 Specification . 19 3.1.1 Inputs . 19 3.1.2 Operation . 20 3.1.3 Indexing . 20 3.1.4 Compression function G ................................. 21 3.2 Features . 22 3.2.1 Available features . 22 3.2.2 Server relief . 23 3.2.3 Client-independent update .
    [Show full text]
  • CASH: a Cost Asymmetric Secure Hash Algorithm for Optimal Password Protection
    CASH: A Cost Asymmetric Secure Hash Algorithm for Optimal Password Protection Jeremiah Blocki Anupam Datta Microsoft Research Carnegie Mellon University August 23, 2018 Abstract An adversary who has obtained the cryptographic hash of a user's password can mount an offline attack to crack the password by comparing this hash value with the cryptographic hashes of likely password guesses. This offline attacker is limited only by the resources he is willing to invest to crack the password. Key-stretching techniques like hash iteration and memory hard functions have been proposed to mitigate the threat of offline attacks by making each password guess more expensive for the adversary to verify. However, these techniques also increase costs for a legitimate authentication server. We introduce a novel Stackelberg game model which captures the essential elements of this interaction between a defender and an offline attacker. In the game the defender first commits to a key-stretching mechanism, and the offline attacker responds in a manner that optimizes his utility (expected reward minus expected guessing costs). We then introduce Cost Asymmetric Secure Hash (CASH), a randomized key-stretching mechanism that minimizes the fraction of passwords that would be cracked by a rational offline attacker without increasing amortized authentication costs for the legitimate authentication server. CASH is motivated by the observation that the legitimate authentication server will typically run the authentication procedure to verify a correct password, while an offline adversary will typically use incorrect password guesses. By using randomization we can ensure that the amortized cost of running CASH to verify a correct password guess is significantly smaller than the cost of rejecting an incorrect password.
    [Show full text]
  • Intro to Cryptography 1 Introduction 2 Secure Password Manager
    Programming Assignment 1 Winter 2021 CS 255: Intro to Cryptography Prof. Dan Boneh Due Monday, Feb. 8, 11:59pm 1 Introduction In many software systems today, the primary weakness often lies in the user’s password. This is especially apparent in light of recent security breaches that have highlighted some of the weak passwords people commonly use (e.g., 123456 or password). It is very important, then, that users choose strong passwords (or “passphrases”) to secure their accounts, but strong passwords can be long and unwieldy. Even more problematic, the user generally has many different services that use password authentication, and as a result, the user has to recall many different passwords. One way for users to address this problem is to use a password manager, such as LastPass and KeePass. Password managers make it very convenient for users to use a unique, strong password for each service that requires password authentication. However, given the sensitivity of the data contained in the password manager, it takes considerable care to store the information securely. In this assignment, you will be writing a secure and efficient password manager. In your implemen- tation, you will make use of various cryptographic primitives we have discussed in class—notably, authenticated encryption and collision-resistant hash functions. Because it is ill-advised to imple- ment your own primitives in cryptography, you should use an established library: in this case, the Stanford Javascript Crypto Library (SJCL). We will provide starter code that contains a basic tem- plate, which you will be able to fill in to satisfy the functionality and security properties described below.
    [Show full text]
  • User Authentication and Cryptographic Primitives
    User Authentication and Cryptographic Primitives Brad Karp UCL Computer Science CS GZ03 / M030 16th November 2016 Outline • Authenticating users – Local users: hashed passwords – Remote users: s/key – Unexpected covert channel: the Tenex password- guessing attack • Symmetric-key-cryptography • Public-key cryptography usage model • RSA algorithm for public-key cryptography – Number theory background – Algorithm definition 2 Dictionary Attack on Hashed Password Databases • Suppose hacker obtains copy of password file (until recently, world-readable on UNIX) • Compute H(x) for 50K common words • String compare resulting hashed words against passwords in file • Learn all users’ passwords that are common English words after only 50K computations of H(x)! • Same hashed dictionary works on all password files in world! 3 Salted Password Hashes • Generate a random string of bytes, r • For user password x, store [H(r,x), r] in password file • Result: same password produces different result on every machine – So must see password file before can hash dictionary – …and single hashed dictionary won’t work for multiple hosts • Modern UNIX: password hashes salted; hashed password database readable only by root 4 Salted Password Hashes • Generate a random string of bytes, r Dictionary• For user password attack still x, store possible [H(r,x after), r] in attacker seespassword password file file! Users• Result: should same pick password passwords produces that different aren’t result close to ondictionary every machine words. – So must see password file
    [Show full text]
  • To Change Your Ud Password(S)
    TO CHANGE YOUR UD PASSWORD(S) The MyCampus portal allows the user a single-signon for campus applications. IMPORTANT NOTICE AT BOTTOM OF THESE INSTRUCTIONS !! INITIAL PROCEDURE TO ALLOW YOU TO CHANGE YOUR PASSWORD ON THE UD NETWORK : 1. In your web browser, enter http://mycampus.dbq.edu . If you are logging in for the first time, you will be directed to answer (3) security questions. Also, be sure to answer one of the recovery methods. 2. Once the questions are answered, you will click on SUBMIT and then CONTINUE and then YES. 3. In one location, you will now find MyUD, Campus Portal, Email and UDOnline (Moodle). 4. You can now click on any of these apps and you will be logged in already. The email link will prompt you for the password a second time until we get all accounts set up properly. YOU MUST BE SURE TO LOGOUT OF EACH APPLICATION AFTER YOU’RE DONE USING IT !! TO CHANGE YOUR PASSWORD: 1. After you have logged into the MyCampus.dbq.edu website, you will see your username in the upper- right corner of the screen. 2. Click on your name and then go into My Account. 3. At the bottom, you will click on Change Password and then proceed as directed. 4. You can now logout. You will need to use your new password on your next login. Password must be a minimum of 6 characters and contain 3 of the following 4 categories: - Uppercase character - Lowercase character - Number - Special character You cannot use the previous password You’ll be required to change your password every 180 days.
    [Show full text]
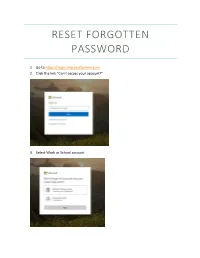
  • Reset Forgotten Password with Office365
    RESET FORGOTTEN PASSWORD 1. Go to https://login.microsoftonline.com 2. Click the link “Can’t access your account?” 3. Select Work or School account 4. Enter in your User ID with the @uamont.edu at the end and then enter the characters as seen in the picture. You can click the refresh button for a different set of letters. 5. You will have 3 options to verify your account and reset your password. This information was set up when you registered with self-service password reset. If you have not registered, please go to https://aka.ms/ssprsetup and enter in your information. A step by step guide on how to do this can be found here. a. Text your mobile phone b. Call your mobile phone c. Answer Security Questions 6. Choose one option and enter the information requested 7. Click Text for text my mobile phone, Call for call my mobile phone, or click Next when you’ve answered all security questions. a. If you have selected Text my mobile phone you will be required to enter in a verification code and click Next b. If you have select Call my mobile phone you will receive a call and will need to enter # to verify. 8. Enter in your new password and click Finish a. Note: If you receive the message, “Unfortunately, your password contains a word, phrase, or pattern that makes it easily guessable. Please try again with a different password.” Please try to create a password that does not use any dictionary words. b. Passwords must meet 3 of the 4 following requirements i.
    [Show full text]
  • Optimizing a Password Hashing Function with Hardware-Accelerated Symmetric Encryption
    S S symmetry Article Optimizing a Password Hashing Function with Hardware-Accelerated Symmetric Encryption Rafael Álvarez 1,* , Alicia Andrade 2 and Antonio Zamora 3 1 Departamento de Ciencia de la Computación e Inteligencia Artificial (DCCIA), Universidad de Alicante, 03690 Alicante, Spain 2 Fac. Ingeniería, Ciencias Físicas y Matemática, Universidad Central, Quito 170129, Ecuador; [email protected] 3 Departamento de Ciencia de la Computación e Inteligencia Artificial (DCCIA), Universidad de Alicante, 03690 Alicante, Spain; [email protected] * Correspondence: [email protected] Received: 2 November 2018; Accepted: 22 November 2018; Published: 3 December 2018 Abstract: Password-based key derivation functions (PBKDFs) are commonly used to transform user passwords into keys for symmetric encryption, as well as for user authentication, password hashing, and preventing attacks based on custom hardware. We propose two optimized alternatives that enhance the performance of a previously published PBKDF. This design is based on (1) employing a symmetric cipher, the Advanced Encryption Standard (AES), as a pseudo-random generator and (2) taking advantage of the support for the hardware acceleration for AES that is available on many common platforms in order to mitigate common attacks to password-based user authentication systems. We also analyze their security characteristics, establishing that they are equivalent to the security of the core primitive (AES), and we compare their performance with well-known PBKDF algorithms, such as Scrypt and Argon2, with favorable results. Keywords: symmetric; encryption; password; hash; cryptography; PBKDF 1. Introduction Key derivation functions are employed to obtain one or more keys from a master secret. This is especially useful in the case of user passwords, which can be of arbitrary length and are unsuitable to be used directly as fixed-size cipher keys, so, there must be a process for converting passwords into secret keys.
    [Show full text]
  • Rifflescrambler – a Memory-Hard Password Storing Function ⋆
    RiffleScrambler – a memory-hard password storing function ? Karol Gotfryd1, Paweł Lorek2, and Filip Zagórski1;3 1 Wrocław University of Science and Technology Faculty of Fundamental Problems of Technology Department of Computer Science 2 Wrocław University Faculty of Mathematics and Computer Science Mathematical Institute 3 Oktawave Abstract. We introduce RiffleScrambler: a new family of directed acyclic graphs and a corresponding data-independent memory hard function with password independent memory access. We prove its memory hard- ness in the random oracle model. RiffleScrambler is similar to Catena – updates of hashes are determined by a graph (bit-reversal or double-butterfly graph in Catena). The ad- vantage of the RiffleScrambler over Catena is that the underlying graphs are not predefined but are generated per salt, as in Balloon Hashing. Such an approach leads to higher immunity against practical parallel at- tacks. RiffleScrambler offers better efficiency than Balloon Hashing since the in-degree of the underlying graph is equal to 3 (and is much smaller than in Ballon Hashing). At the same time, because the underlying graph is an instance of a Superconcentrator, our construction achieves the same time-memory trade-offs. Keywords: Memory hardness, password storing, Markov chains, mixing time. 1 Introduction In early days of computers’ era passwords were stored in plaintext in the form of pairs (user; password). Back in 1960s it was observed, that it is not secure. It took around a decade to incorporate a more secure way of storing users’ passwords – via a DES-based function crypt, as (user; fk(password)) for a se- cret key k or as (user; f(password)) for a one-way function.
    [Show full text]
  • Strong Password-Based Authentication in TLS Using the Three-Party Group Diffie–Hellman Protocol
    284 Int. J. Security and Networks, Vol. 2, Nos. 3/4, 2007 Strong password-based authentication in TLS using the three-party group Diffie–Hellman protocol Michel Abdalla* École normale supérieure – CNRS, LIENS, Paris, France E-mail: [email protected] *Corresponding author Emmanuel Bresson Department of Cryptology, CELAR Technology Center, Bruz, France E-mail: [email protected] Olivier Chevassut Lawrence Berkeley National Laboratory, Berkeley, CA, USA E-mail: [email protected] Bodo Möller Horst Görtz Institute for IT Security, Ruhr-Universität Bochum, Bochum, Germany E-mail: [email protected] David Pointcheval École normale supérieure – CNRS, LIENS, Paris, France E-mail: [email protected] Abstract: The internet has evolved into a very hostile ecosystem where ‘phishing’ attacks are common practice. This paper shows that the three-party group Diffie-Hellman key exchange can help protect against these attacks. We have developed password-based ciphersuites for the Transport Layer Security (TLS) protocol that are not only provably secure but also believed to be free from patent and licensing restrictions based on an analysis of relevant patents in the area. Keywords: password authentication; group Diffie–Hellman key exchange; transport layer security; TLS. Reference to this paper should be made as follows: Abdalla, M., Bresson, E., Chevassut, O., Möller, B. and Pointcheval, D. (2007) ‘Strong password-based authentication in TLS using the three-party group Diffie-Hellman protocol’, Int. J. Security and Networks, Vol. 2, Nos. 3/4, pp.284–296. Biographical notes: Michel Abdalla is currently a Researcher with the Centre National de la Recherche Scientifique (CNRS), France and a Member of the Cryptography Team at the Ecole Normale Supérieure (ENS), France.
    [Show full text]
  • Hash Functions
    11 Hash Functions Suppose you share a huge le with a friend, but you are not sure whether you both have the same version of the le. You could send your version of the le to your friend and they could compare to their version. Is there any way to check that involves less communication than this? Let’s call your version of the le x (a string) and your friend’s version y. The goal is to determine whether x = y. A natural approach is to agree on some deterministic function H, compute H¹xº, and send it to your friend. Your friend can compute H¹yº and, since H is deterministic, compare the result to your H¹xº. In order for this method to be fool-proof, we need H to have the property that dierent inputs always map to dierent outputs — in other words, H must be injective (1-to-1). Unfortunately, if H is injective and H : f0; 1gin ! f0; 1gout is injective, then out > in. This means that sending H¹xº is no better/shorter than sending x itself! Let us call a pair ¹x;yº a collision in H if x , y and H¹xº = H¹yº. An injective function has no collisions. One common theme in cryptography is that you don’t always need something to be impossible; it’s often enough for that thing to be just highly unlikely. Instead of saying that H should have no collisions, what if we just say that collisions should be hard (for polynomial-time algorithms) to nd? An H with this property will probably be good enough for anything we care about.
    [Show full text]
  • Cs 255 (Introduction to Cryptography)
    CS 255 (INTRODUCTION TO CRYPTOGRAPHY) DAVID WU Abstract. Notes taken in Professor Boneh’s Introduction to Cryptography course (CS 255) in Winter, 2012. There may be errors! Be warned! Contents 1. 1/11: Introduction and Stream Ciphers 2 1.1. Introduction 2 1.2. History of Cryptography 3 1.3. Stream Ciphers 4 1.4. Pseudorandom Generators (PRGs) 5 1.5. Attacks on Stream Ciphers and OTP 6 1.6. Stream Ciphers in Practice 6 2. 1/18: PRGs and Semantic Security 7 2.1. Secure PRGs 7 2.2. Semantic Security 8 2.3. Generating Random Bits in Practice 9 2.4. Block Ciphers 9 3. 1/23: Block Ciphers 9 3.1. Pseudorandom Functions (PRF) 9 3.2. Data Encryption Standard (DES) 10 3.3. Advanced Encryption Standard (AES) 12 3.4. Exhaustive Search Attacks 12 3.5. More Attacks on Block Ciphers 13 3.6. Block Cipher Modes of Operation 13 4. 1/25: Message Integrity 15 4.1. Message Integrity 15 5. 1/27: Proofs in Cryptography 17 5.1. Time/Space Tradeoff 17 5.2. Proofs in Cryptography 17 6. 1/30: MAC Functions 18 6.1. Message Integrity 18 6.2. MAC Padding 18 6.3. Parallel MAC (PMAC) 19 6.4. One-time MAC 20 6.5. Collision Resistance 21 7. 2/1: Collision Resistance 21 7.1. Collision Resistant Hash Functions 21 7.2. Construction of Collision Resistant Hash Functions 22 7.3. Provably Secure Compression Functions 23 8. 2/6: HMAC And Timing Attacks 23 8.1. HMAC 23 8.2.
    [Show full text]
  • Password Cracking
    Password Cracking Sam Martin and Mark Tokutomi 1 Introduction Passwords are a system designed to provide authentication. There are many different ways to authenticate users of a system: a user can present a physical object like a key card, prove identity using a personal characteristic like a fingerprint, or use something that only the user knows. In contrast to the other approaches listed, a primary benefit of using authentication through a pass- word is that in the event that your password becomes compromised it can be easily changed. This paper will discuss what password cracking is, techniques for password cracking when an attacker has the ability to attempt to log in to the system using a user name and password pair, techniques for when an attacker has access to however passwords are stored on the system, attacks involve observing password entry in some way and finally how graphical passwords and graphical password cracks work. Figure 1: The flow of password attacking possibilities. Figure 1 shows some scenarios attempts at password cracking can occur. The attacker can gain access to a machine through physical or remote access. The user could attempt to try each possible password or likely password (a form of dictionary attack). If the attack can gain access to hashes of the passwords it is possible to use software like OphCrack which utilizes Rainbow Tables to crack passwords[1]. A spammer may use dictionary attacks to gain access to bank accounts or other 1 web services as well. Wireless protocols are vulnerable to some password cracking techniques when packet sniffers are able to gain initialization packets.
    [Show full text]