Apple Tree System Research
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

APPLE (Fruit Varieties)
E TG/14/9 ORIGINAL: English DATE: 2005-04-06 INTERNATIONAL UNION FOR THE PROTECTION OF NEW VARIETIES OF PLANTS GENEVA * APPLE (Fruit Varieties) UPOV Code: MALUS_DOM (Malus domestica Borkh.) GUIDELINES FOR THE CONDUCT OF TESTS FOR DISTINCTNESS, UNIFORMITY AND STABILITY Alternative Names:* Botanical name English French German Spanish Malus domestica Apple Pommier Apfel Manzano Borkh. The purpose of these guidelines (“Test Guidelines”) is to elaborate the principles contained in the General Introduction (document TG/1/3), and its associated TGP documents, into detailed practical guidance for the harmonized examination of distinctness, uniformity and stability (DUS) and, in particular, to identify appropriate characteristics for the examination of DUS and production of harmonized variety descriptions. ASSOCIATED DOCUMENTS These Test Guidelines should be read in conjunction with the General Introduction and its associated TGP documents. Other associated UPOV documents: TG/163/3 Apple Rootstocks TG/192/1 Ornamental Apple * These names were correct at the time of the introduction of these Test Guidelines but may be revised or updated. [Readers are advised to consult the UPOV Code, which can be found on the UPOV Website (www.upov.int), for the latest information.] i:\orgupov\shared\tg\applefru\tg 14 9 e.doc TG/14/9 Apple, 2005-04-06 - 2 - TABLE OF CONTENTS PAGE 1. SUBJECT OF THESE TEST GUIDELINES..................................................................................................3 2. MATERIAL REQUIRED ...............................................................................................................................3 -

2019 Newsletter
Front page: Allen’s greeting, something new 2019 NEWSLETTER A Message From Our President & Owner, EVENT CALENDAR Cooler mornings and valley fog below the orchard remind us all that it’s about apple time! Nature has blessed us with August 19th a beautiful crop of apples with exceptionally good fruit size. Opening Day Compared to recent years, some varieties may be picked a little later this year so be sure to give us a call or check our website to September 27th - 29th make sure your favorite apple is available. I enjoy every apple Gays Mills Apple Festival variety we grow, but Evercrisp has me as excited as Honeycrisp. October 5th - 6th Harvested in late October and stored in a refrigerator, Evercrisp Sunrise Samples Weekend is a fantastic eating experience in the winter months. Our family has been growing apples since 1934 and we have never tasted October 12th - 13th another winter apple like Evercrisp! Family Fun Weekend I hope you all enjoyed our newly expanded sales area and October 19th - 20th bathrooms added in 2018. This year we have made additional Harvest Celebration exciting improvements with a new gift area, live apple packing & Helicopter Rides TV, and a working model train for young and old to enjoy. Our famous cider donuts will be back- made fresh every day. Please (weather permitting ) enjoy our free apple and cider samples along with many of the October 21st - December 16th other products we sell. Gift Box Shipping Begins Don’t forget our online store. We feature many of the October 26th - 27th items available here and have made it far easier to order gift pack Trick or Treat Weekend apples this year from home. -

Variety Description Origin Approximate Ripening Uses
Approximate Variety Description Origin Ripening Uses Yellow Transparent Tart, crisp Imported from Russia by USDA in 1870s Early July All-purpose Lodi Tart, somewhat firm New York, Early 1900s. Montgomery x Transparent. Early July Baking, sauce Pristine Sweet-tart PRI (Purdue Rutgers Illinois) release, 1994. Mid-late July All-purpose Dandee Red Sweet-tart, semi-tender New Ohio variety. An improved PaulaRed type. Early August Eating, cooking Redfree Mildly tart and crunchy PRI release, 1981. Early-mid August Eating Sansa Sweet, crunchy, juicy Japan, 1988. Akane x Gala. Mid August Eating Ginger Gold G. Delicious type, tangier G Delicious seedling found in Virginia, late 1960s. Mid August All-purpose Zestar! Sweet-tart, crunchy, juicy U Minn, 1999. State Fair x MN 1691. Mid August Eating, cooking St Edmund's Pippin Juicy, crisp, rich flavor From Bury St Edmunds, 1870. Mid August Eating, cider Chenango Strawberry Mildly tart, berry flavors 1850s, Chenango County, NY Mid August Eating, cooking Summer Rambo Juicy, tart, aromatic 16th century, Rambure, France. Mid-late August Eating, sauce Honeycrisp Sweet, very crunchy, juicy U Minn, 1991. Unknown parentage. Late Aug.-early Sept. Eating Burgundy Tart, crisp 1974, from NY state Late Aug.-early Sept. All-purpose Blondee Sweet, crunchy, juicy New Ohio apple. Related to Gala. Late Aug.-early Sept. Eating Gala Sweet, crisp New Zealand, 1934. Golden Delicious x Cox Orange. Late Aug.-early Sept. Eating Swiss Gourmet Sweet-tart, juicy Switzerland. Golden x Idared. Late Aug.-early Sept. All-purpose Golden Supreme Sweet, Golden Delcious type Idaho, 1960. Golden Delicious seedling Early September Eating, cooking Pink Pearl Sweet-tart, bright pink flesh California, 1944, developed from Surprise Early September All-purpose Autumn Crisp Juicy, slow to brown Golden Delicious x Monroe. -

Ästhetische Bildung Im Museum Sinclair-Haus
MUSEUM SINCLAIR-HAUS | BLATTWERKE 03 | »FRÜCHTE« SEITE 01 Stellen Sie sich vor, Sie sitzen ausschließlich in ihrem Küchenraum, er wäre Ihre ganze Welt. Sie verfolgen selbst die unscheinbarsten Anregungen. Etwas Mehl an Ihren Händen wird zu Schneeverwehungen, siedendes Wasser zu Gischt in einem Bergbach, und das dazugehörende Geräusch aus der Pfanne lässt Sie an eine wilde Kanufahrt denken. Allein die Umbenennung einer Küche in ein Atelier bewirkt, was Umbenennungen mit sich bringen können: Die Wahrnehmung verändert sich. Peter Jenny Weshalb gibt es Früchte? Warum steckt eine Pflanze So vielfältig die Formen und Farben von Früchten sind, soviel Energie in das Hervor- ebenso vielfältig ist die Darstellung von Früchten in der bringen von Früchten? Kunst: In Malerei, Fotografie, Zeichnung oder Skulptur. Seit hunderten von Jahren zeigen Künstlerinnen und Künstler Früchte als Zeichen für Leben und Vitalität, aber auch für Vergänglichkeit und Verfall. Die folgende Zusammenstellung vereint unterschiedliche künst- lerische und experimentelle Ideen rund um die Frucht und richtet sich an Kinder, Lehrer/innen und Erzieher/innen. MUSEUM SINCLAIR-HAUS | BLATTWERKE 03 | »FRÜCHTE« SEITE 02 Was ist eine Frucht? Nicht alles was wir in der Obst- und Gemüseabteilung eines Supermarktes finden darf man „Frucht“ nennen. Eine Frucht ist das Organ einer Pflanze, das die Samen bis zur Reife umschließt und dann zu ihrer Ausbreitung dient. Früchte gehen aus Blüten hervor. Eine Frucht ist also eine verblühte Blüte im Zustand der Samenreife. Dieses sind keine Früchte, da sie nicht aus einer Blüte hervorgehen und auch keinen Samen enthalten: - Kartoffel, sie ist eine Sprossknolle und wächst unter der Erde. - Zwiebel, sie ist ein unterirdisches Speicherorgan aus der die Zwiebelpflanze hervorgeht. -

Cedar-Apple Rust
DIVISION OF AGRICULTURE RESEARCH & EXTENSION Agriculture and Natural Resources University of Arkansas System FSA7538 Cedar-Apple Rust Stephen Vann Introduction Assistant Professor One of the most spectacular Extension Urban Plant Pathologist diseases to appear in spring is cedar- apple rust. This disease is caused by the fungus Gymnosporangium juniperi-virginianae and requires both cedar and apple trees to survive each year. It is mainly a problem in the eastern portion of North America and is most important on apple or crab Figure 2. Cedar-apple rust on crabapple apple (Malus sp), but can also affect foliage. quince and hawthorn. yellow-orange color (Figures 1 and 2). Symptoms On the upper leaf surface of these spots, the fungus produces specialized The chief damage by this disease fruiting bodies called spermagonia. On occurs on apple trees, causing early the lower leaf surface (and sometimes leaf drop and poor quality fruit. This on fruit), raised hair-like fruiting bod can be a significant problem to com ies called aecia (Figure 3) appear as mercial apple growers but also harms microscopic cup-shaped structures. the appearance of ornamental crab Wet, rainy weather conditions favor apples in the home landscape. On severe infection of the apple. The apple, symptoms first appear as fungus forms large galls on cedar trees small green-yellow leaf or fruit spots in the spring (see next section), but that gradually enlarge to become a these structures do not greatly harm Arkansas Is Our Campus Visit our web site at: Figure 1. Cedar-apple rust (leaf spot) on Figure 3. Aecia of cedar-apple rust on https://www.uaex.uada.edu apple (courtesy J. -

Print Open Colour Acceptances
PRINT OPEN COLOUR ACCEPTANCES AUSTRALIA Vicki Moritz EFIAP/p APSEM Thunder Point Lighthouse GMPSA APP BELGIUM Maurits De Groen Triangles Sara Gabriels EPSA Second class Wrinkles of life Luc Stalmans Diffraction in a spider web Somnium Verum Evadit The Rope CHANNEL ISLANDS Steven Le Prevost FRPS AFIAP Sidney GPU Ribbon MPAGB FIPF Meadowgrove Farm Sophie and Susan CHINA Yin Ba Joyful song in the desert SPS Medal Medal Morning glow in the mist Ji Chen Joy The couple Shaohua Chen Eye Face Mending net Tao Feng Left-behind children Jian Kang Mettled horses Xinjiang body prairie Jianping Li Basha matador Eullient Lusheng Festival Take across semtient beings Jiangchuan Tong Vestrahorn in Iceland 2 Yonghe Wang Sevent steeds compete SPS Ribbon Bo Xu Born of fire Sisong Yang Wrangler SPS Ribbon Du Yi Over the rainbow Strange dream Changren Yu Herdsman 4 SPS Ribbon Herdsman 2 Herdsman 3 ENGLAND Gerry Adcock ARPS Names Can't Hurt Me Terri Adcock LRPS CPAGB AFIAP Chasing the Pack PPSA Dave Airston LRPS CPAGB Gracefulness Warren Alani ARPS DPAGB AFIP Full Thrust BPE***** Maria On The Ball Eagerness PSA Silver Medal Helen Ashbourne ARPS DPAGB Dance Dancer in Pink Dancing the Blues Charles Edward Ashton ARPS Bidri Production Hyderabad DPAGB BPE3 AFIAP Metalwork Poultry Processing Kerala Purple Portrait Barry Badcock ARPS Passing John Birch MAXIMUM POWER Francesca Bramall Isolation Soft Wash Of Waves Winter Landscape At Sandon David Bray Stormy Day At Godrevy Vulcan Reflection At Dusk Joe Brennan LRPS DPAGB BPE3* Innocent Lorna Brown ARPS EFIAP CPAGB Nest -

Survey of Apple Clones in the United States
Historic, archived document Do not assume content reflects current scientific knowledge, policies, or practices. 5 ARS 34-37-1 May 1963 A Survey of Apple Clones in the United States u. S. DFPT. OF AGRffini r U>2 4 L964 Agricultural Research Service U.S. DEPARTMENT OF AGRICULTURE PREFACE This publication reports on surveys of the deciduous fruit and nut clones being maintained at the Federal and State experiment stations in the United States. It will b- published in three c parts: I. Apples, II. Stone Fruit. , UI, Pears, Nuts, and Other Fruits. This survey was conducted at the request of the National Coor- dinating Committee on New Crops. Its purpose is to obtain an indication of the volume of material that would be involved in establishing clonal germ plasm repositories for the use of fruit breeders throughout the country. ACKNOWLEDGMENT Gratitude is expressed for the assistance of H. F. Winters of the New Crops Research Branch, Crops Research Division, Agricultural Research Service, under whose direction the questionnaire was designed and initial distribution made. The author also acknowledges the work of D. D. Dolan, W. R. Langford, W. H. Skrdla, and L. A. Mullen, coordinators of the New Crops Regional Cooperative Program, through whom the data used in this survey were obtained from the State experiment stations. Finally, it is recognized that much extracurricular work was expended by the various experiment stations in completing the questionnaires. : CONTENTS Introduction 1 Germany 298 Key to reporting stations. „ . 4 Soviet Union . 302 Abbreviations used in descriptions .... 6 Sweden . 303 Sports United States selections 304 Baldwin. -

Handling of Apple Transport Techniques and Efficiency Vibration, Damage and Bruising Texture, Firmness and Quality
Centre of Excellence AGROPHYSICS for Applied Physics in Sustainable Agriculture Handling of Apple transport techniques and efficiency vibration, damage and bruising texture, firmness and quality Bohdan Dobrzañski, jr. Jacek Rabcewicz Rafa³ Rybczyñski B. Dobrzañski Institute of Agrophysics Polish Academy of Sciences Centre of Excellence AGROPHYSICS for Applied Physics in Sustainable Agriculture Handling of Apple transport techniques and efficiency vibration, damage and bruising texture, firmness and quality Bohdan Dobrzañski, jr. Jacek Rabcewicz Rafa³ Rybczyñski B. Dobrzañski Institute of Agrophysics Polish Academy of Sciences PUBLISHED BY: B. DOBRZAŃSKI INSTITUTE OF AGROPHYSICS OF POLISH ACADEMY OF SCIENCES ACTIVITIES OF WP9 IN THE CENTRE OF EXCELLENCE AGROPHYSICS CONTRACT NO: QLAM-2001-00428 CENTRE OF EXCELLENCE FOR APPLIED PHYSICS IN SUSTAINABLE AGRICULTURE WITH THE th ACRONYM AGROPHYSICS IS FOUNDED UNDER 5 EU FRAMEWORK FOR RESEARCH, TECHNOLOGICAL DEVELOPMENT AND DEMONSTRATION ACTIVITIES GENERAL SUPERVISOR OF THE CENTRE: PROF. DR. RYSZARD T. WALCZAK, MEMBER OF POLISH ACADEMY OF SCIENCES PROJECT COORDINATOR: DR. ENG. ANDRZEJ STĘPNIEWSKI WP9: PHYSICAL METHODS OF EVALUATION OF FRUIT AND VEGETABLE QUALITY LEADER OF WP9: PROF. DR. ENG. BOHDAN DOBRZAŃSKI, JR. REVIEWED BY PROF. DR. ENG. JÓZEF KOWALCZUK TRANSLATED (EXCEPT CHAPTERS: 1, 2, 6-9) BY M.SC. TOMASZ BYLICA THE RESULTS OF STUDY PRESENTED IN THE MONOGRAPH ARE SUPPORTED BY: THE STATE COMMITTEE FOR SCIENTIFIC RESEARCH UNDER GRANT NO. 5 P06F 012 19 AND ORDERED PROJECT NO. PBZ-51-02 RESEARCH INSTITUTE OF POMOLOGY AND FLORICULTURE B. DOBRZAŃSKI INSTITUTE OF AGROPHYSICS OF POLISH ACADEMY OF SCIENCES ©Copyright by BOHDAN DOBRZAŃSKI INSTITUTE OF AGROPHYSICS OF POLISH ACADEMY OF SCIENCES LUBLIN 2006 ISBN 83-89969-55-6 ST 1 EDITION - ISBN 83-89969-55-6 (IN ENGLISH) 180 COPIES, PRINTED SHEETS (16.8) PRINTED ON ACID-FREE PAPER IN POLAND BY: ALF-GRAF, UL. -

Fruitteeltpraktijkonderz
FRUITTEELTPRAKTIJKONDERZOEK jaarverslag 1995 Proefstation voor de Fruitteelt - Wilhelminadorp Proeftuin Noord-Brabant - Breda Fruitteeltproeftuin Midden-Nederland - Geldermalsen Fruitteeltproeftuin voor Limburg en Noord-Brabant - Horst Fruitteeltproeftuin voor Noord-Nederland - Zeewolde Het Fruitteeltpraktijkonderzoek (FPO) verricht het praktijkgerichte onderzoek voor de sector fruitteelt. Het onderzoek wordt gezamenlijk gefinancierd door het Ministerie van Landbouw, Natuurbeheer en Visserij, het Landbouwschap en het Produktschap voor Siergewassen (PVS). Postbus 20401, 2500 EK Den Haag landbouwrnatuü'rbeheer Tel.07 0379391 1 en visserij — Landbouwschap Prinsenvinkenpark 19, 2585 HK Den Haag Tel. 070 3526666 oov Postbus 93099, 2509 AB Den Haag Tel. 070 3041234 PROEFSTATION VOOR DE FRUITTEELT Brugstraat 51 4475 AN Wilhelminadorp, Nederland Telefoon : 0113-242500 Fax : 0113-242650 Postgironr 495017 Overname van gedeelten van dit jaarverslag, alsmede van gegevens, is uitsluitend toegestaan na vooraf verkregen toestemming en bronvermelding. Het Proefstation stelt zich niet aansprakelijk voor eventuele schadelijke gevolgen, ontstaan door gebruik van de gegevens die in deze uitgave zijn gepubliceerd. Prijs f 25,00 ISSN 0168-7689 Jaarverslag FPO 1995 INHOUD Blz Begunstigers 1 Opmerkingen over merken vn gewasbeschermingsmiddelen 1 Voorwoord 2 Bestuur 3 Medewerkers 5 Algemeen 9 Bestuur - programmering - personeel - voorlichtings activiteiten - lezingen - buitenlandse reizen De Proeftuin 17 Het weer in 1995 - bloei Afdeling Teelt en Economie Sectie -

Effect of Cultivar, Position of Fruits in Tree-Crown and of Summer Pruning on Surface Temperature of Apples and Pears, Ejpau, 15(2), #03
Electronic Journal of Polish Agricultural Universities (EJPAU) founded by all Polish Agriculture Universities presents original papers and review articles relevant to all aspects of agricultural sciences. It is target for persons working both in science and industry, regulatory agencies or teaching in agricultural sector. Covered by IFIS Publishing (Food Science and Technology Abstracts), ELSEVIER Science - Food Science and Technology Program, CAS USA (Chemical Abstracts), CABI Publishing UK and ALPSP (Association of Learned and Professional Society Publisher - full membership). Presented in the Master List of Thomson ISI. ELECTRONIC 2012 JOURNAL Volume 15 OF POLISH Issue 2 AGRICULTURAL Topic HORTICULTURE UNIVERSITIES Copyright © Wydawnictwo Uniwersytetu Przyrodniczego we Wrocławiu, ISSN 1505-0297 LIPA T., LIPECKI J., JANISZ A., 2012. EFFECT OF CULTIVAR, POSITION OF FRUITS IN TREE-CROWN AND OF SUMMER PRUNING ON SURFACE TEMPERATURE OF APPLES AND PEARS, EJPAU, 15(2), #03. Available Online http://www.ejpau.media.pl EFFECT OF CULTIVAR, POSITION OF FRUITS IN TREE-CROWN AND OF SUMMER PRUNING ON SURFACE TEMPERATURE OF APPLES AND PEARS Tomasz Lipa, Janusz Lipecki, Anna Janisz Departament of Pomology, University of Life Sciences in Lublin, Poland ABSTRACT Extensive studies (2006–2009) on the influence of apple and pear fruit surface temperature, in dependence on the fruit position in tree canopy and summer pruning, were conducted in a commercial orchard in Lublin district, Poland. There was a significant effect of fruit position in the canopy on heat accumulation in fruit surface. Fruits born in southern part of the canopy were more heated than those from other tree parts. It was found that a blush contributed to an increase of fruit temperature, especially those from southern parts of the canopy. -
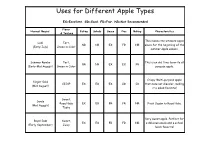
Uses for Different Apple Types
Uses for Different Apple Types EX=Excellent, GD=Good, FR=Fair, NR=Not Recommended Flavor Harvest Begins: Eating Salads Sauce Pies Baking Characteristics & Texture This makes the ultimate apple Lodi Tart, NR NR EX FR NR sauce for the beginning of the (Early July) Green in Color summer apple season. Summer Rambo Tart, This is an old-time favorite all- NR NR EX EX FR (Early-Mid August) Green in Color purpose apple. Crispy Multi-purpose apple Ginger Gold CRISP EX EX EX GD GD that does not discolor, making (Mid August) it a salad favorite! Sweet, Sansa Royal Gala EX EX FR FR NR First Cousin to Royal Gala. (Mid August) Taste Very sweet apple. Perfect for Royal Gala Sweet, EX EX FR FR NR a delicous snack and a school (Early September) Juicy lunch favorite! Extremely popular sweet Honey Crisp tasting apple. Our most crispy CRISP EX EX EX EX FR (Early September) and juiciest apple perfect for a sweet snack! MacIntosh Semi-Sweet/ General all purpose apple. EX GD EX EX FR (Mid September) Tart Nice sweet-tart apple. Exclusively sold at Milburn Orange Honey Sweet, EX EX EX EX FR Orchards. Some say equal to (Mid September) Crisp Honey Crisp! Crispy, tart flavor. This apple is available before Stayman Jonathan CRISP/ EX GD GD EX EX Winesap and a perfect (Mid September) Tart substitute. Multi-Purpose apple. Cortland Semi- Multi-Purpose apple. Next GD GD EX EX FR (Mid September) Tart best thing to MacIntosh. Sweet, An offspring of Fuji, same September Fuji Juicy, EX EX GD EX GD qualities but 4 weeks (Mid September) Not very earlier. -
![United States Patent [191 [11] Patent Number: Plant 7,814 Mckenzie, Deceased Et Al](https://docslib.b-cdn.net/cover/0475/united-states-patent-191-11-patent-number-plant-7-814-mckenzie-deceased-et-al-1280475.webp)
United States Patent [191 [11] Patent Number: Plant 7,814 Mckenzie, Deceased Et Al
USO0PPO7814P United States Patent [191 [11] Patent Number: Plant 7,814 McKenzie, deceased et al. [45] Date of Patent: Mar. 3, 1992 [54] APPLE TREE NAMED ‘SCIROS' [56] References Cited U.S. PATENT DOCUMENTS [75] IIlv¢m°r$= D0" McKenzie’ deceased, late 0f _ 15.11. 2,460 12/1964 Roberts ................................ .. Plt. 34 Havelock North; by_J0yPM¢I%mz1e, P.P. 3,637 10/1974 McKenzie ........................... .. P1t.34 Gin Primary Examiner-James R. Feyrer whit'e, K1) 2, Hastings, an of New Attorney, Agent, or Firm-Quarles 8; Brady Zealand - [57] ABSTRACT The new and distinct variety is a selection from seed [21] Appl. No.: 566,285 lings derived from crossing the apple varieties known as - “Gala” (U.S. Plant Pat. No. 3,637) and “Splendour” . _ (U .5. Plant Pat. No. 2,460). The fruit of the apple tree of [22] Filed‘ Aug‘ 13’ 1990 this new variety has an attractive appearance character ized by its overall bright red color pattern. The new [51] Int. Cl.5 ............................................. .. A01H 5/00 variety has been named “Sciros”. - [52] US. Cl. .. Plt./34 [58] Field of Search . .. Pit/34 1 Drawing Sheet 1 2 SUMMARY OF THE INVENTION DETAILED DESCRIPTION OF THE The new variety was selected from a population seed DISCLOSURE lings derived from crossing the apple varieties “Splen The following is a detailed description of the new dour” (U.S. Plant Pat. No. 2,460) and “Gala” (US. 5 variety with color terminology in accordance with The Plant Pat. No. 3,637) in 1984. The new variety was Royal Horticultural Society Colour Chart (RHSCC) distinguishable from the parent varieties Splendour and except where general color terms of ordinary meaning Gala as well as the varieties Sciray; Sciglo; and Scieur are used as is clear from the context.