DOCSLIB.ORG

10. Cavity Theory

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
10. Cavity Theory Outline • Problem statement Cavity Theory • Bragg-Gray cavity theory • Spencer cavity theory Chapter 10 • Burlin cavity theory • Dose near interfaces between F.A. Attix, Introduction to Radiological dissimilar media Physics and Radiation Dosimetry • Summary Cavity Theory: Problem Statement Bragg-Gray Theory • Homogeneous medium, Q wall (w) • Probe - cavity - thin layer of gas (g) • Charged particles crossing + - w-g interface gas • Objective: find a relation Dg between the dose in a probe wall to that in the medium (A) A fluence of charged particles crossing an interface between media w and g Dw (B) A fluence of charged particles passing through a thin layer of medium g • Basis for dosimetry sandwiched between regions contain medium w Fluence is assumed to be continuous across all interfaces; it is related to the dose Bragg-Gray Theory Bragg-Gray Theory • Charged particles of fluence • Two conditions: , kinetic energy T – Thickness of g layer is much smaller than the range of charged particles (medium g is close to w in atomic • Dg, Dw - absorbed doses on number) each side of the boundary – The absorbed dose in the cavity is deposited entirely by dT the charged particles crossing it • dx - mass collision stopping c • Additional assumptions: power, evaluated at energy T – Existence of CPE • Assuming continuous – Absence of bremsstrahlung generation across the interface – No backscattering 1 Bragg-Gray Theory Bragg-Gray Theory For differential energy distribution T, average mass For charge Q (of either sign) produced in gas of mass m by collision stopping power radiation, the dose in gas Tmax dT Q W Tmax dT ΦT dT Dg ΦT dT 0 dx 0 dx c,g m e g c,w S S m g Tmax m w Tmax Then the B-G relation expressed in terms of cavity ionization: T dT T dT 0 0 T T 1 max dT Dg Q W w 1 max dT Dw T dT Dw m Sg T dT 0 0 dx m e dxc,w c,g g This equation allows calculating the absorbed dose in the medium Dw m Sw w immediately surrounding a B-G cavity, based on the charge m Sg produced in the cavity gas, provided that the parameters are known Dg m Sg Bragg-Gray Theory Bragg-Gray Theory w • First Bragg-Grey Corollary: two different • As long as m S g is evaluated for the charged-particle gases filling the cavity spectrum T that crosses the cavity, the B-G relation requires neither CPE nor a homogeneous field of radiation Q V W / e g 2 2 1 2 • The charged-particle fluence must be the same in the m Sg T Q V W / e 1 cavity and in the medium w 1 1 2 • If CPE does exist in the neighborhood of a point of interest • Second Bragg-Grey Corollary: two chambers in the medium w, then the insertion of a B-G cavity at the (walls) of different volume and material point may be assumed not to perturb the “equilibrium w1 Q V en / S spectrum” of charged particles existing there 2 2 w2 m g Q V / S w2 1 1 en w1 m g Spencer derivation of B-G Spencer derivation of B-G • The absorbed dose at any point in the undisturbed • Consider a small cavity filled with medium g, medium w where CPE exists: surrounded by a homogeneous medium w that CPE contains a homogeneous source emitting N Dw Kw NT0 (MeV/g) identical charged particles per gram, each with • For an equilibrium charged-particle fluence spectrum e kinetic energy T0 (MeV) T the absorbed dose T • The cavity is assumed to be far enough from the 0 e dT Dw T dT outer limits of w that CPE exists 0 dxw • Both B-G conditions are assumed to be satisfied • Then the spectrum by the cavity, and bremsstrahlung generation is e N assumed to be absent T dT dxw 2 Spencer derivation of B-G Spencer derivation of B-G Start with mono- • Assuming the same spectrum on both sides, ratio energetic source of the dose in the cavity to that of the medium w of T0=2MeV T0 Dg 1 dT dxg g dT S D T dT dx m w w 0 0 w • Can be generalized to accommodate bremsstrahlung generation by electrons T0 e Dg 1 dT dxc,g • Example of an equilibrium fluence spectrum, T = N/(dT/dx), dT S g of primary electrons under CPE conditions in water, assuming D T 1Y T dT dx m w the continuous-slowing-down approximation w 0 w 0 0 c,w B-G Cavity Theory vs. Experiment Averaging of Stopping Powers • Extend a single starting energy T0 to a distribution T (spectrum): stopping power has to be integrated over the distribution T Averaging over T T max 0 each T0, and over dT dxc,g N dT T for each T0 T0 Dg 0 0 dT dxw g m Sw D Tmax w N T 1Y Y dT T0 0 w 0 0 0 • Ratio of collision stopping powers is a slowly varying Comparison of measured ionization densities (solid curves) in flat air-filled ion function, therefore average energy T may be used chambers having various wall materials and adjustable gap widths, with Bragg-Gray theory (tick marks at left) and Spencer theory (dashed curves), for 198Au rays B-G Cavity Theory vs. Experiment Spencer Cavity Theory • Experiments had shown deviations from B-G theory • Goals: to account for d-rays and cavity size effect • Dependence on cavity size and Z • Starts with two B-G conditions (narrow g region and • For walls of high atomic number d-ray dose produced by crossing particles) and two production becomes an issue additional assumptions (existence of CPE and absence of bremsstrahlung generation) – d-rays cross the cavity with the rest of electrons • Introduces mean energy D, needed to cross the cavity – they change spectrum, enhancing low energy part • Based on their energy T, electrons in a spectrum are • Spencer theory divided into „fast‟ ( T D ) and „slow‟ ( T D ) groups 3 Spencer Cavity Theory Spencer Cavity Theory e,d e Approximate Values of R(T0,T) = T/ T, the Ratio of the • For monoenergetic electron beam with T0 emitting N particles Differential Electron Fluences with and without d-rays per gram through a homogeneous medium w the absorbed dose is expressed in terms of restricted stopping power CPE T D NT 0 e,d S T, D dT w0 D T m w • The equilibrium spectrum including d-rays NR(,) T T e,d 0 T dT/ dx w • R(T,T0) – ratio of differential electron fluence, including d-rays to that of primary electrons alone Spectrum enhanced many-fold at low electron energies Spencer Cavity Theory Spencer Cavity Theory • Taking into account adjustment for electron spectrum, dose to the wall CPE T0 RTT(,) D NT N0 S T, D dT w0 D dT/ dx m w w • D regulates the cavity size; for D=0 • Dose to the cavity Spencer Cavity Theory Spencer Cavity Theory cavity size • Ratio of doses in cavity and wall T 0 RTT(,)0 DmgS(,) T dT D dT/ dx Dg w T0 RTT(,) Dw 0 DmwS(,) T dT D dT/ dx w • Works well for small cavities (electron range is much larger than the cavity size) • If actual spectrum of crossing charged particles is Values of Dg/Dw Calculated for Air Cavities by Spencer from Spencer Cavity known, can replace the ratio term Theory, vs. Bragg-Gray Theory Better agreement between Spencer and B-G for large cavity sizes 4 Spencer Cavity Theory Burlin Cavity Theory • The Spencer cavity theory gives somewhat better • -ray cavity theory, for intermediate cavity size agreement with experimental observations for small cavities than does simple B-G theory, by taking account of d-ray production and relating the dose integral to the cavity size • However, it still relies on the B-G conditions, and therefore fails to the extent that they are violated • In particular, in the case of cavities that are large small intermediate large (i.e., comparable to the range of the secondary charged particles generated by indirectly ionizing radiation), neither B-G condition is satisfied e1 – crossers e3 – stoppers e2 – starters e4 – insiders Burlin Cavity Theory Burlin Cavity Theory To arrive at a usefully simple theory Burlin made the following assumptions, either explicitly or implicitly: electrons generated in the cavity 1. The media w and g are homogeneous. - 2. A homogeneous -ray field exists everywhere throughout w and g. (This e means that no -ray attenuation correction) 3. Charged-particle equilibrium exists at all points that are farther than the max electron range from the cavity boundary 4. The equilibrium spectra of secondary electrons generated in w and g are electrons generated the same in the wall 5. The fluence of electrons entering from the wall is attenuated exponentially as it passes through the medium g, without changing its spectral distribution. 6. The fluence of electrons that originate in the cavity builds up to its equilibrium value exponentially as a function of distance into the cavity, according to the same attenuation coefficient that applies to the incoming electrons Burlin Cavity Theory • Cavity relation accounts for 2 sources of electrons Burlin Cavity Theory depositing dose g • Parameter d~1 for small, d~0 for large Dg g en d mw S (1 d ) cavities Dw w • The corresponding relation for 1 – d, • Parameter is related to the cavity size, expressed as representing the average value of /e L g g el e dl L throughout the cavity: w 0 w 1 e d e L e L L w dl el 0 w 1 e dl L g 0 g Le1 • l is the distance (cm) of any point in the cavity from the 1d e L e L wall, along a mean chord of length L g dl 0 g 5 Burlin Cavity Theory Burlin Cavity Theory e e • For the nonhomogeneous case where g w, ( w g) • Moreover, if the -value of the cavity medium for the wall • Theory works well for wide range of cavity sizes electrons is not the same as for the cavity-generated and materials electrons, due to a difference in spectral distributions, then • Parameter estimated for air-filled cavity in general g 16 dd (1 ) e 1.4 g Tmax 0.036 and hence etmax 0.01 dd1 • The
Load more

Recommended publications
  • ACUTE RADIATION SYNDROME: Diagnosis and Treatment
    ACUTE RADIATION SYNDROME: Diagnosis and Treatment Badria Al Hatali, MD Medical Toxicologist Department of Environmental and Occupational Health MOH - Oman Objectives Provide a review of radiation basics and acute radiation sickness Discuss diagnostic tools and triage tools for Acute Radiation Syndromes Discuss management of Acute Radiation Syndromes Energy traveling over a distance as Waves Particles • Gamma rays • Alpha • X-rays • Beta • Radio waves • neurons Non-ionizing vs Ionizing Radiation • High energy • Low energy • Removes orbital electrons • Does not remove orbital from atoms > DNA electrons from atom damage Radioactive Decay Process to Remove excess energy from atomic nuclei Nuclei emit rays or particles to decrease nuclear energy Radioactive materials have unstable nuclei with excess energy Ionizing Radiation Dose • Radiation absorb dose (RAD): the amount of energy absorbed by the body. 1 cGy = 0.01 J/kg (USA) • Gray (Gy): expressed as absorbed energy per unit mass of tissue. 100 rad =100 cGy =1 J/kg (SI) • Roentgen Equivalent Man (REM) relates the absorbed dose in human tissue to the effective biological damage of the radiation (USA) • Sievert (Sv): the absorbed dose in human tissue to the effective biological damage of the radiation (SI) Radioactivity Biological And Effective Half-lives Biological half-life is the time to remove half of radioactive element from body Effective half-life is the combined effect of radioactive decay & biological elimination Effective half-life is always shorter than either physical or biological half-lives Biological Effects of Ionizing Radiation Direct damage Chromosome Other biochemical E.g. alpha and beta particles Indirect damage Chemical changes due to radiolysis of water in cell E.g.
    [Show full text]
  • Emergency and Combat First Aid» Module № 1 Emergency and Combat First Aid Topic 7 Means of Mass Destruction
    Ministry of Health of Ukraine Ukrainian Medical stomatological Academy It is ratified On meeting department Of accident aid and military medicine «___»_____________20 __y. Protocol №_____ Manager of department DMSc ., assistant professor __________К.Shepitko METHODICAL INSTRUCTION FOR INDEPENDENT WORK OF STUDENTS DURING PREPARATIONS FOR THE PRACTICAL LESSON Educational discipline «Emergency and Combat First Aid» Module № 1 Emergency and Combat First Aid Topic 7 Means of Mass Destruction. First Aid. Weapons of mass destructions. Lesson 10 Radiations chemical accidents .First Aid Сourse ІІ Foreing students training dentistry Faculty Training of specialists of the second (master) level of higher of education (название уровня высшего образования) Areas of knowledge _______ 22 «Health protection»_________ (шифр и название области знаний) Specialty ________222 «Medicine», 221 «Stomatology»________________ (код и наименование специальности) Poltava 2019 The relevance of the topic: Military action in modern warfare will be carried out with high activity and limit tension. They cause great losses in the army and among the population, the destruction of potentially dangerous objects, energy centers, waterworks, the formation of large zones of destruction, fires and floods. The main form of countering in the war, is armed struggle - the organized use of armed forces and weapons to achieve specific political and military objectives, a combination of military actions of varying scales. To conventional weapons, the application of which may cause losses among the population are missiles and aerial munitions, including precision munitions volumetric detonation of cluster and incendiary. Have the greatest efficiency high precision conventional weapons, which provide automatic detection and reliable destruction of targets and enemy targets with a single shot (trigger).
    [Show full text]
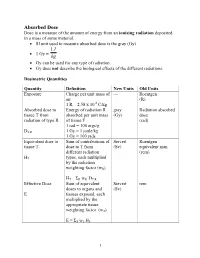
  • Absorbed Dose Dose Is a Measure of the Amount of Energy from an Ionizing Radiation Deposited in a Mass of Some Material
    Absorbed Dose Dose is a measure of the amount of energy from an ionizing radiation deposited in a mass of some material. • SI unit used to measure absorbed dose is the gray (Gy). 1J • 1 Gy = kg • Gy can be used for any type of radiation. • Gy does not describe the biological effects of the different radiations. Dosimetric Quantities Quantity Definition New Units Old Units Exposure Charge per unit mass of --- Roentgen air (R) 1 R = 2.58 x 10-4 C/kg Absorbed dose to Energy of radiation R gray Radiation absorbed tissue T from absorbed per unit mass (Gy) dose radiation of type R of tissue T (rad) 1 rad = 100 ergs/g DT,R 1 Gy = 1 joule/kg 1 Gy = 100 rads Equivalent dose to Sum of contributions of Sievert Roentgen tissue T dose to T from (Sv) equivalent man different radiation (rem) HT types, each multiplied by the radiation weighting factor (wR) HT = ΣR wR DT,R Effective Dose Sum of equivalent Sievert rem doses to organs and (Sv) E tissues exposed, each multiplied by the appropriate tissue weighting factor (wT) E = ΣT wT HT 1 Radiological Protection For practical purposes of assessing and regulating the hazards of ionizing radiation to workers and the general population, weighting factors (previously called quality factors, Q) are used. A radiation weighting factor is an estimate of the effectiveness per unit dose of the given radiation relative a to low-LET standard. Weighting factors are dimensionless multiplicative factors used to convert physical dose (Gy) to equivalent dose (Sv) ; i.e., to place biological effects from exposure to different types of radiation on a common scale.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
  • Office of Radiation Protection
    How is Dose Measured? July 2002 Fact Sheet 320-058 Division of Environmental Health Office of Radiation Protection RADIATION DOSE When radioactive material decays and the transformation of the atom occurs there is characteristic energy that is released. This energy is released in the form of what we call radiation. There are different types of radiation, but they all serve the same general purpose, ridding the atom of excess energy after it transforms. These radiations travel until, by losing energy, they “stop”. Radiation loses its energy by interacting with atoms in its pathway and transferring energy to the atom during these interactions. When an interaction with radiation removes an electron from the atom it is called ionization. Other types of interactions include the excitation of an atom, the breaking of molecular bonds, and the heating of an atom or molecule. Ionization, excitation, and molecular bond breaking can cause biological damage; heat transfer does not necessarily cause biological damage. The purely physical event of energy deposited by a radiation in a given volume of material, i.e. tissue, is called the absorbed dose. The unit of absorbed dose is called the Rad, the international unit is the Gray (gy). The absorbed dose quantifies the amount of energy transferred to a volume of material, but it does not reflect the biological damage that potentially occurred. Because of the physics of radiation, the biological effect of the same amount of absorbed energy may vary according to the type of the radiation. A quality factor, Q was developed, to be able to compare absorbed doses from different radiation types.
    [Show full text]
  • Chapter 2: Dosimetricprinciples, Quantitiesandunits
    Chapter 2: Dosimetric Principles, Quantities and Units Set of 131 slides based on the chapter authored by J.P. Seuntjens, W. Strydom, and K.R. Shortt of the IAEA publication (ISBN 92-0-107304-6): Review of Radiation Oncology Physics: A Handbook for Teachers and Students Objective: To familiarize the student with the basic principles of the quantities used in dosimetry for ionizing radiation. Slide set prepared in 2006 by G.H. Hartmann (Heidelberg, DKFZ) Comments to S. Vatnitsky: [email protected] Version 2012 IAEA International Atomic Energy Agency CHAPTER 2. TABLE OF CONTENTS 2.1 Introduction 2.2 Radiation field quantities (also denoted as Radiometric quantities) 2.3 Dosimetrical quantities: fundamentals 2.4 Dosimetrical quantities 2.5 Interaction coefficients: electrons 2.6 Interaction coefficients: photons 2.7 Relation between radiation field and dosimetric quantities 2.8 Cavity theory IAEA Review of Radiation Oncology Physics: A Handbook for Teachers and Students - 2.Slide 1 2.1 INTRODUCTION Radiation dosimetry has its origin in the medical application of ionizing radiation starting with the discovery of x-rays by Röntgen in 1895. In particular • the need of protection against ionizing radiation, • the application in medicine required quantitative methods to determine a "dose of radiation". The purpose of a quantitative concept of a dose of radiation is: • to predict associated radiation effects (radiation detriments) • to reproduce clinical outcomes. IAEA Review of Radiation Oncology Physics: A Handbook for Teachers and Students - 2.1. Slide 1 2.1 INTRODUCTION The connection to the medical profession is obvious. The term dose of radiation was initially used in a pharmacological sense, that means: analogously to its meaning when used in prescribing a dose of medicine.
    [Show full text]
  • Q: What's the Difference Between Roentgen, Rad and Rem Radiation Measurements?
    www.JICReadiness.com Q: What's the Difference Between Roentgen, Rad and Rem Radiation Measurements? A: Since nuclear radiation affects people, we must be able to measure its presence. We also need to relate the amount of radiation received by the body to its physiological effects. Two terms used to relate the amount of radiation received by the body are exposure and dose. When you are exposed to radiation, your body absorbs a dose of radiation. As in most measurement quantities, certain units are used to properly express the measurement. For radiation measurements they are... Roentgen: The roentgen measures the energy produced by gamma radiation in a cubic centimeter of air. It is usually abbreviated with the capital letter "R". A milliroentgen, or "mR", is equal to one one-thousandth of a roentgen. An exposure of 50 roentgens would be written "50 R". Rad: Or, Radiation Absorbed Dose recognizes that different materials that receive the same exposure may not absorb the same amount of energy. A rad measures the amount of radiation energy transferred to some mass of material, typically humans. One roentgen of gamma radiation exposure results in about one rad of absorbed dose. Rem: Or, Roentgen Equivalent Man is a unit that relates the dose of any radiation to the biological effect of that dose. To relate the absorbed dose of specific types of radiation to their biological effect, a "quality factor" must be multiplied by the dose in rad, which then shows the dose in rems. For gamma rays and beta particles, 1 rad of exposure results in 1 rem of dose.
    [Show full text]
  • Radiation Dose Associated with Common Computed Tomography Examinations and the Associated Lifetime Attributable Risk of Cancer
    WEB-ONLY CONTENT Radiation Dose Associated With Common Computed Tomography Examinations and the Associated Lifetime Attributable Risk of Cancer Rebecca Smith-Bindman, MD; Jafi Lipson, MD; Ralph Marcus, BA; Kwang-Pyo Kim, PhD; Mahadevappa Mahesh, MS, PhD; Robert Gould, ScD; Amy Berrington de Gonza´lez, DPhil; Diana L. Miglioretti, PhD Arch Intern Med. 2009;169(22):2078-2086 DOSIMETRY QUANTITIES defined as joules per kilogram. The unit of gray can be used AND GLOSSARY OF TERMS for any type of radiation, but it does not describe the bio- logical effects of different types of radiation. When radiation interacts with biological matter, the re- Radiation Weighting Factor: A dimensionless factor sulting biological effect depends on the amount of ra- by which the organ absorbed dose (rad or gray) is mul- diation energy absorbed into the material and the type tiplied to obtain a quantity that expresses, on a common of radiation. Organ dose or organ-specific absorbed dose scale for all ionizing radiation, the biological damage (rem is defined as the energy imparted per unit mass of an or- or sievert) to an exposed person. It is used because some gan or tissue. The “absorbed dose” is measured in grays types of radiation, such as alpha particles, are more bio- (Gy), defined as joules per kilogram. The gray replaced logically damaging internally than others. It is used to the rad (radiation absorbed dose), the traditional unit of derive the equivalent dose from the absorbed dose aver- absorbed dose, which is equal to 0.01 Gy. aged over a tissue or organ.
    [Show full text]
  • Risk of Acute Radiation Syndromes Due to Solar Particle Events
    Evidence Report: Risk of Acute Radiation Syndromes due to Solar Particle Events Human Research Program Space Radiation Program Element Approved for Public Release: April 6, 2016 National Aeronautics and Space Administration Lyndon B. Johnson Space Center Houston, Texas CURRENT CONTRIBUTING AUTHORS: Lisa Carnell, PhD NASA Langley Research Center, Hampton, VA Steve Blattnig, PhD NASA Langley Research Center, Hampton, VA Shaowen Hu, PhD Wyle Science Technology & Engineering, Houston, TX Janice Huff, PhD Universities Space Research Association, Houston, TX Myung-Hee Kim, PhD Wyle Science Technology & Engineering, Houston, TX Ryan Norman, PhD NASA Langley Research Center, Hampton, VA Zarana Patel, PhD Wyle Science Technology & Engineering, Houston, TX Lisa Simonsen, PhD NASA Langley Research Center, Hampton, VA Honglu Wu, PhD NASA Johnson Space Center, Houston, TX PREVIOUS CONTRIBUTING AUTHORS: Honglu Wu NASA Johnson Space Center Janice L. Huff Universities Space Research Association Rachel Casey Universities Space Research Association Myung-Hee Kim Universities Space Research Association Francis A. Cucinotta NASA Johnson Space Center Reference for original report: Human Health and Performance Risks of Space Exploration Missions, (Jancy C. McPhee and John B. Charles, editors), NASA SP-2009- 3405, 2009. 1 Table of Contents I. PRD RISK TITLE: RISK OF ACUTE RADIATION SYNDROMES DUE TO SOLAR PARTICLE EVENTS ........................................................................................... 4 II. EXECUTIVE SUMMARY ................................................................................................
    [Show full text]
  • Cavity Theory with Corrections
    CitThCavity Theory, Stopping -Power Ratios, Correction Factors. Alan E. Nahum PhD Physics Department Clatterbridge Centre for Oncology Bebington, Wirral CH63 4JY UK ((@[email protected]) AAPM Summer School, CLINICAL DOSIMETRY FOR RADIOTHERAPY, 21-25 June 2009, Colorado College, Colorado Springs, USA 1 A. E. Nahum: Cavity Theory, Stopping-Power Ratios, Correction Factors. 313.1 INTRODUCTION 3.2 “LARGE” PHOTON DETECTORS 3.3 BRAGG-GRAY CAVITY THEORY 3.4 STOPPING-POWER RATIOS 3.5 THICK-WALLED ION CHAMBERS 363.6 CORRECTION OR PERTURBATION FACTORS FOR ION CHAMBERS 373.7 GENERAL CAVITY THEORY 3.8 PRACTICAL DETECTORS 3.9 SUMMARY 2 A. E. Nahum: Cavity Theory, Stopping-Power Ratios, Correction Factors. Accurate knowledgg(p)e of the (patient) dose in radiation therapy is crucial to clinical outcome For a given fraction size 100 TCP 80 (%) 60 Therapeutic Ratio NTCP 40 & NTCP 20 TCP 0 20 40 60Dpr 80 100 Dose (Gy) 3 A. E. Nahum: Cavity Theory, Stopping-Power Ratios, Correction Factors. Detectors almost never measure dose to medium directly. Therefore, the interpretation of detector reading requires dosimetry theory - “cavity theory” 4 A. E. Nahum: Cavity Theory, Stopping-Power Ratios, Correction Factors. D especially when converting med from calibration at Q to f Q 1 D measurement at Q2 5 det Q A. E. Nahum: Cavity Theory, Stopping-Power Ratios, Correction Factors. Also the “physics” of depth-dose curves: 6 A. E. Nahum: Cavity Theory, Stopping-Power Ratios, Correction Factors. Dose computation in a TPS Terma cfKf. Kerma 7 First we will remind ourselves of two key results which relate the particle fluence, , to energy deposition in the medium.
    [Show full text]
  • Acute Radiation Syndrome: a Fact Sheet for Physicians
    FACT SHEET Acute Radiation Syndrome: A Fact Sheet for Physicians Acute Radiation Syndrome (ARS) (sometimes known as radiation toxicity or radiation sickness) is an acute illness caused by irradiation of the entire body (or most of the body) by a high dose of penetrating radiation in a very short period of time (usually a matter of minutes). The major cause of this syndrome is depletion of immature parenchymal stem cells in specific tissues. Examples of people who suffered from ARS are the survivors of the Hiroshima and Nagasaki atomic bombs, the firefighters that first responded after the Chernobyl Nuclear Power Plant event in 1986, and some unintentional exposures to sterilization irradiators. The required conditions for Acute Radiation Syndrome (ARS) are: • The radiation dose must be large (i.e., greater than 0.7 Gray (Gy)1,2 or 70 rads). o Mild symptoms may be observed with doses as low as 0.3 Gy or 30 rads. • The dose usually must be external (i.e., the source of radiation is outside of the patient’s body). o Radioactive materials deposited inside the body have produced some ARS effects only in extremely rare cases. • The radiation must be penetrating (i.e., able to reach the internal organs). o High energy X-rays, gamma rays, and neutrons are penetrating radiations. • The entire body (or a significant portion of it) must have received the dose.3 o Most radiation injuries are local, frequently involving the hands, and these local injuries seldom cause classical signs of ARS. • The dose must have been delivered in a short time (usually a matter of minutes).
    [Show full text]
  • Bq = Becquerel Gy = Gray (Sv = Sievert)
    Louis Harold Gray He is honored by call- ing the physical dose Bq = becquerel unit "gray*" – abbrevi- Gy = gray ated Gy (Sv = sievert) Photo from 1957 Chapter 5 Activity and Dose The activity of a radioactive source When an atom disintegrates, radiation is emitted. If the rate of disintegrations is large, the radioactive source is considered to have a high activity. The unit for the activity of a radioactive source was named after Becquerel (abbreviated Bq) and is defined as: 1 Bq = 1 disintegration per sec. In a number of countries, the old unit, the curie (abbreviated Ci and named after Marie and Pierre Curie) is still used. The curie-unit was defined as the activity in one gram of radium. The number of disintegrations per second in one gram of radium is 37 billion. The relation between the curie and the becquerel is given by: 1 Ci = 3.7 • 1010 Bq The accepted practice is to give the activity of a radioactive source in becquerel. This is because Bq is the unit chosen for the system of international units (SI-units). But one problem is that the numbers in becquerel are always very large. Consequently the activity is given in kilo (103), mega (106), giga (109)and tera (1012) becquerel. If a source is given in curies the number is small. For example; when talking about radioactivity in food products, 3,700 Bq per kilogram of meat is a large number and consequently considered to be dangerous. If however, the same activity is given in Ci, it is only 0.0000001 curie per kilogram – "nothing to worry about?".
    [Show full text]