Presentation of Finite Dimensions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Disability Classification System
CLASSIFICATION SYSTEM FOR STUDENTS WITH A DISABILITY Track & Field (NB: also used for Cross Country where applicable) Current Previous Definition Classification Classification Deaf (Track & Field Events) T/F 01 HI 55db loss on the average at 500, 1000 and 2000Hz in the better Equivalent to Au2 ear Visually Impaired T/F 11 B1 From no light perception at all in either eye, up to and including the ability to perceive light; inability to recognise objects or contours in any direction and at any distance. T/F 12 B2 Ability to recognise objects up to a distance of 2 metres ie below 2/60 and/or visual field of less than five (5) degrees. T/F13 B3 Can recognise contours between 2 and 6 metres away ie 2/60- 6/60 and visual field of more than five (5) degrees and less than twenty (20) degrees. Intellectually Disabled T/F 20 ID Intellectually disabled. The athlete’s intellectual functioning is 75 or below. Limitations in two or more of the following adaptive skill areas; communication, self-care; home living, social skills, community use, self direction, health and safety, functional academics, leisure and work. They must have acquired their condition before age 18. Cerebral Palsy C2 Upper Severe to moderate quadriplegia. Upper extremity events are Wheelchair performed by pushing the wheelchair with one or two arms and the wheelchair propulsion is restricted due to poor control. Upper extremity athletes have limited control of movements, but are able to produce some semblance of throwing motion. T/F 33 C3 Wheelchair Moderate quadriplegia. Fair functional strength and moderate problems in upper extremities and torso. -

Ifds Functional Classification System & Procedures
IFDS FUNCTIONAL CLASSIFICATION SYSTEM & PROCEDURES MANUAL 2009 - 2012 Effective – 1 January 2009 Originally Published – March 2009 IFDS, C/o ISAF UK Ltd, Ariadne House, Town Quay, Southampton, Hampshire, SO14 2AQ, GREAT BRITAIN Tel. +44 2380 635111 Fax. +44 2380 635789 Email: [email protected] Web: www.sailing.org/disabled 1 Contents Page Introduction 5 Part A – Functional Classification System Rules for Sailors A1 General Overview and Sailor Evaluation 6 A1.1 Purpose 6 A1.2 Sailing Functions 6 A1.3 Ranking of Functional Limitations 6 A1.4 Eligibility for Competition 6 A1.5 Minimum Disability 7 A2 IFDS Class and Status 8 A2.1 Class 8 A2.2 Class Status 8 A2.3 Master List 10 A3 Classification Procedure 10 A3.0 Classification Administration Fee 10 A3.1 Personal Assistive Devices 10 A3.2 Medical Documentation 11 A3.3 Sailors’ Responsibility for Classification Evaluation 11 A3.4 Sailor Presentation for Classification Evaluation 12 A3.5 Method of Assessment 12 A3.6 Deciding the Class 14 A4 Failure to attend/Non Co-operation/Misrepresentation 16 A4.1 Sailor Failure to Attend Evaluation 16 A4.2 Non Co-operation during Evaluation 16 A4.3 International Misrepresentation of Skills and/or Abilities 17 A4.4 Consequences for Sailor Support Personnel 18 A4.5 Consequences for Teams 18 A5 Specific Rules for Boat Classes 18 A5.1 Paralympic Boat Classes 18 A5.2 Non-Paralympic Boat Classes 19 Part B – Protest and Appeals B1 Protest 20 B1.1 General Principles 20 B1.2 Class Status and Protest Opportunities 21 B1.3 Parties who may submit a Classification Protest -

Recursive Syntactic Pattern Learning by Songbirds
Recursive syntactic pattern learning by songbirds Timothy Q. Gentner, Kimberly M. Fenn, Daniel Margoliash, and Howard C. Nusbaum Supplementary Information Table S1 provides an overview of all the training and testing conditions. Condition Stimulus 1 Baseline Training A2B2 and (AB)2, n=2 2 Transfer 1 Novel A2B2 and (AB)2, n=2 3 Probe Test 1 Familiar A2B2 and (AB)2, n=2 (80% of trials) Novel A2B2 and (AB)2, n=2 (10% of trials) Agrammatical AAAA, BBBB, ABBA, BAAB (10% of trials) 4 Probe Test 2 Familiar A2B2 and (AB)2, n=2 (80% of trials) Novel AnBn and (AB)n, n=3, 4 (20% of trials) 5 Probe Test 3 Familiar A2B2 and (AB)2, n=2 (80% of trials) A*B* (10% of trials) Novel AnBn and (AB)n, n=2,3,4 (10% of trials) Table S1. Overview of the training and testing conditions in order to which subjects were exposed. Stimuli marked with (*) comprised speech syllables instead of starling song motifs. Probe tests with novel A2B2 and (AB)2 stimuli Because the novel transfer stimuli were reinforced with the same response contingencies used in the initial training, the animals’ behaviour was changing (i.e. they were learning) as we measured generalization. To examine generalization without contingent reinforcement and thus without additional learning, we tested subjects using a “probe” procedure. The reinforcement regimen during probe sessions allowed us to measure generalization from the classes defined by the familiar CFG and FSG stimuli to novel stimuli without any direct effects of differential reinforcement learning on the latter (see Additional Methods). -

GAMES OFFICIALS' GUIDE Equestrian
GAMES OFFICIALS' GUIDE Equestrian July 2021 © The Tokyo Organising Committee of the Olympic and Paralympic Games 21SPT1599000 About this Games Officials’ Guide Published in July 2021, the series of Games Officials’ Guides offer a summary of competition-related material about each sport at the Tokyo 2020 Paralympic Games and provide a variety of information aimed at helping International Federations and their technical officials and classifiers plan and prepare for the Games. All information provided in this Games Officials’ Guide was correct at the time of publication, but some details may change prior to the Games so stakeholders are urged to regularly check with Tokyo 2020 IF Services department and the respective Tokyo 2020 competition management teams for the latest updates. Regarding COVID-19 protocols, updated versions of 'The Playbook International Federations' will be attached to the Games Officials' Guides, and sport-specific COVID-19 countermeasures approved by International Federations and Tokyo 2020 competition management will be made available. The Games Officials’ Guides are designed for internal operational use by Tokyo 2020 stakeholders and should not be publicly shared. Equestrian - Games Officials’ Guide 02 WELCOME On behalf of the Tokyo Organising Committee of the Olympic and Paralympic Games, I am delighted to present the Equestrian Games Officials’ Guide for the Tokyo 2020 Paralympic Games. We have been working diligently to provide facilities, services and procedures which will allow everyone involved in the Games to safely achieve all three of Tokyo 2020’s core concepts: achieving personals bests, unity in diversity, and connecting to tomorrow. Included is information about: • processes relating to competition • key dates and personnel • competition format and rules • venue facilities and services, including maps • information about COVID-19 protocols, heat countermeasures, accreditation, accommodation, Games- time medical services, etc. -

Materials and Welding
Rules for Materials and Welding Part 2 July 2021 RULES FOR MATERIALS AND WELDING JULY 2021 PART 2 American Bureau of Shipping Incorporated by Act of Legislature of the State of New York 1862 © 2021 American Bureau of Shipping. All rights reserved. ABS Plaza 1701 City Plaza Drive Spring, TX 77389 USA PART 2 Foreword (1 July 2021) For the 1996 edition, the “Rules for Building and Classing Steel Vessels – Part 2: Materials and Welding” was re-titled “Rule Requirements for Materials and Welding (Part 2).” The purpose of this generic title was to emphasize the common applicability of the material and welding requirements in “Part 2” to ABS classed vessels, other marine structures and their associated machinery, and thereby make “Part 2” more readily a common “Part” of the various ABS Rules and Guides, as appropriate. Accordingly, the subject booklet, Rules for Materials and Welding (Part 2), is to be considered, for example, as being applicable and comprising a “Part” of the following ABS Rules and Guides: ● Rules for Building and Classing Marine Vessels ● Rules for Building and Classing Steel Vessels for Service on Rivers and Intracoastal Waterways ● Rules for Building and Classing Mobile Offshore Units ● Rules for Building and Classing Steel Barges ● Rules for Building and Classing High-Speed Craft ● Rules for Building and Classing Floating Production Installations ● Rules for Building and Classing Light Warships, Patrol and High-Speed Naval Vessels ● Guide for Building and Classing Liftboats ● Guide for Building and Classing International Naval Ships ● Guide for Building and Classing Yachts In the 2002 edition, Section 4, “Piping” was added to Part 2, Chapter 4, “Welding and Fabrication”. -

Nebraska Highway 12 Niobrara East & West
WWelcomeelcome Nebraska Highway 12 Niobrara East & West Draft Environmental Impact Statement and Section 404 Permit Application Public Open House and Public Hearing PPurposeurpose & NNeedeed What is the purpose of the N-12 project? - Provide a reliable roadway - Safely accommodate current and future traffi c levels - Maintain regional traffi c connectivity Why is the N-12 project needed? - Driven by fl ooding - Unreliable roadway, safety concerns, and interruption in regional traffi c connectivity Photo at top: N-12 with no paved shoulder and narrow lane widths Photo at bottom: Maintenance occurring on N-12 PProjectroject RRolesoles Tribal*/Public NDOR (Applicant) Agencies & County Corps » Provide additional or » Respond to the Corps’ » Provide technical input » Comply with Clean new information requests for information and consultation Water Act » Provide new reasonable » Develop and submit » Make the Section 7(a) » Comply with National alternatives a Section 404 permit decision (National Park Service) Environmental Policy Act application » Question accuracy and » Approvals and reviews » Conduct tribal adequacy of information » Planning, design, and that adhere to federal, consultation construction of Applied- state, or local laws and » Coordinate with NDOR, for Project requirements agencies, and public » Implementation of » Make a decision mitigation on NDOR’s permit application * Conducted through government-to-government consultation. AApplied-forpplied-for PProjectroject (Alternative A7 - Base of Bluff s Elevated Alignment) Attribute -

Local Law 152 of 2016: Inspections of Exposed Gas Piping Faqs
September 2020 FREQUENTLY ASKED QUESTIONS LocalJune Law2010 152 of 2016: Inspections of Exposed Gas Piping INSPECTIONS GENERALLY Q1. This inspection is a point in time inspection of a gas system. Assuming the inspection was conducted properly, at what point does the inspector’s liability end? A1. The licensee is responsible for the work performed and the accuracy of any forms completed and submitted to the owner and the Department. Q2. Is it required to prove the legality of an existing gas installation? A2. While the licensee is not required to prove legality of an existing gas installation, the licensee is responsible for identifying illegal connections or any non-Code compliant conditions. Q3. Does the inspection requirement include commercial spaces? A3. The inspection requirement applies to all buildings other than R-3 (ex. 1 & 2 family). The law outlines the scope of the inspection, starting at the point of entry into the building and up to, but not including tenant space. Tenant spaces are not included in the scope, regardless of their occupancy classification. Q4. If there is a boiler room or mechanical room in a tenant space, is it exempt from the inspection and leak survey? A4. Yes, if there is a boiler room or mechanical room in a tenant space, it is exempt from the inspection and leak survey. Q5. Are there any circumstances under which an appliance within any tenant space will be subject to an inspection or survey? A5. No. Appliances within tenant spaces are not subject to an inspection or survey. Q6. What actions must the plumber take if access is not available to all required areas containing the exposed gas piping for the visual inspection or if access is not provided to public spaces, hallways, corridors, and mechanical and boiler rooms for the leak survey? A6. -

Document Owner Suela Kodra Data Classification Confidential
Document Classification: Public Statement of Applicability, Version 2.0, 4 May 2021 Legend for Reasons for Controls Selection LR: Legal Requirements,CO: Contractual Obligations,BR/BP: Business Requirements/Adopted Best Practices,RRA: Results of Risk Assessment Section Information security control Reference Applicable A5 Information security policies A5.1 Management direction for information security Information_Security_Policy; ISMS Yes A5.1.1 Policies for information security Manual; Security Concept A5.1.2 Review of the policies for information security Document_and_Policy Management Yes A6 Organization of information security A6.1 Internal organization ISMS Manual; Information_Security_Policy; Job Yes A6.1.1 Information security roles and responsibilities descriptions ISMS Manual; Information_Security_Policy; Yes A6.1.2 Segregation of duties Access_Control_Policy Computer_Security_Incident_Respon Yes A6.1.3 Contact with authorities se_Plan (Annex II) Computer_Security_Incident_Respon Yes A6.1.4 Contact with special interest groups se_Plan (Annex II) Information Security Risk Management Policy; Software Yes A6.1.5 Information security in project management Development Process A6.2 Mobile devices and teleworking A6.2.1 Mobile device policy Mobile_Device_Policy Yes A6.2.2 Teleworking Teleworking_Policy Yes A7 Human resource security A7.1 Prior to employment A7.1.1 Screening On_Off Boarding Checkliste Yes A7.1.2 Terms and conditions of employment Safety io Arbeitsvertrag_AT Yes A7.2 During employment Information_Security_Policy; ISMS Yes -

Environmental Impact Statement Volume I Part A
un,ted Stat- DepW’tment 01 Agriculture Forest SerVlCe NOrthem Region --. - _ “rO,lno, l”llll” Clearwater NatisnaB Fsaest September, 1987 J3NVIRONMFNlXLIMPACT STATEMENT of the CLRARWATERNATIONAL FOREST LANDANDRESOURCEMANAGEMENTPLAN September 1987 Benewah, Clearwater, Idaho, Lewis, Nez Perce, L&ah. and Shoshone Counties in Idaho Responsible Agency: USDA, Forest Servxe Responsible Official: James C. Overbay, Regional Forester USDA Forest Service Northern Region Federal Building. PO Box 7669 Missoula, Montana 59807 For Further Information Contact: James C. Bates Forest Supervisor Clearwater National Forest 12730 HIghway 12 Orofino, Idaho 83544 (208) 476-4541 This Environmental Impact Statement describes the Preferred Alternative and eleven alternatives. including the "current directIon" alternative for managing the 1.8 million acres of the Clearwater Natxonal Forest. The twelve alternatlves provide different mixes of management activities resulting in different levels of outputs, goods, and services. The environmental consequences for all the alternatlves are displayed. TABLE OF CONTENTS SuMMARY...............................S- 1 I. PURPOSEANDNEED........................ I-l A. Introductxon. ........................ I-l B. NatLonal, RegIonal, and Forest Planning ........... I-l C. Forest LocatIon ....................... I-4 D. Issues, Concerns, and Opportunltles ............. I-4 E. Changes Between the Draft and FInal EnvIronmental Impact Statement. ........... 1-8 F. Reader's Guide. ....................... I-10 II. ALTERNATIVES.......................... -

US SAILING FUNCTIONAL CLASSIFICATION SYSTEM & PROCEDURES MANUAL 2013—2016 Effective—1 January 2013
[Type text ] [Type text ] [Type text ] US SAILING FUNCTIONAL CLASSIFICATION SYSTEM & PROCEDURES MANUAL 2013—2016 Effective—1 January 2013 Originally Published—May 2013 US Sailing Member of the PO Box 1260 15 Maritime Drive Portsmouth, RI 02871-0907 Phone: 1-401-683-0800 / Toll free: 1-800-USSAIL - (1-800-877-2451) Fax: 401-683-0840 E-Mail: [email protected] International Paralympic Committee Roger H S trube, MD – A pril 20 13 1 ROGE R H STRUBE, MD – APRIL 2013 [Type text ] [Type text ] [Type text ] Contents Introduction .................................................................................................................................................... 6 Appendix to Introduction – Glossary of Medical Terminology .......................................................................... 7 Joint Movement Definitions: ........................................................................................................................... 7 Neck ........................................................................................................................................................ 7 Shoulder .................................................................................................................................................. 7 Elbow ...................................................................................................................................................... 7 Wrist ...................................................................................................................................................... -
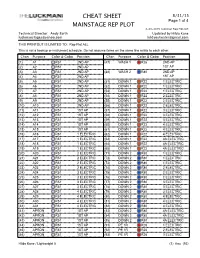
8-28-2015 Luckman Rep Plot.Lw5 Technical Director: Andy Barth Updated by Hilda Kane [email protected] [email protected]
CHEAT SHEET 8/31/15 Page 1 of 4 MAINSTAGE REP PLOT 8-28-2015 Luckman Rep Plot.lw5 Technical Director: Andy Barth Updated by Hilda Kane [email protected] [email protected] THIS PRINTOUT IS LIMITED TO: Rep Plot ALL This is not a hookup or instrument schedule. Do not assume items on the same line relate to each other. Chan Purpose Color & Gobo Position Chan Purpose Color & Gobo Position (1) A1 R51 2ND AP (47) WASH 1 R26 2ND AP (2) A2 R51 2ND AP 1ST AP (3) A3 R51 2ND AP (48) WASH 2 R80 2ND AP (4) A4 R51 2ND AP 1ST AP (5) A5 R51 2ND AP (51) DOWN 1 R22 1 ELECTRIC (6) A6 R51 2ND AP (52) DOWN 1 R22 1 ELECTRIC (7) A7 R51 2ND AP (53) DOWN 1 R22 1 ELECTRIC (8) A8 R51 2ND AP (54) DOWN 1 R22 2 ELECTRIC (9) A9 R51 2ND AP (55) DOWN 1 R22 2 ELECTRIC (10) A10 R51 2ND AP (56) DOWN 1 R22 2 ELECTRIC (11) A11 R51 1ST AP (57) DOWN 1 R22 3 ELECTRIC (12) A12 R51 1ST AP (58) DOWN 1 R22 3 ELECTRIC (13) A13 R51 1ST AP (59) DOWN 1 R22 3 ELECTRIC (14) A14 R51 1ST AP (60) DOWN 1 R22 4 ELECTRIC (15) A15 R51 1ST AP (61) DOWN 1 R22 4 ELECTRIC (16) A16 R51 1 ELECTRIC (62) DOWN 1 R22 4 ELECTRIC (17) A17 R51 1 ELECTRIC (63) DOWN 1 R22 4A ELECTRIC (18) A18 R51 1 ELECTRIC (64) DOWN 1 R22 4A ELECTRIC (19) A19 R51 1 ELECTRIC (65) DOWN 1 R22 4A ELECTRIC (20) A20 R51 2 ELECTRIC (71) DOWN 2 R80 1 ELECTRIC (21) A21 R51 2 ELECTRIC (72) DOWN 2 R80 1 ELECTRIC (22) A22 R51 2 ELECTRIC (73) DOWN 2 R80 1 ELECTRIC (23) A23 R51 2 ELECTRIC (74) DOWN 2 R80 2 ELECTRIC (24) A24 R51 3 ELECTRIC (75) DOWN 2 R80 2 ELECTRIC (25) A25 R51 3 ELECTRIC (76) DOWN 2 R80 2 ELECTRIC (26) A26 R51 3 ELECTRIC (77) DOWN 2 R80 3 ELECTRIC (27) A27 R51 3 ELECTRIC (78) DOWN 2 R80 3 ELECTRIC (28) A28 R51 4 ELECTRIC (79) DOWN 2 R80 3 ELECTRIC (29) A29 R51 4 ELECTRIC (80) DOWN 2 R80 4 ELECTRIC (30) A30 R51 4 ELECTRIC (81) DOWN 2 R80 4 ELECTRIC (31) A31 R51 4 ELECTRIC (82) DOWN 2 R80 4 ELECTRIC (41) APRON R51 1ST AP (83) DOWN 2 R80 4A ELECTRIC (42) APRON .. -

Specification for Welding Shielding Gases
ANSI/AWS A5.32/A5.32M-97 An American National Standard Specification for Welding Shielding Gases Key Words— Argon, carbon dioxide, helium, ANSI/AWS A5.32/A5.32M-97 hydrogen, nitrogen, oxygen, shielding An American National Standard gases, welding gases Approved by American National Standards Institute December 8, 1997 Specification for Welding Shielding Gases Prepared by AWS Committee on Filler Metals Under the Direction of AWS Technical Activities Committee Approved by AWS Board of Directors Abstract This specification for welding shielding gases specifies minimum requirements for the composition and purity of the most popular single-component shielding gases. Classification designators for both single and multicomponent gases are introduced. Other topics include testing procedures, package marking, and general application guidelines. This specification makes use of both U.S. Customary Units and the International System of Units (SI). Since these are not equivalent, each system must be used independently of the other. 550 N.W. LeJeune Road, Miami, Florida 33126 Table of Contents Page No. Personnel.................................................................................................................................................................... iii Foreword ................................................................................................................................................................... v List of Tables ..............................................................................................................................................................vii