DOCSLIB.ORG

Characterization of Accommodation Response in Foveated Near-Eye Holographic Displays

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Characterization of Accommodation Response in Foveated Near-Eye Holographic Displays CHARACTERIZATION OF ACCOMMODATION RESPONSE IN FOVEATED NEAR-EYE HOLOGRAPHIC DISPLAYS Jani Makinen,¨ Erdem Sahin, Atanas Gotchev Faculty of Information Technology and Communication Sciences, Tampere University, Finland ABSTRACT analysis considered only ray-based optics. As a result, there is Foveation is an extremely powerful tool for reducing computa- an apparent need for accurate analysis and simulation of human tional burden in near-eye displays. Applying such methods for dis- vision for wave optics based applications. plays capable of producing the majority of 3D visual cues, how- In this paper, we analyze the accommodation response of the ever, requires accurate models and knowledge of the human visual HVS for a near-eye holographic display. To improve the accuracy perception to exploit its weaknesses effectively. Spatial resolution of the HVS model, a non-uniform sampling scheme is adopted, is the main concern in regular 2D displays, whereas in the case based on the density of the human retinal ganglion cell receptive of 3D displays additional visual cues, such as accommodation, re- field [7]. Additionally, the simulations include the curvature of the quire attention. This paper analyzes such cues for near-eye holo- retina. The approach for simulating the viewing process of the hu- graphic displays by considering the perceptual properties of the man eye utilizes numerical wavefield propagation. We analyze the human vision, particularly the visual acuity relative to the gaze di- accommodation response via point spread functions (PSF) as well rection. We develop a numerical wave optics based reconstruction as the modulation transfer functions (MTF) from the perceived tool incorporating a perceptual model of the human eye to simu- retinal images. The response is evaluated as a function of eccen- late the natural viewing process with high accuracy. Based on our tricity by changing the position of the displayed content relative analysis, general guidelines are found regarding the accuracy of to the gaze horizontally. Thus, we find the accuracy of the ac- the accommodation cues relative to the gaze of the viewer. More commodation cues needed to be provided by the hologram in the importantly, the developed method can be included into the de- peripheral vision. sign process of near-eye holographic displays to computationally optimize their parameters and the foveated rendering techniques. 2. METHOD 2.1. Computational human eye model Index Terms — Holography, near-eye displays, foveation, perceptual modeling, wave optics Near-eye foveated displays take advantage of the shortcomings of the HVS and rely on models to provide the necessary information 1. INTRODUCTION regarding e.g. sampling and rendering budget. Such models can also be incorporated into simulation tools designed to mimic the Holographic displays, despite their ability to replicate 3D content visual process of a human eye. In general, these simulation tools highly realistically, have not yet seen widespread use due to the consider the human eye as a camera with a thin lens, where the extremely demanding computational requirements to achieve full lens is equivalent to the pupil and the sensor to the retina. This parallax and a wide viewing angle. By restricting the position configuration defines three parallel planes: display (or hologram), of the viewer near to the display, as done in near-eye displays lens and sensor. Each plane needs to be discretely sampled ac- [1, 2, 3], the limitations of the human visual system in addition cording their corresponding sampling requirements for numerical to the restricted position can be exploited to relieve the display re- simulations, which is typically done in a uniform fashion. Here quirements, such as viewing angle. Moreover, in such displays the we will describe how to improve the human eye model, specifi- gaze of the viewer can be more easily tracked, thus allowing for cally targeting the sampling of the sensor plane. foveated rendering methods to further optimize the computations. A key part of an accurate perceptual model of the human vi- For this purpose, it is important not only to know the perceptual sion is the decrease of visual acuity (away from gaze). Here we limits of human vision, such as the spatial resolution and accom- adopt the model proposed in [7] describing the density of the reti- modation response, but also to be able to accurately simulate the nal ganglion cell receptive field as a function of retinal eccentricity viewing process of the human eye. r = px2 + y2 and meridian m Previous research on characterizing the properties of 3D dis- plays in relation to visual perception mainly considered ray-based r −1 ρ(r; m) = 2ρ 1 + light field (LF) displays [4]. In an effort to extend the analysis to cone 41:03 holographic stereograms (HS), our previous work [5] employed " # r −2 r wave optics based numerical viewing simulations. In these simu- × am 1 + + (1 − am) exp : (1) lations the human eye is considered as a camera with a thin lens r2;m re;m for the pupil and a flat uniformly sampled sensor for the retina. However, more accurate analysis and models are needed specifi- The constants ρcone, am, r2;m, re;m fit the model along the four cally for near-eye applications. A more precise model of the hu- different meridians (temporal, superior, nasal, inferior) [7]. The man visual system (HVS) was utilized in [6], where an importance sampling of the retina (in angle) is then defined from the density as [7] sampling model was developed based on the spatial resolution de- s crease away from the visual axis. However, the eye was still ap- 1 2 x2 y2 σ(x; y) = p + : (2) proximated by a flat two-plane parametrization. Moreover, the r 3 ρ(r; 1) ρ(r; 2) Thus, the visual acuity drop-off is modeled by non-uniformly sam- k = 2π/λ is the wave number. Due to the viewing conditions of pling the retinal surface in further steps of the analysis. the near-eye display setup, i.e. short viewing distance and station- Another often overlooked property of the HVS in numerical ary position of the eye, spherical illumination for the hologram is simulations is the curvature of the retina. Though the conventional beneficial to use; it reduces the size of the viewing zone to extend flat two-plane parametrization is an acceptable approximation, the the field-of-view [8]. accuracy of the eye model is improved to some extent by includ- ing the curved parametrization. In this paper, we parametrize the 3. RESULTS AND DISCUSSION retina on a spherical surface with a diameter of l. As a result, the retina is sampled at different z-coordinates based on the eccen- The numerical reconstruction setup for the analysis is presented in tricity. Specifically, a sample at the eccentricity φ on the retina is Fig. 1. That is, a single point source is placed at coordinates (xp, located at distance zu in z-direction from the pupil: zp) and a hologram of it is produced. The hologram is then prop- agated towards the simulated eye at distance zeye, first passing l l zu = + cos φ. (3) through the lens with a transmittance function T (s). The trans- 2 2 mittance function can be modified to focus the eye at different Thus, each sample on the retina has both a horizontal and a depth distances. Finally, the intensity values are retrieved from the retina coordinate. at the positions defined by Eq. 2 and 3. These intensities compose The final part of the computational model is the pupil, which is the perceived PSF for the human eye, from which the MTF is ob- modelled as a thin lens of width D. The 1D transmittance function tained as the magnitude of its spectrum. The MTF describes the T (s) of a thin lens is defined as contrast magnitude across different spatial frequencies. −jπ x s u T (s) = exp s2 ; (4) λf zu point source where λ is the wavelength of the monochromatic light and f is (x , z ) σ(φ) f p p the focal length of the lens. By changing , the lens can be set φ to focus at varying distances, thus providing the ability to evalu- D ate the accommodative properties of the human eye in numerical Δx simulations. 2.2. Numerical simulation via scalar field diffraction zeye l hologram lens sensor In addition to the perceptually accurate eye model, the propagation of light from the display to the eye needs to be modeled. A wave Figure 1. Numerical reconstruction setup for the analysis. optics based approach is adopted here to study the perceived vi- sual properties through numerical simulations. For simplicity, let Let us first consider the behaviour of the MTFs as a function us consider the equations in 1D. The scalar optical field U(ξ; z0) of spatial frequency. For this purpose, the presented numerical is propagated utilizing plane wave decomposition, i.e. for each simulation tool is utilized with the following parameters: the point spatial frequency component f in the field, a plane wave is prop- ξ is set at zp = −50 cm (i.e. 50 cm behind the hologram) and a agated with its corresponding complex amplitude and sampled at Fresnel hologram of it is generated with a sampling step ∆x = 2 the desired secondary positions (x, z). The contributions of each µm, number of samples N = 8192 and wavelength λ = 534 nm. plane wave are combined to obtain the total field U(x; z) as The location of the eye and the pupil size are fixed to zeye = 2 cm Z and D = 5 mm, respectively. The simulated eye is set to focus U(x; z) = FfU(ξ; z0)g(fξ) at the exact distance of the point source, as well as around it at various shifted depths.
Load more

Recommended publications
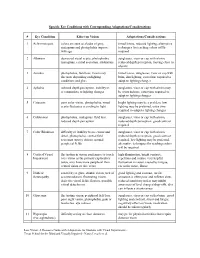
  • Specific Eye Conditions with Corresponding Adaptations/Considerations
    Specific Eye Conditions with Corresponding Adaptations/Considerations # Eye Condition Effect on Vision Adaptations/Considerations 1 Achromotopsia colors are seen as shades of grey, tinted lenses, reduced lighting, alternative nystagmus and photophobia improve techniques for teaching colors will be with age required 2 Albinism decreased visual acuity, photophobia, sunglasses, visor or cap with a brim, nystagmus, central scotomas, strabismus reduced depth perception, moving close to objects 3 Aniridia photophobia, field loss, vision may tinted lenses, sunglasses, visor or cap with fluctuate depending on lighting brim, dim lighting, extra time required to conditions and glare adapt to lighting changes 4 Aphakia reduced depth perception, inability to sunglasses, visor or cap with a brim may accommodate to lighting changes be worn indoors, extra time required to adapt to lighting changes 5 Cataracts poor color vision, photophobia, visual bright lighting may be a problem, low acuity fluctuates according to light lighting may be preferred, extra time required to adapt to lighting changes 6 Colobomas photophobia, nystagmus, field loss, sunglasses, visor or cap with a brim, reduced depth perception reduced depth perception, good contrast required 7 Color Blindness difficulty or inability to see colors and sunglasses, visor or cap with a brim, detail, photophobia, central field reduced depth perception, good contrast scotomas (spotty vision), normal required, low lighting may be preferred, peripheral fields alternative techniques for teaching colors
    [Show full text]
  • Two Eyes See More Than One Human Beings Have Two Eyes Located About 6 Cm (About 2.4 In.) Apart
    ivi act ty 2 TTwowo EyesEyes SeeSee MoreMore ThanThan OneOne OBJECTIVES 1 straw 1 card, index (cut in half widthwise) Students discover how having two eyes helps us see in three dimensions and 3 pennies* increases our field of vision. 1 ruler, metric* The students For the class discover that each eye sees objects from a 1 roll string slightly different viewpoint to give us depth 1 roll tape, masking perception 1 pair scissors* observe that depth perception decreases *provided by the teacher with the use of just one eye measure their field of vision observe that their field of vision decreases PREPARATION with the use of just one eye Session I 1 Make a copy of Activity Sheet 2, Part A, for each student. SCHEDULE 2 Each team of two will need a metric ruler, Session I About 30 minutes three paper cups, and three pennies. Session II About 40 minutes Students will either close or cover their eyes, or you may use blindfolds. (Students should use their own blindfold—a bandanna or long strip VOCABULARY of cloth brought from home and stored in their science journals for use—in this depth perception and other activities.) field of vision peripheral vision Session II 1 Make a copy of Activity Sheet 2, Part B, for each student. MATERIALS 2 For each team, cut a length of string 50 cm (about 20 in.) long. Cut enough index For each student cards in half (widthwise) to give each team 1 Activity Sheet 2, Parts A and B half a card. Snip the corners of the cards to eliminate sharp edges.
    [Show full text]
  • Binocular Vision
    BINOCULAR VISION Rahul Bhola, MD Pediatric Ophthalmology Fellow The University of Iowa Department of Ophthalmology & Visual Sciences posted Jan. 18, 2006, updated Jan. 23, 2006 Binocular vision is one of the hallmarks of the human race that has bestowed on it the supremacy in the hierarchy of the animal kingdom. It is an asset with normal alignment of the two eyes, but becomes a liability when the alignment is lost. Binocular Single Vision may be defined as the state of simultaneous vision, which is achieved by the coordinated use of both eyes, so that separate and slightly dissimilar images arising in each eye are appreciated as a single image by the process of fusion. Thus binocular vision implies fusion, the blending of sight from the two eyes to form a single percept. Binocular Single Vision can be: 1. Normal – Binocular Single vision can be classified as normal when it is bifoveal and there is no manifest deviation. 2. Anomalous - Binocular Single vision is anomalous when the images of the fixated object are projected from the fovea of one eye and an extrafoveal area of the other eye i.e. when the visual direction of the retinal elements has changed. A small manifest strabismus is therefore always present in anomalous Binocular Single vision. Normal Binocular Single vision requires: 1. Clear Visual Axis leading to a reasonably clear vision in both eyes 2. The ability of the retino-cortical elements to function in association with each other to promote the fusion of two slightly dissimilar images i.e. Sensory fusion. 3. The precise co-ordination of the two eyes for all direction of gazes, so that corresponding retino-cortical element are placed in a position to deal with two images i.e.
    [Show full text]
  • Collaborative Treatment for Vision After TBI
    Collaborative Treatment for Vision After TBI Tom Wilson, OD, COVD Terri Cassidy, OTR, CDRS Vision is Primary • Human vision is a complex process that involves the coordinated efforts of both the eyes and the brain. • We use central vision (focal) to see detail. • We use peripheral vision (ambient) to inform us of movement or a direction we should point our eyes. • Even if we feel like our eyes (and brain) are not giving us accurate information – we believe our eyes. 2 Case Study 1 56 y/o woman involved in a motor vehicle crash. She was able to walk and talk. MRI was negative. Not long after she notices symptoms of not being able to read correctly, headaches, motion sickness is much worse than normal, she can’t go back to work on the computer, she is very tentative about driving. Her eye doctor tells her that her eyes are fine, it must be her medications. Finally she is referred to Dr. Wilson who does an evaluation and refers her to vision rehab with OT. Presentation Title – Date (month #, ####) 3 Evaluation Neuro-optometric Assessment • Eye health • Binocular Vision • Prism evaluation • Function Occupational Therapy Vision Assessment • Goal of OT is to improve the client’s level of performance in a needed ADL. • Deficiencies in visual processing are significant to the OT Process if they interfere with occupational performance – doing the tasks that she wants and needs to do. Presentation Title – Date (month #, ####) 4 Evaluation Results OD Finds: OT Finds: Characteristics of Post Trauma Pt is not able to work more than 2 Vision Syndrome
    [Show full text]
  • 20/20 VISION Part I: Eyesight, Perception and Vision
    20/20 VISION Part I: Eyesight, perception and vision In this first part of our three-part exploration of 20/20 vision, we are going to look at our physical eyes and how they work. Then we will explore perception and how the brain actually converts all that sensory information into images. Finally, we will look at some of the techniques for improving our vision naturally and ask if these really work. 20/20 vision is a term used to express normal visual acuity (the clarity or sharpness of vision) measured at a distance of 20 feet. ... If you have 20/100 vision, it means that you must be as close as 20 feet to see what a person with normal vision can see at 100 feet. Having 20/20 vision does not necessarily mean you have perfect vision. 20/20 vision only indicates the sharpness or clarity of vision at a distance. Other important vision skills, including peripheral awareness or side vision, eye coordination, depth perception, focusing ability and colour vision, contribute to your overall visual ability. Some people can see well at a distance but are unable to bring nearer objects into focus. This condition can be caused by hyperopia (far-sightedness) or presbyopia (loss of focusing ability). Others can see items that are close but cannot see those far away. This condition may be caused by myopia (near-sightedness). Is it possible to see better than 20/20? Yes, it's indeed possible to have sharper than 20/20 vision. In fact, most people with young, healthy eyes are capable of identifying at least some of the letters on the 20/15 line or even smaller letters on the Snellen chart.
    [Show full text]
  • An Adaptive Blur in Peripheral Vision to Reduce Visual Fatigue in Stereoscopic Vision
    ©2016 Society for Imaging Science and Technology DOI: 10.2352/ISSN.2470-1173.2016.5.SDA-438 An Adaptive Blur in Peripheral Vision to Reduce Visual Fatigue in Stereoscopic Vision David AURAT; MINES ParisTech, PSL Research University, Centre for robotics; Paris; France Laure LEROY; Paris 8 University; Saint-Denis; France Olivier HUGUES; MINES ParisTech, PSL Research University, Centre for robotics; Paris; France Philippe FUCHS; MINES ParisTech, PSL Research University, Centre for robotics; Paris; France Abstract Related Work For some years, a lot of Stereoscopic 3D contents have As we described previously, the accommodation ver- been released. Even if the depth sensation is realistic, it gence conflict is a cause of eye strain in stereoscopic 3D is still not perfect and uncomfortable. The objective of our vision. A lot of people have studied this conflict. Some work is to use the gaze of the user to bring closer artificial people created multi-focal system to limits the distance be- vision and natural vision to increase the precision of the per- tween the convergence point and the accommodation point ception and decrease visual fatigue. For example, a differ- like Hoffman et al. [4]. They concluded that multi-focal ence in artificial vision is the accommodation point and the system decrease viewer fatigue and discomfort, increase convergence point of the eye. In natural vision, these points stereoacuity, reduce time to identify a stereo stimulus and are the same whereas in artificial vision event if the con- reduce distortion in perceived depth. Neveu et al. [1] vergence point is on the looked object, the accommodation showed that beginning with a small conflict and increasing point remains on the screen.
    [Show full text]
  • Vision Challenges with Vestibular Disorders
    5018 NE 15TH AVE · PORTLAND, OR 97211 · FAX: (503) 229-8064 · (800) 837-8428 · [email protected] · VESTIBULAR.ORG Vision Challenges with Vestibular Disorders By Michael C. Schubert, PT, PhD with the Vestibular Disorders Association, and contributions by Kenneth Ciuffreda, O.D., PhD, FCOVD-A and Allen H. Cohen, O.D., FCOVD A common complaint for people with patients consult with an optometrist who vestibular disorders is that they have specializes in Neuro-optometric difficulty with their vision. They may Rehabilitation. The neuro-optometric experience problems focusing on an object evaluation specifically assesses the visual, or perceive that objects are moving from ocular motor and focusing skills important side to side or revolving around them for stabilizing the sensory motor (vertigo). They may see their visual field components of the vestibule-ocular reflex jiggle or bounce during head motion (or “VOR”). (oscillopsia) or have double vision (diplo- pia). When they hold their heads still, HOW DO VESTIBULAR DISORDERS these visual instability problems might AFFECT VISION? resolve. The vestibular system and the visual Many people with vestibular disorders system coordinate with each other through consult an eye care professional due to brain pathways in order to control visual their visual symptoms. The typical eye fixation. The ‘ear to eye’ connection is examination is done while the patient’s known as the vestibulo-ocular reflex head is resting against a head rest, (VOR). The VOR has a critical role of thereby reducing the head motion, which keeping the eyes still during head motion. may mask the visual symptoms. With a This is known as gaze stability.
    [Show full text]
  • Effect of Stroboscopic Vision Training on Dynamic Visual Acuity Scores: Nike Vapor Strobe® Eyewear
    Utah State University DigitalCommons@USU All Graduate Plan B and other Reports Graduate Studies 5-2013 Effect of Stroboscopic Vision Training on Dynamic Visual Acuity Scores: Nike Vapor Strobe® Eyewear Joshua Holliday Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/gradreports Recommended Citation Holliday, Joshua, "Effect of Stroboscopic Vision Training on Dynamic Visual Acuity Scores: Nike Vapor Strobe® Eyewear" (2013). All Graduate Plan B and other Reports. 262. https://digitalcommons.usu.edu/gradreports/262 This Report is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Plan B and other Reports by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. Utah State University DigitalCommons@USU All Graduate Plan B and other Reports Graduate Studies 4-2013 Effect of Stroboscopic Vision Training on Dynamic Visual Acuity Scores: Nike Vapor Strobe® Eyewear Joshua Holliday Follow this and additional works at: http://digitalcommons.usu.edu/gradreports Recommended Citation Holliday, Joshua, "Effect of Stroboscopic Vision Training on Dynamic Visual Acuity Scores: Nike Vapor Strobe® Eyewear" (2013). All Graduate Plan B and other Reports. Paper 262. This Report is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Plan B and other Reports by an authorized administrator of DigitalCommons@USU.
    [Show full text]
  • Perceived Speed of Motion in Depth Is Reduced in the Periphery
    Vision Research 40 (2000) 3507–3516 www.elsevier.com/locate/visres Perceived speed of motion in depth is reduced in the periphery K. Brooks *, G. Mather Experimental Psychology, Biology School, Uni6ersity of Sussex, Brighton BN19QG, UK Received 24 February 1999; received in revised form 30 November 1999 Abstract The perceived speed of motion in depth (MID) for a monocularly visible target was measured in central and peripheral vision using a 2AFC speed discrimination task. Only binocular cues to MID were available: changing disparity and interocular velocity difference (IOVD). Perceived speed for monocular lateral motion and perceived depth for static disparity were also assessed, again in both central and peripheral vision. The purpose of the experiment was to assess the relative contributions of changing disparity and IOVD cues to the perceived speed of stereomotion. Although peripheral stimuli appeared to lie at approximately the same depth as their central counterparts, their apparent speed was reduced. Monocular/lateral and binocular/MID speeds were reduced to a similar extent. It seems that reduced apparent monocular speed leads to reduced perceived MID speed, despite the fact that the disparity system appears to be unaffected. These results suggest that the IOVD cue makes a significant contribution to MID speed perception. © 2000 Published by Elsevier Science Ltd. Keywords: Motion in depth; Speed discrimination; Peripheral vision 1. Introduction motion in depth (MID) could be encoded by the mo- tion system, without the need for disparity sensitive Consider the motion of an object approaching an mechanisms. A unit capable of assessing the difference observer along the median plane. Three major cues to in velocity of each monocular motion signal could be the speed of the object are available.
    [Show full text]
  • Peripheral Viewing During Exposure to a 2D/3D Video Clip: Effects on the Human Body
    Environ Health Prev Med (2015) 20:79–89 DOI 10.1007/s12199-014-0424-4 REGULAR ARTICLE Peripheral viewing during exposure to a 2D/3D video clip: effects on the human body Masumi Takada • Yuta Fukui • Yasuyuki Matsuura • Motohiko Sato • Hiroki Takada Received: 30 October 2014 / Accepted: 10 November 2014 / Published online: 24 December 2014 Ó The Japanese Society for Hygiene 2014 Abstract changed remarkably after the 3D video clip was viewed Objectives Symptoms of three-dimensional (3D) sickness, peripherally and produced a persistent instability in equi- such as intoxication and eye fatigue, have been observed in librium function. The questionnaire findings also signifi- subjects viewing 3D films and vary according to the image cantly changed after the subjects viewed the video clips quality and visual environment. In addition, the influence of peripherally. stereoscopic vision on the incidence of 3D sickness has not Conclusions Subjective exacerbation and deterioration of been explored sufficiently. Therefore, it is important to equilibrium function were observed after peripheral view- examine the safety of viewing virtual 3D content. ing of 3D video clips. This persistent influence may result Methods The present study examines the effects of when subjects view a poorly depicted background element peripheral vision on reported motion sickness during expo- peripherally, which generates depth perception that con- sure to 2D/3D video clips for 1 min and for 1 min afterwards tradicts daily experience. in human subjects. Stabilograms were recorded during exposure to video clips with or without visual pursuit of a 3D Keywords Body sway Á Stabilogram Á Stereoscopic object and compared, and subjects were administered the image Á Simulator sickness questionnaire Á SSQ simulator sickness questionnaire after stabilometry.
    [Show full text]
  • Perceiving Self-Motion in Depth: the Role of Stereoscopic Motion and Changing-Size Cues
    Perception & Psychophysics 1996,58 (8), JJ68-JJ76 Perceiving self-motion in depth: The role of stereoscopic motion and changing-size cues STEPHEN PALMISANO University ofNew South Wales, Kensington, New South Wales, Australia During self-motions, different patterns of optic flow are presented to the left and right eyes. Previ­ ous research has, however, focused mainly on the self-motion information contained in a single pattern of optic flow. The present experiments investigated the role that binocular disparity plays in the visual perception of self-motion, showing that the addition of stereoscopic cues to optic flow significantly im­ proves forward linear vection in central vision. Improvements were also achieved by adding changing­ size cues to sparse (but not dense) flow patterns. These findings showedthat assumptions in the head­ ing literature that stereoscopic cues facilitate self-motion only when the optic flow has ambiguous depth ordering do not apply to vection. Rather, it was concluded that both stereoscopic and changing­ size cues provide additional motion-in-depth information that is used in perceiving self-motion. Ofall the senses known to be involved in self-motion During self-motions, different patterns of optic flow perception-the vestibular, auditory, somatosensory, pro­ are presented to the left and right eyes (due to the sepa­ prioceptive, and visual systems-visionappears to play the ration ofthe eyes and their different angles ofregard; see dominant role (Benson, 1990; Howard, 1982). This is Figure 1). Theorists have, however, generally focused only demonstrated by the fact that compelling illusions of on the motion-perspective information contained in a sin­ self-motion can be induced by visual information alone.
    [Show full text]
  • Peripheral Vision and Visual Attention Randall William Adams Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1971 Peripheral vision and visual attention Randall William Adams Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Experimental Analysis of Behavior Commons, and the Psychiatry and Psychology Commons Recommended Citation Adams, Randall William, "Peripheral vision and visual attention " (1971). Retrospective Theses and Dissertations. 4933. https://lib.dr.iastate.edu/rtd/4933 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. I I 72-5168 ADAMS, Randall William, 1941- PERIPHERAL VISION AND VISUAL ATTENTION. Iowa State University, Ph.D., 1971 Psychology, e^erimental University Microfilms, A XEROX Company, Ann Arbor, Michigan THIS DISSERTATION HAS BEEN MICROFILMED EXACTLY AS RECEIVED Peripheral vision and visual attention by Randall William Adams A Dissertation Submitted to the Graduate Faculty in Partial Fulfillment of The Requirements for the Degree of DOCTOR OF PHILOSOPHY Major Subject: Psychology Approved: Signature was redacted for privacy. In Charge of Major Work Signature was redacted for privacy. For the Major Department Signature was redacted for privacy. Foi^thé/Gifeduate College Iowa State University Mes, Iowa 1971 ii TABLE OF CONTENTS Page INTRODUCTION MD LITERATURE REVIEW 1 STUDY I 12 STUDY II 30 GENERAL DISCUSSION 39 LITERATURE CITED ' 4.5 ACKNOWLEDGEMENTS 47 APPENDIX A. VISUAL CHARACTERS AND TIME INTERVALS USED FOR PERIPHERAL TASK (STUDY I) 4.8 APPENDIX B.
    [Show full text]