Variable Selection Via Penalized Regression and the Genetic Algorithm Using Information Complexity, with Applications for High-Dimensional -Omics Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
European Patent Office of Opposition to That Patent, in Accordance with the Implementing Regulations
(19) TZZ Z_T (11) EP 2 884 280 B1 (12) EUROPEAN PATENT SPECIFICATION (45) Date of publication and mention (51) Int Cl.: of the grant of the patent: G01N 33/566 (2006.01) 09.05.2018 Bulletin 2018/19 (21) Application number: 13197310.9 (22) Date of filing: 15.12.2013 (54) Method for evaluating the scent performance of perfumes and perfume mixtures Verfahren zur Bewertung des Duftverhaltens von Duftstoffen und Duftstoffmischungen Procédé d’evaluation de senteur performance du parfums et mixtures de parfums (84) Designated Contracting States: (56) References cited: AL AT BE BG CH CY CZ DE DK EE ES FI FR GB WO-A2-03/091388 GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO PL PT RO RS SE SI SK SM TR • BAGHAEI KAVEH A: "Deorphanization of human olfactory receptors by luciferase and Ca-imaging (43) Date of publication of application: methods.",METHODS IN MOLECULAR BIOLOGY 17.06.2015 Bulletin 2015/25 (CLIFTON, N.J.) 2013, vol. 1003, 19 June 2013 (2013-06-19), pages229-238, XP008168583, ISSN: (73) Proprietor: Symrise AG 1940-6029 37603 Holzminden (DE) • KAVEH BAGHAEI ET AL: "Olfactory receptors coded by segregating pseudo genes and (72) Inventors: odorants with known specific anosmia.", 33RD • Hatt, Hanns ANNUAL MEETING OF THE ASSOCIATION FOR 44789 Bochum (DE) CHEMORECEPTION, 1 April 2011 (2011-04-01), • Gisselmann, Günter XP055111507, 58456 Witten (DE) • TOUHARA ET AL: "Deorphanizing vertebrate • Ashtibaghaei, Kaveh olfactory receptors: Recent advances in 44801 Bochum (DE) odorant-response assays", NEUROCHEMISTRY • Panten, Johannes INTERNATIONAL, PERGAMON PRESS, 37671 Höxter (DE) OXFORD, GB, vol. -

Qt4vh1p2c4 Nosplash E372185
Copyright 2014 by Janine Micheli-Jazdzewski ii Dedication I would like to dedicate this thesis to Rock, who is not with us anymore, TR, General Jack D. Ripper, and Page. Thank you for sitting with me while I worked for countless hours over the years. iii Acknowledgements I would like to express my special appreciation and thanks to my advisor Dr. Deanna Kroetz, you have been a superb mentor for me. I would like to thank you for encouraging my research and for helping me to grow as a research scientist. Your advice on both research, as well as on my career have been priceless. I would also like to thank my committee members, Dr. Laura Bull, Dr. Steve Hamilton and Dr. John Witte for guiding my research and expanding my knowledge on statistics, genetics and clinical phenotypes. I also want to thank past and present members of my laboratory for their support and help over the years, especially Dr. Mike Baldwin, Dr. Sveta Markova, Dr. Ying Mei Liu and Dr. Leslie Chinn. Thanks are also due to my many collaborators that made this research possible including: Dr. Eric Jorgenson, Dr. David Bangsberg, Dr. Taisei Mushiroda, Dr. Michiaki Kubo, Dr. Yusuke Nakamura, Dr. Jeffrey Martin, Joel Mefford, Dr. Sarah Shutgarts, Dr. Sulggi Lee and Dr. Sook Wah Yee. A special thank you to the RIKEN Center for Genomic Medicine that generously performed the genome-wide genotyping for these projects. Thanks to Dr. Steve Chamow, Dr. Bill Werner, Dr. Montse Carrasco, and Dr. Teresa Chen who started me on the path to becoming a scientist. -

Pathogenetic Subgroups of Multiple Myeloma Patients
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector ARTICLE High-resolution genomic profiles define distinct clinico- pathogenetic subgroups of multiple myeloma patients Daniel R. Carrasco,1,2,8 Giovanni Tonon,1,8 Yongsheng Huang,3,8 Yunyu Zhang,1 Raktim Sinha,1 Bin Feng,1 James P. Stewart,3 Fenghuang Zhan,3 Deepak Khatry,1 Marina Protopopova,5 Alexei Protopopov,5 Kumar Sukhdeo,1 Ichiro Hanamura,3 Owen Stephens,3 Bart Barlogie,3 Kenneth C. Anderson,1,4 Lynda Chin,1,7 John D. Shaughnessy, Jr.,3,9 Cameron Brennan,6,9 and Ronald A. DePinho1,5,9,* 1 Department of Medical Oncology, Dana-Farber Cancer Institute, Boston, Massachusetts 02115 2 Department of Pathology, Brigham and Women’s Hospital, Boston, Massachusetts 02115 3 The Donna and Donald Lambert Laboratory of Myeloma Genetics, Myeloma Institute for Research and Therapy, University of Arkansas for Medical Sciences, Little Rock, Arkansas 72205 4 The Jerome Lipper Multiple Myeloma Center, Department of Medical Oncology, Dana-Farber Cancer Institute, Boston, Massachusetts 02115 5 Center for Applied Cancer Science, Belfer Institute for Innovative Cancer Science, Dana-Farber Cancer Institute, Harvard Medical School, Boston, Massachusetts 6 Neurosurgery Service, Memorial Sloan-Kettering Cancer Center, Department of Neurosurgery, Weill Cornell Medical College, New York, New York 10021 7 Department of Dermatology, Brigham and Women’s Hospital and Harvard Medical School, Boston, Massachusetts, 02115 8 These authors contributed equally to this work. 9 Cocorresponding authors: [email protected] (C.B.); [email protected] (J.D.S.); [email protected] (R.A.D.) *Correspondence: [email protected] Summary To identify genetic events underlying the genesis and progression of multiple myeloma (MM), we conducted a high-resolu- tion analysis of recurrent copy number alterations (CNAs) and expression profiles in a collection of MM cell lines and out- come-annotated clinical specimens. -

WO 2019/068007 Al Figure 2
(12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization I International Bureau (10) International Publication Number (43) International Publication Date WO 2019/068007 Al 04 April 2019 (04.04.2019) W 1P O PCT (51) International Patent Classification: (72) Inventors; and C12N 15/10 (2006.01) C07K 16/28 (2006.01) (71) Applicants: GROSS, Gideon [EVIL]; IE-1-5 Address C12N 5/10 (2006.0 1) C12Q 1/6809 (20 18.0 1) M.P. Korazim, 1292200 Moshav Almagor (IL). GIBSON, C07K 14/705 (2006.01) A61P 35/00 (2006.01) Will [US/US]; c/o ImmPACT-Bio Ltd., 2 Ilian Ramon St., C07K 14/725 (2006.01) P.O. Box 4044, 7403635 Ness Ziona (TL). DAHARY, Dvir [EilL]; c/o ImmPACT-Bio Ltd., 2 Ilian Ramon St., P.O. (21) International Application Number: Box 4044, 7403635 Ness Ziona (IL). BEIMAN, Merav PCT/US2018/053583 [EilL]; c/o ImmPACT-Bio Ltd., 2 Ilian Ramon St., P.O. (22) International Filing Date: Box 4044, 7403635 Ness Ziona (E.). 28 September 2018 (28.09.2018) (74) Agent: MACDOUGALL, Christina, A. et al; Morgan, (25) Filing Language: English Lewis & Bockius LLP, One Market, Spear Tower, SanFran- cisco, CA 94105 (US). (26) Publication Language: English (81) Designated States (unless otherwise indicated, for every (30) Priority Data: kind of national protection available): AE, AG, AL, AM, 62/564,454 28 September 2017 (28.09.2017) US AO, AT, AU, AZ, BA, BB, BG, BH, BN, BR, BW, BY, BZ, 62/649,429 28 March 2018 (28.03.2018) US CA, CH, CL, CN, CO, CR, CU, CZ, DE, DJ, DK, DM, DO, (71) Applicant: IMMP ACT-BIO LTD. -
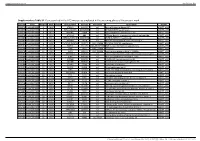
Supplementary Table S1. Genes Printed in the HC5 Microarray Employed in the Screening Phase of the Present Work
Supplementary material Ann Rheum Dis Supplementary Table S1. Genes printed in the HC5 microarray employed in the screening phase of the present work. CloneID Plate Position Well Length GeneSymbol GeneID Accession Description Vector 692672 HsxXG013989 2 B01 STK32A 202374 null serine/threonine kinase 32A pANT7_cGST 692675 HsxXG013989 3 C01 RPS10-NUDT3 100529239 null RPS10-NUDT3 readthrough pANT7_cGST 692678 HsxXG013989 4 D01 SPATA6L 55064 null spermatogenesis associated 6-like pANT7_cGST 692679 HsxXG013989 5 E01 ATP1A4 480 null ATPase, Na+/K+ transporting, alpha 4 polypeptide pANT7_cGST 692689 HsxXG013989 6 F01 ZNF816-ZNF321P 100529240 null ZNF816-ZNF321P readthrough pANT7_cGST 692691 HsxXG013989 7 G01 NKAIN1 79570 null Na+/K+ transporting ATPase interacting 1 pANT7_cGST 693155 HsxXG013989 8 H01 TNFSF12-TNFSF13 407977 NM_172089 TNFSF12-TNFSF13 readthrough pANT7_cGST 693161 HsxXG013989 9 A02 RAB12 201475 NM_001025300 RAB12, member RAS oncogene family pANT7_cGST 693169 HsxXG013989 10 B02 SYN1 6853 NM_133499 synapsin I pANT7_cGST 693176 HsxXG013989 11 C02 GJD3 125111 NM_152219 gap junction protein, delta 3, 31.9kDa pANT7_cGST 693181 HsxXG013989 12 D02 CHCHD10 400916 null coiled-coil-helix-coiled-coil-helix domain containing 10 pANT7_cGST 693184 HsxXG013989 13 E02 IDNK 414328 null idnK, gluconokinase homolog (E. coli) pANT7_cGST 693187 HsxXG013989 14 F02 LYPD6B 130576 null LY6/PLAUR domain containing 6B pANT7_cGST 693189 HsxXG013989 15 G02 C8orf86 389649 null chromosome 8 open reading frame 86 pANT7_cGST 693194 HsxXG013989 16 H02 CENPQ 55166 -

The Effect of Compound L19 on Human Colorectal Cells (DLD-1)
Stephen F. Austin State University SFA ScholarWorks Electronic Theses and Dissertations Spring 5-16-2018 The Effect of Compound L19 on Human Colorectal Cells (DLD-1) Sepideh Mohammadhosseinpour [email protected] Follow this and additional works at: https://scholarworks.sfasu.edu/etds Part of the Biotechnology Commons Tell us how this article helped you. Repository Citation Mohammadhosseinpour, Sepideh, "The Effect of Compound L19 on Human Colorectal Cells (DLD-1)" (2018). Electronic Theses and Dissertations. 188. https://scholarworks.sfasu.edu/etds/188 This Thesis is brought to you for free and open access by SFA ScholarWorks. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of SFA ScholarWorks. For more information, please contact [email protected]. The Effect of Compound L19 on Human Colorectal Cells (DLD-1) Creative Commons License This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. This thesis is available at SFA ScholarWorks: https://scholarworks.sfasu.edu/etds/188 The Effect of Compound L19 on Human Colorectal Cells (DLD-1) By Sepideh Mohammadhosseinpour, Master of Science Presented to the Faculty of the Graduate School of Stephen F. Austin State University In Partial Fulfillment Of the Requirements For the Degree of Master of Science in Biotechnology STEPHEN F. AUSTIN STATE UNIVERSITY May, 2018 The Effect of Compound L19 on Human Colorectal Cells (DLD-1) By Sepideh Mohammadhosseinpour, Master of Science APPROVED: Dr. Beatrice A. Clack, Thesis Director Dr. Josephine Taylor, Committee Member Dr. Rebecca Parr, Committee Member Dr. Stephen Mullin, Committee Member Pauline Sampson, Ph.D. -

Clinical, Molecular, and Immune Analysis of Dabrafenib-Trametinib
Supplementary Online Content Chen G, McQuade JL, Panka DJ, et al. Clinical, molecular and immune analysis of dabrafenib-trametinib combination treatment for metastatic melanoma that progressed during BRAF inhibitor monotherapy: a phase 2 clinical trial. JAMA Oncology. Published online April 28, 2016. doi:10.1001/jamaoncol.2016.0509. eMethods. eReferences. eTable 1. Clinical efficacy eTable 2. Adverse events eTable 3. Correlation of baseline patient characteristics with treatment outcomes eTable 4. Patient responses and baseline IHC results eFigure 1. Kaplan-Meier analysis of overall survival eFigure 2. Correlation between IHC and RNAseq results eFigure 3. pPRAS40 expression and PFS eFigure 4. Baseline and treatment-induced changes in immune infiltrates eFigure 5. PD-L1 expression eTable 5. Nonsynonymous mutations detected by WES in baseline tumors This supplementary material has been provided by the authors to give readers additional information about their work. © 2016 American Medical Association. All rights reserved. Downloaded From: https://jamanetwork.com/ on 09/30/2021 eMethods Whole exome sequencing Whole exome capture libraries for both tumor and normal samples were constructed using 100ng genomic DNA input and following the protocol as described by Fisher et al.,3 with the following adapter modification: Illumina paired end adapters were replaced with palindromic forked adapters with unique 8 base index sequences embedded within the adapter. In-solution hybrid selection was performed using the Illumina Rapid Capture Exome enrichment kit with 38Mb target territory (29Mb baited). The targeted region includes 98.3% of the intervals in the Refseq exome database. Dual-indexed libraries were pooled into groups of up to 96 samples prior to hybridization. -

Analysis of Tissue-Specific & Allele- Specific DNA Methylation
Analysis of tissue-specific & allele- specific DNA methylation Dissertation zur Erlangung des Doktorgrades der Naturwissenschaften (Dr. rer. nat.) der Naturwissenschaftlichen Fakultät IV – Chemie und Pharmazie der Universität Regensburg vorgelegt von Elmar Schilling aus Schwenningen 2009 The present work was carried out in the Department of Hematology and Oncology at the University Hospital Regensburg from June 2005 to June 2009 and was supervised by PD. Dr. Michael Rehli. Die vorliegende Arbeit entstand in der Zeit von Juni 2005 bis Juni 2009 in der Abteilung für Hämatologie und internistische Onkologie des Klinikums der Universität Regensburg unter der Anleitung von PD. Dr. Michael Rehli. Promotionsgesuch eingereicht am: 30. Juli 2009 Die Arbeit wurde angeleitet von PD. Dr. Michael Rehli. Prüfungsausschuss: Vorsitzender: Prof. Dr. Sigurd Elz 1. Gutachter: Prof. Dr. Roland Seifert 2. Gutachter: PD. Dr. Michael Rehli 3. Prüfer: Prof. Dr. Gernot Längst Lob und Tadel bringen den Weisen nicht aus dem Gleichgewicht. (Budha) TABLE OF CONTENTS 1 INTRODUCTION .............................................................................................. 1 1.1 THE CONCEPT OF EPIGENETICS ............................................................................................. 1 1.2 DNA METHYLATION .............................................................................................................. 2 1.2.1 DNA methyltransferases ................................................................................................ 3 1.2.2 -

Olfactory Receptor 6Q1 Rabbit Pab Antibody
Olfactory receptor 6Q1 rabbit pAb antibody Catalog No : Source: Concentration : Mol.Wt. (Da): A18981 Rabbit 1 mg/ml 35618 Applications WB,IF,ELISA Reactivity Human Dilution WB: 1:500 - 1:2000. IF: 1:200 - 1:1000. ELISA: 1:20000. Not yet tested in other applications. Storage -20°C/1 year Specificity Olfactory receptor 6Q1 Polyclonal Antibody detects endogenous levels of Olfactory receptor 6Q1 protein. Source / Purification The antibody was affinity-purified from rabbit antiserum by affinity- chromatography using epitope-specific immunogen. Immunogen The antiserum was produced against synthesized peptide derived from human OR6Q1. AA range:23-72 Uniprot No Q8NGQ2 Alternative names OR6Q1; Olfactory receptor 6Q1; Olfactory receptor OR11-226 Form Liquid in PBS containing 50% glycerol, 0.5% BSA and 0.02% sodium azide. Clonality Polyclonal Isotype IgG Conjugation Background olfactory receptor family 6 subfamily Q member 1 (gene/pseudogene) (OR6Q1) Homo sapiens Olfactory receptors interact with odorant molecules in the nose, to initiate a neuronal response that triggers the perception of a smell. The olfactory receptor proteins are members of a large family of G-protein-coupled receptors (GPCR) arising from single coding- exon genes. Olfactory receptors share a 7-transmembrane domain structure with many neurotransmitter and hormone receptors and are responsible for the recognition and G protein-mediated transduction of odorant signals. The olfactory receptor gene family is the largest in the genome. The nomenclature assigned to the olfactory receptor genes and proteins for this organism is independent of other organisms. This olfactory receptor gene is a segregating pseudogene, where some individuals have an allele that encodes a functional olfactory receptor, while other individuals have an allele encoding a Other OR6Q1, Olfactory receptor 6Q1 A AAB Biosciences Products www.aabsci.cn FOR RESEARCH USE ONLY. -

AKT-Mtor Signaling in Human Acute Myeloid Leukemia Cells and Its Association with Adverse Prognosis
Cancers 2018, 10, 332 S1 of S35 Supplementary Materials: Clonal Heterogeneity Reflected by PI3K- AKT-mTOR Signaling in Human Acute Myeloid Leukemia Cells and its Association with Adverse Prognosis Ina Nepstad, Kimberley Joanne Hatfield, Tor Henrik Anderson Tvedt, Håkon Reikvam and Øystein Bruserud Figure S1. Detection of clonal heterogeneity for 49 acute myeloid leukemia (AML) patients; the results from representative flow cytometric analyses of phosphatidylinositol-3-kinase-Akt-mechanistic target of rapamycin (PI3K-Akt-mTOR) activation. For each patient clonal heterogeneity was detected by analysis Cancers 2018, 10, 332 S2 of S35 of at least one mediator in the PI3K-Akt-mTOR pathway. Patient ID is shown in the upper right corner of each histogram. The figure documents the detection of dual populations for all patients, showing the results from one representative flow cytometric analysis for each of these 49 patients. The Y-axis represents the amount of cells, and the X-axis represents the fluorescence intensity. The stippled line shows the negative/unstained controls. Figure S2. Cell preparation and gating strategy. Flow cytometry was used for examination of the constitutive expression of the mediators in the PI3K-Akt-mTOR pathway/network in primary AML cells. Cryopreserved cells were thawed and washed before suspension cultures were prepared as described in Materials and methods. Briefly, cryopreserved and thawed primary leukemic cells were incubated for 20 minutes in RPMI-1640 (Sigma-Aldrich) before being directly fixed in 1.5% paraformaldehyde (PFA) and permeabilized with 100% ice-cold methanol. The cells were thereafter rehydrated by adding 2 mL phosphate buffered saline (PBS), gently re-suspended and then centrifuged. -

The Hypothalamus As a Hub for SARS-Cov-2 Brain Infection and Pathogenesis
bioRxiv preprint doi: https://doi.org/10.1101/2020.06.08.139329; this version posted June 19, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. The hypothalamus as a hub for SARS-CoV-2 brain infection and pathogenesis Sreekala Nampoothiri1,2#, Florent Sauve1,2#, Gaëtan Ternier1,2ƒ, Daniela Fernandois1,2 ƒ, Caio Coelho1,2, Monica ImBernon1,2, Eleonora Deligia1,2, Romain PerBet1, Vincent Florent1,2,3, Marc Baroncini1,2, Florence Pasquier1,4, François Trottein5, Claude-Alain Maurage1,2, Virginie Mattot1,2‡, Paolo GiacoBini1,2‡, S. Rasika1,2‡*, Vincent Prevot1,2‡* 1 Univ. Lille, Inserm, CHU Lille, Lille Neuroscience & Cognition, DistAlz, UMR-S 1172, Lille, France 2 LaBoratorY of Development and PlasticitY of the Neuroendocrine Brain, FHU 1000 daYs for health, EGID, School of Medicine, Lille, France 3 Nutrition, Arras General Hospital, Arras, France 4 Centre mémoire ressources et recherche, CHU Lille, LiCEND, Lille, France 5 Univ. Lille, CNRS, INSERM, CHU Lille, Institut Pasteur de Lille, U1019 - UMR 8204 - CIIL - Center for Infection and ImmunitY of Lille (CIIL), Lille, France. # and ƒ These authors contriButed equallY to this work. ‡ These authors directed this work *Correspondence to: [email protected] and [email protected] Short title: Covid-19: the hypothalamic hypothesis 1 bioRxiv preprint doi: https://doi.org/10.1101/2020.06.08.139329; this version posted June 19, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. -

Supplemental Table 1 (S1). the Chromosomal Regions and Genes Exhibiting Loss of Heterozygosity That Were Shared Between the HLRCC-Rccs of Both Patients 1 and 2
BMJ Publishing Group Limited (BMJ) disclaims all liability and responsibility arising from any reliance Supplemental material placed on this supplemental material which has been supplied by the author(s) J Clin Pathol Supplemental Table 1 (S1). The chromosomal regions and genes exhibiting loss of heterozygosity that were shared between the HLRCC-RCCs of both Patients 1 and 2. Chromosome Position Genes 1 p13.1 ATP1A1, ATP1A1-AS1, LOC101929023, CD58, IGSF3, MIR320B1, C1orf137, CD2, PTGFRN, CD101, LOC101929099 1 p21.1* COL11A1, LOC101928436, RNPC3, AMY2B, ACTG1P4, AMY2A, AMY1A, AMY1C, AMY1B 1 p36.11 LOC101928728, ARID1A, PIGV, ZDHHC18, SFN, GPN2, GPATCH3, NR0B2, NUDC, KDF1, TRNP1, FAM46B, SLC9A1, WDTC1, TMEM222, ACTG1P20, SYTL1, MAP3K6, FCN3, CD164L2, GPR3, WASF2, AHDC1, FGR, IFI6 1 q21.3* KCNN3, PMVK, PBXIP1, PYGO2, LOC101928120, SHC1, CKS1B, MIR4258, FLAD1, LENEP, ZBTB7B, DCST2, DCST1, LOC100505666, ADAM15, EFNA4, EFNA3, EFNA1, SLC50A1, DPM3, KRTCAP2, TRIM46, MUC1, MIR92B, THBS3, MTX1, GBAP1, GBA, FAM189B, SCAMP3, CLK2, HCN3, PKLR, FDPS, RUSC1-AS1, RUSC1, ASH1L, MIR555, POU5F1P4, ASH1L-AS1, MSTO1, MSTO2P, YY1AP1, SCARNA26A, DAP3, GON4L, SCARNA26B, SYT11, RIT1, KIAA0907, SNORA80E, SCARNA4, RXFP4, ARHGEF2, MIR6738, SSR2, UBQLN4, LAMTOR2, RAB25, MEX3A, LMNA, SEMA4A, SLC25A44, PMF1, PMF1-BGLAP 1 q24.2–44* LOC101928650, GORAB, PRRX1, MROH9, FMO3, MIR1295A, MIR1295B, FMO6P, FMO2, FMO1, FMO4, TOP1P1, PRRC2C, MYOC, VAMP4, METTL13, DNM3, DNM3-IT1, DNM3OS, MIR214, MIR3120, MIR199A2, C1orf105, PIGC, SUCO, FASLG, TNFSF18, TNFSF4, LOC100506023, LOC101928673,