DOCSLIB.ORG

A Highly Symmetric Two-Handed Metamaterial Spontaneously Matching the Wave Impedance

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Highly Symmetric Two-Handed Metamaterial Spontaneously Matching the Wave Impedance A highly symmetric two-handed metamaterial spontaneously matching the wave impedance Yi- Ju Chiang1 and Ta-Jen Yen1,2† 1 Department of Materials Science and Engineering, National Tsing Hua University, Hsinchu 30013, Taiwan, R.O.C. 2 Institute of NanoEngineering and MicroSystems, National Tsing Hua University, 101, Section 2, Kuang Fu Road, Hsinchu 30013, Taiwan, R.O.C. † E-mail: [email protected]; Tel: 886-3-5742174; Fax: 886-3-5722366 Abstract: We demonstrate a two-handed metamaterial (THM), composed of highly symmetric three-layered structures operated at normal incidence. Not only does the THM exhibit two distinct allowed bands with right- handed and left-handed electromagnetic responses, but posses a further advantage of being independent to the polarizations of external excitations. In addition, the THM automatically matches the wave impedance in free space, leading to maximum transmittances about 0.8 dB in the left-handed band and almost 0 dB in the right-handed band, respectively. Such a THM can be employed for diverse electromagnetic devices including dual-band bandpass filters, ultra-wide bandpass filters and superlenses. ©2008 Optical Society of America OCIS codes: (160.3918) Metamaterials; (350.3618) Left-handed materials; (260.5740) Resonance; (350.4010) Microwaves. References and links 1. J. D. Watson, and F. H. C. Crick, "Molecular Structure of Nucleic Acids," Nature 171, 737-738 (1953). 2. A. H. J. Wang, G. J. Quigley, F. J. Kolpak, J. L. Crawford, J. H. Vanboom, G. Van der Marel, and A. Rich, "Molecular structure of a left-handed double helical DNA fragment at atomic resolution," Nature 282, 680- 686 (1979). 3. V. G. Veselago, "The electrodynamics of substances with simultaneously negative values of permittivity and permeability," Sov. Phys. Usp. 10, 509 (1968). 4. J. B. Pendry, A. J. Holden, W. J. Stewart, and I. Youngs, "Extremely low frequency plasmons in metallic mesostructures," Phys. Rev. Lett. 76, 4773-4776 (1996). 5. J. B. Pendry, A. J. Holden, D. J. Robbins, and W. J. Stewart, "Magnetism from conductors and enhanced nonlinear phenomena," IEEE Trans. Microwave Theory Tech. 47, 2075-2084 (1999). 6. D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser, and S. Schultz, "Composite medium with simultaneously negative permeability and permittivity," Phys. Rev. Lett. 84, 4184-4187 (2000). 7. R. A. Shelby, D. R. Smith, and S. Schultz, "Experimental verification of a negative index of refraction," Science 292, 77-79 (2001). 8. A. A. Houck, J. B. Brock, and I. L. Chuang, "Experimental observations of a left-handed material that obeys Snell's law," Phys. Rev. Lett. 90, 137401 (2003). 9. N. Seddon, and T. Bearpark, "Observation of the inverse Doppler effect," Science 302, 1537-1540 (2003). 10. J. Lu, T. M. Grzegorczyk, Y. Zhang, J. Pacheco, B. I. Wu, J. A. Kong, and M. Chen, "Cerenkov radiation in materials with negative permittivity and permeability," Opt. Express 11, 723-734 (2003). 11. J. B. Pendry, "Negative refraction makes a perfect lens," Phys. Rev. Lett. 85, 3966-3969 (2000). 12. N. Fang, H. Lee, C. Sun, and X. Zhang, "Sub-diffraction-limited optical imaging with a silver superlens," Science 308, 534-537 (2005). 13. V. M. Shalaev, W. S. Cai, U. K. Chettiar, H. K. Yuan, A. K. Sarychev, V. P. Drachev, and A. V. Kildishev, "Negative index of refraction in optical metamaterials," Opt. Lett. 30, 3356-3358 (2005). 14. G. V. Eleftheriades, A. K. Iyer, and P. C. Kremer, "Planar negative refractive index media using periodically L-C loaded transmission lines," IEEE Trans. Microwave Theory Tech. 50, 2702-2712 (2002). 15. J. F. Zhou, T. Koschny, L. Zhang, G. Tuttle, and C. M. Soukoulis, "Experimental demonstration of negative index of refraction," Appl. Phys. Lett. 88, 221103 (2006). 16. I. Gil, J. Bonache, M. Gil, J. Garcia-Garcia, and F. Martin, "Left-handed and right-handed transmission properties of microstrip lines loaded with complementary split rings resonators," Microwave Opt. Tech. Lett. 48, 2508-2511 (2006). 17. L. Ran, J. Huangfu, H. Chen, Y. Li, X. Zhang, K. Chen, and J. A. Kong, "Microwave solid-state left-handed material with a broad bandwidth and an ultralow loss," Physical Review B 70 (2004). #97050 - $15.00 USD Received 5 Jun 2008; revised 17 Jul 2008; accepted 19 Jul 2008; published 7 Aug 2008 (C) 2008 OSA 18 August 2008 / Vol. 16, No. 17 / OPTICS EXPRESS 12764 18. J. F. Zhou, L. Zhang, G. Tuttle, T. Koschny, and C. M. Soukoulis, "Negative index materials using simple short wire pairs," Phys. Rev. B 73, 041101 (2006). 19. H. S. Chen, L. X. Ran, J. T. Huangfu, X. M. Zhang, and K. S. Chen, "Left-handed materials composed of only S-shaped resonators," Phys. Rev. E 70, 057605 (2004). 20. D. R. Smith, S. Schultz, P. Markos, and C. M. Soukoulis, "Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients," Phys. Rev. B 65, 195104 (2002). 21. D. R. Smith, D. C. Vier, T. Koschny, and C. M. Soukoulis, "Electromagnetic parameter retrieval from inhomogeneous metamaterials," Phys. Rev. E 71, 036617 (2005). 22. T. Koschny, P. Markos, E. N. Economou, D. R. Smith, D. C. Vier, and C. M. Soukoulis, "Impact of inherent periodic structure on effective medium description of left-handed and related metamaterials," Phys. Rev. B 71, 245105 (2005). 23. T. Koschny, M. Kafesaki, E. N. Economou, and C. M. Soukoulis, "Effective medium theory of left-handed materials," Phys. Rev. Lett. 93, 107402 (2004). 24. N. Katsarakis, T. Koschny, M. Kafesaki, E. N. Economou, E. Ozbay, and C. M. Soukoulis, "Left- and right- handed transmission peaks near the magnetic resonance frequency in composite metamaterials," Phys. Rev. B 70, 201101 (2004). 25. K. Aydin, K. Guven, M. Kafesaki, L. Zhang, C. M. Soukoulis, and E. Ozbay, "Experimental observation of true left-handed transmission peaks in metamaterials," Opt. Lett. 29, 2623-2625 (2004). 26. B. A. Munk, Frequency Selective Surface: Theory and Design (John Wiley & Sons, Inc, 2000). 27. F. T. Ulaby, Fundamental of Applied Electromagnetics (Prentice-Hall, Inc., New Jersey, 1999). 28. N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith, and W. J. Padilla, "Perfect metamaterial absorber," Phys. Rev. Lett. 100, 207402 (2008). 1. Introduction It is an interesting observation that the right-handed systems appear to prevail in nature− for example, the major population of right-handed people, the right-handed helix of deoxyribonucleic acids (DNA) traced by the sugar-phosphate backbone [1] and certainly, electromagnetic (EM) responses of materials in which electric field E, magnetic field H, and wave vector k form a right-handed triplet of vectors. Although rare, the left-handed systems do exist in nature such as left-handed people and left-handed helical DNAs [2], the left- handed EM response in naturally occurring materials remains missing. Recently, a new class of artificially constructed sub-wavelength structures termed as metamaterials [3], possesses unprecedented EM properties to revise new chapters in electromagnetics. One revolutionary example is a negative-refractive-index medium [4-7], whose electric permittivity and magnetic permeability are negative simultaneously so that the relationship among E, H and k turns to be left-handed, leading to striking EM behaviors like inverse Snell’s law [7, 8], inverse Doppler shift [9], inverse Cerenkov effect [10], and superlensing effect [11, 12]. More interestingly, naturally occurring systems in fact allow the co-existence of both right-handed and left-handed sets (e.g., clearly observed in human beings and DNAs). As a consequence, to further enrich the possible EM properties of materials, in this letter we present a highly symmetric two-handed metamaterial (THM) to exhibit two distinct sets of EM responses. The designed THM and its corresponding geometric parameters are detailed in Fig. 1, presenting a four-fold symmetric periodic array composed of two metal discs sandwiching a dielectric layer to eventually form a continuous structure connected by very narrow metal “necks” with one another. In accordance with the dynamic Maxwell’s equations, as applying external excitations normal to the THM (i.e., along z-axis), the time-varying magnetic flux oscillating along the y- axis introduces antiparallel surface currents vertically (along the x-axis) within the two metal plates against the changing magnetic flux [13] and then results in artificial magnetic dipole moments oscillating along the y-axis. Established from the induced antiparallel surface currents, an L-C resonance occurs where the capacitance comes from the opposite charges in these two insulated metal plates and the inductance comes from the entire metals themselves, giving rise to a negative effective permeability (μeff) when such a magnetic response turns to be out-of-phase at frequencies just above the resonant frequency. Meanwhile, the metal stripes #97050 - $15.00 USD Received 5 Jun 2008; revised 17 Jul 2008; accepted 19 Jul 2008; published 7 Aug 2008 (C) 2008 OSA 18 August 2008 / Vol. 16, No. 17 / OPTICS EXPRESS 12765 Fig. 1. The fabricated THM (right panel) and the perspective view of a unit cell (left panel). The THM shows a four-fold symmetric sandwiched structure, composed of 17-m-thick copper plates and a Rogers TMM4 board with the relative dielectric constant of 4.5. The geometric parameters of the THM are as following: ax=ay=9.8 mm, r=4.75 mm, d= 0.7874 mm, h=0.30 mm, and w=0.28 mm. along E-field also contribute an additional shunt inductance, providing a negative effective permittivity (εeff) in the THM [14]. As a result, the THM exhibits both negative μeff and εeff at the same time to introduce the left-handed response (e.g., negative refraction) [3, 6]. On the other hand, once this sandwiched structure is at its off-resonance frequency, it exhibits a positive refractive index to behave the conventional right-handed response.
Load more

Recommended publications
  • Ec6503 - Transmission Lines and Waveguides Transmission Lines and Waveguides Unit I - Transmission Line Theory 1
    EC6503 - TRANSMISSION LINES AND WAVEGUIDES TRANSMISSION LINES AND WAVEGUIDES UNIT I - TRANSMISSION LINE THEORY 1. Define – Characteristic Impedance [M/J–2006, N/D–2006] Characteristic impedance is defined as the impedance of a transmission line measured at the sending end. It is given by 푍 푍0 = √ ⁄푌 where Z = R + jωL is the series impedance Y = G + jωC is the shunt admittance 2. State the line parameters of a transmission line. The line parameters of a transmission line are resistance, inductance, capacitance and conductance. Resistance (R) is defined as the loop resistance per unit length of the transmission line. Its unit is ohms/km. Inductance (L) is defined as the loop inductance per unit length of the transmission line. Its unit is Henries/km. Capacitance (C) is defined as the shunt capacitance per unit length between the two transmission lines. Its unit is Farad/km. Conductance (G) is defined as the shunt conductance per unit length between the two transmission lines. Its unit is mhos/km. 3. What are the secondary constants of a line? The secondary constants of a line are 푍 i. Characteristic impedance, 푍0 = √ ⁄푌 ii. Propagation constant, γ = α + jβ 4. Why the line parameters are called distributed elements? The line parameters R, L, C and G are distributed over the entire length of the transmission line. Hence they are called distributed parameters. They are also called primary constants. The infinite line, wavelength, velocity, propagation & Distortion line, the telephone cable 5. What is an infinite line? [M/J–2012, A/M–2004] An infinite line is a line where length is infinite.
    [Show full text]
  • Waveguides Waveguides, Like Transmission Lines, Are Structures Used to Guide Electromagnetic Waves from Point to Point. However
    Waveguides Waveguides, like transmission lines, are structures used to guide electromagnetic waves from point to point. However, the fundamental characteristics of waveguide and transmission line waves (modes) are quite different. The differences in these modes result from the basic differences in geometry for a transmission line and a waveguide. Waveguides can be generally classified as either metal waveguides or dielectric waveguides. Metal waveguides normally take the form of an enclosed conducting metal pipe. The waves propagating inside the metal waveguide may be characterized by reflections from the conducting walls. The dielectric waveguide consists of dielectrics only and employs reflections from dielectric interfaces to propagate the electromagnetic wave along the waveguide. Metal Waveguides Dielectric Waveguides Comparison of Waveguide and Transmission Line Characteristics Transmission line Waveguide • Two or more conductors CMetal waveguides are typically separated by some insulating one enclosed conductor filled medium (two-wire, coaxial, with an insulating medium microstrip, etc.). (rectangular, circular) while a dielectric waveguide consists of multiple dielectrics. • Normal operating mode is the COperating modes are TE or TM TEM or quasi-TEM mode (can modes (cannot support a TEM support TE and TM modes but mode). these modes are typically undesirable). • No cutoff frequency for the TEM CMust operate the waveguide at a mode. Transmission lines can frequency above the respective transmit signals from DC up to TE or TM mode cutoff frequency high frequency. for that mode to propagate. • Significant signal attenuation at CLower signal attenuation at high high frequencies due to frequencies than transmission conductor and dielectric losses. lines. • Small cross-section transmission CMetal waveguides can transmit lines (like coaxial cables) can high power levels.
    [Show full text]
  • Wave Guides Summary and Problems
    ECE 144 Electromagnetic Fields and Waves Bob York General Waveguide Theory Basic Equations (ωt γz) Consider wave propagation along the z-axis, with fields varying in time and distance according to e − . The propagation constant γ gives us much information about the character of the waves. We will assume that the fields propagating in a waveguide along the z-axis have no other variation with z,thatis,the transverse fields do not change shape (other than in magnitude and phase) as the wave propagates. Maxwell’s curl equations in a source-free region (ρ =0andJ = 0) can be combined to give the wave equations, or in terms of phasors, the Helmholtz equations: 2E + k2E =0 2H + k2H =0 ∇ ∇ where k = ω√µ. In rectangular or cylindrical coordinates, the vector Laplacian can be broken into two parts ∂2E 2E = 2E + ∇ ∇t ∂z2 γz so that with the assumed e− dependence we get the wave equations 2E +(γ2 + k2)E =0 2H +(γ2 + k2)H =0 ∇t ∇t (ωt γz) Substituting the e − into Maxwell’s curl equations separately gives (for rectangular coordinates) E = ωµH H = ωE ∇ × − ∇ × ∂Ez ∂Hz + γEy = ωµHx + γHy = ωEx ∂y − ∂y ∂Ez ∂Hz γEx = ωµHy γHx = ωEy − − ∂x − − − ∂x ∂Ey ∂Ex ∂Hy ∂Hx = ωµHz = ωEz ∂x − ∂y − ∂x − ∂y These can be rearranged to express all of the transverse fieldcomponentsintermsofEz and Hz,giving 1 ∂Ez ∂Hz 1 ∂Ez ∂Hz Ex = γ + ωµ Hx = ω γ −γ2 + k2 ∂x ∂y γ2 + k2 ∂y − ∂x w W w W 1 ∂Ez ∂Hz 1 ∂Ez ∂Hz Ey = γ + ωµ Hy = ω + γ γ2 + k2 − ∂y ∂x −γ2 + k2 ∂x ∂y w W w W For propagating waves, γ = β,whereβ is a real number provided there is no loss.
    [Show full text]
  • Uniform Plane Waves
    38 2. Uniform Plane Waves Because also ∂zEz = 0, it follows that Ez must be a constant, independent of z, t. Excluding static solutions, we may take this constant to be zero. Similarly, we have 2 = Hz 0. Thus, the fields have components only along the x, y directions: E(z, t) = xˆ Ex(z, t)+yˆ Ey(z, t) Uniform Plane Waves (transverse fields) (2.1.2) H(z, t) = xˆ Hx(z, t)+yˆ Hy(z, t) These fields must satisfy Faraday’s and Amp`ere’s laws in Eqs. (2.1.1). We rewrite these equations in a more convenient form by replacing and μ by: 1 η 1 μ = ,μ= , where c = √ ,η= (2.1.3) ηc c μ Thus, c, η are the speed of light and characteristic impedance of the propagation medium. Then, the first two of Eqs. (2.1.1) may be written in the equivalent forms: ∂E 1 ∂H ˆz × =− η 2.1 Uniform Plane Waves in Lossless Media ∂z c ∂t (2.1.4) ∂H 1 ∂E The simplest electromagnetic waves are uniform plane waves propagating along some η ˆz × = ∂z c ∂t fixed direction, say the z-direction, in a lossless medium {, μ}. The assumption of uniformity means that the fields have no dependence on the The first may be solved for ∂zE by crossing it with ˆz. Using the BAC-CAB rule, and transverse coordinates x, y and are functions only of z, t. Thus, we look for solutions noting that E has no z-component, we have: of Maxwell’s equations of the form: E(x, y, z, t)= E(z, t) and H(x, y, z, t)= H(z, t).
    [Show full text]
  • Microstrip Solutions for Innovative Microwave Feed Systems
    Examensarbete LiTH-ITN-ED-EX--2001/05--SE Microstrip Solutions for Innovative Microwave Feed Systems Magnus Petersson 2001-10-24 Department of Science and Technology Institutionen för teknik och naturvetenskap Linköping University Linköpings Universitet SE-601 74 Norrköping, Sweden 601 74 Norrköping LiTH-ITN-ED-EX--2001/05--SE Microstrip Solutions for Innovative Microwave Feed Systems Examensarbete utfört i Mikrovågsteknik / RF-elektronik vid Tekniska Högskolan i Linköping, Campus Norrköping Magnus Petersson Handledare: Ulf Nordh Per Törngren Examinator: Håkan Träff Norrköping den 24 oktober, 2001 'DWXP $YGHOQLQJ,QVWLWXWLRQ Date Division, Department Institutionen för teknik och naturvetenskap 2001-10-24 Ã Department of Science and Technology 6SUnN 5DSSRUWW\S ,6%1 Language Report category BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB Svenska/Swedish Licentiatavhandling X Engelska/English X Examensarbete ISRN LiTH-ITN-ED-EX--2001/05--SE C-uppsats 6HULHWLWHOÃRFKÃVHULHQXPPHUÃÃÃÃÃÃÃÃÃÃÃÃ,661 D-uppsats Title of series, numbering ___________________________________ _ ________________ Övrig rapport _ ________________ 85/I|UHOHNWURQLVNYHUVLRQ www.ep.liu.se/exjobb/itn/2001/ed/005/ 7LWHO Microstrip Solutions for Innovative Microwave Feed Systems Title )|UIDWWDUH Magnus Petersson Author 6DPPDQIDWWQLQJ Abstract This report is introduced with a presentation of fundamental electromagnetic theories, which have helped a lot in the achievement of methods for calculation and design of microstrip transmission lines and circulators. The used software for the work is also based on these theories. General considerations when designing microstrip solutions, such as different types of transmission lines and circulators, are then presented. Especially the design steps for microstrip lines, which have been used in this project, are described. Discontinuities, like bends of microstrip lines, are treated and simulated.
    [Show full text]
  • EMC Fundamentals
    ITU Training on Conformance and Interoperability for ARB Region CERT, 2-6 April 2013, EMC fundamentals Presented by: Karim Loukil & Kaïs Siala [email protected] [email protected] 1 Basics of electromagnetics 2 Electromagnetic waves A wave is a moving vibration λ Antenna V λ (m) = c(m/s) / F(Hz) 3 Definitions • The wavelength is the distance traveled by a wave in an oscillation cycle • Frequency is measured by the number of cycles per second and the unit is Hz . One cycle per second is one Hertz. 4 Electromagnetic waves (2) • An electromagnetic wave consists of: an electric field E (produced by the force of electric charges) a magnetic field H (produced by the movement of electric charges) • The fields E and H are orthogonal and are m oving at the speed of light 8 c = 3. 10 m/s 5 Electromagnetic waves (3) 6 E and H fields Electric field The field amplitude is l expressed in (V/m). E(V/m) Magnetic field The field amplitude is expressed in (A/m). d H(A /m) Power density Radiated power is perpendicular to a surface, divided by the area of ​​the surface. The power density is expressed as S (W / m²), or (mW /cm ²) , or (µW / cm ²). 7 E and H fields • Near a whip, the dominant field is the E field. The impedance in this area is Zc > 377 ohms. • Near a loop, the dominant field is the H field. The impedance in this area is Z c <377 ohms. 8 Plane wave 9 The EMC way of thinking Electrical domain Electromagnetic domain Voltage V (Volt) Electric Field E (V/m) Current I (Amp) Magnetic field H (A/m) Impedance Z (Ohm) Characteristic
    [Show full text]
  • Substrate Integrated Waveguide (SIW) Is a Very Promising Technique in That We Can Make Use of the Advantages of Both Waveguides and Planar Transmission Lines
    UNIVERSITÉ DE MONTRÉAL TUNABLE FERRITE PHASE SHIFTERS USING SUBSTRATE INTEGRATED WAVEGUIDE TECHNIQUE YONG JU BAN DÉPARTEMENT DE GÉNIE ÉLECTRIQUE ÉCOLE POLYTECHNIQUE DE MONTRÉAL MÉMOIRE PRÉSENTÉ EN VUE DE L‟OBTENTION DU DIPLÔ ME DE MAÎTRISE ÈS SCIENCES APPLIQUÉES (GÉNIE ÉLECTRIQUE) DÉCEMBRE 2010 © Yong Ju Ban, 2010. UNIVERSITÉ DE MONTRÉAL ÉCOLE POLYTECHNIQUE DE MONTRÉAL Ce mémoire intitulé: TUNABLE FERRITE PHASE SHIFTERS USING SUBSTRATE INTEGRATED WAVEGUIDE TECHNIQUE présenté par : BAN, YONG JU en vue de l‟obtention du diplôme de : Maîtrise ès sciences appliquées a été dûment accepté par le jury d‟examen constitué de : M. CARDINAL, Christian, Ph. D., président M. WU, Ke, Ph. D., membre et directeur de recherche M. DESLANDES, Dominic, Ph. D., membre iii DEDICATION To my lovely wife Jeong Min And my two sons Jione & Junone iv ACKNOWLEDGEMENTS I would like to express my sincere gratitude to my supervisor, Prof. Ke Wu, for having accepted me and given me the opportunity to pursue my master study in such a challenging and exciting research field, and for his invaluable guidance and encouragement throughout the work involved in this thesis. I would like to thank Mr. Jules Gauthier, Mr. Jean-Sebastien Décarie and other staffs of Poly-Grames Research Center for their skillful technical supports during my study and experiments. I thank Zhenyu Zhang, Fanfan He and Anthony Ghiotto for their helpful discussions. And many thanks should be extended to Sulav Adhikari for his invaluable supports for my study and thesis. I also appreciate my colleagues Xiaoma Jiang, Nikolay Volobouev, Adrey Taikov, Marie Chantal, Parmeet Chawala, Jawad Abdulnour and Shyam Gupta in SDP for their understanding and endurance for my study.
    [Show full text]
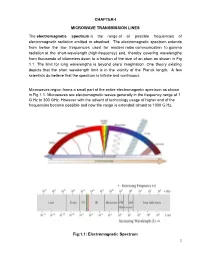
  • CHAPTER-I MICROWAVE TRANSMISSION LINES the Electromagnetic Spectrum Is the Range of All Possible Frequencies of Electromagnetic
    CHAPTER-I MICROWAVE TRANSMISSION LINES The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation emitted or absolved. The electromagnetic spectrum extends from below the low frequencies used for modern radio communication to gamma radiation at the short-wavelength (high-frequency) end, thereby covering wavelengths from thousands of kilometers down to a fraction of the size of an atom as shown in Fig 1.1. The limit for long wavelengths is beyond one‟s imagination. One theory existing depicts that the short wavelength limit is in the vicinity of the Planck length. A few scientists do believe that the spectrum is infinite and continuous. Microwaves region forms a small part of the entire electromagnetic spectrum as shown in Fig 1.1. Microwaves are electromagnetic waves generally in the frequency range of 1 G Hz to 300 GHz. However with the advent of technology usage of higher end of the frequencies became possible and now the range is extended almost to 1000 G Hz. Fig:1.1: Electromagnetic Spectrum 1 Brief history of Microwaves • Modern electromagnetic theory was formulated in 1873 by James Clerk Maxwell, a German scientist solely from mathematical considerations. • Maxwell‟s formulation was cast in its modern form by Oliver Heaviside, during the period 1885 to 1887. • Heinrich Hertz, a German professor of physics carried out a set of experiments during 1887-1891 that completely validated Maxwell‟s theory of electromagnetic waves. • It was only in the 1940‟s (World War II) that microwave theory received substantial interest that led to radar development. • Communication systems using microwave technology began to develop soon after the birth of radar.
    [Show full text]
  • Transmission Lines TEM Waves
    Tele 2060 Transmission Lines • Transverse Electromagnetic (TEM) Waves • Structure of Transmission Lines • Lossless Transmission Lines Martin B.H. Weiss Transmission of Electromagnetic Energy - 1 University of Pittsburgh Tele 2060 TEM Waves • Definition: A Wave in which the Electric Field, the Magnetic Field, and the Propogation Direction are Orthogonal Use the “Right Hand Rule” to Determine Relative Orientation Thumb of Right Hand Indicates Direction of Propagation Curved Fingers of Right Hand Indicates the Direction of the Magnetic Field The Electric Field is Orthogonal ω β • Electric Field: e(t,x) = Emaxsin( t- x) V/m ω β • Magnetic Field: h(t,x) = Hmaxsin( t- x) A/m β=2π/λ ω=2πf=2π/T x is Distance Martin B.H. Weiss Transmission of Electromagnetic Energy - 2 University of Pittsburgh Tele 2060 TEM Waves λ • Note that =vp/f Same as Distance = (Speed * Time) in Physics vp is the Phase Velocity In Free Space, vp=c, the Speed of Light ==E µε • Wave Impedance: Z0 H = 1 • Phase Velocity: vp µε Martin B.H. Weiss Transmission of Electromagnetic Energy - 3 University of Pittsburgh Tele 2060 Transmission Constants • Electric Permittivity of the Transmission Medium (ε) ε = ε ε r 0 Where ε is r The Relative Permittivity Also the Dielectric Constant Typically Between 1 and 5 -12 ε = 8.85*10 (Farads/meter) 0 • Magnetic Permeability of the Transmission Medium (µ) µ=µ µ r 0 Where µ is the Relative Permeability r -7 µ = 4 *10 Henry/meter 0 Martin B.H. Weiss Transmission of Electromagnetic Energy - 4 University of Pittsburgh Tele 2060 Model of a Transmission Line L∆xR∆x ii-∆i ∆i v C∆xG∆xv-∆v ∆x Martin B.H.
    [Show full text]
  • The Design and Analysis of a Microstrip Line Which Utilizes
    THE DESIGN AND ANALYSIS OF A MICROSTRIP LINE WHICH UTILIZES CAPACITIVE GAPS AND MAGNETIC RESPONSIVE PARTICLES TO VARY THE REACTANCE OF THE SURFACE IMPEDANCE A Thesis Submitted to the Graduate Faculty of the North Dakota State University of Agriculture and Applied Science By Jerika Dawn Cleveland In Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE Major Department: Electrical and Computer Engineering April 2019 Fargo, North Dakota North Dakota State University Graduate School Title THE DESIGN AND ANALYSIS OF A MICROSTRIP LINE WHICH UTILIZES CAPACITIVE GAPS AND MAGNETIC RESPONSIVE PARTICLES TO VARY THE REACTANCE OF THE SURFACE IMPEDANCE By Jerika Dawn Cleveland The Supervisory Committee certifies that this disquisition complies with North Dakota State University’s regulations and meets the accepted standards for the degree of MASTER OF SCIENCE SUPERVISORY COMMITTEE: Dr. Benjamin D. Braaten Chair Dr. Daniel L. Ewert Dr. Jeffery Allen Approved: April 26, 2019 Dr. Benjamin D. Braaten Date Department Chair ABSTRACT This thesis presents the work of using magnetic responsive particles as a method to manipulate the surface impedance reactance of a microstrip line containing uniform capacitive gaps and cavities containing the particles. In order to determine the transmission line’s surface impedances created by each gap and particle containing cavities, a sub-unit cell that centers the gap and cavities was used. Shown in simulation, the magnetic responsive particles can then be manipulated to increase or decrease the reactance of the surface impedance based on the strength of the magnetic field present. The sub-unit cell with the greatest reactance change was then implemented into a unit cell, which is a cascade of sub-unit cells.
    [Show full text]
  • Fields, Waves and Transmission Lines Fields, Waves and Transmission Lines
    Fields, Waves and Transmission Lines Fields, Waves and Transmission Lines F. A. Benson Emeritus Professor Formerly Head of Department Electronic and Electrical Engineering University of Sheffield and T. M. Benson Senior Lecturer Electrical and Electronic Engineering University of Nottingham IUI11 SPRINGER-SCIENCE+BUSINESS MEDIA, B. V. First edition 1991 © 1991 F. A. Benson and T. M. Benson Originally published by Chapman & Hali in 1991 0412 363704 o 442 31470 1 (USA) Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the UK Copyright Designs and Patents Act, 1988, this publication may not be reproduced, stored, or transmitted, in any form or by any means, without the prior permission in writing of the publishers, or in the case of reprographic reproduction only in accordance with the terms of the licences issued by the Copyright Licensing Agency in the UK, or in accordance with the terms of licences issued by the appropriate Reproduction Rights Organization outside the UK. Enquiries concerning reproduction outside the terms stated here should be sent to the publishers at the London address printed on this page. The publisher makes no representation, express or implied, with regard to the accuracy of the informaton contained in this book and cannot accept any legal responsibility or liability for any errors or omissions that may be made. A catalogue record for this book is available from the British Library Library of Congress Cataloging-in-Publication data Benson, F. A. (Frank Atkinson), 1921- Fields, waves, and transmission lines/F. A. Benson and T.
    [Show full text]
  • Impedance Matching of a Microstrip Antenna
    (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 8, No. 7, 2017 Impedance Matching of a Microstrip Antenna Sameh Khmailia Sabri Jmal Dept. of Physics Dept. of Physics El Manar University, Faculty of Sciences El Manar University, Faculty of Sciences Tunis, Tunisia Tunis, Tunisia Hichem Taghouti Abdelkader Mami Dept. of Physics Dept. of Physics El Manar University, Faculty of Sciences El Manar University, Faculty of Sciences Tunis, Tunisia Tunis, Tunisia Abstract—Microstrip patch antennas play a very significant technique. This method is based on the principle of causality role in communication systems. In recent years, the study to of bond graph and the “L” matching network and permits to improve their performances has made great progression, and improve the impedance matching of a rectangular microstrip different methods have been proposed to optimize their antenna. characteristics such as the gain, the bandwidth, the impedance matching and the resonance frequency. Firstly, we will present the notion of impedance matching This paper presents a new method that allows to ameliorate and its different methods. the impedance matching, thus to increase the gain of a After that, we will choose the “L” matching network as the rectangular microstrip antenna. This method is based on the adaptation technique using a best method for improving the impedance matching and the simple “L” matching network. gain of a microstrip antenna. The originality of this work is the exploitation of the principle The principle of causality of bond graph will be exploited of causality that permits to detect the problems of reflected waves to detect the reflected waves and to deduce the appropriate and to obtain the suitable placement of components that structure of the “L” matching network.
    [Show full text]