Quantum Walled Brauer Algebra: Commuting Families, Baxterization, and Representations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Genetic Databases
Stefano Lonardi March, 2000 Compression of Biological Sequences by Greedy Off-line Textual Substitution Alberto Apostolico Stefano Lonardi Purdue University Università di Padova Genetic Databases § Massive § Growing exponentially Example: GenBank contains approximately 4,654,000,000 bases in 5,355,000 sequence records as of December 1999 Data Compression Conference 2000 1 Stefano Lonardi March, 2000 DNA Sequence Records Composed by annotations (in English) and DNA bases (on the alphabet {A,C,G,T,U,M,R,W,S,Y,K,V,H,D,B,X,N}) >RTS2 RTS2 upstream sequence, from -200 to -1 TCTGTTATAGTACATATTATAGTACACCAATGTAAATCTGGTCCGGGTTACACAACACTT TGTCCTGTACTTTGAAAACTGGAAAAACTCCGCTAGTTGAAATTAATATCAAATGGAAAA GTCAGTATCATCATTCTTTTCTTGACAAGTCCTAAAAAGAGCGAAAACACAGGGTTGTTT GATTGTAGAAAATCACAGCG >MEK1 MEK1 upstream sequence, from -200 to -1 TTCCAATCATAAAGCATACCGTGGTYATTTAGCCGGGGAAAAGAAGAATGATGGCGGCTA AATTTCGGCGGCTATTTCATTCATTCAAGTATAAAAGGGAGAGGTTTGACTAATTTTTTA CTTGAGCTCCTTCTGGAGTGCTCTTGTACGTTTCAAATTTTATTAAGGACCAAATATACA ACAGAAAGAAGAAGAGCGGA >NDJ1 NDJ1 upstream sequence, from -200 to -1 ATAAAATCACTAAGACTAGCAACCACGTTTTGTTTTGTAGTTGAGAGTAATAGTTACAAA TGGAAGATATATATCCGTTTCGTACTCAGTGACGTACCGGGCGTAGAAGTTGGGCGGCTA TTTGACAGATATATCAAAAATATTGTCATGAACTATACCATATACAACTTAGGATAAAA ATACAGGTAGAAAAACTATA Problem Textual compression of DNA data is difficult, i.e., “standard” methods do not seem to exploit the redundancies (if any) inherent to DNA sequences cfr. C.Nevill-Manning, I.H.Witten, “Protein is incompressible”, DCC99 Data Compression Conference 2000 2 Stefano Lonardi March, 2000 -

ARC-LEAP User Instructions for The
ARC-LEAP User Instructions Appalachian Regional Commission Local Economic Assessment Package prepared for the Appalachian Regional Commission prepared by Economic Development Research Group, Inc. Glen Weisbrod Teresa Lynch Margaret Collins January, 2004 ARC-LEAP User Instructions Appalachian Regional Commission Local Economic Assessment Package prepared for the Appalachian Regional Commission prepared by Economic Development Research Group, Inc. 2 Oliver Street, 9th Floor, Boston, MA 02109 Telephone 617.338.6775 Fax 617.338.1174 e-mail [email protected] Website www.edrgroup.com January, 2004 ARC-LEAP User Instructions PREFACE LEAP is a software tool that was designed and developed by Economic Development Research Group, Inc. (www.edrgroup.com) to assist practitioners in evaluating local economic development needs and opportunities. ARC-LEAP is a version of this tool developed specifically for the Appalachian Regional Commission (ARC) and it’s Local Development Districts (LDDs). Development of this user guide was funded by ARC as a companion to the ARC-LEAP analysis system. This document presents user instructions and technical documentation for ARC-LEAP. It is organized into three parts: I. overview of the ARC-LEAP tool II. instructions for users to obtain input information and run the analysis model III. interpretation of output tables . A separate Handbook document provides more detailed discussion of the economic development assessment process, including analysis of local economic performance, diagnosis of local strengths and weaknesses, and application of business opportunity information for developing an economic development strategy. Economic Development Research Group i ARC-LEAP User Instructions I. OVERVIEW The ARC-LEAP model serves to three related purposes, each aimed at helping practitioners identify target industries for economic development. -

Sequence Alignment/Map Format Specification
Sequence Alignment/Map Format Specification The SAM/BAM Format Specification Working Group 3 Jun 2021 The master version of this document can be found at https://github.com/samtools/hts-specs. This printing is version 53752fa from that repository, last modified on the date shown above. 1 The SAM Format Specification SAM stands for Sequence Alignment/Map format. It is a TAB-delimited text format consisting of a header section, which is optional, and an alignment section. If present, the header must be prior to the alignments. Header lines start with `@', while alignment lines do not. Each alignment line has 11 mandatory fields for essential alignment information such as mapping position, and variable number of optional fields for flexible or aligner specific information. This specification is for version 1.6 of the SAM and BAM formats. Each SAM and BAMfilemay optionally specify the version being used via the @HD VN tag. For full version history see Appendix B. Unless explicitly specified elsewhere, all fields are encoded using 7-bit US-ASCII 1 in using the POSIX / C locale. Regular expressions listed use the POSIX / IEEE Std 1003.1 extended syntax. 1.1 An example Suppose we have the following alignment with bases in lowercase clipped from the alignment. Read r001/1 and r001/2 constitute a read pair; r003 is a chimeric read; r004 represents a split alignment. Coor 12345678901234 5678901234567890123456789012345 ref AGCATGTTAGATAA**GATAGCTGTGCTAGTAGGCAGTCAGCGCCAT +r001/1 TTAGATAAAGGATA*CTG +r002 aaaAGATAA*GGATA +r003 gcctaAGCTAA +r004 ATAGCT..............TCAGC -r003 ttagctTAGGC -r001/2 CAGCGGCAT The corresponding SAM format is:2 1Charset ANSI X3.4-1968 as defined in RFC1345. -

Official Service Contractor for The2018 International Bluegrass Music Association
International Bluegrass Musical Association OFFICIAL SERVICE September 26 - 29, 2018 CONTRACTOR Raleigh Convention Center Hall C Raleigh, NC Information and Order Forms Table of Contents General Information General Information................................................................2, 3 Payment Policy & Credit Card Authorization.........................4 Third Party Billing & Credit Card Charge Authorization..5,6 Color Chart for Drape, Table Skirts and Carpet...................7 Decorating Services Custom Booth Packages...........................................................8 Furnishing Rentals.......................................................................9 Mailing Address: Custom Signs and Graphics...................................................10 P. O. Box 49837 Greensboro, NC 27419 Labor Cleaning Service.........................................................................11 Street Address: Installation and Dismantle Labor............................................12 121 North Chimney Rock Road Exhibitor Appointed Contractor.........................................13,14 Greensboro, NC 27409 Material Handling Phone: (336) 315-5225 Material Handling General Information............................15,16 Fax: (336) 315-5220 Material Handling Rate Schedule and Order Form.......17,18 Shipping Labels........................................................................19 2 General 2 Information HOLLINS Exposition Services is pleased to have been selected as the Official Service Contractor for the2018 International -

Galileo Formats
Galileo Formats October 1998 edition Chapters INDEX Introduction Booking File Air Transportation Fares Cars Hotels LeisureShopper Document Production Queues Client File/TravelScreen Travel Information Miscellaneous SECURITY Sign On H/SON SON/Z217 or Sign on at own office SON/ followed by Z and a 1 to 3 character I.D.; the I.D. can be SON/ZHA initials, a number or a combination of both SON/ZGL4HA Sign on at branch agency SON/ followed by Z, own pseudo city code and a 1 to 3 character I.D. SON/Z7XX1/UMP Sign on at 4 character PCC branch agency SON/ followed by Z, own pseudo city code, second delimiter and 1 to 3 character I.D. SB Change to work area B SA/TA Change to work area A; different duty code TA (Training) SAI/ZHA Sign back into all work areas at own office SAI/ZGL4HA Sign back into all work areas at branch agency; SAI/ followed by Z, own pseudo city code and a 1 to 3 character I.D. Sign Off SAO Temporary sign out; incomplete Booking Files must be ignored or completed SOF Sign off; incomplete Booking Files must be ignored or completed SOF/ZHA Sign off override (at own office); incomplete transactions are not protected SOF/ZGL4HA Sign off override (at branch agency); incomplete transactions are not protected; SOF/ followed by Z, own pseudo city code and a 1 to 3 character I.D. SECURITY Security Profile STD/ZHA Display security profile, for sign on HA; once displayed, password may be changed SDA List security profiles created by user (second level authoriser and above) SDA/ZXXØ List security profiles associated with agency XXØ (second level authoriser and above) STD/ZXX1UMP or Display profile STD/ followed by Z, own pseudo city code, second delimiter if pseudo STD/Z7XX1/UMP city code is 4 characters and 1 to 3 character I.D. -

Arc Welding Solutions from ESAB
Arc Welding solutions from ESAB ESAB Welding & Cutting Products / esabna.com / 1.800.ESAB.123 A full line of arc welding equipment for every application, industry and environment. Arc Welding Equipment Table of Contents Description Page Description Page Process Description .....................................................2 Genuine Heliarc® Tig Torches Arc Welding Equipment Selection Guide ...................4 Heliarc Tig Torch Selection Guide ................................56 Compacts (power source with built-in wire feeder) Gas-Cooled Torches Caddy Mig C200i ............................................................6 HW-24 ...................................................................57 Migmaster™ 215 Pro/280 Pro .........................................8 HW-90 ...................................................................59 MIG, DC Power Sources, CV/CVCC HW-9 .....................................................................61 Aristo™ Mig U5000i .......................................................10 HW-17 ...................................................................63 Origo™ Mig 320/410 ......................................................12 HW-26 ...................................................................65 Origo Mig 4002c/6502c ................................................21 Water-Cooled Torches Wire Feeders - Semi-Automatic HW-20 ...................................................................67 MobileFeed™ 300AVS .....................................................15 HW-18 ...................................................................69 -

DICOM Compression 2002
The Medicine Behind the Image DDIICCOOMM CCoommpprreessssiioonn 22000022 David Clunie Director of Technical Operations Princeton Radiology Pharmaceutical Research The Medicine SScchheemmeess SSuuppppoorrtteedd Behind the Image • RLE • JPEG - lossless and lossy • JPEG-LS - more efficient, fast lossless • JPEG 2000 - progressive, ROI encoding • Deflate (zip/gzip) - for non-image objects The Medicine IInn pprraaccttiiccee mmoossttllyy …… Behind the Image • Lossless JPEG for cardiac angio – multi-frame 512x512x8, 1024x1024x10 – CD-R and on network • Lossless JPEG for CT/MR – mostly on MOD media rather than over network – 256x256 to 1024x1024, 12-16 bits • RLE/lossless/lossy JPEG for Ultrasound – 640x480 single and multiframe 8 bits gray/RGB, text The Medicine BBuutt …… Behind the Image • JPEG lossless not the most effective • JPEG lossy limited to 12 bits unsigned • Undesirable JPEG blockiness • Perception that wavelets are better • Need for better progressive encoding • Need for region-of-interest encoding The Medicine JJPPEEGG LLoosssslleessss Behind the Image • Reasonable predictive scheme – Most often only previous pixel predictor used (SV1), which is not always the best choice • No run-length mode – No way to take advantage of large background areas • Huffman entropy coder – Slow (multi-pass) The Medicine LLoosssslleessss CCoommpprreessssiioonn Behind the Image CALIC Arithmetic 3.91 JPEG2000 VM4 5x3 3.81 JPEG-LS MINE 3.81 JPEG2000 VM4 3.66 2x10 S+P Arithmetic 3.4 JPEG-LS MINE - NO 3.31 Byte All RUN NASA szip 3.09 JPEG best 3.04 JPEG SV -

On the Spectral Theorem of Langlands
On the Spectral Theorem of Langlands Patrick Delorme April 22, 2021 A` Chantal Abstract We show that the Hilbert subspace of L2pGpF qzGpAqq generated by wave packets of Eisenstein series built from discrete series is the whole space. To- gether with the work of Lapid [18], it achieves a proof of the spectral theorem of R.P. Langlands based on the work of J. Bernstein and E. Lapid [7] on the meromorphic continuation of Eisenstein series from I use truncation on compact sets as J. Arthur did for the local trace formula in [2]. 1 Introduction We denote by E the isometry introduced by E. Lapid in [18], Theorem 2, whose proof involves the meromorphic continuation of of Eisenstein series built from discrete data. A dense subspace of its image is generated by wave packets of these Eisenstein series. We show that this image is equal to L2pGpF qzGpAqq. This is what Lapid calls the second half of the proof of the spectral theorem of Langlands. It achieves a new proof of the spectral theorem of R.P. Langlands ([17], [20]). Notice that the proof of Langlands describes the spectrum as residues of Eisenstein series built from cuspidal data. arXiv:2006.12893v3 [math.RT] 21 Apr 2021 One uses the notion of temperedness of automorphic forms introduced by J. Franke [15](cf. also [21] section 4.4). We show this notion of temperedness is weaker than the notion of temperedness introduced by Joseph Bernstein in [6]. We prove that for bounded sets of unitary parameters, the Eisenstein series are uniformly tempered when the parameter is unitary and bounded. -
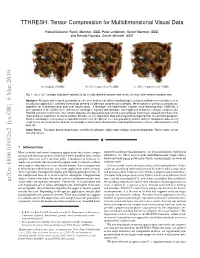
TTHRESH: Tensor Compression for Multidimensional Visual Data
TTHRESH: Tensor Compression for Multidimensional Visual Data Rafael Ballester-Ripoll, Member, IEEE, Peter Lindstrom, Senior Member, IEEE, and Renato Pajarola, Senior Member, IEEE (a) Original (512MB) (b) 10:1 compression (51.2MB) (c) 300:1 compression (1.71MB) Fig. 1. (a) a 5123 isotropic turbulence volume [1]; (b) visually identical compression result; (c) result after extreme compression. Abstract—Memory and network bandwidth are decisive bottlenecks when handling high-resolution multidimensional data sets in visualization applications, and they increasingly demand suitable data compression strategies. We introduce a novel lossy compression algorithm for multidimensional data over regular grids. It leverages the higher-order singular value decomposition (HOSVD), a generalization of the SVD to three dimensions and higher, together with bit-plane, run-length and arithmetic coding to compress the HOSVD transform coefficients. Our scheme degrades the data particularly smoothly and achieves lower mean squared error than other state-of-the-art algorithms at low-to-medium bit rates, as it is required in data archiving and management for visualization purposes. Further advantages of the proposed algorithm include very fine bit rate selection granularity and the ability to manipulate data at very small cost in the compression domain, for example to reconstruct filtered and/or subsampled versions of all (or selected parts) of the data set. Index Terms—Transform-based compression, scientific visualization, higher-order singular value decomposition, Tucker model, tensor decompositions 1 INTRODUCTION Most scientific and visual computing applications face heavy compu- support for arbitrary dimensionality, ease of parallelization, topological tational and data management challenges when handling large and/or robustness, etc. -

MRCZ – a Proposed Fast Compressed MRC File Format and Direct Detector Normalization Strategies
bioRxiv preprint doi: https://doi.org/10.1101/116533; this version posted March 13, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. MRCZ – A proposed fast compressed MRC file format and direct detector normalization strategies Robert A. McLeod1*, Ricardo Diogo Righetto1, Andy Stewart2, Henning Stahlberg1 1 Center for Cellular Imaging and NanoAnalytics (C-CINA), University of Basel, Basel, Switzerland 2 Department of Physics, University of Limerick, Limerick, Ireland * Corresponding author: Robert A. McLeod, C-CINA, Biozentrum, University of Basel ([email protected]) Abstract The introduction of high-speed CMOS detectors is fast marching the field of transmission electron microscopy into an intersection with the computer science field of big data. Automated data pipelines to control the instrument and the initial processing steps are imposing more and more onerous requirements on data transfer and archiving. We present a proposal for expansion of the venerable MRC file format to combine integer decimation and lossless compression to reduce storage requirements and improve file read/write times by >1000 % compared to uncompressed floating-point data. The integer decimation of data necessitates application of the gain normalization and outlier pixel removal at the data destination, rather than the source. With direct electron detectors, the normalization step is typically provided by the vendor and is not open- source. We provide robustly tested normalization algorithms that perform at-least as well as vendor software. -

Introduc2on to Linux
Introduc)on to Linux Geng so3ware Installing new so3ware • Downloading – wget http://<url>/file copies file to current place • Unpacking – Geng the file from the downloaded package • Compiling – Making the code into an executable program • Running – Run your new program Compressed File Extensions • bz2 - BZzip2 compressed archive file • gz - Gnu Zipped Archive File • gzip - Gnu Zipped File • tar - Consolidated Unix File Archive • tgz - Gzipped Tar File • zip - ZIP compression Geng the file out • tar xzf file.tar.gz -> file • gunzip file.gz -> file • tar xf file.tar -> file • tar xzf file.tgz -> file • tar xjf file.tar.bz2 -> file • bunzip2 file.bz2 -> file • rar x file.rar -> file • tar xjf file.tbz2 -> file • unzip file.zip -> file Compiling Normal procedure • ./configure --prefix=$HOME • make • make install To remove all but the source files • make clean Permissions • chmod - change file modes – Permissions are Read Write eXecute – People affected are User Group Others Example chmod u+xo-rwx file removes all permissions for the file file from other users and makes the file executable for the owner. Linking • In the wrong place • Too large to move or copy ln –s <source file> <target file> Redirec)on • Pung output to next program • Pung output into a file • Pung output at the end of a file (append) | > >> Part II Common file types in bioinformacs FASTA raw data • Line 1: Single line descrip)on, marked by “>” • Line 2…n: Lines of sequence data Example >gi|31563518|ref|NP_852610.1 MKMRFFSSPCGKAAVDPADRCKEVQQIRDQHPS KIPVIIERYKGEKQLPVLDKTKFLPDHVNMSEL VKIIRRRLQLNPTQAFFLLVNQHSMVSVSTPIA -

Recode: a Data Reduction and Compression Description for High Throughput Time-Resolved Electron Microscopy
ReCoDe: A Data Reduction and Compression Description for High Throughput Time-Resolved Electron Microscopy 1,2 1,2 1,2 3 1,2,4 1,2 1,2 Abhik Datta , Kian Fong Ng , Balakrishnan Deepan , Melissa Ding , See Wee Chee , Yvonne Ban , Jian Shi , Duane Loh1,2,4 1 Centre for BioImaging Sciences, National University of Singapore, Singapore 117557. 2 Department of Biological Sciences, National University of Singapore, Singapore 117557. 3 Department of Computer Science and Engineering, Ohio State University, Columbus, OH 43210, USA. 4 Department of Physics, National University of Singapore, Singapore 117551. Abstract Fast, direct electron detectors have significantly improved the spatio-temporal resolution of electron microscopy movies. Preserving both spatial and temporal resolution in extended observations, however, requires storing prohibitively large amounts of data. Here, we describe an efficient and flexible data reduction and compression scheme (ReCoDe) that retains both spatial and temporal resolution by preserving individual electron events. Running ReCoDe on a workstation we demonstrate on-the-fly reduction and compression of raw data streaming off a detector at 3 GB/s, for hours of uninterrupted data collection. The output was 100-fold smaller than the raw data and saved directly onto network-attached storage drives over a 10 GbE connection. We discuss calibration techniques that support electron detection and counting (e.g. estimate electron backscattering rates, false positive rates, and data compressibility), and novel data analysis methods enabled by ReCoDe (e.g. recalibration of data post acquisition, and accurate estimation of coincidence loss). Introduction Fast, back-thinned direct electron detectors are rapidly transforming electron microscopy.