DOCSLIB.ORG

Accelerator-Based Production of High Specific Activity Radionuclides for Radiopharmaceutical Applications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Accelerator-Based Production of High Specific Activity Radionuclides for Radiopharmaceutical Applications ACCELERATOR-BASED PRODUCTION OF HIGH SPECIFIC ACTIVITY RADIONUCLIDES FOR RADIOPHARMACEUTICAL APPLICATIONS A Dissertation Presented to the Faculty of the Graduate School at the University of Missouri-Columbia In Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy By MATTHEW DAVID GOTT Dr. Silvia S. Jurisson, Dissertation Advisor Dr. Cathy S. Cutler, Co-Advisor JULY 2015 The undersigned, appointed by the dean of the Graduate School, have examined the dissertation entitled ACCELERATOR-BASED PRODUCTION OF HIGH SPECIFIC ACTIVITY RADIONUCLIDES FOR RADIOPHARMACEUTICAL APPLICATIONS presented by Matthew David Gott, a candidate for the degree of Doctor of Philosophy, and hereby certify that, in their opinion, it is worthy of acceptance. Dr. Silvia S. Jurisson Dr. Cathy S. Cutler Dr. C. Michael Greenlief Dr. J. David Robertson DEDICATION This dissertation is dedicated to my wonderful parents, David and Cathy. You have always been my greatest supporters and encouraged me every step of the way. None of this would have been possible without you. ACKNOWLEDGMENTS I would like to thank Dr. C. Michael Greenlief and Dr. J. David Roberston for serving on my committee and providing advice throughout this process. I would like to thank all of my collaborators who provided assistance and guidance throughout this project. Dr. Donald Wycoff, Dr. Anthony Degraffenreid, and Yutian Feng were instrumental in the arsenic production work. Dr. Alan Ketring, Dr. John Lydon, Mary Embree, Stacy Wilder, Alex Saale, Melissa Evans-Blumer, and the staff at the University of Missouri Research Reactor provided support and ideas for experimental work throughout this dissertation. Dr. Michael Fassbender, Dr. Beau Ballard, and the members of the C-IIAC group at Los Alamos National Laboratory provided assistance and guidance with the experimental work for the W/Re separation method. Dr. D. Scott Wilbur, Dr. Ethan Balkin, Bennett Smith, and the members of the accelerator group at the University of Washington provided assistance and ideas for the experimental work for the osmium, tungsten, and germanium targetry. Dr. Suzanne Smith, Chris Cullen, and the members of the MIRP group at Brookhaven National Laboratory provided assistance and guidance with the experimental work for the osmium, tungsten, and arsenide irradiations and separations. Lauren Radford, Kimberly Reining, Dr. David Rotsch, Dr. Dustin Demoin, and Dr. Jurisson’s research group provided help throughout the project by providing ideas, support, training, and revising presentations and publications. ii TABLE OF CONTENTS ACKNOWLEDGMENTS .................................................................................................. ii TABLE OF CONTENTS ................................................................................................... iii LIST OF FIGURES ......................................................................................................... viii LIST OF TABLES ............................................................................................................ xii ACADEMIC ABSTRACT ............................................................................................. xvii Chapter 1: Introduction ....................................................................................................... 1 1.1 Basics of Radiopharmaceuticals ............................................................................... 1 1.2 Modes of Radioactive Decay Commonly Used for Radiopharmaceutical Drugs .... 2 1.2.1 Alpha Decay....................................................................................................... 3 1.2.2 Beta Decay ......................................................................................................... 5 1.2.3 Positron Emission .............................................................................................. 8 1.2.4 Isomeric Transition and Electron Capture (Gamma Emitters) ........................ 10 1.3 Isotope Production .................................................................................................. 13 1.3.1 Production of Radionuclides in Reactors ......................................................... 15 1.3.2 Production of Radionuclides in an Accelerator ............................................... 16 1.3.3 Basics of Targetry ............................................................................................ 17 1.3.4 Basics of Separation ......................................................................................... 18 Chapter 2: Production of 186Re ......................................................................................... 21 2.1 186Re Production via Proton Bombardment of Osmium Targets ............................ 22 iii 2.1.1 Materials and Methods ..................................................................................... 22 2.1.2 Results and Discussion .................................................................................... 29 2.1.3 Conclusions ...................................................................................................... 39 2.1.4 Future Studies .................................................................................................. 39 2.2 186Re Production via Proton Bombardment of Tungsten Targets ........................... 40 2.2.1 Materials and Methods ..................................................................................... 40 2.2.2 Results and Discussion .................................................................................... 50 2.2.3 Conclusions ...................................................................................................... 73 2.2.4 Future Studies .................................................................................................. 74 Chapter 3: Production of 72,77As ....................................................................................... 75 3.1 Production of 72As from the Decay of Accelerator Produced 72Se ......................... 75 3.1.1 Materials and Methods ..................................................................................... 76 3.1.2 Results and Discussion .................................................................................... 83 3.1.3 Conclusions ...................................................................................................... 88 3.1.4 Future Studies .................................................................................................. 89 3.2 Production of 77As from the Decay of Reactor Produced 77Ge .............................. 90 3.2.1 Materials and Methods ..................................................................................... 90 3.2.2 Results and Discussion .................................................................................... 97 3.2.3 Conclusions .................................................................................................... 104 3.2.4 Future Studies ................................................................................................ 105 iv Chapter 4: Production of Other Radiopharmaceutical Isotopes ..................................... 107 44,44m 4.1 Production of Sc via Proton Bombardment of CaCO3 ................................. 107 4.1.1 Methods and Materials ................................................................................... 107 4.1.2 Results and Discussion .................................................................................. 111 4.1.3 Conclusions .................................................................................................... 114 4.1.4 Future Studies ................................................................................................ 114 99m 4.2 Production of Tc via Proton and Deuteron Bombardment of MoS2 ................ 115 4.2.1 Methods and Materials ................................................................................... 115 4.2.2 Results and Discussion .................................................................................. 118 4.2.3 Conclusions .................................................................................................... 123 4.2.4 Future Studies ................................................................................................ 123 REFERENCES ............................................................................................................... 124 Appendix A: Production Calculations ............................................................................ 134 A.1 Discussion of Target Cross Sections .................................................................... 134 A.1.1 Proton Bombardment of Osmium via natOs(p, x) reactions .......................... 135 A.1.2 Proton Bombardment of Tungsten via natW(p, xn)Re reactions ................... 136 A.1.3 Alpha Bombardment of Germanium via natGe(a, x) reactions ...................... 138 A.1.4 Proton Bombardment of Arsenic via 75As(p, 4n)72Se reactions.................... 139 A.1.5 Proton Bombardment of Calcium via natCa(p, xn)Sc reactions..................... 140 A.1.6 Proton Bombardment of Molybdenum via natMo(p, xn) reactions ............... 141 v A.1.7 Deuteron Bombardment of Molybdenum via natMo(d, xn) reactions ........... 143 A.2 SRIM Calculations for Targets ............................................................................ 145 A.2.1 Osmium Metal Target ................................................................................... 147 A.2.2
Load more

Recommended publications
  • High Accuracy Measurement of Isotope Ratios of Molybdenum in Some Terrestrial Molybdenites
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector ARTICLES High Accuracy Measurement of Isotope Ratios of Molybdenum in Some Terrestrial Molybdenites Qi-Lu* and Akimasa Masuda Department of Chemistry, Faculty of Science, The University of Tokyo, Tokyo, Japan The isotope ratios of molybdenum in molybdenites were studied. A special triple filament technique was used to obtain stable and lasting signals for MO+. There are no differences bigger than ~0.4 parts per IO4 among four samples and the standard. CJ Am Sot Mass Spectrom 1992, 3, IO- 17) olybdenum is a very interesting element be- denum thus far, in spite of the potential importance cause its seven isotopes can reflect several of research in isotopic abundance of molybdenum. M effects related to nuclear physics. The nu- In this study we have established a method for clear phenomena that may affect the isotope ratios in securing stable and lasting current of MO+ and exam- question are (1) the synthesis of seven isotopes of MO ined the mass fractionation of MO isotopes during involving three processes (r, s, and p) in the standard measurement. Based on these studies, the isotope model of nucleosynthesis [I]; ($2 the nuclear hssion of ratios of MO were determined with high precision uranium-238, which produces MO, “MO, 98Mo, and for some molybdenites from a variety of locations ‘“MO; and (3) the double-beta decays of ‘“Zr and throughout the world. The present study will afford a lwMo leading to 96Mo and ‘“Ru. Another intriguing foundation for further precise studies of molybdenum property of this element is that the anomalous abun- isotopes involving meteorites and terrestrial rocks.
    [Show full text]
  • The Separation and Determination of Osmium and Ruthenium
    Louisiana State University LSU Digital Commons LSU Historical Dissertations and Theses Graduate School 1969 The epS aration and Determination of Osmium and Ruthenium. Harry Edward Moseley Louisiana State University and Agricultural & Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_disstheses Recommended Citation Moseley, Harry Edward, "The eS paration and Determination of Osmium and Ruthenium." (1969). LSU Historical Dissertations and Theses. 1559. https://digitalcommons.lsu.edu/gradschool_disstheses/1559 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Historical Dissertations and Theses by an authorized administrator of LSU Digital Commons. For more information, please contact [email protected]. ThU dissertation has been 69-17,123 microfilmsd exactly as received MOSELEY, Harry Edward, 1929- THE SEPARATION AND DETERMINATION OF OSMIUM AND RUTHENIUM. Louisiana State University and Agricultural and Mechanical College, PhJ>., 1969 Chemistry, analytical University Microfilms, Inc., Ann Arbor, Michigan THE SEPARATION AND DETERMINATION OF OSMIUM AND RUTHENIUM A Dissertation Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Philosophy in The Department of Chemistry Harry Edward Moseley B.S., Lpuisiana State University, 1951 M.S., Louisiana State University, 1952 J anuary, 1969 ACKNOWLEDGMENTS Thanks are due to Dr. Eugene W. Berg under whose direction this work was performed, to Dr. A. D. Shendrikar for his help in the tracer studies, and to Mr. J. H. R. Streiffer for his help in writing the com­ puter program.
    [Show full text]
  • Isotope Production Potential at Sandia National Laboratories: Product, Waste, Packaging, and Transportation*
    Isotope Production Potential at Sandia National Laboratories: Product, Waste, Packaging, and Transportation* A. J. Trennel Transportation Systems Department *- *-, o / /"-~~> Sandia National Laboratories** ' J Albuquerque, NM 87185 O Q T » Abstract The U.S. Congress directed the U.S. Department of Energy to establish a domestic source of molybdenum-99, an essential isotope used in nuclear medicine and radiopharmacology. An Environmental Impact Statement for production of 99Mo at one of four candidate sites is being prepared. As one of the candidate sites, Sandia National Laboratories is developing the Isotope Production Project. Using federally approved processes and procedures now owned by the U.S. Department of Energy, and existing facilities that would be modified to meet the production requirements, the Sandia National Laboratories' Isotope Project would manufacture up to 30 percent of the U.S. market, with the capacity to meet 100 percent of the domestic need if necessary. This paper provides a brief overview of the facility, equipment, and processes required to produce isotopes. Packaging and transportation issues affecting both product and waste are addressed, and the storage and disposal of the four low-level radioactive waste types generated by the production program are considered. Recommendations for future development are provided. This work was performed at Sandia National Laboratories, Albuquerque, New Mexico, for the U.S. Department of Energy under Contract DE-AC04-94AL85000. A U.S. Department of Energy facility. DISTRPJTO OF THIS DOCUMENT IS UNLIMITED #t/f W A8 1 fcll PROJECT NEED AND BACKGROUND Nuclear medicine is an expanding segment of today's medical and pharmaceutical communities. Specific radioactive isotopes are vital, with molybdenum-99 (99Mo) being the most important medical isotope.
    [Show full text]
  • Cosmogenic Production As a Background in Searching For
    Cosmogenic Production as a Background in Searching for Rare Physics Processes D.-M. Mei a , Z.-B. Yin a,b,c,1, S. R. Elliott d aDepartment of Physics, The University of South Dakota, Vermillion, South Dakota 57069 bInstitute of Particle Physics, Huazhong Normal University, Wuhan 430079, China cKey Laboratory of Quark & Lepton Physics (Huazhong Normal University), Ministry of Education, China dLos Alamos National Laboratory, Los Alamos, New Mexico 87545 Abstract We revisit calculations of the cosmogenic production rates for several long-lived iso- topes that are potential sources of background in searching for rare physics processes such as the detection of dark matter and neutrinoless double-beta decay. Using up- dated cosmic-ray neutron flux measurements, we use TALYS 1.0 to investigate the cosmogenic activation of stable isotopes of several detector targets and find that the cosmogenic isotopes produced inside the target materials and cryostat can result in large backgrounds for dark matter searches and neutrinoless double-beta decay. We use previously published low-background HPGe data to constrain the production of 3H on the surface and the upper limit is consistent with our calculation. We note that cosmogenic production of several isotopes in various targets can generate po- arXiv:0903.2273v1 [nucl-ex] 12 Mar 2009 tential backgrounds for dark matter detection and neutrinoless double-beta decay with a massive detector, thus great care should be taken to limit and/or deal with the cosmogenic activation of the targets. Key words: Cosmogenic activation, Dark matter detection, Double-beta decay PACS: 13.85.Tp, 23.40-s, 25.40.Sc, 28.41.Qb, 95.35.+d, 29.40.Wk Email address: [email protected] (D.-M.
    [Show full text]
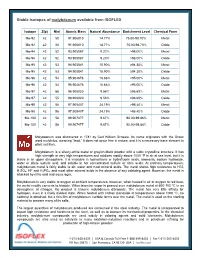
  • Stable Isotopes of Molybdenum Available from ISOFLEX
    Stable isotopes of molybdenum available from ISOFLEX Isotope Z(p) N(n) Atomic Mass Natural Abundance Enrichment Level Chemical Form Mo-92 42 50 91.906810 14.77% 75.00-98.70% Metal Mo-92 42 50 91.906810 14.77% 75.00-98.70% Oxide Mo-94 42 52 93.905087 9.23% >98.00% Metal Mo-94 42 52 93.905087 9.23% >98.00% Oxide Mo-95 42 53 94.905841 15.90% ≥94.30% Metal Mo-95 42 53 94.905841 15.90% ≥94.30% Oxide Mo-96 42 54 95.904678 16.68% >95.00% Metal Mo-96 42 54 95.904678 16.68% >95.00% Oxide Mo-97 42 55 96.906020 9.56% ≥96.60% Metal Mo-97 42 55 96.906020 9.56% ≥96.60% Oxide Mo-98 42 56 97.905407 24.19% >98.40% Metal Mo-98 42 56 97.905407 24.19% >98.40% Oxide Mo-100 42 58 99.907477 9.67% 90.00-99.86% Metal Mo-100 42 58 99.907477 9.67% 90.00-99.86% Oxide Molybdenum was discovered in 1781 by Carl William Scheele. Its name originates with the Greek word molybdos, meaning “lead.” It does not occur free in nature, and it is a necessary trace element in plant nutrition. Molybdenum is a silvery-white metal or grayish-black powder with a cubic crystalline structure. It has high strength at very high temperatures and oxidizes rapidly above 1000 °F in air at sea level, but it is stable in an upper atmosphere.
    [Show full text]
  • PSI • Scientific Report 1999 /Volume I
    CH0000002 PAUL SCHERRER INSTITUT ISSN 1423-7296 March 2000 PSI • Scientific Report 1999 /Volume I Particles and Matter 3 1/28 An international collaboration of radiochemists led by the Laboratory for Radiochemistry and Environmental Chemistry of PSl and Bern University succeeded for the first time to experimentally investigate the chemical properties of bohrium (element 107) and to establish it as a member of group 7 of the Periodic Table. During a one-month long experiment, a total of only six bohrium atoms were gaschromatographically isolated in the form of volatile bohrium oxychloride molecules and identified by registering their unique decay sequence of alpha particle emissions via dubnium (element 105) to lawrencium (element 103). The short-lived bohrium atoms, decaying with a half-life of about 20 s, were produced by bombarding a very rare, highly radioactive berkelium target supplied by the US department of energy with an intense beam of neon ions at the PSl injector 1 cyclotron. PAUL SCHERRER INSTITUT ISSN 1423-7296 March 2000 \} Scientific Report 1999 Volume I Particles and Matter ed. by: J. Gobrecht, H. Gaggeler, D. Herlach, K. Junker, P.-R. Kettle, P. Kubik, A. Zehnder CH-5232 Villigen PSI Switzerland Telephone:+41 56 310 21 11 Telefax:+ 41 56 310 21 99 http://www.psi.ch TABLE OF CONTENTS Introduction .1 Laboratory for Particle Physics 3 Foreword 4 Particle Physics Theory Theory (I) 5 Theory (II) 6 Ring Accelerator Experiments Particle Properties and Decays A precise measurement of the Jt+-^7t°e+v decay rate 7 Measurement of
    [Show full text]
  • Molybdenum in the Open Cluster Stars
    MOLYBDENUM IN THE OPEN CLUSTER STARS T. Mishenina1, E. Shereta1, M. Pignatari2,3,6,7, G. Carraro4, T. Gorbaneva1, C. Soubiran5 1Astronomical Observatory, Odessa National University, Marazlievskaia Str., 1V, 65014, Odessa, Ukraine [email protected] 2 E.A. Milne Centre for Astrophysics, Department of Physics & Mathematics, University of Hull, HU6 7RX, United Kingdom [email protected] 3 Konkoly Observatory, Hungarian Academy of Sciences, Konkoly Thege Miklos ut 15-17, H-1121 Budapest, Hungary 4 Dipartimento di Fisica e Astronomia, Universita di Padova, I-35122, Padova, Italy [email protected] 5 Laboratoire d’astrophysique de Bordeaux, Universit´eBordeaux, CNRS, B18N, all´ee Geoffroy Saint-Hilaire, 33615 Pessac, France [email protected] 6 Joint Institute for Nuclear Astrophysics - Center for the Evolution of the Elements, USA 7 NuGrid Collaboration https://nugrid.github.io/ June 9, 2020 arXiv:2006.04629v1 [astro-ph.GA] 8 Jun 2020 Abstract Molybdenum abundances in the stars from 13 different open clusters were determined. High-resolution stellar spectra were obtained using the VLT tele- scope equipped with the UVES spectrograph on Cerro Paranal, Chile. The Mo abundances were derived in the LTE approximation from the Mo I lines at 5506 A˚ and 5533 A.˚ A comparative analysis of the behaviour of molyb- denum in the sampled stars of open clusters and Galactic disc show similar trends of decreasing Mo abundances with increasing metallicities; such a be- haviour pattern suggests a common origin of the examined populations. On the other hand, the scatter of Mo abundances in the open cluster stars is slightly greater, 0.14 dex versus 0.11 dex.
    [Show full text]
  • Oxidation-Reduction Alternating Copolymerization of Germylene and N-Phenyl-P-Quinoneimine
    Polymer Journal (2015) 47, 31–36 & 2015 The Society of Polymer Science, Japan (SPSJ) All rights reserved 0032-3896/15 www.nature.com/pj ORIGINAL ARTICLE Oxidation-reduction alternating copolymerization of germylene and N-phenyl-p-quinoneimine Satoru Iwata1, Mitsunori Abe1, Shin-ichiro Shoda1 and Shiro Kobayashi1,2 The germylenes bis[bis(trimethylsilyl)amido]germanium (1a) and bis[t-butyl-trimethylsilyl]amido]germanium (1b) were reacted with N-phenyl-p-quinoneimine (2) to give copolymers (3a and 3b) with alternating tetravalent germanium and p-aminophenol units. The copolymerization took place smoothly at 0 °C without added catalyst or initiator. 1 acted as a reductant monomer, and 2 acted as an oxidant monomer (oxidation-reduction alternating copolymerization). Product copolymers were obtained in very high yields and had high molecular weights. The copolymers were soluble in toluene, benzene, n-hexane and chloroform, whereas they were insoluble in acetonitrile and acetone. Additionally, they were stable toward hydrolytic degradation. Electron spin resonance (ESR) spectroscopic studies of the reaction suggested a structure of a stable germyl radical and a plausible mechanism of biradical copolymerization. Polymer Journal (2015) 47, 31–36; doi:10.1038/pj.2014.84; published online 8 October 2014 INTRODUCTION investigations.10 Five- and six-membered cyclic germylenes, conver- Divalent germanium compounds (germylenes) and their tin analogs sely, were copolymerized with p-benzoquinone derivatives in similar (stannylenes) continue to attract
    [Show full text]
  • PRODUCTION of Mo-99/Tc-99M VIA PHOTONEUTRON REACTION USING
    PRODUCTION OF Mo-99/Tc-99m VIA PHOTONEUTRON REACTION USING NATURAL MOLYBDENUM A Thesis by TALAL BADER HARAHSHEH Submitted to the Office of Graduate and Professional Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Chair of Committee, Gamal Akabani Co-Chair of Committee, John W. Poston, Sr. Committee Member, Victor M. Ugaz Head of Department, Yassin A. Hassan May 2017 Major Subject: Nuclear Engineering Copyright 2017 Talal Harahsheh ABSTRACT The current shortage of the widely used radionuclide 99mTc has raised many concerns in the nuclear medicine industry. The shortage is caused by the outdated method of production using highly enriched uranium (HEU) and nuclear reactors. This production method is no longer feasible due to the restrictions on the use of HEU. Alternative methods of production must be addressed to ensure the uninterrupted supply of this key radionuclide. This research analyzes an alternative production method of 99mTc using an accelerator-generated 99Mo, which is the parent element of 99mTc. The radionuclide 99mTc has a short half-life of 6 hours. However, 99Mo, the parent nuclide has a much longer half-life of 66 hours. Usually, a medical facility receives a 99Mo/99mTc generator. Technetium-99m would be obtained from the 99Mo provided through chemical separation, which is conducted at the medical facilities. The main issues to be addressed include the production of 99Mo using the photonuclear reaction, the containment and exclusion of unwanted decay products, ensuring the integrity of the end-product 99Mo/99mTc post chemical separation, and assessing the economic feasibility of the complete strategy, including life cycle.
    [Show full text]
  • Jahresbericht 2007
    IKMz 2008- 1 ISSN 0932-7622 INSTITUT FÜR KERNCHEMIE UNIVERSITÄT MAINZ JAHRESBERICHT 2007 August 2008 FRITZ-STRASSMANN-WEG 2, D-55128 MAINZ, TELEFON (06131) 3925879, TELEFAX (06131) 3925253 Kernchemie im Internet Das Institut für Kernchemie der Universität Mainz ist mit einer Homepage im World Wide Web vertreten. Unter der Adresse http://www.kernchemie.uni-mainz.de finden Sie aktuelle Informationen zum Institut, seinen Mitarbeitern, den Lehrveranstaltungen und den Forschungsaktivitäten. Die in diesem Bericht vorgelegten Ergebnisse stammen zum Teil aus noch nicht abgeschlossenen Arbeiten und sind daher als vorläufige Mitteilung zu bewerten. INSTITUT FÜR KERNCHEMIE UNIVERSITÄT MAINZ JAHRESBERICHT 2007 Herausgeber: Frank Rösch Mainz, im August 2008 Vorwort Der vorliegende Jahresbericht 2007 gibt einen Überblick über die wissenschaftlichen Aktivitäten des Instituts für Kernchemie. Er legt damit gleichzeitig all denen, die uns in ideeller und finanzieller Weise gefördert haben, Rechenschaft ab über die Verwendung nicht unerheblicher öffentlicher Mittel. Außerdem beschreibt er den Status der technischen Einrichtungen des Instituts und technische Neu- entwicklungen. Schließlich stellt er die Ergebnisse des Instituts in Form von Publikationen, Konferenzbeiträgen, Dissertationen, Diplom- und Staatsexamensarbeiten sowie die Beiträge seiner Hochschullehrer in der Lehre und Weiterbildung dar. Der wissenschaftliche Bericht umfasst die drei Forschungsschwerpunkte: • Kernchemie im Sinne grundlegender Fragestellungen, • Radiopharmazeutische Chemie und Anwendung radiochemischer Methoden mit medizinischer Zielsetzung, • Hochempfindliche und –selektive Analytik für umweltrelevante, technische und biologische Probleme. Im August 2007 hat der Präsident unserer Universität, Herr Prof. Dr. Krausch, die Laufzeit des Forschungsreaktors TRIGA Mainz bis zunächst 2020 verlängert. Die Carl-Zeiss-Stiftung hat 2007 die Einrichtung einer Juniorprofessur für das Thema „Ultrakalte Neutronen“ am Institut für Kernchemie ab 2008 ermöglicht.
    [Show full text]
  • Direct Measurement of the Neutron
    Louisiana State University LSU Digital Commons LSU Doctoral Dissertations Graduate School 1-9-2020 Stellar Nucleosynthesis: Direct Measurement of the Neutron- Capture Cross Sections of Stable Germanium Isotopes and Design of a Next Generation Ion Trap for the Study of Beta- Delayed Neutron Emission Alexander Laminack Louisiana State University and Agricultural and Mechanical College Follow this and additional works at: https://digitalcommons.lsu.edu/gradschool_dissertations Part of the Instrumentation Commons, Nuclear Commons, Physical Processes Commons, and the Stars, Interstellar Medium and the Galaxy Commons Recommended Citation Laminack, Alexander, "Stellar Nucleosynthesis: Direct Measurement of the Neutron-Capture Cross Sections of Stable Germanium Isotopes and Design of a Next Generation Ion Trap for the Study of Beta- Delayed Neutron Emission" (2020). LSU Doctoral Dissertations. 5131. https://digitalcommons.lsu.edu/gradschool_dissertations/5131 This Dissertation is brought to you for free and open access by the Graduate School at LSU Digital Commons. It has been accepted for inclusion in LSU Doctoral Dissertations by an authorized graduate school editor of LSU Digital Commons. For more information, please [email protected]. STELLAR NUCLEOSYNTHESIS: DIRECT MEASUREMENT OF THE NEUTRON-CAPTURE CROSS SECTIONS OF STABLE GERMANIUM ISOTOPES AND DESIGN OF A NEXT GENERATION ION TRAP FOR THE STUDY OF β-DELAYED NEUTRON EMISSION A Dissertation Submitted to the Graduate Faculty of the Louisiana State University and Agricultural and Mechanical College in partial fulfillment of the requirements for the degree of Doctor of Philosophy in The Department of Physics and Astronomy by Alexander Laminack B. S., The Unviersity of Alabama, 2015 May 2020 To my wife and son: Kristy Allen Alexander Laminack and Daniel Allen Laminack.
    [Show full text]
  • The New Nuclear Forensics: Analysis of Nuclear Material for Security
    THE NEW NUCLEAR FORENSICS Analysis of Nuclear Materials for Security Purposes edited by vitaly fedchenko The New Nuclear Forensics Analysis of Nuclear Materials for Security Purposes STOCKHOLM INTERNATIONAL PEACE RESEARCH INSTITUTE SIPRI is an independent international institute dedicated to research into conflict, armaments, arms control and disarmament. Established in 1966, SIPRI provides data, analysis and recommendations, based on open sources, to policymakers, researchers, media and the interested public. The Governing Board is not responsible for the views expressed in the publications of the Institute. GOVERNING BOARD Sven-Olof Petersson, Chairman (Sweden) Dr Dewi Fortuna Anwar (Indonesia) Dr Vladimir Baranovsky (Russia) Ambassador Lakhdar Brahimi (Algeria) Jayantha Dhanapala (Sri Lanka) Ambassador Wolfgang Ischinger (Germany) Professor Mary Kaldor (United Kingdom) The Director DIRECTOR Dr Ian Anthony (United Kingdom) Signalistgatan 9 SE-169 70 Solna, Sweden Telephone: +46 8 655 97 00 Fax: +46 8 655 97 33 Email: [email protected] Internet: www.sipri.org The New Nuclear Forensics Analysis of Nuclear Materials for Security Purposes EDITED BY VITALY FEDCHENKO OXFORD UNIVERSITY PRESS 2015 1 Great Clarendon Street, Oxford OX2 6DP, United Kingdom Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries © SIPRI 2015 The moral rights of the authors have been asserted All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of SIPRI, or as expressly permitted by law, or under terms agreed with the appropriate reprographics rights organizations.
    [Show full text]