DOCSLIB.ORG

1 ECE 305 Homework SOLUTIONS: Week 8 Mark Lundstrom Purdue

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1 ECE 305 Homework SOLUTIONS: Week 8 Mark Lundstrom Purdue ECE 305 Spring 2015 ECE 305 Homework SOLUTIONS: Week 8 Mark Lundstrom Purdue University 1) The sketch below shows the carrier concentrations in a PN junction at room temperature. Answer the following questions. 1a) Is the diode forward or reverse biased? Explain your answer. Solution: Forward biased because there are excess electrons on the P-side and excess holes on the N-side. 1b) What is the acceptor concentration on the P-side? 16 -3 Solution: N A = 10 cm 1c) What is the donor concentration on the N-side? 14 -3 Solution: N D = 10 cm 1d) What is the intrinsic carrier concentration? Solution: n p n2 0 0 = i On the P-side: n p = 1016 ×107 = 1023 n = 1023 = 3.16 ×1011 cm-3 0 0 i On the N-side: n p = 1014 ×109 = 1023 n = 1023 = 3.16 ×1011 cm-3 0 0 i n = 3.16 ×1011 cm-3 i ECE-305 1 Spring 2015 ECE 305 Spring 2015 HW8 solutions (continued): 1e) Do low level injection conditions apply? Solution: YES. On the P-side: Δn −x = 1010 << p = 1016 ( p ) 0 On the N-side: Δp x = 1012 << n = 1014 ( n ) 0 1f) What bias (in volts) is applied to the diode? Solution: According the the law of the junction: 2 n qV k T qV k T Δn −x = i e A B = n e A B ( p ) N p0 A 10 k T Δn −xp ⎛ 10 ⎞ V = B ln ( ) = 0.026ln = 0.18 V A q n ⎜ 107 ⎟ p0 ⎝ ⎠ V = 0.18 V A 1g) Which is longer: the electron diffusion length on the P-side of the junction or the hole diffusion length on the N-side of the junction. Solution: The electron diffusion length on the P-side. (The diffusion length is the distance it takes for the minority carrier concentration to return to its value in the bulk. Question: What would the figure look like for a reverse biased diode? 2) This problem concerns the energy band diagram shown below for a diode under bias. ECE-305 2 Spring 2015 ECE 305 Spring 2015 HW8 solutions (continued): 2a) Is the diode forward or reverse biased? Solution: Forward biased because F > F . n p 2b) What is the value of the applied bias? Solution: qV = F − F A n p V = +0.5 V A 2c) What is the bandgap of the semiconductor? Solution: Reading from the graph: E − E = 1.25 eV C V 2d) What is the built-in potential of the junction. Solution: From the plot: V = V −V = 0.25 V j bi A Since: V 0.5 V A = + V = V +V = 0.75 V V = 0.75 V bi j A bi 3) A silicon diode is asymmetrically doped at N 1019 cm-3 and N 1016 cm-3. (Note D = A = that at N 1019 the semiconductor is on the edge of degeneracy, but we can assume D = that non-degenerate carrier statistics are close enough for this problem.) Answer the following questions assuming room temperature. Assume that the minority electron and hole lifetimes are τ = τ = 10−6 s. The lengths of the N and P regions are n p L = 500 µm and L >> x ,x . p n ECE-305 3 Spring 2015 ECE 305 Spring 2015 HW8 Solutions (continued): 3a) Find the zero-bias depletion region capacitance per cm2 of diode area. Solution: The junction capacitance per unit area is: K ε C = s 0 J W V ( A ) The depletion region width for a one-sided junction is: 1/2 ⎡2KSε0 ⎤ W (VA = 0) = ⎢ Vbi ⎥ ⎣ qN A ⎦ The built-in potential is k T ⎛ N N ⎞ V B ln D A bi = ⎜ 2 ⎟ q ⎝ ni ⎠ Putting in numbers, we find: k T ⎛ N N ⎞ ⎛ 10191016 ⎞ V B ln D A 0.026ln 0.90 V bi = ⎜ 2 ⎟ = ⎜ 20 ⎟ = q ⎝ ni ⎠ ⎝ 10 ⎠ 1/2 1/2 ⎡2K ε ⎤ ⎡2 ×11.8 × 8.854 ×10−14 ⎤ W V 0 S 0 V 0.90 3.43 10−5 cm ( A = ) = ⎢ bi ⎥ = ⎢ −19 16 × ⎥ = × ⎣ qN A ⎦ ⎣ 1.6 ×10 ×10 ⎦ (Note that we used in F/cm and N in cm-3 so that the result would come out ε0 A in cm not in meters.) K ε 11.8 × 8.845×10−14 C = s 0 = = 3.05×10−8 F/cm2 J 0 W V = 0 2.8 ×10−5 ( A ) C = 3.05×10−8 F/cm2 J 0 3b) Find the depletion capacitance at V 5 V (reverse biased). A = − Solution: W V 0 Ksε0 Ksε0 ( A = ) Vbi CJ 0 CJ = = × = CJ 0 = W V W V = 0 W V Vbi −VA 1−V V ( A ) ( A ) ( A ) A bi −8 3.05×10 −8 2 CJ = = 1.19 ×10 F/cm < CJ 0 1+ 5 0.9 C V = −5 V = 1.19 ×10−8 F/cm2 J ( A ) Reverse bias decreases the junction capacitance. ECE-305 4 Spring 2015 ECE 305 Spring 2015 HW8 Solutions (continued): 3c) Find the depletion capacitance at V 0.5 V (forward biased). A = + Solution: −8 CJ 0 3.73×10 −8 2 CJ = = = 5.6 ×10 F/cm > CJ 0 1−V V 1− 0.5 0.9 A bi C V = −5 V = 4.58 ×10−8 F/cm2 Forward bias increases the junction J ( A ) capacitance. 4) A silicon diode is asymmetrically doped at N 1019 cm-3 and N 1016 cm-3. (Note D = A = that at N 1019 the semiconductor is on the edge of degeneracy, but we can assume D = that non-degenerate carrier statistics are close enough for this problem.) Assume that the minority electron and hole lifetimes are τ = τ = 10−6 s. The lengths of the N and n p P regions are L = 500 µm and L >> x ,x . p n 4a) Estimate the applied forward bias at which the P-region enters high-level injection. Solution: High injection will occur first on the lightly doped side, the P-side. The maximum excess electron concentration occurs at the beginning of the P-side. From the law of the junction: 2 n qV k T Δn 0 = i e A B −1 ( ) N ( ) A Low level injection means: Δn 0 << N ( ) A Let’s estimate the voltage needed to go into high-level injection, this way 2 n qV k T Δn 0 = i e HL B −1 = N (*) ( ) N ( ) A A A more conservative estimate would be Δn 0 = 0.1N , but (*) is close enough ( ) A for us now. Using (*) as the criteria: 2 k T ⎛ N ⎞ k T ⎛ N ⎞ V = B ln A = 2 B ln A HL q ⎜ n ⎟ q ⎜ n ⎟ ⎝ i ⎠ ⎝ i ⎠ ⎛ 1016 ⎞ V = 2 × 0.026 × ln = 0.781 V HL ⎜ 1010 ⎟ ⎝ ⎠ V = 0.718 V HL ECE-305 5 Spring 2015 ECE 305 Spring 2015 HW8 Solutions (continued): 4b) Compute the current density at the onset of high-injection. Solution: The current density is given by: qV k T J = J e A B −1 0 ( ) From HW8, problem 1): J = 9.1×10−12 A/cm2 0 qV k T J = J e A B −1 = 9.1×10−12 e0.718/0.026 −1 = 9 A/cm2 0 ( ) ( ) J = 9 A/cm2 5) A silicon diode is asymmetrically doped at N 1019 cm-3 and N 1016 cm-3. (Note D = A = that at N 1019 the semiconductor is on the edge of degeneracy, but we can assume D = that non-degenerate carrier statistics are close enough for this problem.) Answer the following questions assuming room temperature. Assume that the minority electron and hole lifetimes are τ = τ = 10−6 s. The lengths of the N and P regions are n p L = 500 µm and L >> x ,x . What is the reverse breakdown voltage of this diode? p n Assume a critical field for breakdown of E = 3×105 V/cm. cr Solution: 1/2 2Vbi 2(Vbi +VR ) ⎡2qN A (Vbi +VR )⎤ E (0) = = 1/2 = W ⎢ K ε ⎥ ⎡2KSε0 ⎤ ⎣ S 0 ⎦ ⎢ (Vbi +VR )⎥ ⎣ qN A ⎦ 1/2 ⎡2qN A (Vbi +VR )⎤ E cr =E (0) = ⎢ K ε ⎥ ⎣ S 0 ⎦ K ε E 2 V = S 0 cr −V BR 2qN bi A k T ⎛ N N ⎞ ⎛ 10191016 ⎞ V B ln D A 0.026ln 0.90 bi = ⎜ 2 ⎟ = ⎜ 20 ⎟ = q ⎝ ni ⎠ ⎝ 10 ⎠ 2 2 11.8 8.854 10−14 3 105 KSε0E cr × × × ( × ) VBR = − 0.90 = −19 16 − 0.90 = 29.4 − 0.90 = 28.5 V 2qN A 2 ×1.6 ×10 ×10 VBR = 28.5 V This assumes a planar junction. If there is junction curvature at the edge of the diode, the breakdown voltage will be lower. ECE-305 6 Spring 2015 .
Load more

Recommended publications
  • PN Junction Is the Most Fundamental Semiconductor Device
    Fundamentals of Microelectronics CH1 Why Microelectronics? CH2 Basic Physics of Semiconductors CH3 Diode Circuits CH4 Physics of Bipolar Transistors CH5 Bipolar Amplifiers CH6 Physics of MOS Transistors CH7 CMOS Amplifiers CH8 Operational Amplifier As A Black Box 1 Chapter 2 Basic Physics of Semiconductors 2.1 Semiconductor materials and their properties 2.2 PN-junction diodes 2.3 Reverse Breakdown 2 Semiconductor Physics Semiconductor devices serve as heart of microelectronics. PN junction is the most fundamental semiconductor device. CH2 Basic Physics of Semiconductors 3 Charge Carriers in Semiconductor To understand PN junction’s IV characteristics, it is important to understand charge carriers’ behavior in solids, how to modify carrier densities, and different mechanisms of charge flow. CH2 Basic Physics of Semiconductors 4 Periodic Table This abridged table contains elements with three to five valence electrons, with Si being the most important. CH2 Basic Physics of Semiconductors 5 Silicon Si has four valence electrons. Therefore, it can form covalent bonds with four of its neighbors. When temperature goes up, electrons in the covalent bond can become free. CH2 Basic Physics of Semiconductors 6 Electron-Hole Pair Interaction With free electrons breaking off covalent bonds, holes are generated. Holes can be filled by absorbing other free electrons, so effectively there is a flow of charge carriers. CH2 Basic Physics of Semiconductors 7 Free Electron Density at a Given Temperature E n 5.21015T 3/ 2 exp g electrons/ cm3 i 2kT 0 10 3 ni (T 300 K) 1.0810 electrons/ cm 0 15 3 ni (T 600 K) 1.5410 electrons/ cm Eg, or bandgap energy determines how much effort is needed to break off an electron from its covalent bond.
    [Show full text]
  • Junction Field Effect Transistor (JFET)
    Junction Field Effect Transistor (JFET) The single channel junction field-effect transistor (JFET) is probably the simplest transistor available. As shown in the schematics below (Figure 6.13 in your text) for the n-channel JFET (left) and the p-channel JFET (right), these devices are simply an area of doped silicon with two diffusions of the opposite doping. Please be aware that the schematics presented are for illustrative purposes only and are simplified versions of the actual device. Note that the material that serves as the foundation of the device defines the channel type. Like the BJT, the JFET is a three terminal device. Although there are physically two gate diffusions, they are tied together and act as a single gate terminal. The other two contacts, the drain and source, are placed at either end of the channel region. The JFET is a symmetric device (the source and drain may be interchanged), however it is useful in circuit design to designate the terminals as shown in the circuit symbols above. The operation of the JFET is based on controlling the bias on the pn junction between gate and channel (note that a single pn junction is discussed since the two gate contacts are tied together in parallel – what happens at one gate-channel pn junction is happening on the other). If a voltage is applied between the drain and source, current will flow (the conventional direction for current flow is from the terminal designated to be the gate to that which is designated as the source). The device is therefore in a normally on state.
    [Show full text]
  • The P-N Junction (The Diode)
    Lecture 18 The P-N Junction (The Diode). Today: 1. Joining p- and n-doped semiconductors. 2. Depletion and built-in voltage. 3. Current-voltage characteristics of the p-n junction. Questions you should be able to answer by the end of today’s lecture: 1. What happens when we join p-type and n-type semiconductors? 2. What is the width of the depletion region? How does it relate to the dopant concentration? 3. What is built-in voltage? How to calculate it based on dopant concentrations? How to calculate it based on Fermi levels of semiconductors forming the junction? 4. What happens when we apply voltage to the p-n junction? What is forward and reverse bias? 5. What is the current-voltage characteristic for the p-n junction diode? Why is it different from a resistor? 1 From previous lecture we remember: What happens when you join p-doped and n-doped pieces of semiconductor together? When materials are put in contact the carriers flow under driving force of diffusion until chemical potential on both sides equilibrates, which would mean that the position of the Fermi level must be the same in both p and n sides. This results in band bending: - + - + + - - Holes diffuse + Electrons diffuse The electrons will diffuse into p-type material where they will recombine with holes (fill in holes). And holes will diffuse into the n-type materials where they will recombine with electrons. 2 This means that eventually in vicinity of the junction all free carriers will be depleted leaving stripped ions behind, which would produce an electric field across the junction: The electric field results from the deviation from charge neutrality in the vicinity of the junction.
    [Show full text]
  • Lecture 16 the Pn Junction Diode (III)
    Lecture 16 The pn Junction Diode (III) Outline • Small-signal equivalent circuit model • Carrier charge storage –Diffusion capacitance Reading Assignment: Howe and Sodini; Chapter 6, Sections 6.4 - 6.5 6.012 Spring 2007 Lecture 16 1 I-V Characteristics Diode Current equation: ⎡ V ⎤ I = I ⎢ e(Vth )−1⎥ o ⎢ ⎥ ⎣ ⎦ I lg |I| 0.43 q kT =60 mV/dec @ 300K Io 0 0 V 0 V Io linear scale semilogarithmic scale 6.012 Spring 2007 Lecture 16 2 2. Small-signal equivalent circuit model Examine effect of small signal adding to forward bias: ⎡ ⎛ qV()+v ⎞ ⎤ ⎛ qV()+v ⎞ ⎜ ⎟ ⎜ ⎟ ⎢ ⎝ kT ⎠ ⎥ ⎝ kT ⎠ I + i = Io ⎢ e −1⎥ ≈ Ioe ⎢ ⎥ ⎣ ⎦ If v small enough, linearize exponential characteristics: ⎡ qV qv ⎤ ⎡ qV ⎤ ()kT (kT ) (kT )⎛ qv ⎞ I + i ≈ Io ⎢e e ⎥ ≈ Io ⎢e ⎜ 1 + ⎟ ⎥ ⎣⎢ ⎦⎥ ⎣⎢ ⎝ kT⎠ ⎦⎥ qV qV qv = I e()kT + I e(kT ) o o kT Then: qI i = • v kT From a small signal point of view. Diode behaves as conductance of value: qI g = d kT 6.012 Spring 2007 Lecture 16 3 Small-signal equivalent circuit model gd gd depends on bias. In forward bias: qI g = d kT gd is linear in diode current. 6.012 Spring 2007 Lecture 16 4 Capacitance associated with depletion region: ρ(x) + qNd p-side − n-side (a) xp x = xn vD VD − qNa = − QJ qNaxp ρ(x) + qNd p-side −x −x n-side (b) p p x xn xn = + > > vD VD vd VD-- − qNa x < x |q | < |Q | p p, J J = − qJ qNaxp = ∆ ∆ρ = ρ − ρ qj qNa xp (x) (x) (x) + qNd X p-side d n-side (c) x n xn − − xp xp x q = q − Q > j j j 0 − qN = −qN x − −qN a − = − ∆ a p ( axp) qj qNd xn = − qNa (xp xp) ∆ = qNa xp Depletion or junction capacitance: dqJ C j = C j (VD ) = dvD VD qεsNa Nd C j = A 2()Na + Nd ()φB −VD 6.012 Spring 2007 Lecture 16 5 Small-signal equivalent circuit model gd Cj can rewrite as: qεsNa Nd φB C j = A • 2()Na + Nd φB ()φB −VD C or, C = jo j V 1− D φB φ Under Forward Bias assume V ≈ B D 2 C j = 2C jo Cjo ≡ zero-voltage junction capacitance 6.012 Spring 2007 Lecture 16 6 3.
    [Show full text]
  • Photodetectors
    Photodetectors • Convert light signals to a voltage or current. • The absorption of photons creates electron hole pairs. • Electrons in the CB and holes in the VB. • A p + n type junction describes a heavily doped p-type material(acceptors) that is much greater than a lightly doped n-type material (donor) that it is embedded into. • Illumination window with an annular electrode for photon passage. • Anti-reflection coating ( Si 3 N 4 ) reduces reflections. Vr (a) SiO 2 R Vout Electrode p+ Iph Photodetectors h" > E + g h e– n E + Antireflection Electrode • The side is on the order of less than a coating p W Depletion region micron thick (formed by planar diffusion ! (b) net into n-type epitaxial layer). eNd x • A space charge distribution occurs about the junction within the depletion layer. –eNa E (x) (c) • The depletion region extends x predominantly into the lightly doped n region ( up to 3 microns max) E max (a) A schematic diagram of a reverse biased pn junction photodiode. (b) Net space charge across the diode in the depletion region. Nd and Na are the donor and acceptor concentrations in the p and n sides. (c). The field in the depletion region. © 1999 S.O. Kasap, Optoelectronics (Prentice Hall) Photodetectors Short wavelengths (ex. UV) are absorbed at the surface, and longer wavelengths (IR) will penetrate into the depletion layer. What would be a fundamental criteria for a photodiode with a wide spectral response? Thin p-layer and thick n layer. What does thickness of depletion layer determine (along with reverse bias)? Diode capacitance.
    [Show full text]
  • Chapter 2 Semiconductor Heterostructures
    Semiconductor Optoelectronics (Farhan Rana, Cornell University) Chapter 2 Semiconductor Heterostructures 2.1 Introduction Most interesting semiconductor devices usually have two or more different kinds of semiconductors. In this handout we will consider four different kinds of commonly encountered heterostructures: a) pn heterojunction diode b) nn heterojunctions c) pp heterojunctions d) Quantum wells, quantum wires, and quantum dots 2.2 A pn Heterojunction Diode Consider a junction of a p-doped semiconductor (semiconductor 1) with an n-doped semiconductor (semiconductor 2). The two semiconductors are not necessarily the same, e.g. 1 could be AlGaAs and 2 could be GaAs. We assume that 1 has a wider band gap than 2. The band diagrams of 1 and 2 by themselves are shown below. Vacuum level q1 Ec1 q2 Ec2 Ef2 Eg1 Eg2 Ef1 Ev2 Ev1 2.2.1 Electron Affinity Rule and Band Alignment: How does one figure out the relative alignment of the bands at the junction of two different semiconductors? For example, in the Figure above how do we know whether the conduction band edge of semiconductor 2 should be above or below the conduction band edge of semiconductor 1? The answer can be obtained if one measures all band energies with respect to one value. This value is provided by the vacuum level (shown by the dashed line in the Figure above). The vacuum level is the energy of a free electron (an electron outside the semiconductor) which is at rest with respect to the semiconductor. The electron affinity, denoted by (units: eV), of a semiconductor is the energy required to move an electron from the conduction band bottom to the vacuum level and is a material constant.
    [Show full text]
  • Deep Level Transient Spectroscopy and Uniaxial Stress System
    -.•lu^iiznnajtii ^jx'Hi < ii^iuijgaMWiitwqpnfffjffij^ii^Tip r«iiFi!.:iT.g7:=^^ DEEP LEVEL TRANSIENT SPECTROSCOPY AND UNIAXIAL STRESS SYSTEM by SHILIAN YANG, B.S. A THESIS IN PHYSICS Submitted to the Graduate Faculty of Texas Tech University in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE December, 1990 gmfiaBssrs. PC ^ ACKNOWLEDGEMENTS I would like to acknowledge the Department of Physics, Texas Tech University, for its academic and financial support of my graduate studies for the last three years. I also would like to thank my advisor. Dr. C. D. Lamp, for his patience and support which have greatly helped me finish this project and Dr. S. Gangopadhyay for her helpful ideas. I also very much appreciate the help of Mr. B. D. Jones as well as the people in the physics shop, without them finishing this project would have been impossible. 11 Kv '-*_-•<-•«-'•*•-Tff finiiiiwiuitiMiLLMttajefty&^^^> TABLE OF CONTENTS ACKNOWLEDGEMENTS ii ABSTRACT iv LIST OF FIGURES v CHAPTER I. INTRODUCTION 1 II. DLTS THEORY 3 2.1 Trap Concentrations And Emission Rates 5 2.2 Junction Transient Capacitance 10 2.3 Defect Energy, Capture Cross Section And Concentration 15 2.4 Digital DLTS System 19 III. UNIAXIAL STRESS 28 3.1 Uniaxial Stress Theory 29 3.2 Uniaxial Stress Apparatus 35 IV. THE EXPERIMENT 43 4.1 EL2 In GaAs 43 4.2 Sample Preparation 45 4.3 Experimental Results And Discussion 47 REFERENCES 58 111 ABSTRACT Deep level transient spectroscopy (DLTS) combined with uniaxial stress will not only determine the energy level of a defect center in semiconductor but also tell its symmetry, which is very important for identifying the structure of a defect center.
    [Show full text]
  • Depletion Capacitance
    Linearly Graded Junction zThe Poisson equation for the case is 2 d Ψ − q −W W 2 = ax ≤x ≤ dx ε s 2 2 zWhere a is impurity gradient and W is depletion width area. ulfiqar Ali32 Z1EEE 1 Figure 4-11. Linearly graded junction in thermal equilibrium. (a) Impurity distribution. (b) Electric-field distribution. (c) Potential distribution with distance. (d) Energy band diagram. EEE132 Zulfiqar Ali 2 Linearly graded junction zBuilt in Voltage for Linearly Graded Junction ⎡ W W ⎤ (a )(a ) kT ⎢ 2 2 ⎥ 2kT ⎡aW ⎤ Vbi = ln⎢ 2 ⎥ = ln⎢ ⎥ q q 2n ⎢ ni ⎥ ⎣ i ⎦ ⎣⎢ ⎦⎥ EEE132 Zulfiqar Ali 3 Depletion Capacitance The depletion layer capacitance per unit area is defined dQ Cj = dV Where dQ is incremental charge per unit area as for an incremental charge per unit voltage. EEE132 Zulfiqar Ali 4 Figure 4.13. (a) p-n junction with an arbitrary impurity profile under reverse bias. (b) Change in space charge distribution due to change in applied bias. (c) Corresponding change in electric-field distribution. EEE132 Zulfiqar Ali 5 Depletion Capacitance zWhenever voltage dv is applied. The charge filed distribution will expand. Figure shows the region bounded by dashed line. zThis increment bring increase in electric field by an amount of dQ dε = ε s EEE132 Zulfiqar Ali 6 Capacitance-Voltage Characteristic zSeparation between two plates represents the depletion width. Refer to the figure 13. zFor forward bias large current can flow across the junction corresponding to large number of mobile carrier. zThe incremental change of these mobile carriers with respect to the biasing voltage contributes an additional term called diffusion capacitance.
    [Show full text]
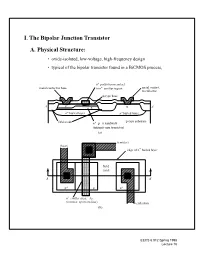
  • I. the Bipolar Junction Transistor A. Physical Structure
    I. The Bipolar Junction Transistor A. Physical Structure: • oxide-isolated, low-voltage, high-frequency design • typical of the bipolar transistor found in a BiCMOS process, n+ polysilicon contact metal contact to base to n+ emitter region metal contact to collector p-type base + + A p n n A' n+ buried layer n+ buried layer p-type substrate field oxide n+ - p - n sandwich (intrinsic npn transistor) (a) (emitter) (base) edge of n+ buried layer field oxide A A' + p p n+ + n emitter area, AE (intrinsic npn transistor) (collector) (b) EECS 6.012 Spring 1998 Lecture 16 B. Circuit Symbol and Terminal Characteristics • Two devices that have complementary characterisitics npn transistor and the pnp transistor • The direction of the diode arrow indicates device type npn pnp C E IC IE + + + VEB B V B − V + CE EC − IB VBE − IB − − −I −I E E C C (a) (b) Normal operation: Normal operation: I positive V positive C CE –IC positive VEC positive I positive V = 0.7 B BE –IB positive VEB = 0.7 -IE positive IE positive EECS 6.012 Spring 1998 Lecture 16 C. npn BJT Collector Characteristics • Similar test circuit as for n-channel MOSFET ... except IB is controlled instead of VBE = IC IC(IB, VCE) + V − CE IB (a) I C = µ (µA) IB 2.5 A 300 = µ IB 2 A 250 200 I = 1.5 µA (saturation) B 150 = µ (forward active) IB 1 A 100 = IB 500 nA 50 I = 0 (cutoff) −3 −2 −1 B 1 2 3 4 5 6 VCE (V) = µ −4 IB 1 A (reverse active) −8 = µ IB 2 A (b) EECS 6.012 Spring 1998 Lecture 16 D.
    [Show full text]
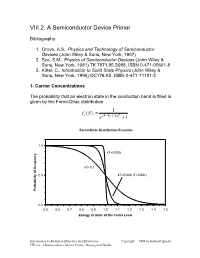
  • VIII.2. a Semiconductor Device Primer
    VIII.2. A Semiconductor Device Primer Bibliography: 1. Grove, A.S., Physics and Technology of Semiconductor Devices (John Wiley & Sons, New York, 1967) 2. Sze, S.M., Physics of Semiconductor Devices (John Wiley & Sons, New York, 1981) TK 7871.85.S988, ISBN 0-471-05661-8 3. Kittel, C., Introduction to Solid State Physics (John Wiley & Sons, New York, 1996) QC176.K5, ISBN 0-471-11181-3 1. Carrier Concentrations The probability that an electron state in the conduction band is filled is given by the Fermi-Dirac distribution = 1 fe (E) − e(E EF )/kBT +1 Fermi-Dirac Distribution Function 1.0 kT=0.005 kT=0.1 0.5 kT=0.026 (T=300K) Probability of Ocupancy 0.0 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 Energy in Units of the Fermi Level Introduction to Radiation Detectors and Electronics Copyright 1998 by Helmuth Spieler VIII.2.a. A Semiconductor Device Primer, Doping and Diodes The density of atoms in a Si or Ge crystal is about 4.1022 atoms/cm3. Since the minimum carrier density of interest in practical devices is of order 1010 to 1011 cm-3, very small ocupancy probabilities are quite important. Fermi-Dirac Distribution Function 1.0E+00 1.0E-02 1.0E-04 1.0E-06 kT=0.035 eV (T=400K) 1.0E-08 kT=0.026 eV (T=300K) 1.0E-10 1.0E-12 Probability of Occupancy 1.0E-14 1.0E-16 1.0E-18 0.8 0.9 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 Energy in Units of Fermi Level In silicon the band gap is 1.12 eV.
    [Show full text]
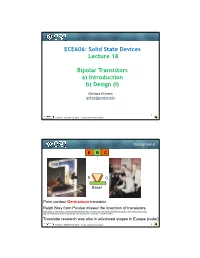
  • ECE606: Solid State Devices Lecture 18 Bipolar Transistors A
    ECE606: Solid State Devices Lecture 18 Bipolar Transistors a) Introduction b) Design (I) Gerhard Klimeck [email protected] 1 Klimeck – ECE606 Fall 2012 – notes adopted from Alam Background E B C E C Base! Point contact Germanium transistor Ralph Bray from Purdue missed the invention of transistors. http://www.electronicsweekly.com/blogs/david-manners-semiconductor-blog/2009/02/how-purdue-university-nearly-i.html http://www.physics.purdue.edu/about_us/history/semi_conductor_research.shtml Transistor research was also in advanced stages in Europe (radar). Klimeck – ECE606 Fall 2012 – notes adopted from Alam 2 Shockley’s Bipolar Transistors … n+ emitter n+ Double p base n-collector Diffused BJT n+ n+ p n n+ emitter base collector Klimeck – ECE606 Fall 2012 – notes adopted from Alam Modern Bipolar Junction Transistors (BJTs) Base Emitter Collector N+ N- P+ N+ N SiGe intrinsic base P- Dielectric trench Why do we need all these design? Transistor speed increases as the electron's travel distance is reduced SiGe Layer Klimeck – ECE606 Fall 2012 – notes adopted from Alam 4 Symbols and Convention E Symbols Poly emitter N+ NPN PNP Collector B P Low-doped base Collector Base Base N Collector doping optimization Emitter Emitter C IC+I B+I E=0 (DC) VEB +V BC +V CE =0 Klimeck – ECE606 Fall 2012 – notes adopted from Alam 5 Outline 1) Equilibrium and forward band-diagram 2) Currents in bipolar junction transistors 3) Eber’s Moll model 4) Intermediate Summary 5) Current gain in BJTs 6) Considerations for base doping 7) Considerations for collector doping
    [Show full text]
  • Junction Field Effect Transistors (JFET)
    1 Lecture-11 Junction Field Effect Transistors (JFET) Introduction: The field effect transistor, or simply the FET is a three-terminal semiconductor device used extensively in digital and analog circuits. There are two types of such devices, the MOSFET and JFET, acronyms for the metal oxide semiconductor and junction field-effect transistors, respectively. In this lecture, we study about the characteristics and small signal model of the JFET. FET differs from the bipolar junction transistor in the following important characteristics: 1. Its operation depends upon the flow of majority carriers only. It is therefore, a unipolar (one type of carrier) device. 2. It is simpler to fabricate and occupies less space in integrated form. 3. It exhibits a high input resistance, typically many megaohms. 4. It is less noisy than bipolar device The Ideal Voltage Controlled Current Source: The operating characteristics are similar that of the voltage controlled current source device. In this section the characteristics of the ideal-voltage controlled current source is presented. The Fig.1(a) shows a ideal-voltage controlled current source, is a three-terminal device, in which the control voltage v1 is applied to the terminal 1-3 and the current source gmv1 acts at terminals 2-3. The parameter gm is called the transconductance or mutual conductance, relates the strength of the source to the control voltage. The output characteristics of the voltage controlled current source are shown in the Fig.1(b), on which a load line corresponding to RL and V22 is drawn. The load line represents the KVL equation for the output loop (containing terminals 2-3) in the circuit shown in Fig1(c).
    [Show full text]