Resampling-Based Tests of Functional Categories in Gene Expression Studies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

RNA Expression Patterns in Serum Microvesicles from Patients With
Noerholm et al. BMC Cancer 2012, 12:22 http://www.biomedcentral.com/1471-2407/12/22 RESEARCHARTICLE Open Access RNA expression patterns in serum microvesicles from patients with glioblastoma multiforme and controls Mikkel Noerholm1,2*, Leonora Balaj1, Tobias Limperg1,3, Afshin Salehi1,4, Lin Dan Zhu1, Fred H Hochberg1, Xandra O Breakefield1, Bob S Carter1,4 and Johan Skog1,2 Abstract Background: RNA from exosomes and other microvesicles contain transcripts of tumour origin. In this study we sought to identify biomarkers of glioblastoma multiforme in microvesicle RNA from serum of affected patients. Methods: Microvesicle RNA from serum from patients with de-novo primary glioblastoma multiforme (N = 9) and normal controls (N = 7) were analyzed by microarray analysis. Samples were collected according to protocols approved by the Institutional Review Board. Differential expressions were validated by qRT-PCR in a separate set of samples (N = 10 in both groups). Results: Expression profiles of microvesicle RNA correctly separated individuals in two groups by unsupervised clustering. The most significant differences pertained to down-regulated genes (121 genes > 2-fold down) in the glioblastoma multiforme patient microvesicle RNA, validated by qRT-PCR on several genes. Overall, yields of microvesicle RNA from patients was higher than from normal controls, but the additional RNA was primarily of size < 500 nt. Gene ontology of the down-regulated genes indicated these are coding for ribosomal proteins and genes related to ribosome production. Conclusions: Serum microvesicle RNA from patients with glioblastoma multiforme has significantly down- regulated levels of RNAs coding for ribosome production, compared to normal healthy controls, but a large overabundance of RNA of unknown origin with size < 500 nt. -

BMC Genomics Biomed Central
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Springer - Publisher Connector BMC Genomics BioMed Central Research article Open Access Dual activation of pathways regulated by steroid receptors and peptide growth factors in primary prostate cancer revealed by Factor Analysis of microarray data Juan Jose Lozano1,2,5, Marta Soler3, Raquel Bermudo3, David Abia1, Pedro L Fernandez4, Timothy M Thomson*3 and Angel R Ortiz*1,2 Address: 1Bioinformatics Unit, Centro de Biología Molecular "Severo Ochoa" (CSIC-UAM), Universidad Autónoma de Madrid, Cantoblanco, 28049 Madrid, Spain, 2Department of Physiology and Biophysics, Mount Sinai School of Medicine, One Gustave Levy Pl., New York, NY 10029, USA, 3Instituto de Biología Molecular, Consejo Superior de Investigaciones Científicas, c. Jordi Girona 18–26, 08034 Barcelona, Spain, 4Departament de Anatomía Patològica, Hospital Clínic, and Institut de Investigacions Biomèdiques August Pi i Sunyer, c. Villarroel 170, 08036 Barcelona, Spain and 5Center for Genome Regulation, Barcelona (Spain) Email: Juan Jose Lozano - [email protected]; Marta Soler - [email protected]; Raquel Bermudo - [email protected]; David Abia - [email protected]; Pedro L Fernandez - [email protected]; Timothy M Thomson* - [email protected]; Angel R Ortiz* - [email protected] * Corresponding authors Published: 17 August 2005 Received: 17 January 2005 Accepted: 17 August 2005 BMC Genomics 2005, 6:109 doi:10.1186/1471-2164-6-109 This article is available from: http://www.biomedcentral.com/1471-2164/6/109 © 2005 Lozano et al; licensee BioMed Central Ltd. This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. -

Aneuploidy: Using Genetic Instability to Preserve a Haploid Genome?
Health Science Campus FINAL APPROVAL OF DISSERTATION Doctor of Philosophy in Biomedical Science (Cancer Biology) Aneuploidy: Using genetic instability to preserve a haploid genome? Submitted by: Ramona Ramdath In partial fulfillment of the requirements for the degree of Doctor of Philosophy in Biomedical Science Examination Committee Signature/Date Major Advisor: David Allison, M.D., Ph.D. Academic James Trempe, Ph.D. Advisory Committee: David Giovanucci, Ph.D. Randall Ruch, Ph.D. Ronald Mellgren, Ph.D. Senior Associate Dean College of Graduate Studies Michael S. Bisesi, Ph.D. Date of Defense: April 10, 2009 Aneuploidy: Using genetic instability to preserve a haploid genome? Ramona Ramdath University of Toledo, Health Science Campus 2009 Dedication I dedicate this dissertation to my grandfather who died of lung cancer two years ago, but who always instilled in us the value and importance of education. And to my mom and sister, both of whom have been pillars of support and stimulating conversations. To my sister, Rehanna, especially- I hope this inspires you to achieve all that you want to in life, academically and otherwise. ii Acknowledgements As we go through these academic journeys, there are so many along the way that make an impact not only on our work, but on our lives as well, and I would like to say a heartfelt thank you to all of those people: My Committee members- Dr. James Trempe, Dr. David Giovanucchi, Dr. Ronald Mellgren and Dr. Randall Ruch for their guidance, suggestions, support and confidence in me. My major advisor- Dr. David Allison, for his constructive criticism and positive reinforcement. -

The Genetics of Bipolar Disorder
Molecular Psychiatry (2008) 13, 742–771 & 2008 Nature Publishing Group All rights reserved 1359-4184/08 $30.00 www.nature.com/mp FEATURE REVIEW The genetics of bipolar disorder: genome ‘hot regions,’ genes, new potential candidates and future directions A Serretti and L Mandelli Institute of Psychiatry, University of Bologna, Bologna, Italy Bipolar disorder (BP) is a complex disorder caused by a number of liability genes interacting with the environment. In recent years, a large number of linkage and association studies have been conducted producing an extremely large number of findings often not replicated or partially replicated. Further, results from linkage and association studies are not always easily comparable. Unfortunately, at present a comprehensive coverage of available evidence is still lacking. In the present paper, we summarized results obtained from both linkage and association studies in BP. Further, we indicated new potential interesting genes, located in genome ‘hot regions’ for BP and being expressed in the brain. We reviewed published studies on the subject till December 2007. We precisely localized regions where positive linkage has been found, by the NCBI Map viewer (http://www.ncbi.nlm.nih.gov/mapview/); further, we identified genes located in interesting areas and expressed in the brain, by the Entrez gene, Unigene databases (http://www.ncbi.nlm.nih.gov/entrez/) and Human Protein Reference Database (http://www.hprd.org); these genes could be of interest in future investigations. The review of association studies gave interesting results, as a number of genes seem to be definitively involved in BP, such as SLC6A4, TPH2, DRD4, SLC6A3, DAOA, DTNBP1, NRG1, DISC1 and BDNF. -

Telomerase a Prognostic Marker and Therapeutic Target
Telomerase a prognostic marker and therapeutic target By Dipti S. Thakkar A thesis submitted to the University of Central Lancashire in partial fulfilment of the requirements for the degree of Doctor of Philosophy Month Year submitted: June 2010 1 Declaration I declare that while registered as a candidate for this degree I have not been registered as a candidate for any other award from an academic institution. The work present in this thesis, except where otherwise stated, is based on my own research and has not been submitted previously for any other award in this or any other University. DIPTI THAKKAR Signed 2 Abstract Malignant glioma is the most common and aggressive form of tumours and is usually refractory to therapy. Telomerase and its altered activity, distinguishing cancer cells, is an attractive molecular target in glioma therapeutics. The aim of this thesis was to silence telomerase at the genetic level with a view to highlight the changes caused in the cancer proteome and identify the potential downstream pathways controlled by telomerase in tumour progression and maintenance. A comprehensive proteomic study utilizing 2D-DIGE and MALDI-TOF were used to assess the effect of inhibiting two different regulatory mechanisms of telomerase in glioma. RNAi was used to target hTERT and Hsp90α. Inhibition of telomerase activity resulted in down regulation of various cytoskeletal proteins with correlative evidence of the involvement of telomerase in regulating the expression of vimentin. Vimentin plays an important role in tumour metastasis and is used as an indicator of glioma metastasis. Inhibition of telomerase via sihTERT results in the down regulation of vimentin expression in glioma cell lines in a grade specific manner. -

Supplemental Table 1
Supplemental Data Supplemental Table 1. Genes differentially regulated by Ad-KLF2 vs. Ad-GFP infected EC. Three independent genome-wide transcriptional profiling experiments were performed, and significantly regulated genes were identified. Color-coding scheme: Up, p < 1e-15 Up, 1e-15 < p < 5e-10 Up, 5e-10 < p < 5e-5 Up, 5e-5 < p <.05 Down, p < 1e-15 As determined by Zpool Down, 1e-15 < p < 5e-10 Down, 5e-10 < p < 5e-5 Down, 5e-5 < p <.05 p<.05 as determined by Iterative Standard Deviation Algorithm as described in Supplemental Methods Ratio RefSeq Number Gene Name 1,058.52 KRT13 - keratin 13 565.72 NM_007117.1 TRH - thyrotropin-releasing hormone 244.04 NM_001878.2 CRABP2 - cellular retinoic acid binding protein 2 118.90 NM_013279.1 C11orf9 - chromosome 11 open reading frame 9 109.68 NM_000517.3 HBA2;HBA1 - hemoglobin, alpha 2;hemoglobin, alpha 1 102.04 NM_001823.3 CKB - creatine kinase, brain 96.23 LYNX1 95.53 NM_002514.2 NOV - nephroblastoma overexpressed gene 75.82 CeleraFN113625 FLJ45224;PTGDS - FLJ45224 protein;prostaglandin D2 synthase 21kDa 74.73 NM_000954.5 (brain) 68.53 NM_205545.1 UNQ430 - RGTR430 66.89 NM_005980.2 S100P - S100 calcium binding protein P 64.39 NM_153370.1 PI16 - protease inhibitor 16 58.24 NM_031918.1 KLF16 - Kruppel-like factor 16 46.45 NM_024409.1 NPPC - natriuretic peptide precursor C 45.48 NM_032470.2 TNXB - tenascin XB 34.92 NM_001264.2 CDSN - corneodesmosin 33.86 NM_017671.3 C20orf42 - chromosome 20 open reading frame 42 33.76 NM_024829.3 FLJ22662 - hypothetical protein FLJ22662 32.10 NM_003283.3 TNNT1 - troponin T1, skeletal, slow LOC388888 (LOC388888), mRNA according to UniGene - potential 31.45 AK095686.1 CONFLICT - LOC388888 (na) according to LocusLink. -
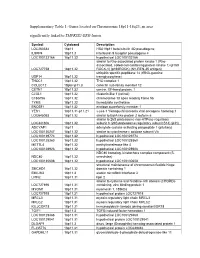
Supplementary Table 1: Genes Located on Chromosome 18P11-18Q23, an Area Significantly Linked to TMPRSS2-ERG Fusion
Supplementary Table 1: Genes located on Chromosome 18p11-18q23, an area significantly linked to TMPRSS2-ERG fusion Symbol Cytoband Description LOC260334 18p11 HSA18p11 beta-tubulin 4Q pseudogene IL9RP4 18p11.3 interleukin 9 receptor pseudogene 4 LOC100132166 18p11.32 hypothetical LOC100132166 similar to Rho-associated protein kinase 1 (Rho- associated, coiled-coil-containing protein kinase 1) (p160 LOC727758 18p11.32 ROCK-1) (p160ROCK) (NY-REN-35 antigen) ubiquitin specific peptidase 14 (tRNA-guanine USP14 18p11.32 transglycosylase) THOC1 18p11.32 THO complex 1 COLEC12 18pter-p11.3 collectin sub-family member 12 CETN1 18p11.32 centrin, EF-hand protein, 1 CLUL1 18p11.32 clusterin-like 1 (retinal) C18orf56 18p11.32 chromosome 18 open reading frame 56 TYMS 18p11.32 thymidylate synthetase ENOSF1 18p11.32 enolase superfamily member 1 YES1 18p11.31-p11.21 v-yes-1 Yamaguchi sarcoma viral oncogene homolog 1 LOC645053 18p11.32 similar to BolA-like protein 2 isoform a similar to 26S proteasome non-ATPase regulatory LOC441806 18p11.32 subunit 8 (26S proteasome regulatory subunit S14) (p31) ADCYAP1 18p11 adenylate cyclase activating polypeptide 1 (pituitary) LOC100130247 18p11.32 similar to cytochrome c oxidase subunit VIc LOC100129774 18p11.32 hypothetical LOC100129774 LOC100128360 18p11.32 hypothetical LOC100128360 METTL4 18p11.32 methyltransferase like 4 LOC100128926 18p11.32 hypothetical LOC100128926 NDC80 homolog, kinetochore complex component (S. NDC80 18p11.32 cerevisiae) LOC100130608 18p11.32 hypothetical LOC100130608 structural maintenance -

MYL12A (1-171, His-Tag) Human Protein – AR39103PU-N | Origene
OriGene Technologies, Inc. 9620 Medical Center Drive, Ste 200 Rockville, MD 20850, US Phone: +1-888-267-4436 [email protected] EU: [email protected] CN: [email protected] Product datasheet for AR39103PU-N MYL12A (1-171, His-tag) Human Protein Product data: Product Type: Recombinant Proteins Description: MYL12A (1-171, His-tag) human recombinant protein, 0.1 mg Species: Human Expression Host: E. coli Tag: His-tag Predicted MW: 22.4 kDa Concentration: lot specific Purity: >90% Buffer: Presentation State: Purified State: Liquid purified protein Buffer System: 20mM Tris-HCl buffer (pH 8.0) containing 20% glycerol, 1mM DTT Preparation: Liquid purified protein Protein Description: Recombinant human MYL12A protein, fused to His-tag at N-terminus, was expressed in E.coli and purified by using conventional chromatography. Storage: Store undiluted at 2-8°C for up to two weeks or (in aliquots) at -20°C or -70°C for longer. Avoid repeated freezing and thawing. Stability: Shelf life: one year from despatch. RefSeq: NP_001289976 Locus ID: 10627 UniProt ID: P19105 Cytogenetics: 18p11.31 Synonyms: HEL-S-24; MLC-2B; MLCB; MRCL3; MRLC3; MYL2B Summary: This gene encodes a nonsarcomeric myosin regulatory light chain. This protein is activated by phosphorylation and regulates smooth muscle and non-muscle cell contraction. This protein may also be involved in DNA damage repair by sequestering the transcriptional regulator apoptosis-antagonizing transcription factor (AATF)/Che-1 which functions as a repressor of p53-driven apoptosis. Alternate splicing results in multiple transcript variants. A pseudogene of this gene is found on chromosome 8.[provided by RefSeq, Dec 2014] This product is to be used for laboratory only. -

Gene Expression-Based Molecular Diagnostic System for Malignant
Imaging, Diagnosis, Prognosis Gene Expression-Based Molecular Diagnostic System for Malignant Gliomas Is Superior to Histological Diagnosis Mitsuaki Shirahata,1, 2 Kyoko Iwao-Koizumi,2 Sakae Saito,2 Noriko Ueno,2 Masashi Oda,1 Nobuo Hashimoto,1Jun A.Takahashi, 1and Kikuya Kato2 Abstract Purpose: Current morphology-based glioma classification methods do not adequately reflect the complex biology of gliomas, thus limiting their prognostic ability.In this study, we focused on anaplastic oligodendroglioma and glioblastoma, which typically follow distinct clinical courses.Our goal was to construct a clinically useful molecular diagnostic system based on gene expression profiling. Experimental Design: The expression of 3,456 genes in 32 patients, 12 and 20 of whom had prognostically distinct anaplastic oligodendroglioma and glioblastoma, respectively, was measured by PCR array.Next to unsupervised methods, we did supervised analysis using a weighted voting algorithm to construct a diagnostic system discriminating anaplastic oligodendroglioma from glioblastoma.The diagnostic accuracy of this system was evaluated by leave-one-out cross-validation.The clinical utility was tested on a microarray-based data set of 50 malignant gliomas from a previous study. Results: Unsupervised analysis showed divergent global gene expression patterns between the two tumor classes.A supervised binary classification model showed 100% (95% confidence interval, 89.4-100%) diagnostic accuracy by leave-one-out cross-validation using 168 diagnostic genes.Applied to a gene expression data set from a previous study, our model correlated better with outcome than histologic diagnosis, and also displayed 96.6% (28 of 29) consistency with the molecular classification scheme used for these histologically controversial gliomas in the original article.Furthermore, we observed that histologically diagnosed glioblastoma samples that shared anaplastic oligodendroglioma molecular characteristics tended to be associated with longer survival. -

Universitat Aut`Onoma De Barcelona Towards Objective Human Brain
Universitat Aut`onoma de Barcelona Departament de Bioqu´ımica i Biologia Molecular Towards Objective Human Brain Tumours Classification using DNA microarrays Dissertation for the degree of Doctor of Biochemistry and Molecular Biology presented by Xavier Castells Domingo This work was performed at the Department of Biochemistry and Molecular Biology of the Universitat Aut`onoma de Barcelona under the supervision of Dr. Carles Ar´us Caralt´o, Dr. Joaqu´ın Ari˜no Carmona and Dr. Anna Barcel´o Vernet Undersigned by Dr. Carles Ar´us Caralt´o Dr. Joaqu´ın Ari˜no Carmona Dr. Anna Barcel´oVernet Xavier Castells Domingo Cerdanyola del Vall`es, 7 May 2009 En agra¨ıment a totes les persones que van decidir donar un tros de bi`opsia al noste grup. Especialment vull dedicar aquesta tesi a la mem`oriade les persones que han mort durant el transcurs de la meva tesi, i de les quals he tingut el gran honor de poder extreure RNA de les seves bi`opsies. Contents Abbreviations xvii 1 INTRODUCTION1 INTRODUCTION1 1.1 Overview on human brain tumours (HBT) . .3 1.1.1 Incidence and mortality of HBT . .3 1.1.2 Description of HBT . .3 1.1.2.1 Diagnosis of HBT in current clinical practice . .3 1.1.2.2 Overview on HBT classification . .5 1.1.3 World Health Organization (WHO) classification criteria . .5 1.1.3.1 Historical overview . .5 1.1.3.2 Entities, variants and patterns . .6 1.1.3.3 Malignancy grade schemes . .7 1.1.3.4 Differences between classification schemes . .7 1.1.3.5 Survival of patients suffering from HBT . -

Gene Expression Profile of Neuronal Progenitor Cells Derived from Hescs: Activation of Chromosome 11P15.5 and Comparison to Human Dopaminergic Neurons
Thomas Jefferson University Jefferson Digital Commons Farber Institute for Neurosciences Faculty Papers Farber Institute for Neurosciences 1-9-2008 Gene expression profile of neuronal progenitor cells derived from hESCs: activation of chromosome 11p15.5 and comparison to human dopaminergic neurons. William J Freed Cellular Neurobiology Research Branch, Intramural Research Program (IRP), National Institute on Drug Abuse, National Institutes of Health (NIH), Department of Health and Human Services (DHHS) Jia Chen Cellular Neurobiology Research Branch, Intramural Research Program (IRP), National Institute on Drug Abuse, National Institutes of Health (NIH), Department of Health and Human Services (DHHS) Cristina M Bäckman CellularFollow this Neur andobiology additional Resear worksch Br at:anch, https:/ Intr/jdc.jeffamuralerson.edu/farberneursofp Research Program (IRP), National Institute on Drug Abuse, National Institutes of Health (NIH), Department of Health and Human Services (DHHS) Part of the Medical Cell Biology Commons, and the Neurosciences Commons LetCatherine us Mknow Schwar tzhow access to this document benefits ouy Laboratory of Neurosciences, Intramural Research Program (IRP), National Institute on Aging, National Institutes of Health (NIH), Department of Health and Human Services (DHHS) Recommended Citation FTrandiseed, William Vazin J; Chen, Jia; Bäckman, Cristina M; Schwartz, Catherine M; Vazin, Tandis; Cai, Cellular Neurobiology Research Branch, Intramural Research Program (IRP), National Institute on Drug Jingli; Spivak, Charles E; Lupica, Carl R; Rao, Mahendra S; and Zeng, Xianmin, "Gene expression Abuse, National Institutes of Health (NIH), Department of Health and Human Services (DHHS) profile of neuronal progenitor cells derived from hESCs: activation of chromosome 11p15.5 and comparison to human dopaminergic neurons." (2008). Farber Institute for Neurosciences FSeeaculty next P pageapers. -

MRCL3 (MYL12A) (NM 001303049) Human Untagged Clone Product Data
OriGene Technologies, Inc. 9620 Medical Center Drive, Ste 200 Rockville, MD 20850, US Phone: +1-888-267-4436 [email protected] EU: [email protected] CN: [email protected] Product datasheet for SC334193 MRCL3 (MYL12A) (NM_001303049) Human Untagged Clone Product data: Product Type: Expression Plasmids Product Name: MRCL3 (MYL12A) (NM_001303049) Human Untagged Clone Tag: Tag Free Symbol: MYL12A Synonyms: HEL-S-24; MLC-2B; MLCB; MRCL3; MRLC3; MYL2B Vector: pCMV6-Entry (PS100001) E. coli Selection: Kanamycin (25 ug/mL) Cell Selection: Neomycin Fully Sequenced ORF: >NCBI ORF sequence for NM_001303049, the custom clone sequence may differ by one or more nucleotides ATGGACTTAACCACCACCATGTCGAGCAAAAGAACAAAGACCAAGACCAAGAAGCGCCCTCAGCGTGCAA CATCCAATGTGTTTGCTATGTTTGACCAGTCACAGATTCAGGAGTTCAAAGAGGCCTTCAACATGATTGA TCAGAACAGAGATGGTTTCATCGACAAGGAAGATTTGCATGATATGCTTGCTTCATTGGGGAAGAATCCA ACTGATGAGTATCTAGATGCCATGATGAATGAGGCTCCAGGCCCCATCAATTTCACCATGTTCCTCACCA TGTTTGGTGAGAAGTTAAATGGCACAGATCCTGAAGATGTCATCAGAAATGCCTTTGCTTGCTTTGATGA AGAAGCAACTGGCACCATACAGGAAGATTACTTGAGAGAGCTGCTGACAACCATGGGGGATCGGTTTACA GATGAGGAAGTGGATGAGCTGTACAGAGAAGCACCTATTGATAAAAAGGGGAATTTCAATTACATCGAGT TCACACGCATCCTGAAACATGGAGCCAAAGACAAAGATGACTGA Restriction Sites: SgfI-MluI ACCN: NM_001303049 OTI Disclaimer: Our molecular clone sequence data has been matched to the reference identifier above as a point of reference. Note that the complete sequence of our molecular clones may differ from the sequence published for this corresponding reference, e.g., by representing an alternative