DOCSLIB.ORG

Establishing Normative Templates.Pdf (8.392Mb)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Establishing Normative Templates.Pdf (8.392Mb) '7Ò7 6 t ¡. 7Zç 10242680 €vt+ Mc00 'lUC o illilt I r lil]llil il]il ilil I ilt ililt E STABLI SHING NORMATIVE TEMPLATE S IN PERFORMANCE ANALYSIS OF BADMINTON 0t >. CYNCOED ¡.ii,l. ' TEPHEN EV ÈC)R u5Ê il\ ']BRARY ONLV A project submitted in partial fulfilment of the requirements for the Degree of Master of Science (Coaching Science) School of Graduate and Continuing Education Faculty of Education and Sport University of Wales Institute, Cardiff September 1999 PRIF"TSGOL CYMRU UNTVERSITY OF }VALES THE DEGREE OF MASTER OF SCIENCE Declaration of student in respect to their work I CERTIF"Y that this work has not been previously accepted in substance for any degree, and is not being concurrently submitted in candidature for any other degree. I further certi$r that the whole of this work is the result of my individual effort, except where otherwise stated. All quotations from books and journals have been acknowledged. A list ofreferences is appended. I hereby give consent for my dissertation, if accepted, to be available for photocopying, and for interJibrary loan, and for the title and summary to be made available to outside organisations. Signed: (candidate) Date: sql1 l33 Certificate of supervising tutor in respect of the student's individual work I am SATISFIED that this work is the result of the above-named student's own effort. Signed: Date: 'I am playing all the right shots, but not necessarily in the right order.' Adapted from an Eric Morecambe and Ernie Wise sketch With thanks to Dr. Mike Hughes for his experience and my mother for her support. ll A notation system, designed to record rally-end variables in Badminton, \¡ras shown to be both valid and reliable. Inter and intra reliability ranged from 98.6% (Rally length) to gl.3% (Position). Percentage differences between data from side, and end observations of the same match were not greater than for the intra-reliability data thus different court viewing angles had little effect on notation. Previous literature declared profiles of performance without adequately tackling the problem of quantifuing of the data required in creating a normative template. The badminton notation system was used to examine the cumulative means of selected variables over a series of 1l matches of a player. A template, at match \n¡, was established when these means became stable within set limits of error (LE). T{ests on the variable means in games won, and games lost established the existence of winning and losing templates for winners and effors. Match descriptors (rallies, shots and shots per rally) were independent of match outcome. General values of NtBl established for data types, (10% LE), were 3 matches (descriptive variables), 4 (winners/errors (w/e)), 6 (smash + øe), 7 (position + de). Respective values at 5Yo LE were '7, 5,8 and lO.There was little difference in the values of NtBl when variable means were analysed by game than by match. For the working performance analyst the results provide an estimate of the minimum number of matches to profile an opponent's rally-end play. Whilst the results may be limited to badminton, men's singles and the individual, the methodology of using graphical plots of cumulative means in attempting to establish templates of performance has been served. lll TABLE OF CONTENTS PAGE DECLARATION ACKNOWLEDGEMENTS l1 ABSTRACT LIST OF TABLES vtn LIST OF FIGURES xl CHAPTER ONE INTRODUCTION I 1.1 Notation and badminton I 1.2 The bacþround for the study 1 1.3 The statement of the problems 5 1.4 The hypotheses 6 lv 1.5 The limitations and de-limitations 7 CHAPTER TWO REVIEV/ OF LITERATURE 9 2.1 Reviewing the literature 9 2.2.1 Notational analysis in badminton 9 2.2.2 Defining profiles, templates and models 1l 2.2.3 Creating arally ending template l3 2.2.4 The use of performance indicators 15 2.3.1 Using research to define methodology t7 2.3.2 Definition of sample size 18 2.3.3 Dividing the playing surface t9 2.3.4 Defining actions and outcomes 2t 2.3.7 System validation and reliability 22 2.3.6 Reliability and camera position 24 2.3.7 Statistical analysis 25 2.4 The rationale of the study 27 v CHAPTER THREE METHODOLOGY 29 3.1 Notation system design 29 3.2 The notation database 32 J.J Subject and matches 4l 3.4 Equipment 4l 3.5 System validation 46 3.6 Testing system reliability 46 3.7 Reliability and camera position 48 3.8 Collecting the data 48 3.9 The analysis procedures employed 49 CHAPTER FOUR RESULTS 52 CHAPTERFIVE DISCUSSION 96 5.1.1 Inter-observer reliability 96 5.1.2 Intra-observer reliability 97 5.1.3 Reliability and camera angle 99 5.2 Research design 101 11 5.3 The descriptive summary data 103 5.4 Establishing templates of winning 104 and losing 5.5 Establishing templates of matches 105 and games 5.6 The definition of templates 106 CHAPTER SIX CONCLUSIONS 110 CHAPTER SEVEN REFERENCES 111 CHAPTER EIGI{T APPENDIX lt8 vll LIST OF TABLES TABLE PAGE 31 Abbreviation codes for actions and outcomes 30 3.2 List of matches involving Player A" in order of analysis 42 J.J Match list of wins by Player A 42 3.4 Match list of losses by Player A 42 3.5 The definitions of actions and outcomes 43 3.6 An example of winner/error interpretation and the effect on other variables 47 4.1 Results of intra-observer reliability study 52 4.2 Results of inter-observer reliability study 52 4.3 Results of camera angle reliability study 52 4.4 Intra-observer differences betvieen each set ofvariables 53 4.5 Inter-observer differences between each set ofvariables 54 4.6 Camera view observation differences between each set of variables 55 4.7 Description information of the matches analysed 56 vlll 4.8 Rally frequency information for different match groupings 57 4.9 Shot frequency information for different match groupings 58 4.lO Shot per rally information for different match groupings 58 4.ll The means and percentage error range of rallies by match 59 4.12 The means and percentage error range of shots by match 59 4.13 The means and percentage effor range of shots per rally by match 62 4.14 Shot and rally information for fìrst games 64 4.15 Shot and rally information for first games 65 4.16 The means and limits of error of rallies by game 67 4.17 The means and limits of error of shots by game 69 4. l8 The means and limits of error of shots/rally by game 7t 4.19 Summary of the number of matches to establish variable templates 73 4.20 Summary of the number of matches to establish variable templates 73 4.21 Frequency of winners by match outcome for Player A 74 4.22 Frequency of errors by match outcome for Player A 74 4.23 Frequency of winners by match outcome for Opponent 75 4.24 Frequency of errors by match outcome for Opponent 75 lx 4.25 Frequency of winners by game outcome for Player A 76 4.26 Frequency of errors by game outcome for Player A 76 4.27 Frequency of winners by game outcome for Opponent 76 4.28 Frequency of errors by game outcome for Opponent 76 4.29 Summary of the number of games to establish awinner and an error profile when Player Awins 86 4.30 Summary of the number of games to establish a winner and an error profile when Player A loses 86 4.31 Overall summary ofN(E) for all variable measured at each limit of error 95 x LIST OF FIGURES FIGURE PAGE 3.1 The division of the badminton court into position cells 3l 3.2 The list of tables in the Rally-end database 34 3.3 A list of queries in the Access Rally-end database 35 3.4 Furtherqueries in the Access Rally-end database 36 3.5 The design view of the rally table 37 3.6 An example of the data input table 38 3.7 The design view of a database query 39 3.8 An example of a database query output 40 4.1 Mean number of rallies by match 60 4.2 Mean number of shots by match 6l 4.3 Mean number of shots per rally by match 63 4.4 Mean number of rallies by game 68 4.5 Mean number of shots by game 70 4.6 Mean number of shots per rally by game 72 4.7 Player A's winners when Player Awins the game 78 4.8 Player A's errors when Player Awins the game 79 xl 4.9 Opponent's winners when Player A wins the game 80 4.10 Opponent's effors when Player Awins the game 81 4.ll Player A's winners when Player A loses the game 82 4.12 Player A's errors when Player A loses the game 83 4.13 Opponent's winners when Player A loses the game 84 4.14 Opponent's errors when Player A loses the game 85 4.15 Player A's smash winners by match 88 4.16 Player A's smash errors by match 89 4.17 Opponent's smash winners by match 90 4.18 Opponent's smash errors by match 9t 4.19 Player A's winners from position 3 per match 9l 4.20 Player A's errors from position 3 per match 92 4.21 Opponent's winners from position 3 per match 93 4.22 Opponent's errors from position 3 per match 94 xll CHAPTERI INTRODUCTION 1.1 Notation and badminton Notation has been utilised throughout history to describe and define movement although its use to facilitate improvements in sport perfonnance is a recent development.
Load more

Recommended publications
  • History of Badminton
    Facts and Records History of Badminton In 1873, the Duke of Beaufort held a lawn party at his country house in the village of Badminton, Gloucestershire. A game of Poona was played on that day and became popular among British society’s elite. The new party sport became known as “the Badminton game”. In 1877, the Bath Badminton Club was formed and developed the first official set of rules. The Badminton Association was formed at a meeting in Southsea on 13th September 1893. It was the first National Association in the world and framed the rules for the Association and for the game. The popularity of the sport increased rapidly with 300 clubs being introduced by the 1920’s. Rising to 9,000 shortly after World War Π. The International Badminton Federation (IBF) was formed in 1934 with nine founding members: England, Ireland, Scotland, Wales, Denmark, Holland, Canada, New Zealand and France and as a consequence the Badminton Association became the Badminton Association of England. From nine founding members, the IBF, now called the Badminton World Federation (BWF), has over 160 member countries. The future of Badminton looks bright. Badminton was officially granted Olympic status in the 1992 Barcelona Games. Indonesia was the dominant force in that first Olympic tournament, winning two golds, a silver and a bronze; the country’s first Olympic medals in its history. More than 1.1 billion people watched the 1992 Olympic Badminton competition on television. Eight years later, and more than a century after introducing Badminton to the world, Britain claimed their first medal in the Olympics when Simon Archer and Jo Goode achieved Mixed Doubles Bronze in Sydney.
    [Show full text]
  • Den Indflydelsesløse Landstræner Spillerforeningens Svar Til Bjørn Danielsen
    Danmark blev overhalet indenom af Indonesien Der kan kun gættes om årsagen til, at Indonesien skal arrangere næste VM på Danmarks bekostning A f H.C. Møller marks sag. Med stor imøde­ er i Asien, og de pågældende kommenhed havde ambassa­ personer var store nok til at Et vel forberedt oplæg godt dør Arne Belling inviteret give Miss Lu den undskyld­ præsenteret af Steen Fladberg IBF’s bestyrelse til frokost­ ning, som nogle mente, hun var ikke nok til at skaffe Dansk møde i ambassaden. Det var i havde krav på. Jens Peter Nierhoff og Mi­ Badminton Forbund arrange­ øvrigt anden gang, at danske le­ chael Kjeldsen ydede en flot mentet af de individuelle ver­ dere og flere af spillerne var i præstation ved VM. Bronze i densmesterskaber i 1989. Dan­ ambassaden, idet alle danske­ Europa udsultes double. mark blev slået i opløbet af In­ re, der var beskæftigede med IBF’s præsident, Ian Palmer, BADMINTON er DBF’s offi­ donesien, der i sit tilbud også badminton i Beijing inden VM var en af dem, der var mest cielle organ, men meninger havde et tre-dages ophold på var ambassadør Bellings gæster overrasket over afstemningens der kommer til udtryk i bla­ Bali med ledsager til de med­ ved et middagsselskab. resultat, og hans spontane re­ det, behøver ikke nødvendig­ lemmer af IBF’s bestyrelse, der Men selv om det indonesiske aktion var at anbefale Frede vis at give udtryk for forbun­ skulle træffe afgørelsen. bestyrelsesmedlem Utus Kur- Kruse at søge VM-arrange- dets mening. — Jeg havde ikke fantasi til at niadi sukkende beklagede sig mentet i 1991.
    [Show full text]
  • Facts and Records
    Badminton England Facts and Records Index (cltr + click to jump to a particular section): 1. History of Badminton 2. Olympic Games 3. World Championships 4. Sudirman Cup 5. Thomas Cup 6. Uber Cup 7. Commonwealth Games 8. European Individual Championships 9. European Mixed Championships 10. England International Caps 11. All England Open Badminton Championships 12. England’s Record in International Matches 13. The Stuart Wyatt Trophy 14. International Open Tournaments 15. International Challenge Tournaments 16. English National Championships 17. The All England Seniors’ Open Championships 18. English National Junior Championships 19. Inter-County Championships 20. National Leisure Centre Championships 21. Masters County Challenge 22. Masters County Championships 23. English Recipients for Honours for Services to Badminton 24. Recipients of Awards made by Badminton Association of England Badminton England Facts & Records: Page 1 of 86 As at May 2021 Please contact [email protected] to suggest any amendments. Badminton England Facts and Records 25. English recipients of Awards made by the Badminton World Federation 1. The History of Badminton: Badminton House and Estate lies in the heart of the Gloucestershire countryside and is the private home of the 12th Duke and Duchess of Beaufort and the Somerset family. The House is not normally open to the general public, it dates from the 17th century and is set in a beautiful deer park which hosts the world-famous Badminton Horse Trials. The Great Hall at Badminton House is famous for an incident on a rainy day in 1863 when the game of badminton was said to have been invented by friends of the 8th Duke of Beaufort.
    [Show full text]
  • The Welsh Badminton Union National Championships
    WALES THE WELSH BADMINTON UNION Contact: Badminton Wales Tel: +02920 334 938 Sport Wales National Centre Mobile: Sophia Gardens Fax: Cardiff, WALES E-mail: [email protected] CF11 9SW Web: www.badminton.wales Founded: January, 1928 President: David Davies E.B.U.: April, 1968 Sportadministrator Players: 1.527 Sportscoordinator: Clubs: 95 clubs (79 senior clubs and Secretary: Kelly Aston 16 junior clubs) Periodical Badminton Wales NATIONAL CHAMPIONSHIPS Men´s Singles Ladies´ Singles 1961 G.E.Rowlands J.Warwick 1962 G.E.Rowlands Angela Davies 1963 M.Anis Angela Davies 1964 Peter Seaman Angela Davies 1965 G.E.Rowlands Angela Davies 1966 G.E.Rowlands Angela Dickson 1967 Peter Seaman Angela Dickson 1968 G.S.R.Tan Angela Dickson 1969 Howard R.Jennings Angela Dickson 1970 Howard R.Jennings Angela Dickson 1971 Howard R.Jennings Angela Dickson 1972 Howard R.Jennings Angela Dickson 1 of 39 1973 No Competition No Competition 1974 Howard R.Jennings Angela Dickson 1975 Howard R.Jennings Angela Dickson 1976 S.Gully Angela Dickson 1977 Howard H.Jennings Sue Brimble 1978 Yim C.Lim Angela Dickson 1979 Yim C.Lim Angela Dickson 1980 Philip Sutton Sian Williams 1981 Philip Sutton Sian Williams 1982 Philip Sutton Angela Nelson 1983 Philip Sutton Sian Williams 1984 Philip Sutton Angela Nelson 1985 Philip Sutton Sian Williams 1986 Christopher Rees Lesley Roberts 1987 Christopher Rees Rachel McIntosh 1988 Christopher Rees Gail Davies 1989 Christopher Rees Gail Davies 1990 Andrew Spencer Rachele Edwards 1991 Andrew Spencer Rachele Edwards 1992 Mark
    [Show full text]
  • Elitetrænerudd. 1991-1994
    ----------------------- BADMINTON------------------------ Værn om DBF’s største sponsor A f Bjørn Danielsen Det vrimler med VM-tal. I 565 mer for, at dette VM kan blive en pelvis kan det nævnes, at en gen- dage har 120 personer været op­ succes, tilsammen er DBF’s største nemsnits-købstads-kommune bru­ taget af VM -forberedelser. Under sponsor. ger godt fire millioner kroner på arrangementet fra 30. april til 12. Beløbet 11.980.000 kroner er 700 medlemmer i en ungdoms­ maj vil yderligere knap 1000 per­ meget lavt sat - det er snarere to­ klub, mens idrættens 7.000 med­ soner være beskæftiget som tre gange større. lemmer må dele seks miil. kr. med chauffører, guider, kontrollører, Tankevækkende, at de frivillige de uniformerede korps m.m. i den liniedommere, dommere og me­ ledere både til dette VM, men også samme by. get, meget mere. rundt om i DBFs godt 600 klubber Det er mit ønske, at dette VM Hvis vi til forberedelse af VM si­ ofrer utallige timer på frivilligt ar­ bliver en succes for DBF, delta­ ger, at hver person har brugt en bejde, på trods af den behandling gerne og de mange frivillige ledere time dagligt får vi: Folketinget og kommunerne byder - det er aldrig så galt at yde en fri­ 120 personer i 565 dage å 1 dem. villig indsats, når resultatet bliver time = 67.800 timer. Hvis vi sæt­ Den nye folkeoplysningslov har påskønnet. ter et gennemsnit på fire timers ar­ for alvor vist, at der er tale om en Det er også mit håb, at det frivil­ bejde dagligt under VM får vi: besparelseslov.
    [Show full text]
  • Aristo Bolde
    Nu kan du igen lave dit drømmesmash ARISTO BOLDE Elitens naturlige valg -d e t eneste alternativ er... MATADOR som med fordel anvendes i mange turneringer ISSN 0005-3791 På vej mod bedre spiller-klassificering Eneste helt sikre løsning er dog en »licens«-ordning DBFs turneringsudvalg har i sendt ud I foråret, og der er ryd­ Den perfekte løsning ville vel starten af denne måned kunnet det ud i de værste fejl. siger for­ være en licens-nr. ordning? præsentere spiller-klassificerin­ manden for turneringsudvalget, gen for sæson 1983-84, og den Bjørn Holst-Christensen. -Ja . Det har jeg talt for for flere kan uden tvivl få prædikatet Vi har fået begrænset antallet år siden uden at det er lykkedes »bedste klassificering i adskilli­ af »dobbeltgængere« m.v. at slå igennem med det. Men det Morten Frost fører feltet an. ge år«. Med årets klassificering er erklärt, at det ville være den ene­ Det er unge spillere fra Nr. Dermed ikke blot tænkt på DBF gået ind i EDB-alderen med ste rigtige og fornuftige ordning, Broby, der løber med. Morten selve inddelingen af de enkelte hensyn til styringen af klassifi­ at alle skulle registreres som tur­ tilbragte en weekend I det spillere i mester-, A-, B-, C- eller cerings-listerne. På dette punkt nerings-spillere, før de kunne fynske for at træne med D-række, men på udtyndingen af har klubberne ikke hjulpet så stille op i åbne turneringer, siger landsbyklubbens unge, in­ fejl i listen. godt, som man gerne havde set Bjørn Holst-Christensen. den han 13. august tog på »Badminton« har igennem fra TU’s side.
    [Show full text]
  • England Tog Guldet I EM for Hold
    Elitens naturlige valg -d e t eneste alternativ er... MATADOR som med fordel anvendes i mange turneringer Dominion Sports Industri tlf. 02-24 24 24 - lokal 12 anviser nærmeste forhandler All England Kina-trium fer i VM -forproven Rollerne byttet fra i fjor. Luan Jin vinder, All England - vinderen Zhang Ailing (t.h.) og Jianqiu. Morten Frost tabende finalist. Danskere til tops Jesper Helledie og Steen Fladberg jubler. Har vundet såvel hollandske som svenske Claus Thomsen- åbne mesterskaber. ungdoms-europamester. ISSN 0005-3791, ’Badminton’ er officielt organ for Dansk Badminton Forbund. Udgiver: Svend Erik Ja­ cobsen, Vestergade 23, 3200 Helsinge, for Dansk Badminton Forbund. Redaktion: Sv. E. Jacobsen (ansvarshavende), tlf. 02-29 69 55, H. C. Møller, Jørgen Hjort (Foto), Preben Søborg (Foto). Annoncer: Sv. E. Jacobsen, Vestergade 23, 3200 Helsinge, tlf. 02-29 69 55. Abonnement på »Badminton« koster 75,- kr. og bestilles hos udgiveren eller via DBF’s kontor. Tryk: Buwi Tryk-3200 Helsinge-TIf. (02) 29 60 10. Bladets artikler med undtagelse af ’Officielle meddelelser’ må citeres uden tilladelse, når det fremgår, at det stammer fra ’Badminton’. Meninger, der kommer til udtryk i bladet, behøver Ikke nød­ vendigvis at give udtryk for forbundets mening. 3 All England Nogle siger fiasko andre mener succes Steen Skovgaard og Jens Peter Nierhoff nåede semifinalen i herredouble i All England. På et tidspunkt, da fodbold­ var med i endnu en positiv over­ landskampe mod Sverige var i raskelse, da han sammen med stand til at hidse den halve na­ Jens Peter Nierhoff spillede sig tion op, sagde Svend Pri en­ frem til semifinalen i herredoub­ gang: - Hvis Danmark taber 1-2 le, efter at det useedede par i til svenskerne, har fodbold­ tur og orden havde gjort det af landsholdet vundet en halv sejr, med de 6-seedede koreanere men hvis jeg bliver slået i fina­ Joo Bong Park/Eun Ku Lee, fina­ len i All England, er det en fias­ listerne fra sidste All England ko for dansk badminton.
    [Show full text]
  • Aus Dem Inhalt
    F 20433 E Badminton Rundschau Amtliches Organ des 30. Jahrgang Badminton-Landesverbandes 5. April 1987 Nord rhei n-Westfa len e. V. Nr. 4 Aus dem Inhalt Der Leser hat das Wort 2 Berichte Westdeutsche u. Deutsche Juniorenmeisterschaft 3 All-England Open 4-5 Turnierausschreibungen 6 Schulsport 8 Amtliche Nachrichten Klasseneinteilung für die Saison 1987/88 10-16 Schüler- u. Jugendturniere für die Saison 1987/88 16-20 Das Urteil 22 Trainer-Ratschläge 23 Morten Frost (Dänemark) Sieger bei den ALL-England Open. Foto: Ingo Kurth Der Leser hat das Wort Vorstand BLV NRW e.V. Präsident: an allen wichtigen Punkten (Schulen, Banken, Dr. Hans-Richard Lange Öffentlichkeitsarbeit Geschäfte) verteilen. Bei entscheidenden Spie­ Ubierstraße 57b, 5300 Bonn 2 len Werbung in den Nachbarvereinen machen. Telefon (0228) 351917 Grundsätzlich fragt sich wohl jeder Badminton­ 4) Bewährt hat sich bei uns eine Stadtmei­ verein, wie er eine größere Öffentlichkeit errei­ sterschaft für Nicht-Vereinsspieler, eventu­ Vizepräsidenten: chen kann, um 1) mehr Zuschauer zu den Spie­ ell mit Preisen. Diese Stadtmeisterschaft groß Horst Boldt len bzw. Turnieren anzuziehen und/oder 2) ankündigen mit dem ausdrücklichen Verweis Mellinghofer Str. 181, 4200 Oberhausen 1 mehr Mitglieder für die Vereine zu werben. auf die Hobbyklasse. Dadurch können gerade Telefon (02 08) 86 29 97 Patentlösungen gibt es keine. Einige Vor­ oft talentierte Jugendliche und Schüler heraus­ schläge, die zum einen mit wenig Kosten ver­ gefiltert werden. · Siegfried Maywald bunden sind und zum anderen bei uns in 5) Für die Zuschauer bei den Spielen sind Zähl• Rose nweg 5, 5300 Bonn 3 Lüdinghausen recht erfolgreich waren, möchte tafeln das entscheidende Mittel überhaupt die Telefon (02 28) 47 4716 ich an dieser Stelle vorstellen.
    [Show full text]
  • Evropska Prvenstva (1968-2010)
    EVROPSKA PRVENSTVA (1968-2010) 1. EUROPEAN CHAMPIONSHIPS, 1968 April 19-21, Bochum, F.R. Germany Men’s Singles 1. Sture Johnsson (SWE) 2. Wolfgang Bochow (FRG) 3. Elo Hansen (DEN) Jorgen Mortensen (DEN) Ladies’ Singles 1. Irmgard Latz (FRG) 2. Marie Luisa Wackerow (FRG) 3. Eva Twedberg (SWE) Angela Bairstow (ENG) Men’s Doubles 1. David Eddy & Roger Powell (ENG) 2. Tony Jordan & Roger Mills (ENG) 3. Robert McCoig & Mac Henderson (SCO) Franz Beinvogl & Willi Braun (FRG) Ladies’ Doubles 1. Margaret Boxall & Susan Whetnall (ENG) 2. Angela Bairstow & Gillian Perrin (ENG) 3. Agnes Geene & Joke van Beusekom (NED) Anne Flindt & Bente Soerensen (DEN) Mixed Doubles 1. Tony Jordan & Susan Whetnall (ENG) 2. Roger Mills & Gillian Perrin (ENG) 3. Wolfgang Bochow & Irmgard Latz (FRG) Klaus Kagaard & Anne Flindt (DEN) 2. EUROPEAN CHAMPIONSHIPS, 1970 April 17-19, Port Talbot, Wales Men’s Singles 1. Sture Johnsson (SWE) 2. Elo Hansen (DEN) 3. Paul Whetnall (ENG) Wolfgang Bochow (FRG) Ladies’ Singles 1. Eva Twedberg (SWE) 2. Imre R. Nielsen (DEN) 3. Lisbeth von Barnekow(DEN) Margaret Boxal (ENG) Men’s Doubles 1. Elo Hansen & Per Walsoe (DEN) 2. Erland Kops & Henning Borch (DEN) 3. Siegfried Betz & Roland Maywald (FRG) David Eddy & Roger Powell (ENG) Ladies’ Doubles 1. Margaret Boxal & Susan Whetnall (ENG) 2. Irmgard Latz & MarieLuisa Wackerow (FRG) 3. Karin Jorgensen & Anne Berglund (DEN) Gillian Perrin & Margaret Beck (ENG) Mixed Doubles 1. David Eddy & Susan Whetnall (ENG) 2. Derek Talbot & Gillian Perrin (ENG) 3. Per Walsoe & Anne Berglund (DEN) Wolfgang Bochow & Irmgard Latz (FRG) 3. EUROPEAN CHAMPIONSHIPS, 1972 April 14-16, Karlskrona, Sweden Men’s Singles 1 Wolfgang Bochow (FRG) 2.
    [Show full text]
  • Euroopa Meistrivõistlused Sulgpallis. Meeste Üksikmäng
    EUROOPA MEISTRIVÕISTLUSED SULGPALLIS. MEESTE ÜKSIKMÄNG Jrk Aasta & võistluspaik Riik Kuld Riik Hõbe Riik Pronksid 1968 SWE Sture Johnsson FRG Wolfgang Bochow DEN Elo Hansen DEN Jørgen Mortensen 1 Bochum (Frg) F: 17:14, 11:15, 15:5 1970 SWE Sture Johnsson DEN Elo Hansen ENG Paul Whetnall FRG Wolfgang Bochow 2 Port Talbot (Wal) F: 1972 FRG Wolfgang Bochow (1) DEN Klaus Kaagaard ENG Ray Stevens DEN Flemming Delfs 3 Karlskrona (Swe) F: 1974 SWE Sture Johnsson (3) SWE Thomas Kihlström DEN Flemming Delfs ENG Derek Talbot 4 Viin (Aut) F: 1976 DEN Flemming Delfs DEN Elo Hansen FRG Wolfgang Bochow ENG Paul Whetnall 5 Dublin (Irl) F: 1978 DEN Flemming Delfs SWE Thomas Kihlström SWE Sture Johnsson ENG Ray Stevens 6 Preston (Eng) F: 1980 DEN Flemming Delfs (3) DEN Morten Frost DEN Svend Pri ENG Ray Stevens 7 Groningen F: 1982 DEN Jens Peter Nierhoff (1) ENG Ray Stevens DEN Claus Andersen ENG Nick Yates 8 Böblingen (Frg) F: 1984 DEN Morten Frost DEN Jens Peter Nierhoff ENG Steve Baddeley SWE Göran Karlsson 9 Preston (Eng) F: 1986 DEN Morten Frost (2) DEN Ib Frederiksen DEN Michael Kjeldsen DEN Torben Carlsen 10 Uppsala (Swe) F: 1988 ENG Darren Hall (1) DEN Morten Frost URS Andrei Antropov DEN Michael Kjeldsen 11 Kristiansand (Nor) F: 1990 ENG Steve Baddeley (1) ENG Darren Hall ENG Steve Butler DEN Poul-Erik Høyer Larsen 12 Moskva (Urs) F: 1992 DEN Poul-Erik Høyer Larsen DEN Thomas Stuer Lauridsen DEN Peter Espersen ENG Anders Nielsen 13 Glasgow (Sco) F: 15:10, 15:10 1994 DEN Poul-Erik Høyer Larsen SWE Tomas Johansson SWE Jens Olsson ENG Anders Nielsen
    [Show full text]
  • Euroopa Meistrivõistlused Sulgpallis. Meeste Üksikmäng
    EUROOPA MEISTRIVÕISTLUSED SULGPALLIS. MEESTE ÜKSIKMÄNG Jrk Aasta & võistluspaik Riik Kuld Riik Hõbe Riik Pronksid 1968 SWE Sture Johnsson FRG Wolfgang Bochow DEN Elo Hansen DEN Jørgen Mortensen 1 Bochum (Frg) F: 17:14, 11:15, 15:5 1970 SWE Sture Johnsson DEN Elo Hansen ENG Paul Whetnall FRG Wolfgang Bochow 2 Port Talbot (Wal) F: 1972 FRG Wolfgang Bochow (1) DEN Klaus Kaagaard ENG Ray Stevens DEN Flemming Delfs 3 Karlskrona (Swe) F: 1974 SWE Sture Johnsson (3) SWE Thomas Kihlström DEN Flemming Delfs ENG Derek Talbot 4 Viin (Aut) F: 1976 DEN Flemming Delfs DEN Elo Hansen FRG Wolfgang Bochow ENG Paul Whetnall 5 Dublin (Irl) F: 1978 DEN Flemming Delfs SWE Thomas Kihlström SWE Sture Johnsson ENG Ray Stevens 6 Preston (Eng) F: 1980 DEN Flemming Delfs (3) DEN Morten Frost DEN Svend Pri ENG Ray Stevens 7 Groningen F: 1982 DEN Jens Peter Nierhoff (1) ENG Ray Stevens DEN Claus Andersen ENG Nick Yates 8 Böblingen (Frg) F: 1984 DEN Morten Frost DEN Jens Peter Nierhoff ENG Steve Baddeley SWE Göran Karlsson 9 Preston (Eng) F: 1986 DEN Morten Frost (2) DEN Ib Frederiksen DEN Michael Kjeldsen DEN Torben Carlsen 10 Uppsala (Swe) F: 1988 ENG Darren Hall (1) DEN Morten Frost URS Andrei Antropov DEN Michael Kjeldsen 11 Kristiansand (Nor) F: 1990 ENG Steve Baddeley (1) ENG Darren Hall ENG Steve Butler DEN Poul-Erik Høyer Larsen 12 Moskva (Urs) F: 1992 DEN Poul-Erik Høyer Larsen DEN Thomas Stuer Lauridsen DEN Peter Espersen ENG Anders Nielsen 13 Glasgow (Sco) F: 15:10, 15:10 1994 DEN Poul-Erik Høyer Larsen SWE Tomas Johansson SWE Jens Olsson ENG Anders Nielsen
    [Show full text]
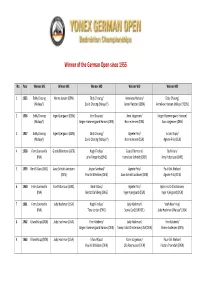
  • Winner of the German Open Since 1955
    Winner of the German Open since 1955 No. Year Winner MS Winner WS Winner MD Winner WD Winner MX 1. 1955 Eddy Choong Hanne Jensen (DEN) Eddy Choong/ Anneliese Hansen/ Eddy Choong/ (Malaya*) David Choong (Malaya*) Grete Fledsted (DEN) Anneliese Hansen (Malaya*/DEN) 2. 1956 Eddy Choong Inger Kjærgaard (DEN) Jörn Skaarup/ Anni Jörgensen/ Jörgen Hammergaard Hansen/ (Malaya*) Jörgen Hammergaard Hansen (DEN) Hanne Jensen (DEN) Anni Jörgensen (DEN) 3. 1957 Eddy Choong Inger Kjærgaard (DEN) Eddy Choong/ Agnete Friis/ Erland Kops/ (Malaya*) David Choong (Malaya*) Hanne Jensen (DEN) Agnete Friis (DEN) 4. 1958 Ferry Sonneville Gisela Ellermann (GER) Hugh Findlay/ Gisela Ellermann/ Bo Nilson/ (INA) John Timperley (ENG) Hannelore Schmidt (GER) Amy Pettersson (SWE) 5. 1959 Bertil Glans (SWE) Aase Schiött-Jacobsen Jesper Sandvad/ Agnete Friis/ Poul-Erik Nielsen/ (DEN) Poul-Erik Nielsen (DEN) Aase Schiött Jacobsen (DEN) Agnete Friis (DEN) 6. 1960 Ferry Sonneville Eva Pettersson (SWE) Bertil Glans/ Agnete Friis/ Björn Holst-Christensen/ (INA) Berndt Dahlberg (SWE) Inger Kjærgaard (DEN) Inger Kjærgaard (DEN) 7. 1961 Ferry Sonneville Judy Hashman (USA) Hugh Findlay/ Judy Hashman/ Yeoh Kean Hua/ (INA) Tony Jordan (ENG) Sonia Cox (USA/NZL) Judy Hashman (Malaya*/USA) 8. 1962 Erland Kops (DEN) Judy Hashman (USA) Finn Kobberö/ Judy Hashman/ Finn Kobberö/ Jörgen Hammergaard Hansen (DEN) Tonny Holst-Christensen (USA/DEN) Hanne Andersen (DEN) 9. 1963 Erland Kops (DEN) Judy Hashman (USA) Erland Kops/ Karin Jörgensen/ Poul-Erik Nielsen/ Poul-Erik Nielsen (DEN) Ulla Rasmussen (DEN) Kirsten Thorndahl (DEN) No. Year Winner MS Winner WS Winner MD Winner WD Winner MX 10. 1964 Erland Kops (DEN) Judy Hashman (USA) Erland Kops/ Angela Bairstow/ Finn Kobberö/ Poul-Erik Nielsen (DEN) Jennifer Pritchard (ENG) Bente Flindt (DEN) 11.
    [Show full text]