Cooling of Anionic Metal Clusters Stored in an Electrostatic Ion Beam Trap
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

P1-Extreme Amplifier by David Sorlien, Revised and Updated by Stephen Keller
Introduction to Tube Amplifier Theory: 10.02.15 Featuring the AX84 P1-eXtreme Amplifier by David Sorlien, revised and updated by Stephen Keller The P1-eX amplifier is a simple three-stage vacuum tube electric guitar amplifier. As outlined in Fig. 1, it consists of two preamp stages driving a power amp stage. Depending on the choice of output tube, this amp is can deliver between 7 and 15 watts into a 4-, 8-, or 16-ohm load. Fig. 1: P1-eX block diagram Placed between the two preamp stages is a preamp volume control. In a similar manner, the bass, middle, and treble tone controls and a master volume control are placed between the preamp and the final power amp stage. The guitar amplifier performs two primary functions: One, it amplifies the small voltages and currents produced by the guitar pickup into a signal powerful enough to drive a speaker. Two, it shapes the frequency response, tonality, and distortion characteristics of the raw guitar signal into a form pleasing to the musician. To better grasp how a guitar amplifier accomplishes these functions, let©s take a walk through the inner workings of the AX84 P1-eXtreme amp (P1-eX). For reference, there is copy of revision 06.03.16 of the schematic provided in Appendix 1 at the end of this document. To fully understand how a guitar amp works, even a simple one like the P1-eX, you must know how to read schematic diagrams, and understand what things like resistors and capacitors are. You also need some knowledge of basic algebra and electronic theory. -

The Beginner's Handbook of Amateur Radio
FM_Laster 9/25/01 12:46 PM Page i THE BEGINNER’S HANDBOOK OF AMATEUR RADIO This page intentionally left blank. FM_Laster 9/25/01 12:46 PM Page iii THE BEGINNER’S HANDBOOK OF AMATEUR RADIO Clay Laster, W5ZPV FOURTH EDITION McGraw-Hill New York San Francisco Washington, D.C. Auckland Bogotá Caracas Lisbon London Madrid Mexico City Milan Montreal New Delhi San Juan Singapore Sydney Tokyo Toronto McGraw-Hill abc Copyright © 2001 by The McGraw-Hill Companies. All rights reserved. Manufactured in the United States of America. Except as per- mitted under the United States Copyright Act of 1976, no part of this publication may be reproduced or distributed in any form or by any means, or stored in a database or retrieval system, without the prior written permission of the publisher. 0-07-139550-4 The material in this eBook also appears in the print version of this title: 0-07-136187-1. All trademarks are trademarks of their respective owners. Rather than put a trademark symbol after every occurrence of a trade- marked name, we use names in an editorial fashion only, and to the benefit of the trademark owner, with no intention of infringe- ment of the trademark. Where such designations appear in this book, they have been printed with initial caps. McGraw-Hill eBooks are available at special quantity discounts to use as premiums and sales promotions, or for use in corporate training programs. For more information, please contact George Hoare, Special Sales, at [email protected] or (212) 904-4069. TERMS OF USE This is a copyrighted work and The McGraw-Hill Companies, Inc. -
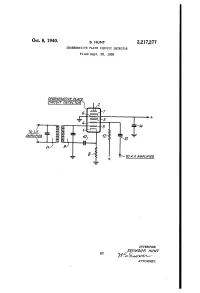
6\ M?L/ K7 Gmwy 4 I ' + /‘4 I- E 7 4-‘1 :"I'yl’‘‘‘‘ ‘N I ‘ 7'0 LP 2: J- = ' '
Oct.’ 8, 1940. s. HUNT £2,217,277 ' ‘ DEGENERATIVE PLATE cmcun: DETECTOR Filed Sept. '28, 19:8 DEGENERAT/VE PLATE __———_C/RCU/T DETECTOR | /2 6\ M?l/ k7 gmwy 4 i ' + /‘4 i- E 7 4-‘1 :"I'Yl’‘‘‘‘ ‘n I ‘ 7'0 LP 2: J- = ' ' a . °~ I ?|__' I ~ 70 A. E AMPLIFIER INVENTOR. Ilse MOUR HUNT BY ATTORNEY. Patented Oct. 8, 1940 2,2l7,277 UNITED STATES F ICE 2,217,277 DEGENERAT'IVE PLATE CIRCUIT DETECTOR Seymour Hunt, Jackson Heights, Long llsland, N. Y., assignor to Radio Corporation of Amer ica, a corporation of Delaware Application September 28, 1938, Serial No. 232,075 6 Claims. (Cl. 256-4237) My present invention relates to detector cir art are fully acquainted with the construction of cuits, and more particularly to degenerative plate superheterodyne receivers, it is not believed nec circuit detectors capable of substantially ampli essary to explain the construction thereof at any fying the audio voltage output thereof. greater length. The output electrode for the 5 One of the main objects of this invention is to detector circuit includes electrode 4. Preferably, provide a detector of the in?nite impedance type this electrode is a wound grid. The latter is con which includes an electronic section having a nected through load resistor 52 to the plus B negative mutual conductance characteristic terminal of any desired direct current source, which functions to amplify the audio output of such as the usual direct current energizing source 10 the detector. of a radio receiver. The coupling condenser l3 Another important object is to provide in a transmits the audio voltage, in ampli?ed form, biased plate circuit detector of the degenerative to the following audio ampli?er for ?nal repro type a negative mutual conductance section duction. -

Electrostatic Design and Characterization of a 200 Kev Photogun and Wien Spin Rotator
Old Dominion University ODU Digital Commons Electrical & Computer Engineering Theses & Dissertations Electrical & Computer Engineering Spring 2021 Electrostatic Design and Characterization of a 200 keV Photogun and Wien Spin Rotator Gabriel G. Palacios Serrano Old Dominion University, [email protected] Follow this and additional works at: https://digitalcommons.odu.edu/ece_etds Part of the Computer Engineering Commons, Electrical and Computer Engineering Commons, and the Physics Commons Recommended Citation Palacios Serrano, Gabriel G.. "Electrostatic Design and Characterization of a 200 keV Photogun and Wien Spin Rotator" (2021). Doctor of Philosophy (PhD), Dissertation, Electrical & Computer Engineering, Old Dominion University, DOI: 10.25777/mf9f-r453 https://digitalcommons.odu.edu/ece_etds/224 This Dissertation is brought to you for free and open access by the Electrical & Computer Engineering at ODU Digital Commons. It has been accepted for inclusion in Electrical & Computer Engineering Theses & Dissertations by an authorized administrator of ODU Digital Commons. For more information, please contact [email protected]. ELECTROSTATIC DESIGN AND CHARACTERIZATION OF A 200 keV PHOTOGUN AND WIEN SPIN ROTATOR by Gabriel G. Palacios Serrano B.S. August 2014, Universidad Autónoma Metropolitana, Mexico M.S. May 2017, Old Dominion University A Dissertation Submitted to the Faculty of Old Dominion University in Partial Fulfillment of the Requirements for the Degree of DOCTOR OF PHILOSOPHY ELECTRICAL AND COMPUTER ENGINEERING OLD DOMINION UNIVERSITY May 2021 Approved by: Helmut Baumgart (Director) Carlos Hernández (Member) Linda Vahala (Member) Mohammad Obeid (Member) Gon Namkoong (Member) ABSTRACT ELECTROSTATIC DESIGN AND CHARACTERIZATION OF A 200 keV PHOTOGUN AND WIEN SPIN ROTATOR Gabriel G. Palacios Serrano Old Dominion University, 2021 Director: Dr. -

Cre|4|L-Feuhis ATTORNEYS Nov
Nov. 28, 1961 M. V. SULLIVAN 3,011,018 HIGHLIGHT APERTURE CORRECTION SYSTEM Filed Sept. 26, 1956 3 Sheets-Sheet 1 NVENTOR MICHAEL V.SULL VAN cre|4|l-feuHIS ATTORNEYS Nov. 28, 1961 M. W. SULLIVAN 3,011,018 HIGHLIGHT APERTURE CORRECTION SYSTEM Filed Sept. 26, 1956 3 Sheets-Sheet 2 aa- ?-s? ? O ???? S I INVENTOR MICHAEL V. SULLIVAN -a?.--77. ? ????? ??? HIS AT TORNEYS Nov. 28, 1961 M. V. SULLIVAN 3,011,018 HIGHLIGHT APERTURE CORRECTION SYSTEM Filed Sept. 26, 1956 3 Sheets-Sheet 3 NVENTOR MiCHAEL V. SULLIVAN Y Cit...!!* His A ?????? la? 3,011,018 United States Patent Office Patented Nov. 28, 1961 3,011,018 FIG. 2 illustrates the waveform of the television pic HIGHLIGHT APERTURE CORRECTION SYSTEM ture signal at various points in the aperture equalization Michael V. Sullivan, Florham Park, N.J., assignor to system shown in FIG. 1; Columbia Broadcasting System, Inc., New York, N.Y., FIG. 3 is a circuit diagram of the input and white a corporation of New York clipper portions of the system shown in FIG. 1; Filed Sept. 26, 1956, Ser. No. 612,221 FIG. 4 is ? circuit diagram of the difference ampli 7 Claims. (Cl. 178-6) fier portion of the system shown in FIG. 1; and FIG. 5 is a circuit diagram of the summing amplifier This invention relates to television, and more particu and output portions of the system shown in FIG.1. larly to a new and improved aperture equalization O Referring first to the block diagram of FIG. 1 and method and means for correcting aperture distortion in the graphic representations of the signal waveform of the highlight regions of the television picture, without FIG.2, a television picture information signal as illus increasing the high frequency noise which is inherent in trated in FIG. -

BY 7% É Arrórney Patent-Ed Nov
Nov. 24, 1942. s. HUNT 2,302,867 COMÈINED MIXER AND INTERMEDIATE FREQUENCY STAGE l Filed Oct. 25, 1941 Q/ T - l INVENToR ’ SEYMOUR BY 7% é ArróRNEY Patent-ed Nov. 24, 1942 2,302,867 . UNITED STATES PATENT OFFICE tratas@r COMBINED MIXER AND INTÉRMEDIATE FREQUENCY STAGE Seymour Hunt, Flushing, N. Y., assîgnor to Radio Corporation of America, a corporation of Dela Ware Application october 25, 1941, serial No. 416,438 8 Claims. (>Cl. 250-20) This invention is concerned with an improve ` accelerate the electron stream and to shield elec ment in radio receivers of the superheterodyne trostatically the signal control grid G4 from volt type and more particularly with a combined first age fluctuations on the oscillator anode-grid G2 detector-oscillator or mixer and intermediate fre and the output anode P. quency stage that may be used with advantage in Cl According to my invention the functions of such receivers. the several electrodes and the connections there In the present state of the art it isknown to tol of the circuit elements are modified somewhat use in superheterodyne circuits a multi-electrode ~ as will now be pointed out more particularly. In type of tube designed to perform simultaneously the circuit of Fig. 1 the grid G1 serves as the the functions of a mixer tube and of an oscillator signal control grid as well as the oscillator grid. tube. According to my present invention the ` Connected between the signal grid G1 and cath same or equivalent multi-electrode tube is made ode 'is the circuit L1-C1 which is tuned to the to perform in addition the function of interme received signal oscillations. -

Lee De Forest Claimet\He Got the Idea for His Triode ''Audion" From
Lee de Forest claimet\he got the idea for his triode h ''audion" from wntching a gas flame bum. John Ambrose Flen#ng thought that story ·~just so much hot air. lreJess telegraphy held excit m WIng promise at the beginning of the twentieth century. Peo ~With Imagination could seethe po.. tentlal thot 'the rematkoble new technology offered forworlct1Nk:le com munfcotion. However, no one could hove predicted the impact that the soon-to-be-developed "osdllotlon volve" ond "oudlon" Wireless-telegra phy detector& wauid have on elec tronics technology. Backpouncl. Shortly before 1900, · Guglielmo Morconl had formed his own company to develop wireless telegraphy technology. He demon strated that wireless set-ups on ships eot~ld~messageswlth nearby stations on other ships or on land. t The Marconi Company hOd also j transmitted messages across the EhQ Jish Channel. By the end of 1901. Mar coni extended the range of his equipmenttospantheAtlan1tcOcean. It was obvlgus. 1hot ~raph ~MeS with subrhatlrie cables and ihelr lnber ent flmltations woUld soon disappear, Ships· at sea would no longer be iso la1ed. No locatlon on Eorth would. be too remote to send and receive mes sages. Clear1y; the opportunity existed tor enormous tiOOnciql gain once Jelio ble equlprrient was avoltable. To that end, 1Uned electrical circuits were developed to reduce the band width of the signals produced by ,the spark transrnlf'tirs. The resonont clfcults were also used in a receiver to select one signal from omong several trans missions. Slm~deslgn principles for resonont ontennas were also being explored and applied, However, the senstflvlty and reUabltlty of the devices used to ctetectthe Wireless signals were still hln cterlng the development of commer () cial wireless-telegraph nefWorks. -

Short Wave Radio
Short Wave Radio A Working Electronic Sculpture Honoring the History of Radio Please note: This radio picks up short wave stations, but for your best satisfaction it will require a little time and attention, both to learn how to operate it and to appreciate the principles and history that it embodies. You’ll find bare-bones instructions on this page and more details inside the notebook. To turn the radio on, rotate the volume control clockwise until you hear a click, then set its dial to 3 or 4. If the radio was not already turned on, you’ll have to wait about 30 seconds for its vacuum tubes to warm up. •Put on the headphones. •Set the radio’s other controls as follows: •RF Gain: Fully clockwise. •Preselector: 1 •Tuning: 20 •Fine Tuning: 5.0 (This works like a clock, only with ten “hours” instead of 12) •Regeneration: 7 (Or advance slowly clockwise from zero until just after the point you hear a louder hiss in the headphones.) •Volume: Set to a comfortable level, usually about 4. Now, slowly adjust the TUNING control back and forth looking for squeals that indicate signals. (The shortwave broadcast band with 31 meter wavelength is located between about 10 and 30 on the dial.) You’ll should find a few unless ionospheric conditions are particularly poor on this day. Leave the TUNING control set on a loud squeal. Then slowly adjust the FINE TUNING to “zero beat.” (You’ll notice as you move the dial across a signal, it starts with a high-pitched note, moving down to a low-pitched or zero note, then back up to high pitch again. -
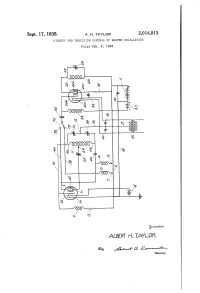
Sept. 17, 1935. A. H. TAYLOR 2,04,913 CIRCUIT for PRECISION CONTRO of MASTER OSCILLATORS Filed Feb
Sept. 17, 1935. A. H. TAYLOR 2,04,913 CIRCUIT FOR PRECISION CONTRO OF MASTER OSCILLATORS Filed Feb. 8, 1933 rvuorvov ALBERT H.TAYLOR &tkow, Patented Sept. 17, 1935 2014,913 UNITED STATES PATENT OFFICE 2,014,913 CIRCUIT FOR PRECISION CONTROL OF MASTER, CSCELLATORS Albert H. Taylor, Washington, D. C., assignor to Wired Radio, Inc., New York, N. Y., a corpora tion of Belaware Application February 8, 1933, Serial No. 655,829 4 Claims. (C. 250-36) My invention relates broadly to high frequency oscillation systems and more particularly to a screen grid electrode of the tetrode Oscillator and circuit for the precision control of master Oscil another of the taps at higher potential leading to lators in a high frequency OScillation System. the plate electrode. A high frequency inductance One of the objects of my invention is to pro system is connected in circuit between the control vide a simplified circuit for a high frequency grid and the anode. A pair of balancing con Oscillation system which is constructed to deliver densers is connected in series across the induc Oscillations of high frequency and efficiency. tance and a connection taken from a midpoint Another object of my invention is to provide between the condensers to a return circuit lead 0. a circuit arrangement for a high frequency OScil ing to the Cathode. Provision is made for con lator and amplifier System having a high degree necting a balance condenser between the Screen O of freedom from variation in frequency brought grid and any point in the coil system. -

A/72-7Ey/ Sept
Sept. 6, 1955 P. POURET METHOD OF DETECTION AND ELECTRIC DETECTOR 2,716,979 OF ACUPUNCTURE AND IGNIPUNCTURE POINTS Filed July 31, l95l 2. Sheets-Sheet l I-1 v-era 72 Aerre A2u re? A/72-7ey/ Sept. 6, 1955 P. POURET 2,716,979 METHOD OF DETECTION AND ELECTRIC DETECTOR OF ACUPUNCTURE AND IGNIPUNCTURE POINTS Filed July 31, l95l 2 Sheets-Sheet 2 J.7 ye-Z/2 - Aerre All ey 2-azé2--- 47/2/12ey United States Patent Office 2,716,979 Patented Sept. 6, 1955 2 drop between the two resistances. 105 and 106 with a 2,716,979. resulting variation in voltage between the plate 101 and the fluorescent screen 102. This variation causes a sector METHOD OF DETECTION ANE).ELECTRIC DE of shadow to appear on the screen, the extent of the dark TECTOR OF ACUPUNCTURE ANE). IGNIPUNC. 5 surface being determined by the difference in potential TURE POINTS occurring between the plate 101 and screen 102. For Pierre Pouret, Chatellerault, France each discharge of the condenser 5, the cathodic eye blinks once only. The sensitivity of the cathodic eye 12 is regu Application July 31, 1951, Serial No. 239,515 lated by potentiometer 14. It should be understood that Claims priority, application France August 3, 1959 0. any equivalent indicating means can be used instead of 13 Claims. (C. 128-e-2.1) electronthe cathode ray eye,indicator. which is also known as a magic eye or In the assembly heretofore described a compromise. between the adjustment of voltage divider 4 and potenti The object of the present invention is the electrical 5 ometer 14 allows contact with the patient in the best detection of particular cutaneous points the location of conditions of sensitivity. -

The Plate Electrode Is What Type of Grounding Electrode? A) Manufactured Grounding Electrode B) Field Assembled Grounding Electr
A) manufactured grounding B) field assembled grounding The plate electrode is what type of grounding electrode? C) in-situ grounding electrode D) artificial grounding electrode electrode electrode When installing an electrical system using Rigid PVC Conduit, what characteristic must be A) has a higher coefficient of B) has a lower coefficient of C) has a lower coefficient of D) has approximately the same considered? expansion than steel expansion than aluminum expansion than steel coefficient of expansion as steel A single dwelling is supplied with electrical power from the local supply authority. The owner of the single dwelling wishes to interconnect his own electrical renewable power system with the local supply authority's system. The owner also wants to use the energy from the renewable A) 120 V B) 80 V C) 50 V D) 46 V system to charge storage batteries for standby power. What is the maximum operating voltage rating of the storage batteries to be used for the standby power system? Which type of enclosure can be used to house a panelboard inside a building that has circulating A) Type 1 B) Type 2 C) Type 4 D) Type 5 metal dust from grinding metal castings? What is the minimum size of RW90XLPE copper conductor that can be installed in a run of EMT that is used to feed the primary of a 75 kVA, dry-type, 600-120/208 V transformer protected by a A) No. 1 AWG B) No. 2 AWG C) No. 3 AWG D) No. 4 AWG moulded case circuit breaker? What is the maximum distance that the disconnecting means for a roof top air make up unit can A) 1 m B) 3 m C) -

Photosensitive Camera Tubes and Devices Handbook
11.2 PHOTOSENSITIVE CAMERA TUBES AND DEVICES 11.1 PHOTOSENSITIVITY / 11.2 11.1.1 Photoemitters / 11.2 11.1.2 Photoconductors / 11.5 11.2 PHOTOELECTRIC-INDUCED TELEVISION SIGNAL GENERATION / 11.5 11.2.1 Photoemission-Induced Charge Images / 11.5 11.2.2 Secondary-Emission-Induced Charge Images / 11.6 11.2.3 Electron-Bombardment-Induced Conductivity / 11.8 11.2.4 Photoconductive-Generated Charge Images / 11.9 11.2.5 Generation of Video Signals by Scanning / 11.11 11.2.6 Low-Velocity Scanning / 11.11 11.2.7 Return-Beam Signal Generation / 11.13 11.2.8 High-Velecity Scanning / 11.14 11.3 EVOLUTION AND DEVELOPMENT OF TELEVISION CAMERA TUBES / 11.14 11.3.1 Nonstorage Tubes / 11.14 11.3.2 Storage Tubes / 11.15 11.4 VIDICON-TYPE CAMERA TUBES / 11.26 11.4.1 Antimony Trisulfide Photoconductor / 11.26 11.4.2 Lead Oxide Photoconductor / 11.28 11.4.3 Selenium Photoconductor / 11.30 11.4.4 Silicon-Diode Photoconductive Target / 11.31 11.4.5 Cadmium Selenide Photoconductor / 11.32 11.4.6 Zinc Selenide Photoconductor / 11.32 11.5 INTERFACE WITH THE CAMERA / 11.33 11.5.1 Optical Input / 11.34 11.5.2 Operating Voltages / 11.34 11.5.3 Dynamic Focusing / 11.36 11.5.4 Beam Blanking / 11.36 11.5.5 Beam Trajectory Control / 11.38 11.5.6 Video Output / 11.40 11.5.7 Deflecting Coils and Circuits / 11.42 11.5.8 Magnetic Shielding / 11.42 11.5.9 Anti-Comet-Tail Tube / 11.42 11.6 CAMERA TUBE PERFORMANCE CHARACTERISTICS / 11.43 11.6.1 Sensitivity and Output / 11.44 11.6.2 Resolution / 11.45 11.6.3 Lag / 11.49 11.6.4 Lag-Reduction Techniques / 11.50 11.7 SINGLE-TUBE COLOR CAMERA SYSTEMS / 11.54 11.7.1 Single-Output-Signal Tubes / 11.55 11.7.2 Multiple-Output-Signal Tubes / 11.58 11.8 SOLID-STATE IMAGER DEVELOPMENT / 11.60 11.8.1 Early Imager Devices / 11.60 11.8.2 Improvements in Signal-to-Noise Ratio / 11.60 11.8.3 CCD Structures / 11.61 11.8.4 New Developments / 11.63 REFERENCES / 11.64 PHOTOSENSITIVITY 11.3 11.1 PHOTOSENSITIVITY A photosensitive camera tube is the light-sensitive device utilized in a television camera to develop the video signal.