Schedule-Based Estimation of Pedestrian Origin-Destination Demand in Railway
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

This Is Freiluft
Alexander Grünig Matthias Zuckschwerdt Martin Klopfenstein Nydeggstalden 30 Architekt M.A. dipl. Architekt FH Architekt M.A. 3011 Bern [email protected] [email protected] [email protected] 031 301 51 51 freiluft.ch This Is Freiluft. „They call themselves Freiluft and refuse to accept strict dogmatics and unhomely austerity. Three young architects from Bern (…) develop their concepts with great enthusiasm and a pinch of humor.“ (Umbauen + Renovieren, 4/2009) „Freiluft’s working methods want to be without mindcuffs but with relish: There are handicrafts (…), sketches, photorealistic renderings, the collage, yes, even the poem…“ (Werk, Bauen + Wohnen, 12/2011) „They care about dialogue between humans, but also between disciplines.“ (Umbauen + Renovieren, 4/2009) Office Freiluft was founded in 2007 by Alexander Grünig, Martin Klopfenstein and Matthias Zuckschwerdt. The sole proprietorship was changed into a limited liability company - Freiluft Architekten GmbH - in 2011. Team Alexander Grünig Associate, Architekt M.A. SIA SWB REG A born 1982 in Bern. Architecture studies in Burgdorf (Switzerland) and Dresden (Germany). Martin Klopfenstein Associate, Architekt M.A. SIA SWB REG A born 1978 in the Swiss Alps. Architecture studies in Mendrisio, Burgdorf und Dresden. Matthias Zuckschwerdt Associate, dipl. Architekt FH SWB, NDK Transcultural Design India born 1980 in Bern. Architecture studies in Burgdorf. Anouk Obermann Architect, Dipl-Ing. born 1988 in Neuilly-sur-Seine (France). Architecture studies in Stuttgart. Memberships SIA . Swiss Society of Engineers and Architects. SWB . Swiss Werkbund Prizes Nomination "Die Besten" 2016 for barn conversion, Rüegsauschachen Recognition Prix Lignum 2012 für House at the Edge of the Woods, Hindelbank Nomination Daylight Award 2010 for loft conversion Schmiedengasse, Burgdorf Nomination Foundation Award 2010 (advancement award for young Swiss architects) Recognition for Good Constructions of the City of Burgdorf 2009 for loft conversion Schmiedengasse, Burgdorf Various prizes in project competitions July 2017 . -

Etat De Vaud
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Infoscience - École polytechnique fédérale de Lausanne EFUF 2014 GREEN CITIES – URBAN NATURE « Crossing Boundaries » 3-7 June 2014, Lausanne, Switzerland 17th European Forum on Urban Forestry www.efuf2014.org CONFERENCE PROGRAMME ( s t a t u s 2 8 / 0 5 / 2 0 1 4 ) REPUBLIQUE ET CANTON DE GENEVE EFUF 2014 | 3-7 June | Lausanne CH | www.efuf2014.org 2/6 Conference Venue and Location The EFUF 2014 will be hosted at the University of Lausanne, Quartier Mouline, IDHEAP (1) and Géopolis (2) Buildings. By train from Lausanne Railway Station > Metro m2 going to "Croisettes" > Change at station "Lausanne-Flon" > Metro m1 going to "Renens CFF" 1 2 > Get off at "UNIL-Mouline" By train from Renens Railway Station > Metro m1 going to "Lausanne Flon" > Get off at "UNIL-Mouline" or > Bus 31 going to "Venoges sud" > Get off at "UNIL-Mouline" By car from the Motorway A1 > Direction "Lausanne-Sud" > Leave at "UNIL-EPFL" 3 > Follow "UNIL-Mouline" Parking Car park "UNIL-Dorigny" (3) is available for participants to the Conference (5 min walk) NO PARKING FOR THE PUBLIC CLOSE TO THE CONFERENCE CENTER !!! Tuesday, 3rd June 2014, Preliminary Programme Preliminary Session: University of Lausanne, Quartier Mouline, Idheap and Géopolis, Ecublens 14:00 - 18:00 FPS COST Action FP1204 - Chair: Carlo Calfapietra Special COST Action FP1204 meeting and workshop (detailed programme in annexe) 18:00 - 19:00 Dislocation Conference Warm Up: Centre Général Guisan, av. Général-Guisan 117-119, Pully (map in annexe) 17:00 - 21:00 Registration for EFUF participants 19:00 - 20:00 Welcome Addresses Yves Kazemi, Chairman EFUF 2014 Dr. -
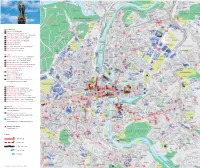
Tram with Stop Bus with Stop Rail Line with Station Public Building Park+Ride Legends Places of Interest 1 Bear Park, Line 12
Places of interest 1 Bear Park, line 12: Bärenpark 2 Parliament House and Parliament Square, lines 6, 7, 8, 9, 12: Bärenplatz; lines 10, 19: Bundesplatz 25 18 3 French Church, lines 6, 7, 8, 9, 12: Zytglogge 4 Church of the Holy Spirit, all lines: Bahnhof 5 Prison Tower, lines 6, 7, 8, 9, 12: Bärenplatz 6 Cathedral, line 12: Rathaus 7 Town Hall, line 12: Rathaus 8 Clock Tower, lines 6, 7, 8, 9, 10, 12, 19: Zytglogge 9 Einstein’s House, line 12: Rathaus 10 Nydegg Bridge, line 12: Nydegg 24 Museums 11 Museum of Fine Arts, lines 6, 7, 8, 9, 12: Bärenplatz lines 11, 20, 21: Bollwerk 12 Zentrum Paul Klee, line 12: Zentrum Paul Klee 13 Kunsthalle, lines 6, 7, 8, 19: Helvetiaplatz 14 Natural History Museum, lines 6, 7, 8, 19: Helvetiaplatz 15 Bernisches Historisches Museum/Einstein Museum (Historical Museum of Bern), lines 6, 7, 8, 19: Helvetiaplatz 16 Swiss Alpine Museum, lines 6, 7, 8, 19: Helvetiaplatz 19 17 Museum of Communication, 22 lines 6, 7, 8, 19: Helvetiaplatz 11 18 YB Museum (Young Boys’ Football Club Museum), line 9: Wankdorf Center, line 20: Wyler 12 Recreation/sport 3 19 7 Botanical Gardens, line 20: Gewerbeschule 5 10 20 Elfenau Municipal Gardens, line 19: Luternauweg 8 4 9 21 Gurten recreational area, line 9: Gurtenbahn 28 6 1 22 Rose Garden, line 10: Rosengarten 27 2 23 Dählhölzli Zoological Gardens, line 19: Tierpark 24 BERNEXPO, PostFinance-Arena, line 9: Guisanplatz Expo 25 Stade de Suisse Wankdorf, line 9: Guisanplatz Expo 26 Bernaqua/Westside, line 8: Brünnen Westside Bahnhof 26 16 13 Information 27 The BERNMOBIL Libero-Shop, -

Postal Markings and Cancellations in Switzerland & Liechtenstein
Postal Markings and Cancellations in Switzerland & Liechtenstein Forward Shortly after this document was completed, a separate handbook on Swiss Railway Postmarks, by Alfred Müller and Roy Christian was published in 1977. In this more recent publication, Müller and Christian list the Travelling Post Office (TPO) cancellations according to the groupings recorded in the earlier handbook of Swiss Postal Cancellations “Grosses Handbuch der Schweizer Abstemplungen”, by Andres & Emmenegger. In recent years this latter publication has become known in its abbreviated form “Abstempelungs-Werk”, or simply “AW”. Felix Ganz, the author of the edited version you are about to read, used his own numbering system to describe the various different Key Types and Sub-Types of railway post office cancellations he had encountered. For the benefit of student philatelists interested in the Swiss Travelling Post Office, I have included the corresponding AW Group and Type alongside Felix’s original recordings. These appear in parentheses, in red bold type, e.g. (AW 83C/1) Every effort has been made to ensure accuracy from the original article, with additional information inserted wherever appropriate. The Helvetia Philatelic Society would welcome comments on this and any other article published on their website www.swiss-philately.co.uk Please address your correspondence to the Society’s webmaster at: [email protected] Published by the Helvetia Philatelic Society (Great Britain) Page 1 Postal Markings and Cancellations in Switzerland & Liechtenstein RAILWAY & STATION MARKINGS By Felix Ganz A coverage of several aspects of rail cancellations in Switzerland (there are none to speak of in Liechtenstein except for the Austrian railway from Buchs in Switzerland to Feldkirch in Austria that once upon a time stopped in Liechtenstein to pick up mail posted at the three stations, and then cancelled them with the Austrian TPO marks in use at that time) has been attempted and successfully achieved, but a complete picture of ALL aspects is yet to be written. -

Artigas, Chapallaz, De Montmollin Bards of Enamels
Press release February 2015 Artigas, Chapallaz, de Montmollin Bards of Enamels MUSÉE ARIANA, GENEVA, 4 FEBRUARY TO 31 MAY 2015 Inauguration Tuesday, February 3, 2015 10, avenue de la Paix 1202 Genève To download : www.ariana-geneve.ch Un musée Ville de Genève www.ariana-geneve.ch Artigas, Chapallaz,de Montmollin Bards of Enamels MUSÉE ARIANA, GENEVA, 4 FEBRUARY TO 31 MAY 2015 PRESS RELEASE Geneva, February 2015 Combining in a single exhibition works by the Catalan Josep Llorens Artigas (1892-1980), the Swiss ceramists Édouard Chapallaz (b.1921) and Brother Daniel de Montmollin (b.1921) – active within the Taizé religious community in Burgundy – is not purely random. These three artists, who have each in their own way left their mark on contemporary European ceramics, have continuously enhanced their understanding of enamels throughout their careers, knowledge that all three have been keen to pass on through their teaching, publications and more generally by their openness and their availability towards colleagues. Creating unique wheel-turned pieces, mostly with simple, pure lines, all three have endeavoured to sublimate these forms by clothing them, like a skin intimately fused to the clay, with enamels of infinite variety and depth. Bright or muted, matt or gloss, single or superimposed, fired in reduction or oxidation atmospheres, the enamels have an eloquence that is never, with these highly experienced masters, the result of chance. Fire certainly plays a major role and can sometimes have surprises in store, but it is mainly through knowledge, practice and experience – “a kiln without tests is a wasted kiln” said Artigas – the fruit of many years of hard work, that they have acquired over time a remarkable command of their art. -

Lausanne-By-Bike.Pdf
Infos Pratiques N’oubliez pas de télécharger la carte de l’itinéraire sur Lausanne by bike www.lesbaladeurs.ch Thème A sightseeing tour Histoires Difficulté Tous mollets Durée 1h-2h Itinéraire The esplanade of the cathedral - The cathedral - The “Place du château” - The park of Mon-Repos - The "Place Saint-François" - The “Place de la Palud” - On the bridge over the Flon - The esplanade of Montbenon - The “Vallée de la Jeunesse” - Ouchy Prêts de vélos Prêt de vélo gratuit 7j/7 de 7h30 à 21h30 contre caution de 20 CHF et présentation d’une pièce d’identité. Lausanne Roule - sous les arches du Grand-Pont. 36 Lausanne by bike Lausanne by bike by Lausanne 35 2 bike by Lausanne se développeront ! développeront se d’usagers, mieux ils se feront respecter et plus les aménagements les plus et respecter feront se ils mieux d’usagers, vaut la peine de persévérer, car plus il y aura d’usagères et d’usagères aura y il plus car persévérer, de peine la vaut la route s’apprend, même lorsqu’il n’y a pas de piste cyclable. Cela cyclable. piste de pas a n’y lorsqu’il même s’apprend, route la périlleux, mais tout est question d’habitude ! Prendre sa place sur place sa Prendre ! d’habitude question est tout mais périlleux, pour l’environnement !Le vélo en ville peut sembler un exercice un sembler peut ville en vélo !Le l’environnement pour mode de déplacement, vous faites un geste pour votre santé et santé votre pour geste un faites vous déplacement, de mode Cette balade a été conçue pour s’effectuer à vélo. -

Mobility One-Way: It Allows for One-Way Journeys Between All Manner of Different Towns and Cities Throughout Switzerland
PRESS RELEASE Rotkreuz, 4 April 2019 Mobility is doubling its One-Way network Travel from place to place – and simply leave the car where it is: now possible between 29 Mo- bility stations throughout all of Switzerland, now including Aarau, Baden, Geneva, Lausanne, Neuchâtel, Fribourg, Biel and multiple stations in Zurich. Mobility is continually expanding its variety of services. One solution particularly popular with almost 200’000 customers is Mobility One-Way: it allows for one-way journeys between all manner of different towns and cities throughout Switzerland. Mobility has now correspondingly increased the number of stations to around 30. Mobility Communication Officer Patrick Eigenmann is delighted about the devel- opment: “The expansion means that even more people will be able to travel easily and conveniently from A to B in the future. For our customers, One-Way is the ideal supplement to the standard Mobility offer and to our urban free-floating models such as Mobility Scooter. A subscription gives you a wide variety of mobility options at your disposal.” From A for Aarau to Z for Zurich From today onwards, the following stations are now part of the Mobility One-Way network: Aarau Rail- way Station, Baden Brown Boveri Platz, Biel Railway Station, Fribourg Railway Station, Écublens EPFL/Parking Rivier, Geneva Cornavin Railway Station, Lausanne Railway Station, Neuchâtel Railway Station, Nyon Railway Station, Rapperswil-Jona Railway Station, Uster Railway Station, Yverdon Rail- way Station, Zurich Hardbrücke Railway Station, Zurich Tiefenbrunnen Railway Station and Zurich Woll- ishofen Railway Station. They are supplementing the existing station network comprising: Basel Railway Station, Basel Airport, Bern Railway Station, Lucerne Railway Station, Olten Railway Station, Rotkreuz Suurstoffi, Solothurn Railway Station, St. -

Schedule-Based Estimation of Pedestrian Demand Within a Railway Station
Schedule-based estimation of pedestrian demand within a railway station Flurin Hänseler Nicholas Molyneaux Michel Bierlaire Amanda Stathopoulos Transport and Mobility Laboratory, EPFL May 2014 Schedule-based estimation of pedestrian demand within a railway station May 2014 Transport and Mobility Laboratory, EPFL Schedule-based estimation of pedestrian demand within a railway station Flurin Hänseler, Nicholas Molyneaux, Michel Bierlaire, Amanda Stathopoulos {flurin.haenseler,nicholas.molyneaux,michel.bierlaire,amanda.stathopoulos}@epfl.ch May 1, 2014 Abstract A framework is outlined for estimating pedestrian demand within a railway station which takes advantage of the train timetable and train frequentation data, as well as various direct or indirect indicators of demand. These may include e.g. link flow counts, measurements of density and travel times, or historical information. The problem is considered in discrete time and at the aggregate level, i.e., for groups of pedestrians associated with the same origin-destination pair and with the same departure time interval. The formulation of the framework allows for a wide applicability to various types of railway stations and input data. A preliminary case study analysis of Lausanne railway station provides an example of such an application. Cover photo: Michael Buholzer, c Reuters Keywords Demand estimation, pedestrian flows, schedule-based estimation, public transport i Schedule-based estimation of pedestrian demand within a railway station May 2014 1 Introduction The demand for mobility is increasing at a fast pace, and so is the volume of traffic in general. Taking the network of the Swiss Federal Railways (SBB) as an example, the number of daily transported passengers has grown by approximately 50% in the last decade alone (Amacker, 2012). -

Capital Switzerland Contents
Berne capital Switzerland Contents 1 Bern 1 1.1 Name ................................................. 1 1.2 History ................................................. 1 1.2.1 Early history ......................................... 1 1.2.2 Old Swiss Confederacy .................................... 2 1.2.3 Modern history ........................................ 2 1.3 Geography ............................................... 2 1.3.1 Climate ............................................ 3 1.3.2 Subdivisions .......................................... 3 1.4 Demographics ............................................. 3 1.5 Historic population .......................................... 4 1.6 Politics ................................................. 4 1.7 Main sights .............................................. 4 1.7.1 Heritage sites of national significance ............................. 5 1.8 Culture ................................................ 5 1.8.1 Theatres ............................................ 5 1.8.2 Cinemas ............................................ 6 1.8.3 Film festivals ......................................... 6 1.8.4 Festivals ............................................ 6 1.8.5 Fairs .............................................. 6 1.9 Sport .................................................. 6 1.10 Economy ............................................... 7 1.11 Religion ................................................ 7 1.12 Education ............................................... 7 1.13 Transport .............................................. -

Köniz Wabern Länggasse Mattenhof Breitenrain Lorraine Marzili Elfenau
Deisswil bei Münchenbuchsee Zuzwilerstrasse Wiggiswil Lyssst rasse Lyssst rasse gasse oos M Hofwilstrasse Bernstra Schüpbergstrasse rasse Hä Schöneggwe Münchenbuchssee est uslimoss sse g Mühl Kohlholzweg s trasse fstrasse Fell Oberdor e nber gs Oberdorfstrasse trass e Diemerswil Talstr. Büchsistrasse Bodenackerweg Dorfstrasse Bernstra Grächwil sse Hofwilstrasse Leut Bernstrass sche nstrasse e Waldeck e rass ilst ächw Gr Meikirch Zürichstrasse e Bernstrasse Wahlendorfstrass ilstrasse Bernstrasse w Moosgasse sse a r Diemers Aussendrofst asse ilstr sw Wahlendorf e Säri Wahlendorfstrass Oberlindach hlindachstrasse Lindachstrasse Kirc se Kirchlindachstra Allmendstras e L g eut e ss sse Wahlendorfstr. schenst tra s Jetzikofen ämisw R Alpen rasse Zollikofen Grauholzstrasse Moostrasse Bernstrasse Kirchlindach sse Birkens chstra Stockhornstrasse trasse Linda Hubelweg Gantrischstr asse Eichenweg rasse sse Weissenstein Langbarenst ernstra B sse rstra e Fische rass sse rgst Hangstra Aarbe Heimenhausstrasse Kreu zst Ortschwaben Hubel r. ergstrasse Innerb sse Mittelstrasse ra Niederlindach Bernst Lindachstrasse Wölflifriedstrasse Innerbe Staatsstrasse r gstrasse Meikirchstr Staatsstrasse Mittelstrasse Wahlendorfstr. Wahlac asse kerstrass Meikirchstrasse e Schärgummenstr. se istras ere Molk Hirschere Postgasse Aarbergstrasse Staatsstr ass se asse e as Staatsstr str riswilstrasse Mö Reichenbach R edernstrasse ü tis Ri tr Staatsstrasse as se Uettligenstrasse 1.00.80.60.40.20.0 se Bremgartenstrasse trasse Grundfelds Grauholzstras Möriswilstrasse Säriswilstr. M Ortschwabenstr. eikirchstr Bernstras Uettligen asse Aarestrasse se Krauchhalstrasse Wohlenstrasse Lochholzstrasse rasse Schlupfstrasse Dorfst Dorfstrasse rasse Grundfeldst asse igenstr Uettl enstr. Murzelenstrasse tt Alte Altikofe Zul te nstrasse e G Ti l Chasseralstrasse igerstras abs ra efena ass Riedhaus H r u ho alst ust se lzstr ra sse as Krauchh e se strass den Juras B Mö Rie trasse eundenstr. -

Esoa Preliminary Program
EUROPEAN SCHOOL OF ANTENNAS Analysis of Planar and Conformal Antennas February 27 – March 3, 2006 EPFL, Lausanne, Switzerland Involved institutions: EPFL-CHALMERS-ERICSSON-KUL-KTH-U. Belgrade Final Programme Doctoral School Programme The ACE Doctoral School of Antennas takes place from February 27 to March 3, 2006 on the campus of the EPFL, Lausanne, Switzerland and it is dedicated to the Analysis of Planar and Conformal antennas. This course will cover the theoretical aspects of the analysis and design of planar and conformal antennas. The first half of the course will deal with the fundamentals of the mathematical and electromagnetic models being used for the analysis of printed antennas. The second half will cover analysis methods for antennas embedded in multilayer structures of planar, circular, cylindrical and spherical types, with real-life applications. All lectures will be held in the room CO017 and the exercises in the computer room ELD020. TEACHERS: • Prof. J. R. Mosig (EPFL, Switzerland) • Prof. P.-S. Kildal (Chalmers, Sweden) • Prof. Z. Šipuš (Chalmers, Sweden) • Prof. G. Vandenbosch (KUL, Belgium) • Prof. A. R. Djordjević, EPFL Invited Lecturer (Univ. Belgrade, Serbia) • Dr. S. Raffaelli (Ericsson, Sweden) • Dr. P. Persson (KTH, Sweden) 2/16 SCHEDULE Monday February 27th (Room CO 017) 08:00-10:00 Introduction to Integral Equations for printed structures. Field and potential- based formulations. Space and Spectral domains. Lecturer: J. R. Mosig 10:00-12:00 Green's functions for printed antennas. Numerical techniques. Computation of macroscopic circuit quantities. Lecturer: J. R. Mosig 12:00-14:00 Lunch at Le Vinci 14:00-17:00 Self-study and assignments Lecturer: J. -

Modeling Pedestrian Flows in Train Stations: the Example of Lausanne
Modeling pedestrian flows in train stations: The example of Lausanne railway station Flurin S. Hänseler Michel Bierlaire Nicholas A. Molyneaux Riccardo Scarinci Michaël Thémans École polytechnique fédérale de Lausanne (EPFL) April 2015 15th Swiss Transport Research Conference STRC Monte Verità / Ascona, April 15 – 17, 2015 Modeling pedestrian flows in train stations: The example of Lausannerailwaystation April2015 Transport and Mobility Laboratory School of Architecture, Civil and Environmental Engineering EPFL – Ecole Polytechnique Fédérale de Lausanne Modeling pedestrian flows in train stations: The example of Lausanne railway station Flurin S. Hänseler, Michel Bierlaire, Nicholas A. Molyneaux, Riccardo Scarinci, Michaël Thémans April 2, 2015 Abstract In collaboration with the Swiss Federal Railways (SBB-CFF-FFS), various challenges associ- ated with pedestrian flows in train stations are discussed at the example of Lausanne railway station. For this site, a rich set of data sources including travel surveys, pedestrian counts and trajectories has been collected. The report is organized in three parts. First, an empirical analysis of the aforementioned data sources is provided. The main focus thereby lies on the identification of periodical movement patterns both in time and in space. Second, a methodology for estimating pedestrian origin- destination (OD) demand using various information sources including the train timetable is discussed. This methodology is applied to the case of Lausanne railway station, and results are provided for the morning peak period. Third, a pedestrian flow model is presented which, for a given OD demand, allows to estimate pedestrian travel times and density levels based on an empirical pedestrian fundamental diagram. This model is applied to study pedestrian movements in an underpass of Lausanne railway station, including an assessment of pedestrian level of service.