DOCSLIB.ORG

Systems and Units

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Systems and Units Systems and Units The three systems of units are: 1. The English or the ft-lb-s System 2. The International or the m-kg-s System 3. The Laboratory or the cm-gm-s System Quantities fall into two main categories: 1. Principal Quantities Length (L) Mass (m) Time (t) Angle (θ) Temperature (T) 2. Derived Quantities Area (A) Volume (V) Velocity (ν) Frequency (Hz.) Acceleration (a) Angular Velocity (ω) Angular Acceleration (â) Volume Flow Rate (q) o Mass Flow Rate ( m ) Density (ρ) Specific Gravity (SG) Force (F) Force due to Inertia (FI) Force due to Gravity (FG) Force due to Viscosity (Fµ) Force due to Elasticity (FE) Force due to Pressure (FP) Specific Weight (γ) Energy (E) Moment of a Force (M) Work (W) Pressure (p) Stress (τ) Power (P) Dynamic Viscosity (µ) Kinematic Viscosity (ν) 1 1. Principal Quantities Quantity English System International System mile (mi) = 1760 yd kilometer (km) = 1000 m Length yard (yd) = 3 ft meter (m) = 100 cm foot (ft) = 12 in centimeter (cm) inch (in) = 2.54 cm Mass slug (sl) = 32.17404856 lbm kilogram (kg) = 1000 gm pound mass (lbm) = 453.592370 gm gram (gm) year = 365 d year = 365 d Time day = 24 h day = 24 h hour = 60 m hour = 60 m minute = 60 s minute = 60 s 1 rev. = 2B radians = 360E 1 rev. = 2B radians = 360E Angle 1 r = 57.29578E 1 r = 57.29578E 1 E = 0.017453r 1 E = 0.017453r Ordinary EF= 1.8EC+32 Ordinary EC= (EF-32)/1.8 Temperature Absolute ER= EF+459.688 Absolute K= EC+273.16 ER= 1.8 K K= ER/1.8 2 2. Derived Quantities Quantity Formula English Units SI Units Lab. Units mi2, ft2, in2, acre cm2, darcy, md Area A = L2 1 mi2 = 640 acres m2 1 cm2 = 1 acre = 43,560 101,320,790 d ft2 1 d = 1000 md bbl, ft3, gal, qt m3, ltr Volume V = L3 bbl = 5.6146 ft3 m3 = 1000 ltr cm3 = cc bbl = 42 gal ltr = 1000 cc gal = 4 qt = 3.785 ltr dL Velocity ν = ft/s m/s cm/s dt Frequency Hz. s-1 s-1 s-1 dν Acceleration a = ft/s2 m/s2 cm/s2 dt Angle 2 rad and E rad and E rad and E 360E = 2B rad 360E = 2B rad 360E = 2B rad dθ Angular ω = rad/s rad/s rad/s Velocity dt dω Angular aˆ = rad/s2 rad/s2 rad/s2 Acceleration dt Volume dV q = bbl/d, ft3/s m3/s, ltr/s cc/s Flow Rate dt o dm Mass Flow m = slug/s, lbm/s kg/s gm/s Rate dt m Density ρ = slug/ft3, lb/ft3, kg/m3 gm/cc V lb/gal Dw = 1.940 ρ 3 SG = f = slug/ft 3 Specific ρw Dw = 62.428 Dw= 10 Dw = 1 gm/cc 3 Gravity 141.5 lbm/ft3 kg/m 131.5+oAPI Dw = 8.345 lbm/gal Dw = 0.433 psi/ft Dw = 10 EAPI 3 2. Derived Quantities (cont.) Quantity Formula English Units SI Units Lab. Units Force F = m a lbf = slug ft/s2 N = kg m/s2 dyne = gm cm/s2 lbf = 444,822 dyne 1 N = 105 lbf = 4.44822 N dynes Force due to FI = m a lbf N dyne Inertia Force due to FG = m g lbf N dyne Gravity=Wt. g = 32.17404856 g = 9.80665 g = 980.665 ft/s2 m/s2 cm/s2 dν Force due to Fµ = µ A lbf N dyne Viscosity dy Force due to FE = E A lbf N dyne Elasticity Force due to FP = p A lbf N dyne Pressure 3 3 Specific Wt. ( = FG/V lbf/ft N/m dyne/cc Energy E = F L lbf-ft J = N-m erg = dyne cm Moment of a M = F L lbf-ft J erg = dyne cm Force Work W = F L lbf-ft J erg = dyne cm 2 2 2 2 Pressure p = FN/A lbf/ft , lbf/in = psi Pa = N/m dyne/cm 5 psc = 14.69594877 bar = 10 Pa psc=1013250 2 psi psc = 1.01325 d/cm bar psc = 1 atm psc = 101325 psc = 76 cm Hg Pa 2 2 2 Stress J = FT/A lbf/ft , lbf/in = psi bar, Pa dyne/cm Power P = E/t lbf-ft/s, hp W = J/s erg/s 1 hp = 550 lbf-ft/s F Dynamic µ lbf-s/ft2 = 47,880 N s/m2= 10 dyne s/cm2 = Fµ = Viscosity dν / dyA cp poise poise N s/m2= 1000 1 poise = 100 cp cp Kinematic < = µ/D ft2/s = 929 stoke m2/s = 104 cm2/s = stoke Viscosity stoke 4 EPS-441: Petroleum Development Geology Units and Conversion Semester: Homework #: Name: SS#: Problem #1: Do the following unit conversions: From To 38 oAPI lb/ft3 12 oAPI SG 56 oAPI psi/ft 40 oAPI SG 28 oAPI gm/cc 31 oAPI psi/ft 0.433 psi/ft lb/ft3 0.433 psi/ft lb/gal 0.433 psi/ft gm/cc 0.378 psi/ft oAPI 0.394 psi/ft oAPI SG = 0.76 psi/ft SG = 1.10 psi/ft SG = 0.74 lb/ft3 SG = 1.08 lb/gal SG = 0.88 oAPI 48.8 lb/ft3 SG 62.4 lb/ft3 oAPI 64.3 lb/ft3 psi/ft 48.7 lb/ft3 gm/cc 10.86 lb/gal gm/cc 8.33 lb/gal psi/ft 8.33 lb/gal lb/ft3 10.4 lb/gal gm/cc 0.82 gm/cc SG 1.02 gm/cc psi/ft 0.87 gm/cc psi/ft 0.91 gm/cc lb/ft3 Problem #2: Given a rectangular solid with dimensions 1000 ft x 400 ft x 40 ft. Calculate its volume in ft3, bbl, acre-ft?. 5 Problem #3: Calculate pressure gradients of the following liquids: SG = 1.00 3 Dw = 66.3 lb/ft SG = 1.15 Dw = 9.5 lb/gal SG = 0.85 EAPI = 42 EAPI = 32 EAPI = 45 3 Do = 58.1 lb/ft Problem #4: A well drilled to 3000 ft penetrates a formation containing 28 EAPI oil. If reservoir pressure is 1300 psia, what is the shut-in surface pressure?. If reservoir pressure is 1000 psia, how many ft of oil will be standing in the wellbore?. Problem #5: In an area where ambient temperature is 78 EF, two wells, A and B, were drilled. The depth of well A is 7250 ft and the depth of well B is 8000 ft. The bottom hole temperature (BHT) in well B is 180 EF. What is the BHT in well A?. Problem #6: The areal extent of a reservoir as determined with seismic data is 1500 acres. From logs the following reservoir properties were determined: Zone N h, ft Sw 1 0.28 4 0.28 2 0.32 7 0.40 3 0.18 3 0.31 4 0.20 11 0.27 a) Calculate the pore volume in the reservoir. Give your answers in acre-ft, ft3, and bbl. b) Calculate the volume of oil in the reservoir. Give your answers in acre-ft, ft3, and bbl. c) Calculate the STB of oil if Bo = 1.34 RB/STB. 6 Problem #7: The average reservoir properties of a 300 acre reservoir are: N = 18% and Sw = 36%. Estimated volume of oil originally in place = 410 MM STB. Formation thickness = 2000 ft. Determine the oil formation volume factor. Problem #8: Consider the sketch below. Given EAPI of oil = 35. water SG = 1.07. If well A penetrates the oil zone, find the shut-in surface pressure at well A?. 7 EPS-441: Petroleum Development Geology Units and Conversion Semester: Homework #: Name: SS#: Problem #1: A reservoir has an areal extent of 500 acres, an average thickness of 90 ft, and an average porosity of 20%. a) What is the reservoir volume available for hydrocarbons?. Answer in acre-ft, bbl, and ft3. b) If the average water saturation is 35%, what is the reservoir volume available for oil?. Answer in acre-ft, bbl, and ft3. c) Same as (b) except reservoir fluid is gas. d) If Bo = 1.34 RB/STB. What is the oil volume from (b) in surface barrels?. in surface cubic feet?. e) If Bg = 310 SCF/CF. What is the gas volume from (c) in surface cubic feet?. in surface barrels?. Problem #2: A well is being drilled to a depth of 10,000 ft. The wellbore diameter is 9 inches. The drill string has an inside diameter of 4.5 inches and an outer diameter of 5 inches. What is the volume of mud in the hole when it is at total depth (TD) and there is a complete drill string in the hole?. Ignore collars and bit volume and assume the mud is incompressible. Answer in cubic feet and barrels. 8 Problem #3: Data for the diagram shown below are: a) oil gravity = 38 EAPI b) water specific gravity = 1.05 c) average gas gradient = 0.055 psi/ft d) only oil flows in oil zone e) reservoir B is in water communication with the surface f) pressure at oil zone datum in reservoir A = 3820 psig g) temperature gradient = 1.5 EF/100 ft. h) mean surface temperature = 61 EF i) ground level is 3000 ft above sea level j) elevations given are sub-sea but answers should be in subsurface a) Calculate pressure and temperature at each of the 7 zones indicated in the diagram.
Load more

Recommended publications
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • S.I. and Cgs Units
    Some Notes on SI vs. cgs Units by Jason Harlow Last updated Feb. 8, 2011 by Jason Harlow. Introduction Within “The Metric System”, there are actually two separate self-consistent systems. One is the Systme International or SI system, which uses Metres, Kilograms and Seconds for length, mass and time. For this reason it is sometimes called the MKS system. The other system uses centimetres, grams and seconds for length, mass and time. It is most often called the cgs system, and sometimes it is called the Gaussian system or the electrostatic system. Each system has its own set of derived units for force, energy, electric current, etc. Surprisingly, there are important differences in the basic equations of electrodynamics depending on which system you are using! Important textbooks such as Classical Electrodynamics 3e by J.D. Jackson ©1998 by Wiley and Classical Electrodynamics 2e by Hans C. Ohanian ©2006 by Jones & Bartlett use the cgs system in all their presentation and derivations of basic electric and magnetic equations. I think many theorists prefer this system because the equations look “cleaner”. Introduction to Electrodynamics 3e by David J. Griffiths ©1999 by Benjamin Cummings uses the SI system. Here are some examples of units you may encounter, the relevant facts about them, and how they relate to the SI and cgs systems: Force The SI unit for force comes from Newton’s 2nd law, F = ma, and is the Newton or N. 1 N = 1 kg·m/s2. The cgs unit for force comes from the same equation and is called the dyne, or dyn.
    [Show full text]
  • SI and CGS Units in Electromagnetism
    SI and CGS Units in Electromagnetism Jim Napolitano January 7, 2010 These notes are meant to accompany the course Electromagnetic Theory for the Spring 2010 term at RPI. The course will use CGS units, as does our textbook Classical Electro- dynamics, 2nd Ed. by Hans Ohanian. Up to this point, however, most students have used the International System of Units (SI, also known as MKSA) for mechanics, electricity and magnetism. (I believe it is easy to argue that CGS is more appropriate for teaching elec- tromagnetism to physics students.) These notes are meant to smooth the transition, and to augment the discussion in Appendix 2 of your textbook. The base units1 for mechanics in SI are the meter, kilogram, and second (i.e. \MKS") whereas in CGS they are the centimeter, gram, and second. Conversion between these base units and all the derived units are quite simply given by an appropriate power of 10. For electromagnetism, SI adds a new base unit, the Ampere (\A"). This leads to a world of complications when converting between SI and CGS. Many of these complications are philosophical, but this note does not discuss such issues. For a good, if a bit flippant, on- line discussion see http://info.ee.surrey.ac.uk/Workshop/advice/coils/unit systems/; for a more scholarly article, see \On Electric and Magnetic Units and Dimensions", by R. T. Birge, The American Physics Teacher, 2(1934)41. Electromagnetism: A Preview Electricity and magnetism are not separate phenomena. They are different manifestations of the same phenomenon, called electromagnetism. One requires the application of special relativity to see how electricity and magnetism are united.
    [Show full text]
  • Magnetic Units
    Magnetic Units Magnetic poles, moments and magnetic dipoles The famous inverse square force law between two poles p1 and p2 separated by a distance r was discovered by the English scientist John Michell (1750), and the French scientist Charles Coulomb (1785): In the cgs (electromagnetic) system, k = 1, and the interaction force between two poles each of unit strength (in emu) separated by 1 cm is equal to 1 dyne. Alternatively, one can visualize this force as an interaction force between the pole p0 and the field H produced by another other pole of strength p: Therefore, the field produced by p at the location of p0 a distance r away is given by: The unit of the magnetic field, the Oersted (Oe), is defined as the strength of the field produced by a unit pole at a point 1 cm away (by eq. 3). Alternatively, it is the strength of the field which exerts a force of 1 dyne of a unit pole (by eq. 2). Faraday’s representation Michael Faraday represented the field strength in terms of “lines of force” (1 line of force = 1 maxwell (= 1 Mx)). In this representation, the field strength is defined as the number of lines of force passing through a unit area normal to the field. Therefore: 1 Oe = 1 line of force/cm2 = 1 Mx/cm2 (4) A bar magnet has a magnetic moment given in terms of the pole strength and length of the magnet by: The unit of the magnetic moment in cgs system is emu = erg/Oe. It is worth mentioning that the magnetic pole does not exist, neither can the distance between the two poles be determined accurately due to non-localization of the pole.
    [Show full text]
  • The International System of Units (SI) - Conversion Factors For
    NIST Special Publication 1038 The International System of Units (SI) – Conversion Factors for General Use Kenneth Butcher Linda Crown Elizabeth J. Gentry Weights and Measures Division Technology Services NIST Special Publication 1038 The International System of Units (SI) - Conversion Factors for General Use Editors: Kenneth S. Butcher Linda D. Crown Elizabeth J. Gentry Weights and Measures Division Carol Hockert, Chief Weights and Measures Division Technology Services National Institute of Standards and Technology May 2006 U.S. Department of Commerce Carlo M. Gutierrez, Secretary Technology Administration Robert Cresanti, Under Secretary of Commerce for Technology National Institute of Standards and Technology William Jeffrey, Director Certain commercial entities, equipment, or materials may be identified in this document in order to describe an experimental procedure or concept adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the entities, materials, or equipment are necessarily the best available for the purpose. National Institute of Standards and Technology Special Publications 1038 Natl. Inst. Stand. Technol. Spec. Pub. 1038, 24 pages (May 2006) Available through NIST Weights and Measures Division STOP 2600 Gaithersburg, MD 20899-2600 Phone: (301) 975-4004 — Fax: (301) 926-0647 Internet: www.nist.gov/owm or www.nist.gov/metric TABLE OF CONTENTS FOREWORD.................................................................................................................................................................v
    [Show full text]
  • Chemical Engineering Vocabulary
    Chemical Engineering Vocabulary Maximilian Lackner Download free books at MAXIMILIAN LACKNER CHEMICAL ENGINEERING VOCABULARY Download free eBooks at bookboon.com 2 Chemical Engineering Vocabulary 1st edition © 2016 Maximilian Lackner & bookboon.com ISBN 978-87-403-1427-4 Download free eBooks at bookboon.com 3 CHEMICAL ENGINEERING VOCABULARY a.u. (sci.) Acronym/Abbreviation referral: see arbitrary units A/P (econ.) Acronym/Abbreviation referral: see accounts payable A/R (econ.) Acronym/Abbreviation referral: see accounts receivable abrasive (eng.) Calcium carbonate can be used as abrasive, for example as “polishing agent” in toothpaste. absorbance (chem.) In contrast to absorption, the absorbance A is directly proportional to the concentration of the absorbing species. A is calculated as ln (l0/l) with l0 being the initial and l the transmitted light intensity, respectively. absorption (chem.) The absorption of light is often called attenuation and must not be mixed up with adsorption, an effect at the surface of a solid or liquid. Absorption of liquids and gases means that they diffuse into a liquid or solid. abstract (sci.) An abstract is a summary of a scientific piece of work. AC (eng.) Acronym/Abbreviation referral: see alternating current academic (sci.) The Royal Society, which was founded in 1660, was the first academic society. acceleration (eng.) In SI units, acceleration is measured in meters/second Download free eBooks at bookboon.com 4 CHEMICAL ENGINEERING VOCABULARY accompanying element (chem.) After precipitation, the thallium had to be separated from the accompanying elements. TI (atomic number 81) is highly toxic and can be found in rat poisons and insecticides. accounting (econ.) Working in accounting requires paying attention to details.
    [Show full text]
  • Units of Measure Used in International Trade Page 1/57 Annex II (Informative) Units of Measure: Code Elements Listed by Name
    Annex II (Informative) Units of Measure: Code elements listed by name The table column titled “Level/Category” identifies the normative or informative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative = Units of count and other units of measure (invariably with no comprehensive conversion factor to SI) The code elements for units of packaging are specified in UN/ECE Recommendation No. 21 (Codes for types of cargo, packages and packaging materials). See note at the end of this Annex). ST Name Level/ Representation symbol Conversion factor to SI Common Description Category Code D 15 °C calorie 2 cal₁₅ 4,185 5 J A1 + 8-part cloud cover 3.9 A59 A unit of count defining the number of eighth-parts as a measure of the celestial dome cloud coverage. | access line 3.5 AL A unit of count defining the number of telephone access lines. acre 2 acre 4 046,856 m² ACR + active unit 3.9 E25 A unit of count defining the number of active units within a substance. + activity 3.2 ACT A unit of count defining the number of activities (activity: a unit of work or action). X actual ton 3.1 26 | additional minute 3.5 AH A unit of time defining the number of minutes in addition to the referenced minutes. | air dry metric ton 3.1 MD A unit of count defining the number of metric tons of a product, disregarding the water content of the product.
    [Show full text]
  • 1 Basic Electromagnetism
    Cambridge University Press 978-0-521-44964-9 - Magnetic Memory: Fundamentals and Technology Denny D. Tang and Yuan-Jen Lee Excerpt More information 1 Basic electromagnetism 1.1 Introduction Two thousand years ago, the Chinese invented the compass, a special metallic needle with one end always pointing to the North Pole. That was the first recorded human application of magnetism. Important understandings and developments were achieved in the mid 19th century and continue into the present day. Indeed, today, magnetic devices are ubiquitous. For example, to name just two: energy conversion devices provide electricity to our homes and magnetic recording devices store data in our computers. This chapter provides an introduction to basic magnetism. Starting from the simple attractive (or repelling) force between magnets, we define magnetic field, dipole moment, torque, energy and its equiva- lence to current. Then we will state the Maxwell equations, which describe electromagnetism, or the relationship between electricity and magnetism. A great tutorial is provided by Kittel [1], which may be used to support students studying Chapters 1–4. 1.2 Magnetic forces, poles and fields In the early days, magnetic phenomena were described as analogous to electrical phenomena: like an electric charge, a magnetic pole was considered to be the source of magnetic field and force. The magnetic field was defined through the concept of force exerted on one pole by another. In cgs units, the force is proportional to the strength of the magnetic poles, defined as p p F ¼ 1 2 ; ð1:1Þ r2 where r is the distance between two poles (in units of centimeters) and the unit of force F is the dyne.
    [Show full text]
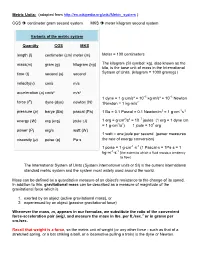
  • Metric Units.Pdf
    Metric Units: (adapted from http://en.wikipedia.org/wiki/Metric_system ) CGS centimeter gram second system MKS meter kilogram second system Variants of the metric system Quantity CGS MKS length (l) centimeter (cm) meter (m) Meter = 100 centimeters mass(m) gram (g) kilogram (kg) The kilogram (SI symbol: kg), also known as the kilo, is the base unit of mass in the International time (t) second (s) second System of Units. (kilogram = 1000 gram(g) ) velocity(v) cm/s m/s acceleration (a) cm/s² m/s² 1 dyne = 1 g·cm/s² = 10−5 kg·m/s² = 10−5 Newton force (F) dyne (dyn) newton (N) 1Newton = 1 kg·m/s2 pressure (p) barye (Ba) pascal (Pa) 1 Ba = 0.1 Pascal = 0.1 Newton/m2 = 1 g·cm-1s-2 2 2 −7 energy (W) erg (erg) joule (J) 1 erg = g·cm /s = 10 joules (1 erg = 1 dyne cm = 1 g·cm2/s2) 1 joule = 107 erg power (P) erg/s watt (W) 1 watt = one joule per second (power measures viscosity (µ) poise (p) Pa·s the rate of energy conversion) 1 poise = 1 g·cm-1·s-1 (1 Pascal·s = 1Pa·s = 1 -1 -1 kg·m ·s (the extent to which a fluid resists a tendency to flow) The International System of Units (System international units or SI) is the current international standard metric system and the system most widely used around the world. Mass can be defined as a quantitative measure of an object's resistance to the change of its speed.
    [Show full text]
  • The SI Metric Systeld of Units and SPE METRIC STANDARD
    The SI Metric SystelD of Units and SPE METRIC STANDARD Society of Petroleum Engineers The SI Metric System of Units and SPE METRIC STANDARD Society of Petroleum Engineers Adopted for use as a voluntary standard by the SPE Board of Directors, June 1982. Contents Preface . ..... .... ......,. ............. .. .... ........ ... .. ... 2 Part 1: SI - The International System of Units . .. .. .. .. .. .. .. .. ... 2 Introduction. .. .. .. .. .. .. .. .. .. .. .. .. 2 SI Units and Unit Symbols. .. .. .. .. .. .. .. .. .. .. .. 2 Application of the Metric System. .. .. .. .. .. .. .. .. .. .. .. .. 3 Rules for Conversion and Rounding. .. .. .. .. .. .. .. .. .. .. .. .. 5 Special Terms and Quantities Involving Mass and Amount of Substance. .. 7 Mental Guides for Using Metric Units. .. .. .. .. .. .. .. .. .. .. .. .. .. 8 Appendix A (Terminology).. .. .. .. .. .. .. .. .. .. .. .. .. 8 Appendix B (SI Units). .. .. .. .. .. .. .. .. .. .. .. .. 9 Appendix C (Style Guide for Metric Usage) ............ ...... ..... .......... 11 Appendix D (General Conversion Factors) ................... ... ........ .. 14 Appendix E (Tables 1.8 and 1.9) ......................................... 20 Part 2: Discussion of Metric Unit Standards. .. .. .. .. .. .. .. .. 21 Introduction.. .. .. .. .. .. .. .. .. .. .. .. 21 Review of Selected Units. .. .. .. .. .. .. .. .. .. .. 22 Unit Standards Under Discussion ......................................... 24 Notes for Table 2.2 .................................................... 25 Notes for Table 2.3 ...................................................
    [Show full text]
  • SI and CGS Units in Electromagnetism
    SI and CGS Units in Electromagnetism Jim Napolitano January 11, 2021 Two divergent systems of units established themselves over the course of the 20th century. One system, known as SI (from the French Le Systeme` International d’Unites),´ is rooted in the laboratory. It gained favor in the engineering community and forms the basis for most undergraduate curricula. The other system, called Gaussian, is aesthetically cleaner and is much favored in the theoretical physics community. We use the Gaussian system in this book, as do most graduate level physics texts on Quantum Mechanics and other subjects. The SI system is also known as MKSA (for meter, kilogram, second, Ampere), and the Gaussian system is some- times called1 CGS (for centimeter, gram, second). For problems in mechanics, the difference is trivial, amounting only to some powers of ten. The difficulty comes when incorporating electromagnetism. As discussed below, SI incorpo- rates a fourth base unit, the Ampere, which implies that charge and other electromagnetic quantities are dimensionally distinct between the SI and Gaussian systems. This one point is the source of all the confusion. In other words, although we can write that a meter is equal to 100 centimeters, the SI unit of charge, called the Coulomb, is not equal to any number of electrostatic units (esu), the Gaussian unit of charge. The two kinds of charges literally have different physical meanings. They should probably have different names, but historically they are both called “charge.” Similar comments apply to electric current, electric and magnetic fields, the electric potential, and so on. This why you see factors like e0 and m0 appear in SI formulas, whereas factors of c are common in Gaussian formulas.
    [Show full text]
  • Units and Conversion Factors
    UNITS AND CONVERSION FACTORS E.J. ROSCHKE PROPULSION DIVISION JET PROPULSION LABORATORY 1 NOTE: Many years ago I was given a copy of this document, prepared in handwriting, some time in the early 1960’s. I did not know the author, E.J. Roschke. I have found it to be such a useful reference that I decided to have an electronic version prepared. Recently, I spoke with Dr. Roschke, now retired from the Jet Propulsion Laboratory to learn of the document’s origin. In the early 1960’s a group of research engineers, largely having backgrounds in mechanical engineering, were engaged in the new field of electric propulsion. They experienced practical annoyances with the mingling of units from mechanical engineering, electrical engineering and physics. That situation motivated Dr. Roschke to assemble this material. Although I have carefully checked the values given here, it is quite possible that some typographical errors remain. I will appreciate learning any corrections that should be made. F.E.C. Culick Mechanical Engineering California Institute of Technology October 2001 2 UNITS AND CONVERSION FACTORS Table of Contents Section Page References 3 I. Decimal Multiples and Submultiples 4 II. Description of Units Mechanical, Electric, Magnetic 4 III. Equivalent Units mksq System 5 IV. Dimensions of esu and emu Electric and Magnetic Quantities 5 V. Dimensions and Units for Physical Quantities — mksq System 6,7 A. Mechanical 6 B. Thermal 7 C. Electric and Magnetic 7 VI. Conversion of mksq Units to Gaussian Units 8 VII. Conversion Factors 8-23 A. Plane Angle 8 B. Solid Angle 8 C.
    [Show full text]