DOCSLIB.ORG

What Are the Basic Properties of the Blood Flow in the Human Body?

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
What Are the Basic Properties of the Blood Flow in the Human Body? Topic of today: Blood flow 1. Design of cardiac array 31545 Medical Imaging systems 2. Basic observations about flow in the human body Conservation of mass Lecture 5: Blood flow in the human body • Conservation of energy • Viscosity • Turbulence • Jørgen Arendt Jensen 3. Pulsating flow and its modeling Department of Health Technology Section for Ultrasound and Biomechanics 4. Pulse propagation and influence of geometric changes in vessels Technical University of Denmark September 13, 2021 5. Questions on Exercise 2 Reading material: JAJ, ch. 3, pages 45-61 1 2 Design an array for cardiac imaging Clean kitchen :) Penetration depth 15 cm and 300 λ Assume distance between ribs is maximum 3 cm The elevation focus should be at 8 cm 1. What is the element pitch? 2. What is the maximum number of elements in the array? 3. What is the lateral resolution at 7 cm? 4. What is the F-number for the elevation focus? 3 4 Human circulatory system Pulmonary circulation through the lungs What are the basic properties of the blood flow Systemic circulation to the organs in the human body? Type Diameter [cm] Arteries 0.2 – 2.4 Arteriole 0.001 – 0.008 Capillaries 0.0004 – 0.0008 Veins 0.6 – 1.5 5 6 Arteries and veins in the body Physical dimensions of arteries and veins Internal Wall Young’s diameter thickness Length modulus Vessel cm cm cm N/m2 105 Ascending aorta 1.0 – 2.4 0.05 – 0.08 5 3 –· 6 Descending aorta 0.8 – 1.8 0.05 – 0.08 20 3 – 6 Abdominal aorta 0.5 – 1.2 0.04 – 0.06 15 9 – 11 Femoral artery 0.2 – 0.8 0.02 – 0.06 10 9 – 12 Carotid artery 0.2 – 0.8 0.02 – 0.04 10 –20 7 – 11 Arteriole 0.001 – 0.008 0.002 0.1 – 0.2 Capillary 0.0004 – 0.0008 0.0001 0.02 – 0.1 Inferior vena cava 0.6 – 1.5 0.01 – 0.02 20 – 40 0.4 – 1.0 Data taken from Caro et al. (1974) 7 8 Velocity parameters in arteries and veins Characteristics of blood flow in humans Peak Mean Reynolds Pulse propaga- velocity velocity number tion velocity Pulsating flow, repetition from 1 to 3 beats/sec Vessel cm/s cm/s (peak) cm/s • Ascending aorta 20 – 290 10 – 40 4500 400 – 600 Not necessarily laminar flow Descending aorta 25 – 250 10 – 40 3400 400 – 600 • Abdominal aorta 50 – 60 8 – 20 1250 700 – 600 Femoral artery 100 – 120 10 – 15 1000 800 – 1030 Short entrance lengths • Carotid artery 50 – 150 20 – 30 600 – 1100 Arteriole 0.5 – 1.0 0.09 Branching Capillary 0.02 – 0.17 0.001 • Inferior vena cava 15 – 40 700 100 – 700 Reynolds numbers usually below 2500, non-turbulent flow • Data taken from Caro et al. (1974) Very complicated flow patterns • Reynolds number: 2Rρ Re = ¯v µ We will start from simple observations and then develop the theory • Indicates turbulence if Re > 2500 (approximately). R - Vessel radius, ρ - Density of blood, µ - Viscosity, ¯v - Mean cross-sectional velocity 9 10 Conservation of mass Stationary flow properties Mass at both ends must be equal: Height h2 Pressure p2 Laminar flow. Particles flow in par- Area A2 Velocity v A1v1ρ1∆t = A2v2ρ2∆t, allel layers with streamlines that do 2 not intersect. Incompressible fluid: ρ1 = ρ2: A Height h 1 1 v = v Pressure p 2 1 No acceleration at a fixed position: 1 A2 Area A1 Velocity v ∂v 1 A2 > A1: Velocity decreases = 0 A2 < A1: Velocity increases ∂t x,y,z Methods for generating a flow: Note, however, that it is possible that v = 0 at changes in geometry Difference in pressure ∇ 6 • Difference in height • 11 12 Relations for a pressure difference Equations: ρ 2 2 Benoulli’s law for conservation of energy p1 p2 = (v v ) − 2 2 − 1 A1 v2 = v1 A2 v2 v2 Combining gives: p + 1 ρ + gh ρ + U = p + 2 ρ + gh ρ + U 1 2 1 1 1 10 2 2 2 2 2 20 2 ρ A1 2 2 p2 = p1 v v ↑ ↑ ↑ ↑ − 2 A 1 − 1 pressure kinetic potential Internal (heat, chemical, friction) 2 ! 2 ρ A1 2 = p1 + 1 v1 2 − A2 ! Assume same height h1 = h2, incompressible fluid ρ1 = ρ2 = ρ, and same internal energy gives Examples: ρ 2 2 p1 p2 = (v2 v1) A < A p < p and v > v − 2 − 2 1 ⇒ 2 1 2 1 A > A p > p and v < v 2 1 ⇒ 2 1 2 1 (Incompressible fluid and same height) 13 14 Viscosity Viscosity properties v Area A F Newtonian fluids have a linear relationHeight between h shear stress and v/d. Shear stress: 2 • Pressure p2 Area A F v 2 0 For non-Newtonian fluids µ is dependentVelocity on v2 shear stress Sxy. d = µ • A d Unit of viscosity is kg/[m s] or centipoise cP (g/[cm s]) µ - Viscosity of fluid • v = 0 Fluid Height h Value1 for water is 1 cP. •Pressure p1 Area A1 Velocity v Shear stress: Blood1 is a Newtonian fluid in major vessels For small fluid element: • ∆F ∆v = µ The viscosity in blood depends on hematocrit (fraction of red blood cell volume), ∆A ∆y • temperature, and pressure. ∆F v+∆v ∆y In the limit: o ∆A v In major vessel the viscosity is usually around 4 cP at 37 and a hematocrit of 45%. y, u ∂vx ∂vy • Sxy = µ + ∂x ∂y ! Viscosity will give rise to parabolic velocity profiles for a laminar, stationary flow. x, v • for a Newtonian fluid. 15 16 Flow models: Stationary parabolic flow Poiseuille flow Pressure difference for a laminar, v(r) Stationary flow: no pul- R • parabolic flow: r sation v o Laminar flow ∆p = Rf Q • Long entrance length • Rf - Viscose resistance Q - Volume flow velocity Profile: 2 r Q = A¯v = v(x, y)dxdy [m3/s] v(r) = 1 v0, − R2! ZZxy Spatial mean velocity over cross section: 8µl = v Rf 4 ¯v = 0 πR 2 l - Distance for pressure drop v0 - Peak velocity at center of vessel, r - Radial position in vessel, - Radius of vessel R - Radius of vessel R 17 18 Example Straight vessel with a diameter of 2 cm, µ = 4 cP rises 20 cm straight up. Mean velocity is 30 cm/s and density is 1060 kg/m3. Giraffe assignment Pressure difference between the ends of the tube? Neglect viscosity, the pressure difference is then given by Bernoulli’s equation What is the change in ρ 2 2 ∆P = (v v ) + ρg(h2 h1). pressure in a Giraffe’s 2 2 − 1 − Straight vessel gives v1 = v2: neck, when it moves it’s head from drink- ∆P = ρg(h2 h1) = 1060 9.82 0.2 = 2082 Pa. − · · Pressure drop due to viscosity is ing to eating leaves in a tree? 8µl 2 8µl 8 0.004 0.2 ∆P = Rf Q = ¯vπR = ¯v = · · 0.3 = 19.2 Pa. πR4 R2 0.012 For a vessel with a diameter of 0.2 cm and a mean velocity of 10 cm/s, the pressure The height of a giraffe drop due to viscosity is is up to 6 m. 8 0.004 0.2 ∆P = · · 0.1 = 640 Pa. 0.0012 There is, thus, a considerable difference in the pressure relationships between a standing person and a person lying flat on a bed. 19 20 Why doesn’t the Giraffe explode? Turbulent flow in tubes Photo of dye injected into a tube with flowing water. The images are taken of the original apparatus as used by Reynold in 1883. Velocity is increasing from the top tube to the bottom one. Image courtesy of Hans Nygaard, Aarhus University. Courtesy of C. Lowe, Manchester School of Engineering. 21 22 Turbulent flow in tubes Disturbed flow in the body Normally non-turbulent flow exists in the body, but it can appear at constrictions, directional changes, and bifurcations: 0.8 Determined by Reynolds number: 0.7 5 2Rρ Re = ¯v 0.6 µ 10 Laminar flow usually found if: 0.5 0.4 Re < 2000 15 Axial distance [mm] 0.3 Turbulent flow found if : 20 0.2 Re > 2500 0.1 Usually non-turbulent flow is found 25 0 in most vessels −5 0 5 [m/s] Lateral distance [mm] Display of velocity direction and magnitude in the carotid bifurcation right after peak systole for a normal volunteer (Courtesy of Jesper Udesen). 23 24 Entrance effects Theoretical velocity profiles 1 0.8 Profiles: p0 0.6 r v(r) = 1 v0 − R 0.4 0.2 p = 32 o 0 p = 8 Development of a steady-state parabolic velocity profile at the entrance to a tube. o Spatial mean velocity −0.2 p = 4 o over cross section: Entrance length: Normalized radial position −0.4 p = 2 o 2 RR ¯v = v0 1 e −0.6 − p + 2 Ze 0 ! ≈ 15 −0.8 −1 Example (aorta): 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 v0 - Peak velocity at center of Velocity [m/s] vessel 0.01 1600 r - Radial position in vessel Ze · 1m Velocity profiles for different values of p0. ≈ 15 ≈ R - Radius of vessel The spatial mean velocity is the same for all profiles. 25 26 Velocity profiles for femoral and carotid artery Modeling pulsatile flow: I Profiles for the femoral artery Profiles for the carotid artery 1 Periodic waveform: 0.5 0 Fourier decomposition of spatial average ve- Velocity [m/s] -0.5 locity: 0 50 100 150 200 250 300 350 Phase [deg.] 1 T Velocity Velocity Vm = ¯v(t) exp( jmωt)dt.
Load more

Recommended publications
  • Cardiovascular System 9
    Chapter Cardiovascular System 9 Learning Outcomes On completion of this chapter, you will be able to: 1. State the description and primary functions of the organs/structures of the car- diovascular system. 2. Explain the circulation of blood through the chambers of the heart. 3. Identify and locate the commonly used sites for taking a pulse. 4. Explain blood pressure. 5. Recognize terminology included in the ICD-10-CM. 6. Analyze, build, spell, and pronounce medical words. 7. Comprehend the drugs highlighted in this chapter. 8. Describe diagnostic and laboratory tests related to the cardiovascular system. 9. Identify and define selected abbreviations. 10. Apply your acquired knowledge of medical terms by successfully completing the Practical Application exercise. 255 Anatomy and Physiology The cardiovascular (CV) system, also called the circulatory system, circulates blood to all parts of the body by the action of the heart. This process provides the body’s cells with oxygen and nutritive ele- ments and removes waste materials and carbon dioxide. The heart, a muscular pump, is the central organ of the system. It beats approximately 100,000 times each day, pumping roughly 8,000 liters of blood, enough to fill about 8,500 quart-sized milk cartons. Arteries, veins, and capillaries comprise the network of vessels that transport blood (fluid consisting of blood cells and plasma) throughout the body. Blood flows through the heart, to the lungs, back to the heart, and on to the various body parts. Table 9.1 provides an at-a-glance look at the cardiovascular system. Figure 9.1 shows a schematic overview of the cardiovascular system.
    [Show full text]
  • Blood and Lymph Vascular Systems
    BLOOD AND LYMPH VASCULAR SYSTEMS BLOOD TRANSFUSIONS Objectives Functions of vessels Layers in vascular walls Classification of vessels Components of vascular walls Control of blood flow in microvasculature Variation in microvasculature Blood barriers Lymphatic system Introduction Multicellular Organisms Need 3 Mechanisms --------------------------------------------------------------- 1. Distribute oxygen, nutrients, and hormones CARDIOVASCULAR SYSTEM 2. Collect waste 3. Transport waste to excretory organs CARDIOVASCULAR SYSTEM Cardiovascular System Component function Heart - Produce blood pressure (systole) Elastic arteries - Conduct blood and maintain pressure during diastole Muscular arteries - Distribute blood, maintain pressure Arterioles - Peripheral resistance and distribute blood Capillaries - Exchange nutrients and waste Venules - Collect blood from capillaries (Edema) Veins - Transmit blood to large veins Reservoir Larger veins - receive lymph and return blood to Heart, blood reservoir Cardiovascular System Heart produces blood pressure (systole) ARTERIOLES – PERIPHERAL RESISTANCE Vessels are structurally adapted to physical and metabolic requirements. Vessels are structurally adapted to physical and metabolic requirements. Cardiovascular System Elastic arteries- conduct blood and maintain pressure during diastole Cardiovascular System Muscular Arteries - distribute blood, maintain pressure Arterioles - peripheral resistance and distribute blood Capillaries - exchange nutrients and waste Venules - collect blood from capillaries
    [Show full text]
  • Why Is Plasma Renin Activity Lower in Populations of African Origin?
    Journal of Human Hypertension (2001) 15, 17–25 2001 Macmillan Publishers Ltd All rights reserved 0950-9240/01 $15.00 www.nature.com/jhh REVIEW ARTICLE Why is plasma renin activity lower in populations of African origin? GA Sagnella Blood Pressure Unit, St George’s Hospital Medical School, Cranmer Terrace, London SW17 ORE, UK Plasma renin activity is significantly lower in black the molecular level suggests that the lower PRA may people compared with whites independent of age and arise from gene variation in the renal epithelial sodium blood pressure status. The lower PRA appears to be due channel. The functional significance of the lower PRA in to a reduction in the rate of secretion of renin but the relation to the different pattern of cardiovascular and exact mechanistic events underlying such differences in renal disease between blacks and whites remains renin release between blacks and whites are still not unclear. Moreover, direct investigations of pre-treat- fully understood. Nevertheless, given the paramount ment renin status in hypertensive blacks in relation to importance of the renin-angiotensin system in the con- blood pressure response have demonstrated that the trol of sodium balance, a most likely explanation is that pre-treatment PRA is not a good index of subsequent the lower renin is a consequence of differences in renal blood pressure response to pharmacological treatment. sodium handling between blacks and whites. The lower Nevertheless, the blood pressure reduction to short PRA does not reflect differences in dietary sodium term sodium restriction is greater in blacks compared intake but the evidence available suggests that the low with whites and, in the black subjects, the greater PRA could be part of the corrective mechanisms reduction in blood pressure to sodium restriction designed to maintain sodium balance in the presence appears to be related, at least in part, to the decreased of an increased tendency for sodium retention in black responsiveness of the renin-angiotensin system.
    [Show full text]
  • Thoracic Aorta
    GUIDELINES AND STANDARDS Multimodality Imaging of Diseases of the Thoracic Aorta in Adults: From the American Society of Echocardiography and the European Association of Cardiovascular Imaging Endorsed by the Society of Cardiovascular Computed Tomography and Society for Cardiovascular Magnetic Resonance Steven A. Goldstein, MD, Co-Chair, Arturo Evangelista, MD, FESC, Co-Chair, Suhny Abbara, MD, Andrew Arai, MD, Federico M. Asch, MD, FASE, Luigi P. Badano, MD, PhD, FESC, Michael A. Bolen, MD, Heidi M. Connolly, MD, Hug Cuellar-Calabria, MD, Martin Czerny, MD, Richard B. Devereux, MD, Raimund A. Erbel, MD, FASE, FESC, Rossella Fattori, MD, Eric M. Isselbacher, MD, Joseph M. Lindsay, MD, Marti McCulloch, MBA, RDCS, FASE, Hector I. Michelena, MD, FASE, Christoph A. Nienaber, MD, FESC, Jae K. Oh, MD, FASE, Mauro Pepi, MD, FESC, Allen J. Taylor, MD, Jonathan W. Weinsaft, MD, Jose Luis Zamorano, MD, FESC, FASE, Contributing Editors: Harry Dietz, MD, Kim Eagle, MD, John Elefteriades, MD, Guillaume Jondeau, MD, PhD, FESC, Herve Rousseau, MD, PhD, and Marc Schepens, MD, Washington, District of Columbia; Barcelona and Madrid, Spain; Dallas and Houston, Texas; Bethesda and Baltimore, Maryland; Padua, Pesaro, and Milan, Italy; Cleveland, Ohio; Rochester, Minnesota; Zurich, Switzerland; New York, New York; Essen and Rostock, Germany; Boston, Massachusetts; Ann Arbor, Michigan; New Haven, Connecticut; Paris and Toulouse, France; and Brugge, Belgium (J Am Soc Echocardiogr 2015;28:119-82.) TABLE OF CONTENTS Preamble 121 B. How to Measure the Aorta 124 I. Anatomy and Physiology of the Aorta 121 1. Interface, Definitions, and Timing of Aortic Measure- A. The Normal Aorta and Reference Values 121 ments 124 1.
    [Show full text]
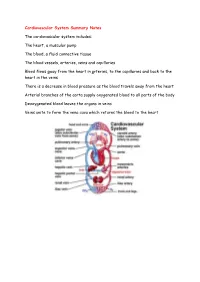
  • Cardiovascular System Summary Notes the Cardiovascular System
    Cardiovascular System Summary Notes The cardiovascular system includes: The heart, a muscular pump The blood, a fluid connective tissue The blood vessels, arteries, veins and capillaries Blood flows away from the heart in arteries, to the capillaries and back to the heart in the veins There is a decrease in blood pressure as the blood travels away from the heart Arterial branches of the aorta supply oxygenated blood to all parts of the body Deoxygenated blood leaves the organs in veins Veins unite to form the vena cava which returns the blood to the heart Pulmonary System This is the route by which blood is circulated from the heart to the lungs and back to the heart again The pulmonary system is exceptional in that the pulmonary artery carries deoxygenated blood and the pulmonary vein carries oxygenated blood Hepatic Portal Vein There is another exception in the circulatory system – the hepatic portal vein Veins normally carry blood from an organ back to the heart The hepatic portal vein carries blood from the capillary bed of the intestine to the capillary bed of the liver As a result, the liver has three blood vessels associated with it Arteries and Veins The central cavity of a blood vessel is called the lumen The lumen is lined with a thin layer of cells called the endothelium The composition of the vessel wall surrounding the endothelium is different in arteries, veins and capillaries Arteries carry blood away from the heart Arteries have a thick middle layer of smooth muscle They have an inner and outer layer of elastic fibres Elastic
    [Show full text]
  • Blood Vessels
    BLOOD VESSELS Blood vessels are how blood travels through the body. Whole blood is a fluid made up of red blood cells (erythrocytes), white blood cells (leukocytes), platelets (thrombocytes), and plasma. It supplies the body with oxygen. SUPERIOR AORTA (AORTIC ARCH) VEINS & VENA CAVA ARTERIES There are two basic types of blood vessels: veins and arteries. Veins carry blood back to the heart and arteries carry blood from the heart out to the rest of the body. Factoid! The smallest blood vessel is five micrometers wide. To put into perspective how small that is, a strand of hair is 17 micrometers wide! 2 BASIC (ARTERY) BLOOD VESSEL TUNICA EXTERNA TUNICA MEDIA (ELASTIC MEMBRANE) STRUCTURE TUNICA MEDIA (SMOOTH MUSCLE) Blood vessels have walls composed of TUNICA INTIMA three layers. (SUBENDOTHELIAL LAYER) The tunica externa is the outermost layer, primarily composed of stretchy collagen fibers. It also contains nerves. The tunica media is the middle layer. It contains smooth muscle and elastic fiber. TUNICA INTIMA (ELASTIC The tunica intima is the innermost layer. MEMBRANE) It contains endothelial cells, which TUNICA INTIMA manage substances passing in and out (ENDOTHELIUM) of the bloodstream. 3 VEINS Blood carries CO2 and waste into venules (super tiny veins). The venules empty into larger veins and these eventually empty into the heart. The walls of veins are not as thick as those of arteries. Some veins have flaps of tissue called valves in order to prevent backflow. Factoid! Valves are found mainly in veins of the limbs where gravity and blood pressure VALVE combine to make venous return more 4 difficult.
    [Show full text]
  • Fetal Descending Aorta/Umbilical Artery Flow Velocity Ratio in Normal Pregnancy at 36-40 Weeks of Gestational Age Riyadh W Alessawi1
    American Journal of BioMedicine AJBM 2015; 3(10):674 - 685 doi:10.18081/2333-5106/015-10/674-685 Fetal descending aorta/umbilical artery flow velocity ratio in normal pregnancy at 36-40 Weeks of gestational age Riyadh W Alessawi1 Abstract Doppler velocimetry studies of placental and aortic circulation have gained a wide popularity as it can provide important information regarding fetal well-being and could be used to identify fetuses at risk of morbidity and mortality, thus providing an opportunity to improve fetal outcomes. Prospective longitudinal study conducted through the period from September 2011–July 2012, 125 women with normal pregnancy and uncomplicated fetal outcomes were recruited and subjected to Doppler velocimetry at different gestational ages, from 36 to 40 weeks. Of those, 15 women did not fulfill the protocol inclusion criteria and were not included. In the remaining 110 participants a follow up study of Fetal Doppler velocimetry of Ao and UA was performed at 36 – 40 weeks of gestation. Ao/UA RI: 1.48±0.26, 1.33±0.25, 1.37± 0.20, 1.28±0.07 and 1.39±0.45 respectively and the 95% confidence interval of the mean for five weeks 1.13-1.63. Ao/UA PI: 2.83±2.6, 1.94±0.82, 2.08±0.53, 1.81± 0.12 and 3.28±2.24 respectively. Ao/UA S/D: 2.14±0.72, 2.15±1.14, 1.75±0.61, 2.52±0.18 and 2.26±0.95. The data concluded that a nomogram of descending aorto-placental ratio Ao/UA, S/D, PI and RI of Iraqi obstetric population was established.
    [Show full text]
  • SGLT2 Inhibition and Potential Renal Protection
    The knowns and unknowns of SGLT2 inhibition in CKD Paola Fioretto, MD Padua, Italy June 14, 2019 - Budapest, Hungary SGLT2 inhibition in CKD: Discussing the key questions and evidence Budapest, june 14 2019 The knowns and unknowns of SGLT2 inhibition in CKD Paola Fioretto Department of Medicine University of Padova, Italy 180 g of glucose filtered Glomerulus Proximal tubule Distal tubule Collecting duct each day S1 S2 Glucose filtration S3 SGLT2 SGLT1 90% 10% Glucose reabsorption Loop of Henle Up to ~ 90% of glucose ~ 10% of glucose Minimal is reabsorbed is reabsorbed glucose from the S1/S2 segments from the S3 segment excretion Possible mechanisms responsible for cardiovascular and renal protection with SGLT2 inhibition SGLT2 inhibition Glycosuria Natriuresis ↓Blood ↓Plasma Negative caloric balance ↑Uricosuria pressure ↑Tubuloglomerular volume feedback ↓Myocardial ↓HbA1c ↓ Afferent stretch ↓ ↓Plasma uric ↓Arterial ↓ arteriole acid stiffness ↑ constriction ↓Total body fat mass ↓Inflammation ↓Glucose toxicity ↓Epicardial fat ↓Intraglomerular hypertension ↓Ventricular ↓Hyperfiltration arrhythmias ↓Atherosclerosis Activation of ACE2 – Ang1/7 ↑Cardiac contractility ↓Inflammation No sympathetic nervous system activation ↓Fibrosis Cardiac and renal protection Heerspink HJ et al, Circulation 2016 Tonneijck et al, J Am Soc Nephrol 2017 Diabetic nephron Diabetic nephron with SGLT2 i Effects of SGLT2 i on afferent arteriole tone: in vivo studies with multiphoton microscope imaging techniques Kidokoro K et al, Circulation 2019 Effects of SGLT2 i
    [Show full text]
  • Inferior Phrenic Artery, Variations in Origin and Clinical Implications – a Case Study
    IOSR Journal of Dental and Medical Sciences (IOSR-JDMS) E-ISSN: 2279-0853, p-ISSN: 2279-0861. Volume 7, Issue 6 (Mar.- Apr. 2013), PP 46-48 www.iosrjournals.org Inferior Phrenic Artery, Variations in Origin and Clinical Implications – A Case Study 1 2 3 Dr.Anupama D, Dr.R.Lakshmi Prabha Subhash .Dr. B.S Suresh Assistant Professor. Dept. Of Anatomy, SSMC. Tumkur.Karnataka.India Professor & HOD. Dept. Of Anatomy, SSMC. Tumkur.Karnataka.India Associate professor.Dept. Of Anatomy, SSMC. Tumkur.Karnataka.India Abstract:Variations in the branching pattern of abdominal aorta are quite common, knowledge of which is required to avoid complications during surgical interventions involving the posterior abdominal wall. Inferior Phrenic Arteries, the lateral aortic branches usually arise from Abdominal Aorta ,just above the level of celiac trunk. Occasionally they arise from a common aortic origin with celiac trunk, or from the celiac trunk itself or from the renal artery. This study describes the anomalous origin of this lateral or para aortic branches in the light of embryological and surgical basis. Knowledge of such variations has important clinical significance in abdominal operations like renal transplantation, laparoscopic surgery, and radiological procedures in the upper abdomen or invasive arterial procedures . Keywords: Abdominal Aorta, Celiac Trunk(Ct), Diaphragm, Inferior Phrenic Artery (Ipa), Retro Peritoneal, Renal Artery(Ra). I. Introduction The abdominal aorta begins from the level of 12th thoracic vertebra after passing through the Osseo aponeurotic hiatus of diaphragm. It courses downwards with Inferior vena cava to its right and terminates at the level of 4th lumbar vertebra by dividing in to two terminal branches.
    [Show full text]
  • Superior Mesenteric Artery and Nutcracker Syndromes in a Healthy 14-Year-Old Girl Requiring Surgical Intervention After Failed Conservative Management
    ISSN 2377-8369 GASTRO Open Journal Case Report Superior Mesenteric Artery and Nutcracker Syndromes in a Healthy 14-Year-Old Girl Requiring Surgical Intervention after Failed Conservative Management David Wood, MRCPCH, MSc1; Andrew Fagbemi, FRCPCH2; Loveday Jago, MRCPCH2; Dalia Belsha, MRCPCH2; Nick Lansdale, FRCS, PhD3; Ahmed Kadir, FRCPCH, MSc2* 1Paediatric Registrar, Royal Manchester Children’s Hospital, Manchester, UK 2Paediatric Gastroenterology Consultant, Royal Manchester Children’s Hospital, Manchester, UK 3Paediatric Surgeon, Royal Manchester Children’s Hospital, Manchester, UK *Corresponding author Ahmed Kadir, FRCPCH, MSc Paediatric Gastroenterology Consultant, Royal Manchester Children’s Hospital, Manchester, UK; Phone. 07709732356; E-mail: [email protected] Article information Received: January 30th, 2020; Revised: February 17th, 2020; Accepted: February 24th, 2020; Published: February 28th, 2020 Cite this article Wood D, Fagbemi A, Jago L, Belsha D, Lansdale N, Kadir A. Superior mesenteric artery and nutcracker syndromes in a healthy 14-year-old girl requiring surgical intervention after failed conservative management. Gastro Open J. 2020; 5(1): 1-3. doi: 10.17140/GOJ-5-132 ABSTRACT This case report presents the diagnosis of superior mesenteric artery and nutcracker syndromes in a previously fit and well 14-year- old girl. Although these two entities usually occur in isolation, despite their related aetiology, our patient was a rare example of their occurrence together. In this case the duodenal compression of superior mesenteric artery syndrome caused intractable vom- iting leading to weight loss, and her nutcracker syndrome caused severe left-sided abdominal pain and microscopic haematuria without renal compromise. Management of the superior mesenteric artery syndrome can be conservative by increasing the weight of the child which leads to improvement of retroperitoneal fat and hence the angle of the artery.
    [Show full text]
  • Normal and Variant Origin and Branching Pattern of Inferior Phrenic Arteries and Their Clinical Implications: a Cadaveric Study
    International Journal of Research in Medical Sciences Thamke S et al. Int J Res Med Sci. 2015 Jan;3(1):282-286 www.msjonline.org pISSN 2320-6071 | eISSN 2320-6012 DOI: 10.5455/2320-6012.ijrms20150151 Research Article Normal and variant origin and branching pattern of inferior phrenic arteries and their clinical implications: a cadaveric study Swati Thamke1*, Pooja Rani2 1Department of Anatomy, UCMS & GTB Hospital, Delhi, India 2Department of Anatomy, PGIMS, Rohtak, Haryana, India Received: 6 December 2014 Accepted: 18 December 2014 *Correspondence: Dr. Swati Thamke, E-mail: [email protected] Copyright: © the author(s), publisher and licensee Medip Academy. This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT Background: Inferior phrenic arteries, which constitute the chief arterial supply to the diaphragm, are generally the branches of abdominal aorta, however, variations in their mode of origin is not uncommon. Very less information is available regarding the functional anatomy of the inferior phrenic artery in anatomy textbooks. Methods: The present study was conducted utilizing 36 formaline-fixed cadavers between 22 years to 80 years over a period of 5 years. The frequency and anatomical pattern of the origin of the right and left inferior phrenic arteries were studied. Results: On the right side, the inferior phrenic artery arose independently from abdominal aorta in 94.4% cases and on the left side in 97.2% cases.Other sources of origin were seen in 5.55% cases.
    [Show full text]
  • Blood Vessels and Circulation
    19 Blood Vessels and Circulation Lecture Presentation by Lori Garrett © 2018 Pearson Education, Inc. Section 1: Functional Anatomy of Blood Vessels Learning Outcomes 19.1 Distinguish between the pulmonary and systemic circuits, and identify afferent and efferent blood vessels. 19.2 Distinguish among the types of blood vessels on the basis of their structure and function. 19.3 Describe the structures of capillaries and their functions in the exchange of dissolved materials between blood and interstitial fluid. 19.4 Describe the venous system, and indicate the distribution of blood within the cardiovascular system. © 2018 Pearson Education, Inc. Module 19.1: The heart pumps blood, in sequence, through the arteries, capillaries, and veins of the pulmonary and systemic circuits Blood vessels . Blood vessels conduct blood between the heart and peripheral tissues . Arteries (carry blood away from the heart) • Also called efferent vessels . Veins (carry blood to the heart) • Also called afferent vessels . Capillaries (exchange substances between blood and tissues) • Interconnect smallest arteries and smallest veins © 2018 Pearson Education, Inc. Module 19.1: Blood vessels and circuits Two circuits 1. Pulmonary circuit • To and from gas exchange surfaces in the lungs 2. Systemic circuit • To and from rest of body © 2018 Pearson Education, Inc. Module 19.1: Blood vessels and circuits Circulation pathway through circuits 1. Right atrium (entry chamber) • Collects blood from systemic circuit • To right ventricle to pulmonary circuit 2. Pulmonary circuit • Pulmonary arteries to pulmonary capillaries to pulmonary veins © 2018 Pearson Education, Inc. Module 19.1: Blood vessels and circuits Circulation pathway through circuits (continued) 3. Left atrium • Receives blood from pulmonary circuit • To left ventricle to systemic circuit 4.
    [Show full text]