DOCSLIB.ORG

Discrete Symmetries

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Discrete Symmetries Discrete Symmetries by Prof.dr Ing. J. F. J. van den Brand Vrije Universiteit Amsterdam, The Netherlands www.nikhef.nl/ jo 1 2 Contents 1 INTRODUCTION 5 2 Symmetries 7 2.1SymmetriesinQuantumMechanics...................... 7 2.2ContinuousSymmetryTransformations.................... 9 2.2.1 ConservationofMomentum...................... 9 2.2.2 ChargeConservation.......................... 10 2.2.3 LocalGaugeSymmetries........................ 11 2.2.4 ConservationofBaryonNumber.................... 14 2.2.5 ConservationofLeptonNumber.................... 15 2.3DiscreteSymmetryTransformations...................... 19 2.3.1 Parity or Symmetry under Spatial Reflections . ......... 19 2.3.2 Parity Violation in β-decay...................... 20 2.3.3 HelicityofLeptons........................... 22 2.3.4 ConservationofParityintheStrongInteraction........... 24 2.4ChargeSymmetry................................ 26 2.4.1 Particles and Antiparticles, -Theorem.............. 26 2.4.2 ChargeSymmetryoftheStrongInteraction.............CPT 30 2.5 Invariance under Time Reversal ........................ 31 2.5.1 PrincipleofDetailedBalance..................... 34 2.5.2 ElectricDipoleMomentoftheNeutron................ 34 2.5.3 Triple Correlations in β-Decay..................... 36 3SU(2) U(1) Symmetry or Standard Model 37 3.1NotesonFieldTheory.............................× 37 3.1.1 DiracEquation............................. 38 3.1.2 QuantumFields............................. 38 3.2ElectroweakInteractionintheStandardModel............... 42 3.2.1 ElectroweakBosons........................... 42 3.2.2 FermionsintheStandardModel.................... 47 4 Quark Mixing 53 4.1Introduction................................... 53 4.2CabibboFormalism............................... 54 4.3GIMScheme................................... 54 4.3.1 SummaryofQuarkMixinginTwoGenerations........... 55 4.4TheCabibbo-Kobayashi-MaskawaMixingMatrix.............. 57 5 The neutral Kaon system 63 5.1ParticleMixingfortheNeutralK-Mesons.................. 63 5.2MassandDecayMatrices........................... 67 5.3Regeneration.................................. 70 5.4 CP Violation with Neutral Kaons . .................... 72 5.5IsospinAnalysis................................. 76 5.6CPViolationinSemileptonicDecay...................... 80 5.7 CPT Theorem and the Neutral Kaon System ................. 81 3 5.7.1 GeneralizedFormalism......................... 81 5.7.2 CPSymmetry.............................. 82 5.7.3 TimeReversalInvarianceandCPTInvariance............ 83 5.7.4 IsospinAmplitudes........................... 83 5.8ParticleMixingandtheStandardModel................... 84 6 The B-meson system 89 6.1CPViolationintheStandardModel..................... 89 6.1.1 CPViolationinneutralBdecays................... 91 6.1.2 MeasurementofRelevantParameters................. 95 6.1.3 MeasurementoftheAnglesoftheUnitarityTriangle........100 7 Status of Experiments 105 7.1TheLHCbExperimentatCERN.......................105 8 PROBLEMS 107 8.1TimeReversal..................................107 8.2ChargeConjugation...............................107 8.3 -Theorem..................................107 8.4CabibboAngle.................................107CPT 8.5UnitaryMatrix.................................107 8.6QuarkPhases..................................108 8.7ExploitingUnitarity..............................108 8.8D-mesonDecay.................................108 8.9MassandDecayMatrix............................108 8.10 Kaon Intensities . ...............................108 8.11OpticalTheorem................................109 8.12 Neutral Kaon States in Matter .........................109 8.13RegenerationParameter............................109 8.14IsospinAnalysis.................................109 9 APPENDIX B: SOLUTIONS 111 9.1Cabibboangle..................................111 9.2UnitaryMatrix.................................111 9.3QuarkPhases..................................111 9.4ExploitingUnitarity..............................112 9.5D-mesonDecay.................................112 9.6MassandDecayMatrix............................113 9.7 Kaon Intensities . ...............................114 9.8OpticalTheorem................................115 9.9 Neutral Kaon States in Matter .........................116 9.10RegenerationParameter............................117 9.11IsospinAnalysis.................................117 4 1 INTRODUCTION Symmetries and conservation laws play a fundamental role in physics. The invariance of a system under a continuous symmetry transformation leads to a conservation law by Noethers’ theorem. For example, the invariance under space and time translations results in momentum and energy conservation. Besides these continuous symmetries one has discrete symmetries that play an important role. Particularly, three such discrete symmetries are a topic of interest in modern particle physics. The parity transformation performs a reflection of the space coordinates at the origin (~r ~r). Position and momentumP change sign, while spin is unaffected. The charge conjugation→− operator transforms a particle into its antiparticle and vice versa. All intrinsic ‘charges’ change sign,C but motion and spin are left unchanged. Time reversal operates on the time coordinate. Now also spin changes sign, like momentum and velocity.T Composed symmetries, such as and , can also be considered. It was long thought that was an exact symmetry inCP nature.CPT In 1964 -violation was discovered in the neutral kaonCP system by Christensen, Cronin, Fitch andCP Turlay. A few years later Kobayashi and Maskawa demonstrated that a third quark generation could accommodate violation in the Standard Model by a complex phase in the CKM matrix. Since then,CP however, (or ) violation has not been observed in any other system and we do not understandCP its mechanismsT and rare processes. The discovery of the b-quark in 1977 opened a new possibility to test the Standard Model in B-mesons studies. This might answer unresolved questions in the Standard Model or lead to new physics. With experiments that study B-meson decay one mainly addresses the following questions: Is the phase of the CKM-matrix the only source of -violation? • CP What are the exact values of the components of the CKM-matrix? • Is there new physics in the quark region? • This introductory course is structured as follows. In chapter 2, an introduction to quark mixing is given. In our discussions we will follow a historic route. The present status of violation in the kaon system is discussed in chapter 3. Chapter 4 gives a brief overviewCP of violation in the neutral B-meson system. The merit of various experiments for theCP study of violation in the B sector is discussed in chapter 5. The LHCb experiment is describedCP in somewhat more detail. Appendix A provides a set of exercises. Solutions are presented in appendix B. 5 6 2 Symmetries 2.1 Symmetries in Quantum Mechanics The concept of symmetries and their associated conservation laws has proven extraordi- nary useful in particle physics. From classical physics we know, for example, that the demand that laws need to be invariant under translation in time, leads to conservation of energy. In addition, one has that invariance with respect to spatial rotations leads to conservation of angular momentum. While the conservation laws for energy, momentum and angular momenta are always strictly valid, we know that other symmetries are bro- ken in certain interactions. It was for example quite a surprise for physicists when it was demonstrated that mirror symmetry is violated in the weak interaction (and only in this interaction!); even maximally violated. Furthermore, we presently do not understand why this is the case, or why certain other symmetries ( , ) are only ‘slightly violated’. CP T Here, we first want to summarize the quantum mechanical basis, which we will need for our discussion of the various phenomena. A system is described by a wave function, ψ. A physical observable is represented by a quantum mechanical operator, O,whose expectation values are given by the eigenvalues of this operator. The eigenvalues corre- spond to the results of measurements, and the expectation value of O in the state ψa is defined as1 <O>= ψa∗OψadV. (3) Z Since the expectation values can be determined experimentally, they need to be real quantities, and consequently O needs to be hermitian. When O is an operator, then its hermitian conjugate operator O† is defined as (Oψ)∗φdV = ψ∗O†φdV, (4) Z Z and the operator O is called hermitian when one has O† = O. The time dependence of the wave function, ψ, is given by the Schr¨odinger equation, ∂ψ ih¯ = Hψ. (5) ∂t In case the hamiltonian H is real, one also has ∂ψ∗ ih¯ =(Hψ)∗ = ψ∗H. (6) − ∂t 1When we consider two states, one can write in analog fashion Oba = b∗O adV; (1) Z and Oba is called the transition matrix element between the states a en b. The expectation value of O in state a is the diagonal element of Oba for b = a, <O>= Oaa: (2) The non-diagonal elements do not directly correspond to classical observables. However, the transitions between states a and b are related to Oba. 7 For the time dependence of an observable, O, we then find ∂ ∂ ∂t <O> = ∂t ψ∗OψdV R ∂ψ∗ ∂ψ = ∂t Oψ + ψ∗O ∂t dV (7) R i = ψ∗(HO OH)ψdV. ¯h − R Thus, we conclude that <O>does not chance, and corresponds to a constant of motion, in case the commutator [H, O]vanishes, [H, O] HO OH =0. (8) ≡ − Consequently, a wave function can be found, that is simultaenously an eigenfunction of O and of H, Hψ = Eψ and Oψ = oψ, (9)
Load more

Recommended publications
  • The Moedal Experiment at the LHC. Searching Beyond the Standard
    126 EPJ Web of Conferences , 02024 (2016) DOI: 10.1051/epjconf/201612602024 ICNFP 2015 The MoEDAL experiment at the LHC Searching beyond the standard model James L. Pinfold (for the MoEDAL Collaboration)1,a 1 University of Alberta, Physics Department, Edmonton, Alberta T6G 0V1, Canada Abstract. MoEDAL is a pioneering experiment designed to search for highly ionizing avatars of new physics such as magnetic monopoles or massive (pseudo-)stable charged particles. Its groundbreaking physics program defines a number of scenarios that yield potentially revolutionary insights into such foundational questions as: are there extra dimensions or new symmetries; what is the mechanism for the generation of mass; does magnetic charge exist; what is the nature of dark matter; and, how did the big-bang develop. MoEDAL’s purpose is to meet such far-reaching challenges at the frontier of the field. The innovative MoEDAL detector employs unconventional methodologies tuned to the prospect of discovery physics. The largely passive MoEDAL detector, deployed at Point 8 on the LHC ring, has a dual nature. First, it acts like a giant camera, comprised of nuclear track detectors - analyzed offline by ultra fast scanning microscopes - sensitive only to new physics. Second, it is uniquely able to trap the particle messengers of physics beyond the Standard Model for further study. MoEDAL’s radiation environment is monitored by a state-of-the-art real-time TimePix pixel detector array. A new MoEDAL sub-detector to extend MoEDAL’s reach to millicharged, minimally ionizing, particles (MMIPs) is under study Finally we shall describe the next step for MoEDAL called Cosmic MoEDAL, where we define a very large high altitude array to take the search for highly ionizing avatars of new physics to higher masses that are available from the cosmos.
    [Show full text]
  • CHAPTER 12: the Atomic Nucleus
    CHAPTER 12 The Atomic Nucleus ◼ 12.1 Discovery of the Neutron ◼ 12.2 Nuclear Properties ◼ 12.3 The Deuteron ◼ 12.4 Nuclear Forces ◼ 12.5 Nuclear Stability ◼ 12.6 Radioactive Decay ◼ 12.7 Alpha, Beta, and Gamma Decay ◼ 12.8 Radioactive Nuclides Structure of matter Dark matter and dark energy are the yin and yang of the cosmos. Dark matter produces an attractive force (gravity), while dark energy produces a repulsive force (antigravity). ... Astronomers know dark matter exists because visible matter doesn't have enough gravitational muster to hold galaxies together. Hierarchy of forces ◼ Sta Standard Model tries to unify the forces into one force Ernest Rutherford “Father of the Nucleus” Story so far: Unification Faraday Glashow,Weinberg,Salam Georgi,Glashow Green,Schwarz Witten 1831 1967 1974 1984 1995 Electricity } } } Electromagnetic force } } } Magnetism} } Electro-weak force } } } Weak nuclear force} } Grand unified force } } } 5 Different } Strong nuclear force} } D=10 String } M-theory ? } Theories } Gravitational force} +branes in D=11 Page 6 © Imperial College London Discovery of the Neutron 3) Nuclear magnetic moment: The magnetic moment of an electron is over 1000 times larger than that of a proton. The measured nuclear magnetic moments are on the same order of magnitude as the proton’s, so an electron is not a part of the nucleus. ◼ In 1930 the German physicists Bothe and Becker used a radioactive polonium source that emitted α particles. When these α particles bombarded beryllium, the radiation penetrated several centimeters of lead. The neutrons collide elastically with the protons of the paraffin thereby producing the5.7 MeV protons Discovery of the Neutron ◼ Photons are called gamma rays when they originate from the nucleus.
    [Show full text]
  • Non-Collider Searches for Stable Massive Particles
    Non-collider searches for stable massive particles S. Burdina, M. Fairbairnb, P. Mermodc,, D. Milsteadd, J. Pinfolde, T. Sloanf, W. Taylorg aDepartment of Physics, University of Liverpool, Liverpool L69 7ZE, UK bDepartment of Physics, King's College London, London WC2R 2LS, UK cParticle Physics department, University of Geneva, 1211 Geneva 4, Switzerland dDepartment of Physics, Stockholm University, 106 91 Stockholm, Sweden ePhysics Department, University of Alberta, Edmonton, Alberta, Canada T6G 0V1 fDepartment of Physics, Lancaster University, Lancaster LA1 4YB, UK gDepartment of Physics and Astronomy, York University, Toronto, ON, Canada M3J 1P3 Abstract The theoretical motivation for exotic stable massive particles (SMPs) and the results of SMP searches at non-collider facilities are reviewed. SMPs are defined such that they would be suffi- ciently long-lived so as to still exist in the cosmos either as Big Bang relics or secondary collision products, and sufficiently massive such that they are typically beyond the reach of any conceiv- able accelerator-based experiment. The discovery of SMPs would address a number of important questions in modern physics, such as the origin and composition of dark matter and the unifi- cation of the fundamental forces. This review outlines the scenarios predicting SMPs and the techniques used at non-collider experiments to look for SMPs in cosmic rays and bound in mat- ter. The limits so far obtained on the fluxes and matter densities of SMPs which possess various detection-relevant properties such as electric and magnetic charge are given. Contents 1 Introduction 4 2 Theory and cosmology of various kinds of SMPs 4 2.1 New particle states (elementary or composite) .
    [Show full text]
  • Lesson 6.3 You Experience Is Related to Your Location on the Globe
    Key Objectives 6.3.1 DESCRIBE trends among elements for 6.3 Periodic Trends atomic size. 6.3.2 EXPLAIN how ions form. 6.3.3 DESCRIBE trends for first ionization energy, ionic size, and electronegativity. CHEMISTRY & YOUY Additional Resources Q: How are trends in the weather similar to trends in the properties of elements? Although the weather changes from day to day. The weather Reading and Study Workbook, Lesson 6.3 you experience is related to your location on the globe. For example, LESSON 6.3 Available Online or on Digital Media: Florida has an average temperature that is higher than Minnesota’s. Similarly, a rain forest receives more rain than a desert. These differ- • Teaching Resources, Lesson 6.3 Review ences are attributable to trends in the weather. In this lesson, you will • Small-Scale Chemistry Laboratory Manual, Lab 9 learn how a property such as atomic size is related to the location of an element in the periodic table. Key Questions Trends in Atomic Size What are the trends among the What are the trends among the elements for atomic size? ? elements for atomic size One way to think about atomic size is to look at the units that form How do ions form? when atoms of the same element are joined to one another. These What are the trends among the units are called molecules. Figure 6.14 shows models of molecules Engage elements for first ionization energy, (molecular models) for seven nonmetals. Because the atoms in each ionic size, and electronegativity? molecule are identical, the distance between the nuclei of these atoms CHEMISTRY YOUYOY U Have students read the can be used to estimate the size of the atoms.
    [Show full text]
  • Search for Supersymmetry Events with Two Same-Sign Leptons
    Search for supersymmetry events with two same-sign leptons Dissertation der Fakult¨atf¨urPhysik der Ludwig-Maximilians-Universit¨atM¨unchen vorgelegt von Christian Kummer geboren in M¨unchen M¨unchen, im Januar 2010 1. Gutachter: Prof. Dr. Dorothee Schaile 2. Gutachter: Prof. Dr. Wolfgang D¨unnweber Tag der m¨undlichen Pr¨ufung: 09.03.2010 meiner Familie Abstract Supersymmetry is a hypothetic symmetry between bosons and fermions, which is broken by an unknown mechanism. So far, there is no experimental evidence for the existence of supersymmetric particles. Some Supersymmetry scenarios are predicted to be within reach of the ATLAS detector at the Large Hadron Col- lider. Final states with two isolated leptons (muons and electrons), that have same signs of charge, are suitable for the discovery of supersymmetric cascade decays. There are numerous supersymmetric processes that can yield final states with two same-sign or more leptons. Typically, these processes tend to have long cas- cade decay chains, producing high-energetic jets. Charged leptons are produced from decaying charginos and neutralinos in the cascades. If the R-parity is con- served and the lightest supersymmetric particle is a neutralino, supersymmetric processes lead to a large amount of missing energy in the detector. The most important Standard Model background for the same-sign dilepton channel is the semileptonic decay of top-antitop-pairs. One lepton originates from the leptonic decay of the W boson, the other lepton originates from one of the b quarks. Here, the neutrinos are responsible for the missing energy. The Standard Model background can be strongly reduced by applying cuts on the transverse momenta of jets, on the missing energy and on the lepton isolation.
    [Show full text]
  • Chapter 8. the Atomic Nucleus
    Chapter 8. The Atomic Nucleus Notes: • Most of the material in this chapter is taken from Thornton and Rex, Chapters 12 and 13. 8.1 Nuclear Properties Atomic nuclei are composed of protons and neutrons, which are referred to as nucleons. Although both types of particles are not fundamental or elementary, they can still be considered as basic constituents for the purpose of understanding the atomic nucleus. Protons and neutrons have many characteristics in common. For example, their masses are very similar with 1.0072765 u (938.272 MeV) for the proton and 1.0086649 u (939.566 MeV) for the neutron. The symbol ‘u’ stands for the atomic mass unit defined has one twelfth of the mass of the main isotope of carbon (i.e., 12 C ), which is known to contain six protons and six neutrons in its nucleus. We thus have that 1 u = 1.66054 ×10−27 kg (8.1) = 931.49 MeV/c2 . Protons and neutrons also both have the same intrinsic spin, but different magnetic moments (see below). Their main difference, however, pertains to their electrical charges: the proton, as we know, has a charge of +e , while the neutron has none, as its name implies. Atomic nuclei are designated using the symbol A Z XN , (8.2) with Z, N and A the number of protons (atomic element number), the number of neutrons, and the atomic mass number ( A = Z + N ), respectively, while X is the chemical element symbol. It is often the case that Z and N are omitted, when there is no chance of confusion.
    [Show full text]
  • Mitochondrial Respiratory States and Rates
    MitoFit Preprint Arch (2019) doi:10.26124/mitofit:190001 Posted online 2019-02-12 Open Access Freely available online Mitochondrial respiratory states and rates Gnaiger E, Aasander Frostner E, Abdul Karim N, Abumrad NA, Acuna-Castroviejo D, Adiele RC, Ahn B, Ali SS, Alton L, Alves MG, Amati F, Amoedo ND, Andreadou I, Aragó M, Aragones J, Aral C, Arandarčikaitė O, Armand AS, Arnould T, Avram VF, Bailey DM, Bajpeyi S, Bajzikova M, Bakker BM, Barlow J, Bastos Sant'Anna Silva AC, Batterson P, Battino M, Bazil J, Beard DA, Bednarczyk P, Bello F, Ben-Shachar D, Bergdahl A, Berge RK, Bergmeister L, Bernardi P, Berridge MV, Bettinazzi S, Bishop D, Blier PU, Blindheim DF, Boardman NT, Boetker HE, Borchard S, Boros M, Børsheim E, Borutaite V, Botella J, Bouillaud F, Bouitbir J, Boushel RC, Bovard J, Breton S, Brown DA, Brown GC, Brown RA, Brozinick JT, Buettner GR, Burtscher J, Calabria E, Calbet JA, Calzia E, Cannon DT, Cano Sanchez M, Canto AC, Cardoso LHD, Carvalho E, Casado Pinna M, Cassar S, Cassina AM, Castelo MP, Castro L, Cavalcanti-de-Albuquerque JP, Cervinkova Z, Chabi B, Chakrabarti L, Chakrabarti S, Chaurasia B, Chen Q, Chicco AJ, Chinopoulos C, Chowdhury SK, Cizmarova B, Clementi E, Coen PM, Cohen BH, Coker RH, Collin A, Crisóstomo L, Dahdah N, Dalgaard LT, Dambrova M, Danhelovska T, Darveau CA, Das AM, Dash RK, Davidova E, Davis MS, De Goede P, De Palma C, Dembinska-Kiec A, Detraux D, Devaux Y, Di Marcello M, Dias TR, Distefano G, Doermann N, Doerrier C, Dong L, Donnelly C, Drahota Z, Duarte FV, Dubouchaud H, Duchen MR, Dumas JF,
    [Show full text]
  • Search for Magnetic Monopoles with the Moedal Forward Trapping Detector in 13 Tev Proton-Proton Collisions at the LHC
    week ending PRL 118, 061801 (2017) PHYSICAL REVIEW LETTERS 10 FEBRUARY 2017 Search for Magnetic Monopoles with the MoEDAL Forward Trapping Detector in 13 TeV Proton-Proton Collisions at the LHC B. Acharya,1,2 J. Alexandre,1 S. Baines,3 P. Benes,4 B. Bergmann,4 J. Bernabéu,5 H. Branzas,6 M. Campbell,7 L. Caramete,6 S. Cecchini,8 M. de Montigny,9 A. De Roeck,7 J. R. Ellis,1,10 M. Fairbairn,1 D. Felea,6 J. Flores,11 M. Frank,12 D. Frekers,13 C. Garcia,5 A. M. Hirt,14 J. Janecek,4 M. Kalliokoski,15 A. Katre,16 D.-W. Kim,17 K. Kinoshita,18 A. Korzenev,16 D. H. Lacarrère,7 S. C. Lee,17 C. Leroy,19 A. Lionti,16 J. Mamuzic,5 A. Margiotta,20 N. Mauri,8 N. E. Mavromatos,1 P. Mermod,16,* V. A. Mitsou,5 R. Orava,21 B. Parker,22 L. Pasqualini,20 L. Patrizii,8 G. E. Păvălaş,6 J. L. Pinfold,9 V. Popa,6 M. Pozzato,8 S. Pospisil,4 A. Rajantie,23 R. Ruiz de Austri,5 Z. Sahnoun,8,24 M. Sakellariadou,1 S. Sarkar,1 G. Semenoff,25 A. Shaa,26 G. Sirri,8 K. Sliwa,27 R. Soluk,9 M. Spurio,20 Y. N. Srivastava,28 M. Suk,4 J. Swain,28 M. Tenti,29 V. Togo,8 J. A. Tuszyński,9 V. Vento,5 O. Vives,5 Z. Vykydal,4 T. Whyntie,22,30 A. Widom,28 G. Willems,13 J. H. Yoon,31 and I.
    [Show full text]
  • Review Article STANDARD MODEL of PARTICLE PHYSICS—A
    Review Article STANDARD MODEL OF PARTICLE PHYSICS—A HEALTH PHYSICS PERSPECTIVE J. J. Bevelacqua* publications describing the operation of the Large Hadron Abstract—The Standard Model of Particle Physics is reviewed Collider and popular books and articles describing Higgs with an emphasis on its relationship to the physics supporting the health physics profession. Concepts important to health bosons, magnetic monopoles, supersymmetry particles, physics are emphasized and specific applications are pre- dark matter, dark energy, and new particle discoveries sented. The capability of the Standard Model to provide health (PDG 2008). Many of the students’ questions arise from physics relevant information is illustrated with application of conservation laws to neutron and muon decay and in the misconceptions regarding the Standard Model and its rela- calculation of the neutron mean lifetime. tionship to the field of health physics (Bevelacqua 2008a). Health Phys. 99(5):613–623; 2010 The increasing number and complexity of these questions Key words: accelerators; beta particles; computer calcula- and misconceptions of the Standard Model motivated the tions; neutrons author to write this review article. The intent of this paper is to present the Standard Model to health physicists in a manner that minimizes the INTRODUCTION mathematical complexity. This is a challenge because the THE THEORETICAL formulation describing the properties Standard Model of Particle Physics is a theory of interacting and interactions of fundamental particles is embodied in fields. It contains the electroweak interaction (Glashow the Standard Model of Particle Physics (Bettini 2008; 1961; Weinberg 1967; Salam 1969) and quantum chromo- Cottingham and Greenwood 2007; Guidry 1999; Grif- dynamics (QCD) (Gross and Wilczek 1973; Politzer 1973).
    [Show full text]
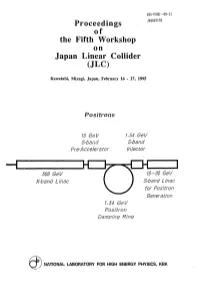
  • Proceedings of the Fifth Workshop on Japan Linear Collider (JLC)
    KEK-PR0C--95-11 Proceedings JP9607178 of the Fifth Workshop on Japan Linear Collider (JLC) Kavvatabi, Miyagi, Japan, February 16 - 17, 1995 Positrons 10 GeV 1.54 GeV S-band S-band Pre-Accelerator Injector 500 GeV 10-30 GeV X-band Linac S-band Linac for Positron Generation 1.54 GeV Positron Damping Ring NATIONAL LABORATORY FOR HIGH ENERGY PHYSICS, KEK KEK Proceedings 95-11 December 1995 A/H Proceedings of the Fifth Workshop on Japan Linear Collider (JLC) Kawatabi, Miyagi, Japan, February 16 - 17, 1995 Editor: Y. Kurihara National Laboratory for High Energy Physics, 1995 KEK Reports are available from: Technical Information & Library National Laboratory for High Energy Physics 1-1 Oho, Tsukuba-shi Ibaraki-ken, 305 JAPAN Phone: 0298-64-1171 Telex: 3652-534 (Domestic) (0)3652-534 (International) Fax: 0298-64-4604 Cable: KEK OHO E-mail: LIBRARY@JPNKEKVX (Bitnet Address) [email protected] (Internet Address) Contents Physics at LEPII T. Tsukamoto 1 Present Status of 1.54 GeV ATF Linac S.Takeda 12 Button-type beam-position monitor for the ATF damping ring F. Hinode 28 Recent progress on cathode development and gun development at Nagoya and KEK M.Tawada 31 Development of polarized e+ beams for future linear colliders M. Chiba 38 The LASER beams with very long focal depth for photon-photon collider K. Matsukado 78 An interactive version of GRACE and catalogue of e+e- interactions as its application S.Kawabata 92 The GRACE system for SUSY processes M. Jimbo 98 Search for dynamical symmetry breaking physics by using top quark T.
    [Show full text]
  • Effects of Volume Corrections and Resonance Decays on Cumulants of Net-Charge Distributions in a Monte Carlo Hadron Resonance Gas Model
    Physics Letters B 765 (2017) 188–192 Contents lists available at ScienceDirect Physics Letters B www.elsevier.com/locate/physletb Effects of volume corrections and resonance decays on cumulants of net-charge distributions in a Monte Carlo hadron resonance gas model Hao-jie Xu Department of Physics and State Key Laboratory of Nuclear Physics and Technology, Peking University, Beijing 100871, China a r t i c l e i n f o a b s t r a c t Article history: The effects of volume corrections and resonance decays (the resulting correlations between positive Received 27 September 2016 charges and negative charges) on cumulants of net-proton distributions and net-charge distributions Received in revised form 20 November 2016 are investigated by using a Monte Carlo hadron resonance gas (MCHRG) model. The required volume Accepted 7 December 2016 distributions are generated by a Monte Carlo Glauber (MC-Glb) model. Except the variances of net- Available online 12 December 2016 charge distributions, the MCHRG model with more realistic simulations of volume corrections, resonance Editor: J.-P. Blaizot decays and acceptance cuts can reasonably explain the data of cumulants of net-proton distributions and net-charge distributions reported by the STAR collaboration. The MCHRG calculations indicate that both the volume corrections and resonance decays make the cumulant products of net-charge distributions deviate from the Skellam expectations: the deviations of Sσ and κσ2 are dominated by the former effect while the deviations of ω are dominated by the latter one. © 2016 The Author(s). Published by Elsevier B.V. This is an open access article under the CC BY license (http://creativecommons.org/licenses/by/4.0/).
    [Show full text]
  • Chapter 2 Atoms, Molecules, and Ions 67
    Chapter 2 Atoms, Molecules, and Ions 67 Chapter 2 Atoms, Molecules, and Ions Figure 2.1 Analysis of molecules in an exhaled breath can provide valuable information, leading to early diagnosis of diseases or detection of environmental exposure to harmful substances. (credit: modification of work by Paul Flowers) Chapter Outline 2.1 Early Ideas in Atomic Theory 2.2 Evolution of Atomic Theory 2.3 Atomic Structure and Symbolism 2.4 Chemical Formulas 2.5 The Periodic Table 2.6 Molecular and Ionic Compounds 2.7 Chemical Nomenclature Introduction Your overall health and susceptibility to disease depends upon the complex interaction between your genetic makeup and environmental exposure, with the outcome difficult to predict. Early detection of biomarkers, substances that indicate an organism’s disease or physiological state, could allow diagnosis and treatment before a condition becomes serious or irreversible. Recent studies have shown that your exhaled breath can contain molecules that may be biomarkers for recent exposure to environmental contaminants or for pathological conditions ranging from asthma to lung cancer. Scientists are working to develop biomarker “fingerprints” that could be used to diagnose a specific disease based on the amounts and identities of certain molecules in a patient’s exhaled breath. An essential concept underlying this goal is that of a molecule’s identity, which is determined by the numbers and types of atoms it contains, and how they are bonded together. This chapter will describe some of the fundamental chemical principles related to the composition of matter, including those central to the concept of molecular identity. 68 Chapter 2 Atoms, Molecules, and Ions 2.1 Early Ideas in Atomic Theory By the end of this section, you will be able to: • State the postulates of Dalton’s atomic theory • Use postulates of Dalton’s atomic theory to explain the laws of definite and multiple proportions The language used in chemistry is seen and heard in many disciplines, ranging from medicine to engineering to forensics to art.
    [Show full text]