DOCSLIB.ORG

Link to Full Text

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Link to Full Text ~ .......... ~ ~ - - -- .. ~~ -- .... ..... .., - .. - ... ...., .... IX. ADYNAMIC HESEHV01H SIMULATION MODEL-DYHESM:5 i\ 311 c. transverse and longitUdinal direction playa secondary role and only the variations) ." I in the vertical enter lhe first order balances of mass, momentum and energy. 1/ I Departures from this Stilte of horizontalisopyc'nalsare possible, but these \ tI l A DYNAMIC RESERVOIR SIl\olULATION MODEL ­ enter only as isolated events or as \I/eak pe.!lurbatiQ.D.S. In both cases the.•net eJJ;cJ,J CI DYRESM: 5 is e~plured wi(h a parame!efizalion of their inp,ut (0 the vertical s(rUelure"iiild , ) I comparison of the model prediction and field data must thus be confined to ~ ~ .....of.............,.calm when the structure is truly one-dimensional. lorg 1mberger and John C.. Pattetsun .. ~ ,. The constraints imposed by ~uch a one-dimer.:Jional model may best be University of Western Australia quantified by defining a series of non-dimensional llUmbers. The value of the Nedlands, Western Australia Wedderburn number :) LV =.i.!!.. h (.J" I I '( 14.2 • L- '7 y(l .. n, (I) , \ ..,' I / 1. INTRODUCTION where g' is an effective reoufed gravity across the thermocline, h the depth of the mixed layer, L the basin scale, and u· the surface shear velocity, is a measure of """·".',j<}·,t-·;~·'",,,"~~,'ti The dynamic reservoir simulation model, DYRESM, is a one-dimensional the activity within the mixed layer. Spigel and Imberger (I980) have shown thah, numerical model for the prediction of temperature and salinity in small to medium for W > 00) the departure fmm one-dimensionality is minimal and for I ':I­ sized reservoirs and Jakes. The model was constructed toiorm a suitable basis for 0(11/ L) < W< 0(1) the departure is severe but may be successfully parameter- r 17 I ized. For W < O(h/L) the lake ove!1urns,- " • I, I a more general water quality model. The requirements imposed by this aim are J':~I made by Imberger (1978), who shows that for both substances with a fast tumo,ter Inflows do not lead to severe vertical motions in the bulk of the reservoir I lime such as phytoplankton and for conservative substances such as salt, the mix­ provided the internal Froude number ing mechanisms within the reservoir must be modeled accurately. Not only must a -- .mOdelbe.capable of predicting, the~v~ Y~rlieal tri!illifer--!!.t:.J!1.!!~.'0!~"~~ ~roi~ U <1 and the subsequent flow processes, but it must also be capable of F; = .Jg'H (2) Iresolving individual mixing regioos. - - -.----. This is a great departure from what has been assumed to date. Previously it I has been generally accepted that once a partkular reservoir model was capable of where U is the inflow velocity, g' the reduced gravity between the surface reser­ being tuned to correctly predict the vertical temperature profiles over a particular voir Water and the inflow and H the reservoir depth. study period, that this then constituted a reliable model for the purposes of water The outflow dynamics..is governed by a similar Froude number criterion I quality modeling. However, as discussed in Fischer et al., (1979) this is not the case since gif'f~r~I]t paraml;t~r~are dependent on different mixing Qro.9~sses fQ[ f~ = Q their. dis~ributio!l. g,I/2Hs/2 < 1 (3) The problem confronting the modeler is thus difficult. On the one hand the model should be widely applicable and cheap to run, and on the other it must cap' where Q is the outflow discharge and g' the reduced gravity between the surface ture the mixing induced by the small ·scales of motion. The marriage of these and bottom water. seemingly conflicting aims requires careful consideration of not only the concept I Laslly, the earth '5 rotation will not lead to vertical motions if J but also the architecture ora proposed--model. Although increasing availability oi' I . computing power has led to an increased potential for application of two or three- dimensional reservoir models, the required !]§.Ql!Jlio_1h. down to centimeters and g'8 minutes, is not currently possible within the context of long term simulations, and f 2B 2 < (4) I aor.e-dimensional model appears to be the only realistic option. 7 l F • I' -~ >Thelli.Qng stratification normally found in 2.m.all to lUe.t!ium sized reservoirs where g'is the effective reduced gravity over the depth 8, the scale bf the ~lucity A r may be used to advantage. strong stratiJicallon of the water inhibits vertical .toncell1ral.ious~ I ,IS the Coriolis parameter and B is the maximum width of the lake. - I~ c motions and reduces the turbulence to intermittent bursts. For such lakes the I~"··"'·:'I • ~ ~ (-t1I'IIll(hl InKI "l AIl"lt'U!IL'I'I~ ~ III'" • nllllWI '>lOll ::.~J ' 'lill \u ,I. I 1".I,f,I"'- 1Jt,lh\ JO.HI ri • •_,:, ...... ___ I' 4' ••:->4 J ""., '- ' L t t' . " -\~;:fi'l!f~.$$'- rt~~ i~lX~) 1l'~ '~~";. ~~"" ~~.L_~·~." ~"~'~.:. .. .. 1' "'_ ....... .. '.. r ~~- >t-....-,...:.-.;,._-:.~,. _~~,:~~~-_.;_:~'>:~....--.-. _.;,.._~. ~~,._.~,,--, ~-::""· _-~---c-"i -~ ~"_., ~~. "-~. ~ ~;;.~r't."": .:.:~-r:_',:~" ·?>-,-<~~~':;4.14>4$i.,:j;;'~~,4:t.~;. tf"''''''. __ ... __ ....... ..l .. , ....... -Q,'- "" - r, . ,':'-",'-':' ,;;:/-',) . ~ ~ ~ 312 JOHG IMBEHGEH AND JOHN C. PAT'l'E.\SON IX. A DYNAMIC HESEHVOm SIMULATION MODEL-DYRESM:5 313 Within these constraints DYRESM yields an llccurate descriplion of the 2. DY.R.E~M MAIN PROGRAM dynamics governing the verlical structure in a lake. It must, however, always be emphasized that superimposed on the structure predicted by DYRESM there are I 12[£'h&~ The model DYRESM is cocstructed as a main program with :mbroutines \ mixini which have only a second order influence on the vertical slruc­ which separately model each of the -e.hY~'!!..PJ~~se~ .of inflow, withdrawal, mixed !tures, but which are the first order mechanisms for transporting subslances hor- layer dynamics, and vertical transport in the hypolimnion. In addition, thm'e are a .~. I izontally. These find their origins in _~.!Wan~~~ .b~~timt al!..<!.£Q.oHng at the edge of. number of service subroutines which provide maintenance of the layer sllslem !he.1,!~-e, c!ir~t ~ nd .Shd.~iillL.bY~ ri.Q~ ')' r surt1!ce runoff. sheiterinu mountain. .. (volumes, positions, etc.). and provide calculations of physical propertk,s which are and boundary mixing in the hypolimnion, Only the influence of these processes frequently required such as density. The functions of the main program are the;,'e­ on the one-dimensional structure is modeled by DYRESM, A separate perturba­ fore those of input/output, the calculation of fixed parameters. and control over tion scheme is required to reveal their influence on horizontal varialions in n reser­ timing of the calls to the various process subroutines. voir. The firslorder vertical structure computed with DYRESM may in future investigations be used to compute such hgrizontul traosQoftprocesses. These may The question of how frequently the process. subroutines should be called \ D t natu.rally arises, For-.!!lost purposes., a ,gailY pl1(diction of th~JhermaLstruc;tur.e..is.I." be modeled with a simplified three-dimensional model using the one-dimensional ~uffl~i~.nl~ 'yasi~ ~of vertical structure as the mean density field. and the time the model is set to this value. Since the 1 inflow and outflow volumes change only slowly~ generally over a few days at least, I' <k Even the one-dimensional problem is oot simple. A uniform gr:rt model this basic lime step is also suitable for lhese processes, and Ihe appropriate subroll- . which resolves lhese fine scales over the whole depth would require a large tines are cal1ed~..93jJy. On the other hand, the mixed layer dynamics covers number of mesh points and computation would be slow, to say nothing about scales very much shorler than one day, and e.ven thOu.g.h. dailY. ave.r.aged meteoro-j problems of stability and numerical diffusion. Even if local compaction of a wider logical inputs ... e mo!)~!v used, the mixed layer model subroutines need to be grid were employed. which introduces its own problems. the model at any instant ~alled more frequently tQ m~tch the response-of the'diurna"ideepening. would have only an estimate of where the compaction was required for each pro­ cess,and since several processes may occur at different positions simultaneously, Thus the model incorporates ,two time steps; a fixed basic giep 0: ~>ne day and ) v' little advantage would be gained. a ~ariable. syeb-d:illK. time st~PJorJ1!e_ mixing algorllhm. The length of this sub- .I 2lliL9y'ar~~r...baur I: I I I dally step IS determmed by the dynamiCs and ranges between i!nJ I' t -;lith these considerations in mind. the model DYRESM was dey'eloped by ~elye. ho.!:'~!Jf averaged data is used, This procedure allows small time steps Jl.-/, Imberf: "r et al. (1978) with a different approach to the task. Concentrating on 4' when the dynamics so require; in less critical periods, the time step expands "paraJTI.I:!~erizatioJLQL th~'physical proSS&~k~Lrather than numerical solution of the without loss in accuracy. appropriate differential eq'uations, DYRESM makes use of a layer concept, in which the reservoir is modeled as a ,.System..of !!.orizoo.taLJ<lYers_of uniform pro", DYRESM is then organized in the fOllowing way (see Flowchart 2.0. The per!y..~ These layers move up and down, adjusting their thickness in accordance main program inputs the fixed data; physical dimensions, volume and area as a with the volume-:depth relationship, as inflow and withdrawal increase and decrease function of depth, physical properties of the inflowing streams, locations of the the reservoir volume.
Load more

Recommended publications
  • KR/KL Burbot Conservation Strategy
    January 2005 Citation: KVRI Burbot Committee. 2005. Kootenai River/Kootenay Lake Conservation Strategy. Prepared by the Kootenai Tribe of Idaho with assistance from S. P. Cramer and Associates. 77 pp. plus appendices. Conservation strategies delineate reasonable actions that are believed necessary to protect, rehabilitate, and maintain species and populations that have been recognized as imperiled, but not federally listed as threatened or endangered under the US Endangered Species Act. This Strategy resulted from cooperative efforts of U.S. and Canadian Federal, Provincial, and State agencies, Native American Tribes, First Nations, local Elected Officials, Congressional and Governor’s staff, and other important resource stakeholders, including members of the Kootenai Valley Resource Initiative. This Conservation Strategy does not necessarily represent the views or the official positions or approval of all individuals or agencies involved with its formulation. This Conservation Strategy is subject to modification as dictated by new findings, changes in species status, and the completion of conservation tasks. 2 ACKNOWLEDGEMENTS The Kootenai Tribe of Idaho would like to thank the Kootenai Valley Resource Initiative (KVRI) and the KVRI Burbot Committee for their contributions to this Burbot Conservation Strategy. The Tribe also thanks the Boundary County Historical Society and the residents of Boundary County for providing local historical information provided in Appendix 2. The Tribe also thanks Ray Beamesderfer and Paul Anders of S.P. Cramer and Associates for their assistance in preparing this document. Funding was provided by the Bonneville Power Administration through the Northwest Power and Conservation Council’s Fish and Wildlife Program, and by the Idaho Congressional Delegation through a congressional appropriation administered to the Kootenai Tribe by the Department of Interior.
    [Show full text]
  • Ethnohistory of the Kootenai Indians
    University of Montana ScholarWorks at University of Montana Graduate Student Theses, Dissertations, & Professional Papers Graduate School 1983 Ethnohistory of the Kootenai Indians Cynthia J. Manning The University of Montana Follow this and additional works at: https://scholarworks.umt.edu/etd Let us know how access to this document benefits ou.y Recommended Citation Manning, Cynthia J., "Ethnohistory of the Kootenai Indians" (1983). Graduate Student Theses, Dissertations, & Professional Papers. 5855. https://scholarworks.umt.edu/etd/5855 This Thesis is brought to you for free and open access by the Graduate School at ScholarWorks at University of Montana. It has been accepted for inclusion in Graduate Student Theses, Dissertations, & Professional Papers by an authorized administrator of ScholarWorks at University of Montana. For more information, please contact [email protected]. COPYRIGHT ACT OF 1976 Th is is an unpublished m a n u s c r ip t in w h ic h c o p y r ig h t su b ­ s i s t s . Any further r e p r in t in g of it s c o n ten ts must be a ppro ved BY THE AUTHOR. MANSFIELD L ib r a r y Un iv e r s it y of Montana D a te : 1 9 8 3 AN ETHNOHISTORY OF THE KOOTENAI INDIANS By Cynthia J. Manning B.A., University of Pittsburgh, 1978 Presented in partial fu lfillm en t of the requirements for the degree of Master of Arts UNIVERSITY OF MONTANA 1983 Approved by: Chair, Board of Examiners Fan, Graduate Sch __________^ ^ c Z 3 ^ ^ 3 Date UMI Number: EP36656 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted.
    [Show full text]
  • Main Arm Kootenay Lake FIM 2011
    Foreshore Inventory and 3Mapping KKOOOOTTEENNAAYY LLAAKKEE MMAAIINN AARRMM Prepared For: Regional District of Central Kootenay Prepared By: Ecoscape Environmental Consultants Ltd. September, 2010 File No.: 09-513 #102 – 450 Neave Court Kelowna, BC V1V 2M2 Phone: 250.491.7337 Fax: 250.491.7772 Email: [email protected] FORESHORE INVENTORY AND MAPPING Regional District of Central Kootenay Kootenay Lake Main Arm Prepared For: Regional District of Central Kootenay Box 590, 202 Lakeside Dr. Nelson, BC V1L 5R4 Prepared By: ECOSCAPE ENVIRONMENTAL CONSULTANTS LTD. #102 – 450 Neave Court Kelowna, B.C. V1W 3A1 January 2011 File No. 09-513 #102 – 450 Neave Ct. Kelowna BC. V1V 2M2 ph: 250.491.7337 fax: 250.491.7772 [email protected] 09-513 i January 2011 ACKNOWLEDGEMENTS This project was made possible through collaboration between the Regional District of Central Kootenay and Fisheries and Oceans Canada. The following parties carried out or organized fieldwork for this assessment: Fisheries and Oceans Canada: Bruce MacDonald, Sheldon Romaine, Brian Ferguson, Kristin Murphy, and Darryl Hussey The author of this report was: Jason Schleppe, M.Sc., R.P.Bio. (Ecoscape) The report was reviewed by: Kyle Hawes, B.Sc., R.P.Bio. (Ecoscape) Geographical Information Systems (GIS) mapping and analysis was prepared by: Robert Wagner, B.Sc. (Ecoscape) Recommended Citation: Schleppe, J., 2009. Kootenay Lake Foreshore Inventory and Mapping. Ecoscape Environmental Consultants Ltd.. Project File: 09-513. September, 2010. Prepared for: Regional District Central Kootenay. #102 – 450 Neave Ct. Kelowna BC. V1V 2M2 ph: 250.491.7337 fax: 250.491.7772 [email protected] 09-513 ii January 2011 EXECUTIVE SUMMARY This report has been prepared based upon the belief that it is possible to manage our watersheds and their natural surroundings in a sustainable manner.
    [Show full text]
  • BC Hydro Climate Change Assessment Report 2012
    POTENTIAL IMPACTS OF CLIMATE CHANGE ON BC HYDRO’S WATER RESOURCES Georg Jost: Ph.D., Senior Hydrologic Modeller, BC Hydro Frank Weber; M.Sc., P. Geo., Lead, Runoff Forecasting, BC Hydro 1 EXecutiVE Summary Global climate change is upon us. Both natural cycles and anthropogenic greenhouse gas emissions influence climate in British Columbia and the river flows that supply the vast majority of power that BC Hydro generates. BC Hydro’s climate action strategy addresses both the mitigation of climate change through reducing our greenhouse gas emissions, and adaptation to climate change by understanding the risks and magnitude of potential climatic changes to our business today and in the future. As part of its climate change adaptation strategy, BC Hydro has undertaken internal studies and worked with some of the world’s leading scientists in climatology, glaciology, and hydrology to determine how climate change affects water supply and the seasonal timing of reservoir inflows, and what we can expect in the future. While many questions remain unanswered, some trends are evident, which we will explore in this document. 2 IMPACTS OF CLIMATE CHANGE ON BC HYDRO-MANAGED WATER RESOURCES W HAT we haVE seen so far » Over the last century, all regions of British Columbia »F all and winter inflows have shown an increase in became warmer by an average of about 1.2°C. almost all regions, and there is weaker evidence »A nnual precipitation in British Columbia increased by for a modest decline in late-summer flows for those about 20 per cent over the last century (across Canada basins driven primarily by melt of glacial ice and/or the increases ranged from 5 to 35 per cent).
    [Show full text]
  • RG 42 - Marine Branch
    FINDING AID: 42-21 RECORD GROUP: RG 42 - Marine Branch SERIES: C-3 - Register of Wrecks and Casualties, Inland Waters DESCRIPTION: The finding aid is an incomplete list of Statement of Shipping Casualties Resulting in Total Loss. DATE: April 1998 LIST OF SHIPPING CASUALTIES RESULTING IN TOTAL LOSS IN BRITISH COLUMBIA COASTAL WATERS SINCE 1897 Port of Net Date Name of vessel Registry Register Nature of casualty O.N. Tonnage Place of casualty 18 9 7 Dec. - NAKUSP New Westminster, 831,83 Fire, B.C. Arrow Lake, B.C. 18 9 8 June ISKOOT Victoria, B.C. 356 Stranded, near Alaska July 1 MARQUIS OF DUFFERIN Vancouver, B.C. 629 Went to pieces while being towed, 4 miles off Carmanah Point, Vancouver Island, B.C. Sept.16 BARBARA BOSCOWITZ Victoria, B.C. 239 Stranded, Browning Island, Kitkatlah Inlet, B.C. Sept.27 PIONEER Victoria, B.C. 66 Missing, North Pacific Nov. 29 CITY OF AINSWORTH New Westminster, 193 Sprung a leak, B.C. Kootenay Lake, B.C. Nov. 29 STIRINE CHIEF Vancouver, B.C. Vessel parted her chains while being towed, Alaskan waters, North Pacific 18 9 9 Feb. 1 GREENWOOD Victoria, B.C. 89,77 Fire, laid up July 12 LOUISE Seaback, Wash. 167 Fire, Victoria Harbour, B.C. July 12 KATHLEEN Victoria, B.C. 590 Fire, Victoria Harbour, B.C. Sept.10 BON ACCORD New Westminster, 52 Fire, lying at wharf, B.C. New Westminster, B.C. Sept.10 GLADYS New Westminster, 211 Fire, lying at wharf, B.C. New Westminster, B.C. Sept.10 EDGAR New Westminster, 114 Fire, lying at wharf, B.C.
    [Show full text]
  • Wetland Action Plan for British Columbia
    Wetland Action Plan for British Columbia IAN BARNETT Ducks Unlimited Kamloops, 954 A Laval Crescent, Kamloops, BC, V2C 5P5, Canada, email [email protected] Abstract: In the fall of 2002, the Wetland Stewardship Partnership was formed to address the need for improved conservation of wetland ecosystems (including estuaries) in British Columbia. One of the first exercises undertaken by the Wetland Stewardship Partnership was the creation of a Wetland Action Plan. The Wetland Action Plan illustrates the extent of the province's wetlands, describes their value to British Columbians, assesses threats to wetlands, evaluates current conservation initiatives, and puts forth a set of specific actions and objectives to help mitigate wetland loss or degradation. It was determined that the most significant threats to wetlands usually come from urban expansion, industrial development, and agriculture. The Wetland Stewardship Partnership then examined which actions would most likely have the greatest positive influence on wetland conservation and restoration, and listed nine primary objectives, in order of priority, in a draft ‘Framework for Action’. Next, the partnership determined that meeting the first four of these objectives could be sufficient to provide meaningful and comprehensive wetland protection, and so, committed to working together towards enacting specific recommendations in relation to these objectives. These four priority objectives are as follows: (1) Work effectively with all levels of government to promote improved guidelines and stronger legislative frameworks to support wetlands conservation; (2) Provide practical information and recommendations on methods to reduce impacts to wetlands to urban, rural, and agricultural proponents who wish to undertake a development in a wetland area; (3) Improve the development and delivery of public education and stewardship programs that encourage conservation of wetlands, especially through partnerships; and (4) Conduct a conservation risk assessment to make the most current inventory information on the status of B.C.
    [Show full text]
  • The 5Th Annual West Kootenay Glacier Challenge Scotiabank MS Bike Tour!
    The 5th Annual West Kootenay Glacier Challenge Scotiabank MS Bike Tour Courtesy of: Nelson & District Chamber of Commerce 91 Baker Street Nelson B.C. Ph. 250 352 3433 [email protected] discovernelson.com Scotiabank MS Bike Tour August 20-21, 2016 The tour starts in New Denver… Slocan Valley… New Denver- Founded upon the discovery of silver in the mountains adjacent to Slocan Lake in 1891, prospectors from the United States came flooding up to the New Denver region in 1892 to stake their claims, and gather their riches. New Denver quickly grew to a population of 500 people with 50 buildings. In 1895 this growing community built government offices and supply houses for the Silvery Slocan Mines. “A Simple Curve” was filmed in and around the Slocan Valley and was debuted in 2005. The story is of a young man born to war resister parents. War Resisters- In 1976 as many as 14,000 Americans came to the Slocan Valley in an attempt to avoid the Vietnam War. About half of those who made the move were self-proclaimed war resisters, many of whom settled in the Kootenay Region. Nikkei Internment Memorial Centre This exclusive interpretive centre features the Japanese-Canadian internment history of New Denver during the Second World War. The camp is said to have held close to 1500 internees during the war. The memorial centre opened in 1994, which showcases several buildings including the community hall and three restored tar paper shacks with Japanese gardens. A well known Canadian to come out of one of these local institutions is Dr.
    [Show full text]
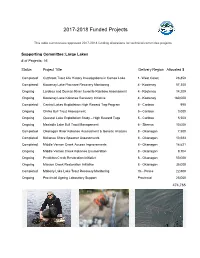
  • Funded Projects 2017-2018
    2017-2018 Funded Projects This table summarizes approved 2017-2018 funding allocations for technical committee projects. Supporting Committee: Large Lakes # of Projects: 16 Status Project Title Delivery Region Allocated $ Completed Cutthroat Trout Life History Investigations in Comox Lake 1- West Coast 26,858 Completed Kootenay Lake Piscivore Recovery Monitoring 4 - Kootenay 57,300 Ongoing Lardeau and Duncan River Juvenile Rainbow Assessment 4 - Kootenay 14,209 Ongoing Kootenay Lake Kokanee Recovery Initiative 4 - Kootenay 180,000 Completed Central Lakes Exploitation High Reward Tag Program 5 - Cariboo 990 Ongoing Chilko Bull Trout Assessment 5 - Cariboo 3,000 Ongoing Quesnel Lake Exploitation Study – High Reward Tags 5 - Cariboo 5,500 Ongoing Meziadin Lake Bull Trout Management 6 - Skeena 10,000 Completed Okanagan River Kokanee Assessment & Genetic Analysis 8 - Okanagan 7,500 Completed Kokanee Shore Spawner Assessments 8 - Okanagan 10,583 Completed Middle Vernon Creek Access Improvements 8 - Okanagan 16,621 Ongoing Middle Vernon Creek Kokanee Enumeration 8 - Okanagan 9,704 Ongoing Penticton Creek Restoration Initiative 8 - Okanagan 50,000 Ongoing Mission Creek Restoration Initiative 8 - Okanagan 35,000 Completed Moberly Lake Lake Trout Recovery Monitoring 7b - Peace 22,500 Ongoing Provincial Ageing Laboratory Support Provincial 25,000 474,765 sr_images_rivers Delivery Region Locations image credit: frontcounterbc.com 2017-2018 Large Lakes Projects Page 2 Cutthroat Trout Life History Investigations in Comox Lake Status: Completed Cutthroat trout from Comox Lake were captured and tagged through the spring, summer, and fall periods of 2016 and 2017 (n=309). A sub-sample of captured individuals were marked using passive integrated transponder (PIT) tags (n=120) and a combination of low-reward and high-reward floy tags (179).
    [Show full text]
  • Pump out Feasibility Study Summary
    www.klsb.org email [email protected] Kootenay Lake Sustainable Boating Society Marine Pump-out Feasibility Study Columbia Basin Trust File #3987 Environmental Initiatives Program Executive Summary A. Background and Project Description This project was proposed and developed as a result of the common understanding by the boating industry of the need for sewage pump-out availability and the lack of such services on Kootenay Lake. The removal of barriers to environmental stewardship are known to help motivate appropriate choices for sustainable Work Plan 1. Two independent contractors were selected of the several referred by the chair of the South Kootenay Lake Community Connections Society. Contractors were Branca Lewendowski who worked on the marina survey and Janice Cooper who initiated conversations with marina operators and submitted press releases. Consent of marina operators allowed KLSB to publish their data on the KLSB website. In-kind support was contributed by Lois Wakelin, KLSB director, and Cheryl Graham, KLSB director, who managed website development. Director Lois Wakelin assisted with research regarding number of potential boaters on the lake. 2. Boating organizations such as the Kootenay Lake Sailing Association and the Nelson Boaters Club were contacted. 3. Masse Environmental Consultants, Inc. was contracted to research physical and legal requirements, equipment manufacturers, estimated costs, and cost recovery analysis. Director Lois Wakelin provided additional research data related to equipment, boating capacity, cost recovery, and review. cost recovery, and review. Ms. Wakelin also reviewed the consultant’s report for fulfillment of project goals. 4. Feasible locations were determined based on surveys of marina operators and boater responses, and physical viewing.
    [Show full text]
  • Kootenay Lake Fertilization Experiment, Years 11 and 12(2002 and 2003)
    KOOTENAY LAKE FERTILIZATION EXPERIMENT, YEARS 11 AND 12(2002 AND 2003) by E. U. Schindler, K. I. Ashley, R. Rae, L. Vidmanic, H. Andrusak, D. Sebastian, G. Scholten, P. Woodruff, F. Pick, L. M. Ley and P. B. Hamilton. Fisheries Project Report No. RD 114 2006 Fish and Wildlife Science and Allocation Ministry of Environment Province of British Columbia Major Funding by Fish and Wildlife Compensation Program - Columbia Basin Fisheries Project Reports frequently contain preliminary data, and conclusions based on these may be subject to change. Reports may be cited in publications but their manuscript status (MS) must be noted. Please note that the presentation summaries in the report are as provided by the authors, and have received minimal editing. Please obtain the individual author's permission before citing their work. KOOTENAY LAKE FERTILIZATION EXPERIMENT, YEARS 11 AND 12 (2002 AND 2003) by E. U. Schindler1, K. I. Ashley2, R. Rae3, L. Vidmanic4, H. Andrusak5, D. Sebastian6, G. Scholten6, P. Woodruff7, F. Pick8, L. M. Ley9 and P. B. Hamilton9. 1 Fish and Wildlife Science and Allocation Section, Ministry of Environment, Province of BC, 401-333 Victoria St., Nelson, BC, V1L 4K3 2 Department of Civil Engineering, University of British Columbia, 2324 Main Mall, Vancouver, B.C. V6T 1W5 3 Sumac Writing & Editing, 9327 Milne RD, Summerland, BC V0H 1Z7 4 Limno-Lab Ltd., 506-2260 W.10th Ave., Vancouver, BC V6K 2H8 5 Redfish Consulting Ltd., 5244 Hwy 3A, Nelson, BC, V1L 6N6 6 Aquatic Ecosystem Science Section, Biodiversity Branch Ministry of Environment, Province of BC PO Box 9338 STN PROV GOVT, Victoria, BC, V8W 9M2 7 Biological Contractor, BC Conservation Foundation, 206-17564 56th Ave., Surrey, BC, V3S 4X5 8 University of Ottawa, Department of Biology, Ottawa, ON, K1N 6N5 9 Canadian Museum of Nature, P.
    [Show full text]
  • Kootenay Lake Sustainable Boating Sewage Pump-Out Project
    Kootenay Lake Sustainable Boating Sewage Pump-Out Project Prepared for: Kootenay Lake Sustainable Boating Society Prepared by: Masse Environmental Consultants Ltd. 812 Vernon St Nelson, BC V1L 4G4 September 2012 Kootenay Lake Sustainable Boating Sewage Pump-Out Project Table of Contents 1 Introduction ............................................................................................................. 3 2 Background .............................................................................................................. 3 2.1 Environmental Impacts .......................................................................................................... 3 2.2 Legislation and Regulations .................................................................................................... 4 3 Permitting Process ................................................................................................... 5 3.1 Sewage Pump-out Stations ..................................................................................................... 5 3.2 Dock and Boathouse Construction in Freshwater Systems ........................................................ 5 4 Proposed Sewage Pump-out site locations ............................................................. 6 5 Types of Pump-out Systems .................................................................................... 7 5.1 Diaphragm Pump ................................................................................................................... 8 5.2 Peristaltic Pump
    [Show full text]
  • The Village of Kaslo Celebrates 125 Years As an Incorporated Municipality
    May 12, 2018 • VOL. II – NO. 1 • The Kaslo Claim The VOL.Kaslo II – NO. I • KASLO, BRITISH COLUMBIA • MAYClaim 12, 2018 The Village of Kaslo Celebrates 125 Years as an Incorporated Municipality by Jan McMurray are finding ways to celebrate Kaslo’s Kaslo Pennywise beginning on June decorated in Kaslo colours and flags The Langham has commissioned The municipality of Kaslo will quasquicentennial, as well. Can you 5. The person who finds the treasure from around the world, and guided Lucas Myers to write a one-man, reach the grand old age of 125 on guess the theme of Kaslo May Days will keep the handcrafted box and the walking tours of Kaslo River Trail. multimedia play, Kaslovia: A August 14, and a number of events this year? Watch for the Village’s float, $100 bill inside. A Treasure Fund is The North Kootenay Lake Arts Beginner’s Guide, which he will are being planned to celebrate this the mini Moyie, and the refurbished right now growing with donations, and Heritage Council will host perform on Friday, September 28 momentous occasion. Maypole float in the parade. There and is expected to exceed $1,500 by a special arts and crafts table on and Saturday, September 29 at the The Kaslo 125 Committee is will be new costumes handmade by the time the box is found. The bulk of August 11 at the Saturday Market. Langham. Myers’ one-man plays are planning a gala event at the Legion Elaine Richinger for the Maypole the fund will go to the finder’s charity People will be invited to do an on- simply too good to miss – mark your on Saturday, August 11 and a Street Dancers and new ribbons from of choice, with five per cent awarded the-spot art project with a Kaslo calendars now! Party on Fourth Street and City Hall England for the Maypole.
    [Show full text]