Differential Geometry Curves – Surfaces – Manifolds Third Edition
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Toponogov.V.A.Differential.Geometry
Victor Andreevich Toponogov with the editorial assistance of Vladimir Y. Rovenski Differential Geometry of Curves and Surfaces A Concise Guide Birkhauser¨ Boston • Basel • Berlin Victor A. Toponogov (deceased) With the editorial assistance of: Department of Analysis and Geometry Vladimir Y. Rovenski Sobolev Institute of Mathematics Department of Mathematics Siberian Branch of the Russian Academy University of Haifa of Sciences Haifa, Israel Novosibirsk-90, 630090 Russia Cover design by Alex Gerasev. AMS Subject Classification: 53-01, 53Axx, 53A04, 53A05, 53A55, 53B20, 53B21, 53C20, 53C21 Library of Congress Control Number: 2005048111 ISBN-10 0-8176-4384-2 eISBN 0-8176-4402-4 ISBN-13 978-0-8176-4384-3 Printed on acid-free paper. c 2006 Birkhauser¨ Boston All rights reserved. This work may not be translated or copied in whole or in part without the writ- ten permission of the publisher (Birkhauser¨ Boston, c/o Springer Science+Business Media Inc., 233 Spring Street, New York, NY 10013, USA) and the author, except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and re- trieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed in the United States of America. (TXQ/EB) 987654321 www.birkhauser.com Contents Preface ....................................................... vii About the Author ............................................. -

Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission. -

History of Mathematics
Georgia Department of Education History of Mathematics K-12 Mathematics Introduction The Georgia Mathematics Curriculum focuses on actively engaging the students in the development of mathematical understanding by using manipulatives and a variety of representations, working independently and cooperatively to solve problems, estimating and computing efficiently, and conducting investigations and recording findings. There is a shift towards applying mathematical concepts and skills in the context of authentic problems and for the student to understand concepts rather than merely follow a sequence of procedures. In mathematics classrooms, students will learn to think critically in a mathematical way with an understanding that there are many different ways to a solution and sometimes more than one right answer in applied mathematics. Mathematics is the economy of information. The central idea of all mathematics is to discover how knowing some things well, via reasoning, permit students to know much else—without having to commit the information to memory as a separate fact. It is the reasoned, logical connections that make mathematics coherent. The implementation of the Georgia Standards of Excellence in Mathematics places a greater emphasis on sense making, problem solving, reasoning, representation, connections, and communication. History of Mathematics History of Mathematics is a one-semester elective course option for students who have completed AP Calculus or are taking AP Calculus concurrently. It traces the development of major branches of mathematics throughout history, specifically algebra, geometry, number theory, and methods of proofs, how that development was influenced by the needs of various cultures, and how the mathematics in turn influenced culture. The course extends the numbers and counting, algebra, geometry, and data analysis and probability strands from previous courses, and includes a new history strand. -

A Comparison of Differential Calculus and Differential Geometry in Two
1 A Two-Dimensional Comparison of Differential Calculus and Differential Geometry Andrew Grossfield, Ph.D Vaughn College of Aeronautics and Technology Abstract and Introduction: Plane geometry is mainly the study of the properties of polygons and circles. Differential geometry is the study of curves that can be locally approximated by straight line segments. Differential calculus is the study of functions. These functions of calculus can be viewed as single-valued branches of curves in a coordinate system where the horizontal variable controls the vertical variable. In both studies the derivative multiplies incremental changes in the horizontal variable to yield incremental changes in the vertical variable and both studies possess the same rules of differentiation and integration. It seems that the two studies should be identical, that is, isomorphic. And, yet, students should be aware of important differences. In differential geometry, the horizontal and vertical units have the same dimensional units. In differential calculus the horizontal and vertical units are usually different, e.g., height vs. time. There are differences in the two studies with respect to the distance between points. In differential geometry, the Pythagorean slant distance formula prevails, while in the 2- dimensional plane of differential calculus there is no concept of slant distance. The derivative has a different meaning in each of the two subjects. In differential geometry, the slope of the tangent line determines the direction of the tangent line; that is, the angle with the horizontal axis. In differential calculus, there is no concept of direction; instead, the derivative describes a rate of change. In differential geometry the line described by the equation y = x subtends an angle, α, of 45° with the horizontal, but in calculus the linear relation, h = t, bears no concept of direction. -

Can One Design a Geometry Engine? on the (Un) Decidability of Affine
Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A. -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

Riemann's Contribution to Differential Geometry
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Historia Mathematics 9 (1982) l-18 RIEMANN'S CONTRIBUTION TO DIFFERENTIAL GEOMETRY BY ESTHER PORTNOY UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN, URBANA, IL 61801 SUMMARIES In order to make a reasonable assessment of the significance of Riemann's role in the history of dif- ferential geometry, not unduly influenced by his rep- utation as a great mathematician, we must examine the contents of his geometric writings and consider the response of other mathematicians in the years immedi- ately following their publication. Pour juger adkquatement le role de Riemann dans le developpement de la geometric differentielle sans etre influence outre mesure par sa reputation de trks grand mathematicien, nous devons &udier le contenu de ses travaux en geometric et prendre en consideration les reactions des autres mathematiciens au tours de trois an&es qui suivirent leur publication. Urn Riemann's Einfluss auf die Entwicklung der Differentialgeometrie richtig einzuschZtzen, ohne sich von seinem Ruf als bedeutender Mathematiker iiberm;issig beeindrucken zu lassen, ist es notwendig den Inhalt seiner geometrischen Schriften und die Haltung zeitgen&sischer Mathematiker unmittelbar nach ihrer Verijffentlichung zu untersuchen. On June 10, 1854, Georg Friedrich Bernhard Riemann read his probationary lecture, "iber die Hypothesen welche der Geometrie zu Grunde liegen," before the Philosophical Faculty at Gdttingen ill. His biographer, Dedekind [1892, 5491, reported that Riemann had worked hard to make the lecture understandable to nonmathematicians in the audience, and that the result was a masterpiece of presentation, in which the ideas were set forth clearly without the aid of analytic techniques. -

Riemannian Submanifolds: a Survey
RIEMANNIAN SUBMANIFOLDS: A SURVEY BANG-YEN CHEN Contents Chapter 1. Introduction .............................. ...................6 Chapter 2. Nash’s embedding theorem and some related results .........9 2.1. Cartan-Janet’s theorem .......................... ...............10 2.2. Nash’s embedding theorem ......................... .............11 2.3. Isometric immersions with the smallest possible codimension . 8 2.4. Isometric immersions with prescribed Gaussian or Gauss-Kronecker curvature .......................................... ..................12 2.5. Isometric immersions with prescribed mean curvature. ...........13 Chapter 3. Fundamental theorems, basic notions and results ...........14 3.1. Fundamental equations ........................... ..............14 3.2. Fundamental theorems ............................ ..............15 3.3. Basic notions ................................... ................16 3.4. A general inequality ............................. ...............17 3.5. Product immersions .............................. .............. 19 3.6. A relationship between k-Ricci tensor and shape operator . 20 3.7. Completeness of curvature surfaces . ..............22 Chapter 4. Rigidity and reduction theorems . ..............24 4.1. Rigidity ....................................... .................24 4.2. A reduction theorem .............................. ..............25 Chapter 5. Minimal submanifolds ....................... ...............26 arXiv:1307.1875v1 [math.DG] 7 Jul 2013 5.1. First and second variational formulas -

SOME GEOMETRY in HIGH-DIMENSIONAL SPACES 11 Containing Cn(S) Tends to ∞ with N
SOME GEOMETRY IN HIGH-DIMENSIONAL SPACES MATH 527A 1. Introduction Our geometric intuition is derived from three-dimensional space. Three coordinates suffice. Many objects of interest in analysis, however, require far more coordinates for a complete description. For example, a function f with domain [−1; 1] is defined by infinitely many \coordi- nates" f(t), one for each t 2 [−1; 1]. Or, we could consider f as being P1 n determined by its Taylor series n=0 ant (when such a representation exists). In that case, the numbers a0; a1; a2;::: could be thought of as coordinates. Perhaps the association of Fourier coefficients (there are countably many of them) to a periodic function is familiar; those are again coordinates of a sort. Strange Things can happen in infinite dimensions. One usually meets these, gradually (reluctantly?), in a course on Real Analysis or Func- tional Analysis. But infinite dimensional spaces need not always be completely mysterious; sometimes one lucks out and can watch a \coun- terintuitive" phenomenon developing in Rn for large n. This might be of use in one of several ways: perhaps the behavior for large but finite n is already useful, or one can deduce an interesting statement about limn!1 of something, or a peculiarity of infinite-dimensional spaces is illuminated. I will describe some curious features of cubes and balls in Rn, as n ! 1. These illustrate a phenomenon called concentration of measure. It will turn out that the important law of large numbers from probability theory is just one manifestation of high-dimensional geometry. -

Relativistic Spacetime Structure
Relativistic Spacetime Structure Samuel C. Fletcher∗ Department of Philosophy University of Minnesota, Twin Cities & Munich Center for Mathematical Philosophy Ludwig Maximilian University of Munich August 12, 2019 Abstract I survey from a modern perspective what spacetime structure there is according to the general theory of relativity, and what of it determines what else. I describe in some detail both the “standard” and various alternative answers to these questions. Besides bringing many underexplored topics to the attention of philosophers of physics and of science, metaphysicians of science, and foundationally minded physicists, I also aim to cast other, more familiar ones in a new light. 1 Introduction and Scope In the broadest sense, spacetime structure consists in the totality of relations between events and processes described in a spacetime theory, including distance, duration, motion, and (more gener- ally) change. A spacetime theory can attribute more or less such structure, and some parts of that structure may determine other parts. The nature of these structures and their relations of determi- nation bear on the interpretation of the theory—what the world would be like if the theory were true (North, 2009). For example, the structures of spacetime might be taken as its ontological or conceptual posits, and the determination relations might indicate which of these structures is more fundamental (North, 2018). Different perspectives on these questions might also reveal structural similarities with other spacetime theories, providing the resources to articulate how the picture of the world that that theory provides is different (if at all) from what came before, and might be different from what is yet to come.1 ∗Juliusz Doboszewski, Laurenz Hudetz, Eleanor Knox, J. -
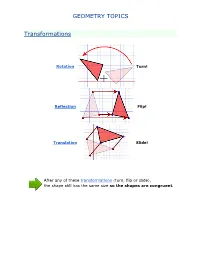
Geometry Topics
GEOMETRY TOPICS Transformations Rotation Turn! Reflection Flip! Translation Slide! After any of these transformations (turn, flip or slide), the shape still has the same size so the shapes are congruent. Rotations Rotation means turning around a center. The distance from the center to any point on the shape stays the same. The rotation has the same size as the original shape. Here a triangle is rotated around the point marked with a "+" Translations In Geometry, "Translation" simply means Moving. The translation has the same size of the original shape. To Translate a shape: Every point of the shape must move: the same distance in the same direction. Reflections A reflection is a flip over a line. In a Reflection every point is the same distance from a central line. The reflection has the same size as the original image. The central line is called the Mirror Line ... Mirror Lines can be in any direction. Reflection Symmetry Reflection Symmetry (sometimes called Line Symmetry or Mirror Symmetry) is easy to see, because one half is the reflection of the other half. Here my dog "Flame" has her face made perfectly symmetrical with a bit of photo magic. The white line down the center is the Line of Symmetry (also called the "Mirror Line") The reflection in this lake also has symmetry, but in this case: -The Line of Symmetry runs left-to-right (horizontally) -It is not perfect symmetry, because of the lake surface. Line of Symmetry The Line of Symmetry (also called the Mirror Line) can be in any direction. But there are four common directions, and they are named for the line they make on the standard XY graph. -

A CONCISE MINI HISTORY of GEOMETRY 1. Origin And
Kragujevac Journal of Mathematics Volume 38(1) (2014), Pages 5{21. A CONCISE MINI HISTORY OF GEOMETRY LEOPOLD VERSTRAELEN 1. Origin and development in Old Greece Mathematics was the crowning and lasting achievement of the ancient Greek cul- ture. To more or less extent, arithmetical and geometrical problems had been ex- plored already before, in several previous civilisations at various parts of the world, within a kind of practical mathematical scientific context. The knowledge which in particular as such first had been acquired in Mesopotamia and later on in Egypt, and the philosophical reflections on its meaning and its nature by \the Old Greeks", resulted in the sublime creation of mathematics as a characteristically abstract and deductive science. The name for this science, \mathematics", stems from the Greek language, and basically means \knowledge and understanding", and became of use in most other languages as well; realising however that, as a matter of fact, it is really an art to reach new knowledge and better understanding, the Dutch term for mathematics, \wiskunde", in translation: \the art to achieve wisdom", might be even more appropriate. For specimens of the human kind, \nature" essentially stands for their organised thoughts about sensations and perceptions of \their worlds outside and inside" and \doing mathematics" basically stands for their thoughtful living in \the universe" of their idealisations and abstractions of these sensations and perceptions. Or, as Stewart stated in the revised book \What is Mathematics?" of Courant and Robbins: \Mathematics links the abstract world of mental concepts to the real world of physical things without being located completely in either".