The Impact of Sea-Level Rise on Tidal Characteristics Around Australasia Alexander Harker1,2, J.A
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Australian Tidal Currents – Assessment of a Barotropic Model
https://doi.org/10.5194/gmd-2021-51 Preprint. Discussion started: 14 April 2021 c Author(s) 2021. CC BY 4.0 License. Australian tidal currents – assessment of a barotropic model (COMPAS v1.3.0 rev6631) with an unstructured grid. David A. Griffin1, Mike Herzfeld1, Mark Hemer1 and Darren Engwirda2 1Oceans and Atmosphere, CSIRO, Hobart, TAS 7000, Australia 2Center for Climate Systems Research, Columbia University, New York City, NY, USA and NASA Goddard Institute for 5 Space Studies, New York City, NY, USA Correspondence to: David Griffin ([email protected]) Abstract. While the variations of tidal range are large and fairly well known across Australia (less than 1 m near Perth but more than 14 m in King Sound), the properties of the tidal currents are not. We describe a new regional model of Australian 10 tides and assess it against a validation dataset comprising tidal height and velocity constituents at 615 tide gauge sites and 95 current meter sites. The model is a barotropic implementation of COMPAS, an unstructured-grid primitive-equation model that is forced at the open boundaries by TPXO9v1. The Mean Absolute value of the Error (MAE) of the modelled M2 height amplitude is 8.8 cm, or 12 % of the 73 cm mean observed amplitude. The MAE of phase (10°), however, is significant, so the M2 Mean Magnitude of Vector Error (MMVE, 18.2 cm) is significantly greater. The Root Sum Square over the 8 major 15 constituents is 26% of the observed amplitude.. We conclude that while the model has skill at height in all regions, there is definitely room for improvement (especially at some specific locations). -

The Impact of Sea-Level Rise on Tidal Characteristics Around Australia
The impact of sea-level rise on tidal characteristics around Australia ANGOR UNIVERSITY Harker, Alexander; Green, Mattias; Schindelegger, Michael; Wilmes, Sophie- Berenice Ocean Science DOI: 10.5194/os-2018-104 PRIFYSGOL BANGOR / B Published: 19/02/2019 Publisher's PDF, also known as Version of record Cyswllt i'r cyhoeddiad / Link to publication Dyfyniad o'r fersiwn a gyhoeddwyd / Citation for published version (APA): Harker, A., Green, M., Schindelegger, M., & Wilmes, S-B. (2019). The impact of sea-level rise on tidal characteristics around Australia. Ocean Science, 15(1), 147-159. https://doi.org/10.5194/os- 2018-104 Hawliau Cyffredinol / General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal ? Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. 07. Oct. 2021 Ocean Sci., 15, 147–159, 2019 https://doi.org/10.5194/os-15-147-2019 © Author(s) 2019. This work is distributed under the Creative Commons Attribution 4.0 License. -

In South Australia – Stock Structure and Adult Movement
SPATIAL MANAGEMENT OF SOUTHERN GARFISH (HYPORHAMPHUS MELANOCHIR) IN SOUTH AUSTRALIA – STOCK STRUCTURE AND ADULT MOVEMENT MA Steer, AJ Fowler, and BM Gillanders (Editors). Final Report for the Fisheries Research and Development Corporation FRDC Project No. 2007/029 SARDI Aquatic Sciences Publication No. F2009/000018-1 SARDI Research Report Series No. 333 ISBN 9781921563089 October 2009 i Title: Spatial management of southern garfish (Hyporhamphus melanochir) in South Australia – stock structure and adult movement Editors: MA Steer, AJ Fowler, and BM Gillanders. South Australian Research and Development Institute SARDI Aquatic Sciences 2 Hamra Avenue West Beach SA 5024 Telephone: (08) 8207 5400 Facsimile: (08) 8207 5406 http://www.sardi.sa.gov.au DISCLAIMER The authors do not warrant that the information in this document is free from errors or omissions. The authors do not accept any form of liability, be it contractual, tortious, or otherwise, for the contents of this document or for any consequences arising from its use or any reliance placed upon it. The information, opinions and advice contained in this document may not relate, or be relevant, to a readers particular circumstances. Opinions expressed by the authors are the individual opinions expressed by those persons and are not necessarily those of the publisher, research provider or the FRDC. © 2009 Fisheries Research and Development Corporation and SARDI Aquatic Sciences. This work is copyright. Apart from any use as permitted under the Copyright Act 1968 (Cwth), no part of this publication may be reproduced by any process, electronic or otherwise, without the specific written permission of the copyright owners. Neither may information be stored electronically in any form whatsoever without such permission. -

Permissive Residents: West Papuan Refugees Living in Papua New Guinea
Permissive residents West PaPuan refugees living in PaPua neW guinea Permissive residents West PaPuan refugees living in PaPua neW guinea Diana glazebrook MonograPhs in anthroPology series Published by ANU E Press The Australian National University Canberra ACT 0200, Australia Email: [email protected] This title is also available online at: http://epress.anu.edu.au/permissive_citation.html National Library of Australia Cataloguing-in-Publication entry Author: Glazebrook, Diana. Title: Permissive residents : West Papuan refugees living in Papua New Guinea / Diana Glazebrook. ISBN: 9781921536229 (pbk.) 9781921536236 (online) Subjects: Ethnology--Papua New Guinea--East Awin. Refugees--Papua New Guinea--East Awin. Refugees--Papua (Indonesia) Dewey Number: 305.8009953 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying or otherwise, without the prior permission of the publisher. Cover design by Teresa Prowse. Printed by University Printing Services, ANU This edition © 2008 ANU E Press Dedicated to the memory of Arnold Ap (1 July 1945 – 26 April 1984) and Marthen Rumabar (d. 2006). Table of Contents List of Illustrations ix Acknowledgements xi Glossary xiii Prologue 1 Intoxicating flag Chapter 1. Speaking historically about West Papua 13 Chapter 2. Culture as the conscious object of performance 31 Chapter 3. A flight path 51 Chapter 4. Sensing displacement 63 Chapter 5. Refugee settlements as social spaces 77 Chapter 6. Inscribing the empty rainforest with our history 85 Chapter 7. Unsated sago appetites 95 Chapter 8. Becoming translokal 107 Chapter 9. Permissive residents 117 Chapter 10. Relocation to connected places 131 Chapter 11. -

The Impact of Sea-Level Rise on Tidal Characteristics Around Australia Alexander Harker1,2, J
The impact of sea-level rise on tidal characteristics around Australia Alexander Harker1,2, J. A. Mattias Green2, Michael Schindelegger1, and Sophie-Berenice Wilmes2 1Institute of Geodesy and Geoinformation, University of Bonn, Bonn, Germany 2School of Ocean Sciences, Bangor University, Menai Bridge, United Kingdom Correspondence: Alexander Harker ([email protected]) Abstract. An established tidal model, validated for present-day conditions, is used to investigate the effect of large levels of sea-level rise (SLR) on tidal characteristics around Australasia. SLR is implemented through a uniform depth increase across the model domain, with a comparison between the implementation of coastal defences or allowing low-lying land to flood. The complex spatial response of the semi-diurnal M2 constituent does not appear to be linear with the imposed SLR. The most 5 predominant features of this response are the generation of new amphidromic systems within the Gulf of Carpentaria, and large amplitude changes in the Arafura Sea, to the north of Australia, and within embayments along Australia’s north-west coast. Dissipation from M2 notably decreases along north-west Australia, but is enhanced around New Zealand and the island chains to the north. The diurnal constituent, K1, is found to decrease in amplitude in the Gulf of Carpentaria when flooding is allowed. Coastal flooding has a profound impact on the response of tidal amplitudes to SLR by creating local regions of increased tidal 10 dissipation and altering the coastal topography. Our results also highlight the necessity for regional models to use correct open boundary conditions reflecting the global tidal changes in response to SLR. -

Marine Debris Survey Information Guide
Marine Debris Survey Information Guide Kristian Peters, Marine Debris Project Coordinator Adelaide and Mount Lofty Ranges Natural Resources Management Board Acknowledgements The Adelaide and Mount Lofty Ranges Natural Resources Management Board gratefully acknowledges the following contributors to this manual: • White, Damian. 2005. Marine Debris Survey Information Manual 2nd edition, WWF Marine Debris Project Arafura Ecoregion Program. WWF Australia • South Carolina Sea Grant Consortium • South Carolina Department of Health and Environmental Control Ocean and Coastal Resource Management • Centre for Ocean Sciences Education Excellence Southeast and NOAA 2008 • Chris Jordan • Images (cover from left): Kangaroo Island Natural Resources Management Board and Bill Doyle Photography This project is supported by the Adelaide and Mount Lofty Ranges Natural Resources Management Board through funding from the Australian Government’s Caring for our Country, the Whale and Dolphin Conservation Society and SeaLink. Disclaimer While every care is taken to ensure the accuracy of the information in this publication, the Adelaide and Mount Lofty Ranges Natural Resources Management Board takes no responsibility for its contents, nor for any loss, damage or consequence for any person or body relying on the information, or any error or omission in this publication. Printed on 100% recycled Australian-made paper from ISO 14001-accredited sources Marine Debris Survey Information Guide 1 Contents 1.0 Introduction ............................................................................................................................ -

Clockwise Phase Propagation of Semi-Diurnal Tides in the Gulf of Thailand
Journal of Oceanography, Vol. 54, pp. 143 to 150. 1998 Clockwise Phase Propagation of Semi-Diurnal Tides in the Gulf of Thailand 1 2 TETSUO YANAGI and TOSHIYUKI TAKAO 1Research Institute for Applied Mechanics, Kyushu University, Kasuga 816, Japan 2Department of Civil and Environmental Engineering, Ehime University, Matsuyama 790, Japan (Received 4 August 1997; in revised form 3 December 1997; accepted 6 December 1997) The phase of semi-diurnal tides (M and S ) propagates clockwise in the central part of Keywords: 2 2 ⋅ the Gulf of Thailand, although that of the diurnal tides (K1, O1 and P1) is counterclock- Clockwise wise. The mechanism of clockwise phase propagation of semi-diurnal tides at the Gulf of amphidrome, ⋅ natural oscillation, Thailand in the northern hemisphere is examined using a simple numerical model. The ⋅ natural oscillation period of the whole Gulf of Thailand is near the semi-diurnal period tide, ⋅ Gulf of Thailand. and the direction of its phase propagation is clockwise, mainly due to the propagation direction of the large amplitude part of the incoming semi-diurnal tidal wave from the South China Sea. A simplified basin model with bottom slope and Coriolis force well reproduces the co-tidal and co-range charts of M2 tide in the Gulf of Thailand. 1. Introduction phase propagation of semi-diurnal tides at the Gulf of It is well known that the phase of tides propagates Thailand in the northern hemisphere using a simple numeri- counterclockwise (clockwise) in gulfs or shelf seas such as cal model. the North Sea, the Baltic, the Adria, the Persian Gulf, the Yellow Sea, the Sea of Okhotsk, the Gulf of Mexico and so 2. -

Lecture 1: Introduction to Ocean Tides
Lecture 1: Introduction to ocean tides Myrl Hendershott 1 Introduction The phenomenon of oceanic tides has been observed and studied by humanity for centuries. Success in localized tidal prediction and in the general understanding of tidal propagation in ocean basins led to the belief that this was a well understood phenomenon and no longer of interest for scientific investigation. However, recent decades have seen a renewal of interest for this subject by the scientific community. The goal is now to understand the dissipation of tidal energy in the ocean. Research done in the seventies suggested that rather than being mostly dissipated on continental shelves and shallow seas, tidal energy could excite far traveling internal waves in the ocean. Through interaction with oceanic currents, topographic features or with other waves, these could transfer energy to smaller scales and contribute to oceanic mixing. This has been suggested as a possible driving mechanism for the thermohaline circulation. This first lecture is introductory and its aim is to review the tidal generating mechanisms and to arrive at a mathematical expression for the tide generating potential. 2 Tide Generating Forces Tidal oscillations are the response of the ocean and the Earth to the gravitational pull of celestial bodies other than the Earth. Because of their movement relative to the Earth, this gravitational pull changes in time, and because of the finite size of the Earth, it also varies in space over its surface. Fortunately for local tidal prediction, the temporal response of the ocean is very linear, allowing tidal records to be interpreted as the superposition of periodic components with frequencies associated with the movements of the celestial bodies exerting the force. -
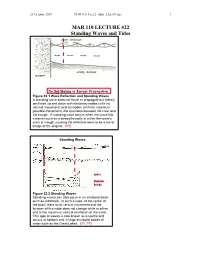
MAR 110 LECTURE #22 Standing Waves and Tides
23 October 2007 MAR110_Lec22_tides_23oct07.doc 1 MAR 110 LECTURE #22 Standing Waves and Tides No Net Motion or Energy Propagation Figure 22.1 Wave Reflection and Standing Waves A standing wave does not travel or propagate but merely oscillates up and down with stationary nodes (with no vertical movement) and antinodes (with the maximum possible movement) that oscillates between the crest and the trough. A standing wave occurs when the wave hits a barrier such as a seawall exactly at either the wave’s crest or trough, causing the reflected wave to be a mirror image of the original. (??) Standing Waves and a Bathtub Seiche Figure 22.2 Standing Waves Standing waves can also occur in an enclosed basin such as a bathtub. In such a case, at the center of the basin there is no vertical movement and the location of this node does not change while at either end is the maximum vertical oscillation of the water. This type of waves is also known as a seiche and occurs in harbors and in large enclosed bodies of water such as the Great Lakes. (??, ??) 23 October 2007 MAR110_Lec22_tides_23oct07.doc 2 Standing Wave or Seiche Period l Figure 22.3 The wavelength of a standing wave is equal to twice the length of the basin it is in, which along with the depth (d) of the water within the basin, determines the period (T) of the wave. (ItO) Standing Waves & Bay Tides l Figure 22.4 Another type of standing wave occurs in an open basin that has a length (l) one quarter that of the wave in this case, usually a tide. -

Conserving Marine Biodiversity in South Australia - Part 1 - Background, Status and Review of Approach to Marine Biodiversity Conservation in South Australia
Conserving Marine Biodiversity in South Australia - Part 1 - Background, Status and Review of Approach to Marine Biodiversity Conservation in South Australia K S Edyvane May 1999 ISBN 0 7308 5237 7 No 38 The recommendations given in this publication are based on the best available information at the time of writing. The South Australian Research and Development Institute (SARDI) makes no warranty of any kind expressed or implied concerning the use of technology mentioned in this publication. © SARDI. This work is copyright. Apart of any use as permitted under the Copyright Act 1968, no part may be reproduced by any process without prior written permission from the publisher. SARDI is a group of the Department of Primary Industries and Resources CONTENTS – PART ONE PAGE CONTENTS NUMBER INTRODUCTION 1. Introduction…………………………………..…………………………………………………………1 1.1 The ‘Unique South’ – Southern Australia’s Temperate Marine Biota…………………………….…….1 1.2 1.2 The Status of Marine Protected Areas in Southern Australia………………………………….4 2 South Australia’s Marine Ecosystems and Biodiversity……………………………………………..9 2.1 Oceans, Gulfs and Estuaries – South Australia’s Oceanographic Environments……………………….9 2.1.1 Productivity…………………………………………………………………………………….9 2.1.2 Estuaries………………………………………………………………………………………..9 2.2 Rocky Cliffs and Gulfs, to Mangrove Shores -South Australia’s Coastal Environments………………………………………………………………13 2.2.1 Offshore Islands………………………………………………………………………………14 2.2.2 Gulf Ecosystems………………………………………………………………………………14 2.2.3 Northern Spencer Gulf………………………………………………………………………...14 -

A Precious Asset
Gulf St Vincent A PRECIOUS ASSET Gulf St Vincent A PRECIOUS AssET Introduction It is more than 70 years since Since that time, the Gulf has We need these people, and other William Light sailed up the eastern provided safe, reliable transport for members of the Gulf community, side of Gulf St Vincent, looking for most of our produce and material to share their knowledge, to the entrance to a harbour which needs, as well as fresh fish, coastal make all users of the Gulf aware had been reported by the explorer, living, recreation and inspiration. of its value, its benefits and its Captain Collet Barker, and the In return we have muddied its vulnerability. It is time for us all to whaling captain, John Jones. waters with stormwater, effluent learn more about Gulf St Vincent, He found waters calm and clear and industrial wastes, bulldozed to recognise the priceless asset enough to avoid shoals and to its dunes, locked up sand under we have, and to do our utmost to safely anchor through the spring houses and greedily exploited its reverse the trail of destruction we gales blowing from the south-west. marine life. Just reflect a moment have left in the last 00 years. Perhaps even he saw sea eagles on what Adelaide in particular, and The more we know of the Gulf, fishing or nesting in the low trees South Australia as a whole, would its physical nature and marine life, and bushes on the dunes, which be like without Gulf St Vincent, to the more readily we recognise extended along the coast from realise the importance of the Gulf the threats posed by increasing Brighton to the Port River. -

Causes of Tides – Tutorial Script in the First Video Tutorial of This Series, We Studied Tidal Data from Many Locations Worldwide and Learned How Tides Behave
Causes of Tides – Tutorial Script In the first video tutorial of this series, we studied tidal data from many locations worldwide and learned how tides behave. In this video tutorial, we will explore the causes of that behavior. First of all, we know that most tidal waves have a period of one wave every 12 hrs and 25 minutes otherwise stated as two waves every 24 hrs and 50 minutes. What else has that same period? Earth’s rotation relative to the Moon is also 24 hours and 50 minutes. What does that mean? After the Earth has rotated once relative to the Sun – 24 hours – it has to rotate another 50 minutes to catch up with the Moon, which during that 24 hours moved 1/29th its way around its orbit around the Earth. 24 hours and 50 minutes is a lunar day. In addition, the two week cycle of neap and spring tides exactly matches the phases of the Moon as the Moon completes its orbit around the Earth. The Moon is the main agent causing tides on our planet. How? This image, which is not to scale, shows a spherical blue Earth that is being pulled to the right by a gravitational force between itself and the Moon. The side of Earth closest to the Moon has a longer arrow, representing the stronger gravitational force felt there. The arrow on the opposite side is shorter because its force is smaller. Gravitational force is stronger, the closer two objects are together and weaker, the further away they are.