Pattern Speed of Lopsidedness in Galactic Disks
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

THE 1000 BRIGHTEST HIPASS GALAXIES: H I PROPERTIES B
The Astronomical Journal, 128:16–46, 2004 July A # 2004. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE 1000 BRIGHTEST HIPASS GALAXIES: H i PROPERTIES B. S. Koribalski,1 L. Staveley-Smith,1 V. A. Kilborn,1, 2 S. D. Ryder,3 R. C. Kraan-Korteweg,4 E. V. Ryan-Weber,1, 5 R. D. Ekers,1 H. Jerjen,6 P. A. Henning,7 M. E. Putman,8 M. A. Zwaan,5, 9 W. J. G. de Blok,1,10 M. R. Calabretta,1 M. J. Disney,10 R. F. Minchin,10 R. Bhathal,11 P. J. Boyce,10 M. J. Drinkwater,12 K. C. Freeman,6 B. K. Gibson,2 A. J. Green,13 R. F. Haynes,1 S. Juraszek,13 M. J. Kesteven,1 P. M. Knezek,14 S. Mader,1 M. Marquarding,1 M. Meyer,5 J. R. Mould,15 T. Oosterloo,16 J. O’Brien,1,6 R. M. Price,7 E. M. Sadler,13 A. Schro¨der,17 I. M. Stewart,17 F. Stootman,11 M. Waugh,1, 5 B. E. Warren,1, 6 R. L. Webster,5 and A. E. Wright1 Received 2002 October 30; accepted 2004 April 7 ABSTRACT We present the HIPASS Bright Galaxy Catalog (BGC), which contains the 1000 H i brightest galaxies in the southern sky as obtained from the H i Parkes All-Sky Survey (HIPASS). The selection of the brightest sources is basedontheirHi peak flux density (Speak k116 mJy) as measured from the spatially integrated HIPASS spectrum. 7 ; 10 The derived H i masses range from 10 to 4 10 M . -

Dust and CO Emission Towards the Centers of Normal Galaxies, Starburst Galaxies and Active Galactic Nuclei�,�� I
A&A 462, 575–579 (2007) Astronomy DOI: 10.1051/0004-6361:20047017 & c ESO 2007 Astrophysics Dust and CO emission towards the centers of normal galaxies, starburst galaxies and active galactic nuclei, I. New data and updated catalogue M. Albrecht1,E.Krügel2, and R. Chini3 1 Instituto de Astronomía, Universidad Católica del Norte, Avenida Angamos 0610, Antofagasta, Chile e-mail: [email protected] 2 Max-Planck-Institut für Radioastronomie (MPIfR), Auf dem Hügel 69, 53121 Bonn, Germany 3 Astronomisches Institut der Ruhr-Universität Bochum (AIRUB), Universitätsstr. 150 NA7, 44780 Bochum, Germany Received 6 January 2004 / Accepted 27 October 2006 ABSTRACT Aims. The amount of interstellar matter in a galaxy determines its evolution, star formation rate and the activity phenomena in the nucleus. We therefore aimed at obtaining a data base of the 12CO line and thermal dust emission within equal beamsizes for galaxies in a variety of activity stages. Methods. We have conducted a search for the 12CO (1–0) and (2–1) transitions and the continuum emission at 1300 µmtowardsthe centers of 88 galaxies using the IRAM 30 m telescope (MRT) and the Swedish ESO Submillimeter Telescope (SEST). The galaxies > are selected to be bright in the far infrared (S 100 µm ∼ 9 Jy) and optically fairly compact (D25 ≤ 180 ). We have applied optical spectroscopy and IRAS colours to group the galaxies of the entire sample according to their stage of activity into three sub-samples: normal, starburst and active galactic nuclei (AGN). The continuum emission has been corrected for line contamination and synchrotron contribution to retrieve the thermal dust emission. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -
![Arxiv:1803.01321V1 [Astro-Ph.GA] 4 Mar 2018 H Adsget Rw” Uhrte Ogand Calling Long Feature, Rather Such This “Rows”](https://docslib.b-cdn.net/cover/9532/arxiv-1803-01321v1-astro-ph-ga-4-mar-2018-h-adsget-rw-uhrte-ogand-calling-long-feature-rather-such-this-rows-1569532.webp)
Arxiv:1803.01321V1 [Astro-Ph.GA] 4 Mar 2018 H Adsget Rw” Uhrte Ogand Calling Long Feature, Rather Such This “Rows”
Butenko M.A., Khoperskov A.V. Galaxies with https://doi.org/10.1134/S1990341317030130 “Rows”: A New Catalog // Astrophysical Bul- letin, 2017, vol.72, No.3, 232–250 GALAXIES WITH “ROWS”: A NEW CATALOG M. A. Butenko1, * and A. V. Khoperskov1, ** 1Volgograd State University, Volgograd, 400062 Russia Galaxies with “rows” in Vorontsov-Velyaminov’s terminology stand out among the variety of spiral galactic patterns. A characteristic feature of such objects is the sequence of straight- line segments that forms the spiral arm. In 2001 A. Chernin and co-authors published a catalog of such galaxies which includes 204 objects from the Palomar Atlas. In this paper, we supplement the catalog with 276 objects based on an analysis of all the galaxies from the New General Catalogue and Index Catalogue. The total number of NGC and IC galaxies with rows is 406, including the objects of Chernin et al. (2001). The use of more recent galaxy images allowed us to detect more “rows” on average, compared with the catalog of Chernin et al. When comparing the principal galaxy properties we found no significant differences between galaxies with rows and all S-typeNGC/IC galaxies.We discuss twomechanisms for the formation of polygonal structures based on numerical gas-dynamic and collisionless N- body calculations, which demonstrate that a spiral pattern with rows is a transient stage in the evolution of galaxies and a system with a powerful spiral structure can pass through this stage. The hypothesis of A. Chernin et al. (2001) that the occurrence frequency of interacting galaxies is twice higher among galaxies with rows is not confirmed for the combined set of 480 galaxies. -

Bar Strength and Star Formation Activity in Late-Type Barred Galaxies
A&A manuscript no. (will be inserted by hand later) ASTRONOMY AND Your thesaurus codes are: ASTROPHYSICS 4(11.01.1; 11.05.2; 11.19.3; 13.09.1) 30.9.2018 Bar strength and star formation activity in late-type barred galaxies L. Martinet and D. Friedli ⋆ Observatoire de Gen`eve, CH-1290 Sauverny, Switzerland E-mail: [email protected] Received 23 September 1996 / Accepted 24 December 1996 Abstract. With the prime aim of better probing and un- the past. For instance, the role of gas, the effects of inter- derstanding the intimate link between star formation ac- actions not only between galaxies but also between vari- tivity and the presence of bars, a representative sample of ous components of a given system, the necessity to fully 32 non-interacting late-type galaxies with well-determined take into account 3D structures, the interplay between bar properties has been selected. We show that all the star formation and dynamical mechanisms, etc. In fact, galaxies displaying the highest current star forming ac- discs are the seat of evolutionary processes on timescales tivity have both strong and long bars. Conversely not all of the order of the Hubble time or less (see the reviews by strong and long bars are intensively creating stars. Except Kormendy 1982; Martinet 1995; Pfenniger 1996; see also for two cases, strong bars are in fact long as well. Numer- e.g. Pfenniger & Norman 1990; Friedli & Benz 1993, 1995; ical simulations allow to understand these observational Courteau et al. 1996; Norman et al. 1996). In particular, facts as well as the connection between bar axis ratio, bars do play a decisive role in such processes. -

Nuclear Activity in Circumnuclear Ring Galaxies
International Journal of Astronomy and Astrophysics, 2016, 6, 219-235 Published Online September 2016 in SciRes. http://www.scirp.org/journal/ijaa http://dx.doi.org/10.4236/ijaa.2016.63018 Nuclear Activity in Circumnuclear Ring Galaxies María P. Agüero1, Rubén J. Díaz2,3, Horacio Dottori4 1Observatorio Astronómico de Córdoba, UNCand CONICET, Córdoba, Argentina 2ICATE, CONICET, San Juan, Argentina 3Gemini Observatory, La Serena, Chile 4Instituto de Física, UFRGS, Porto Alegre, Brazil Received 23 May 2016; accepted 26 July 2016; published 29 July 2016 Copyright © 2016 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract We have analyzed the frequency and properties of the nuclear activity in a sample of galaxies with circumnuclear rings and spirals (CNRs), compiled from published data. From the properties of this sample a typical circumnuclear ring can be characterized as having a median radius of 0.7 kpc (mean 0.8 kpc, rms 0.4 kpc), located at a spiral Sa/Sb galaxy (75% of the hosts), with a bar (44% weak, 37% strong bars). The sample includes 73 emission line rings, 12 dust rings and 9 stellar rings. The sample was compared with a carefully matched control sample of galaxies with very similar global properties but without detected circumnuclear rings. We discuss the relevance of the results in regard to the AGN feeding processes and present the following results: 1) bright companion galaxies seem -

Characterizing the V-Band Light-Curves of Hydrogen-Rich Type Ii Supernovae∗
The Astrophysical Journal, 786:67 (35pp), 2014 May 1 doi:10.1088/0004-637X/786/1/67 C 2014. The American Astronomical Society. All rights reserved. Printed in the U.S.A. CHARACTERIZING THE V-BAND LIGHT-CURVES OF HYDROGEN-RICH TYPE II SUPERNOVAE∗ Joseph P. Anderson1,2, Santiago Gonzalez-Gait´ an´ 1, Mario Hamuy1,3, Claudia P. Gutierrez´ 1,3, Maximilian D. Stritzinger4, Felipe Olivares E.5, Mark M. Phillips6, Steve Schulze7, Roberto Antezana1, Luis Bolt8, Abdo Campillay6, Sergio Castellon´ 6, Carlos Contreras4, Thomas de Jaeger1,3,Gaston´ Folatelli9, Francisco Forster¨ 1, Wendy L. Freedman10, Luis Gonzalez´ 1, Eric Hsiao6, Wojtek Krzeminski´ 11, Kevin Krisciunas12, Jose´ Maza1, Patrick McCarthy10, Nidia I. Morrell6, Sven E. Persson10, Miguel Roth6, Francisco Salgado13, Nicholas B. Suntzeff12, and Joanna Thomas-Osip6 1 Departamento de Astronom´ıa, Universidad de Chile, Casilla 36-D, Santiago, Chile; [email protected] 2 European Southern Observatory, Alonso de Cordova 3107, Vitacura, Santiago, Chile 3 Millennium Institute of Astrophysics, Casilla 36-D, Santiago, Chile 4 Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, DK-8000 Aarhus C, Denmark 5 Departamento de Ciencias Fisicas, Universidad Andres Bello, Avda. Republica 252, Santiago, Chile 6 Carnegie Observatories, Las Campanas Observatory, Casilla 601, La Serena, Chile 7 Instituto de Astrof´ısica, Facultad de F´ısica, Pontif´ıcia Universidad Catolica´ de Chile, Casilla 306, Santiago 22, Chile 8 Argelander Institut fur¨ Astronomie, Universitat¨ Bonn, Auf dem Hugel¨ 71, D-53111 Bonn, Germany 9 Institute for the Physics and Mathematics of the Universe (IPMU), University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba 277-8583, Japan 10 Observatories of the Carnegie Institution for Science, Pasadena, CA 91101, USA 11 N. -
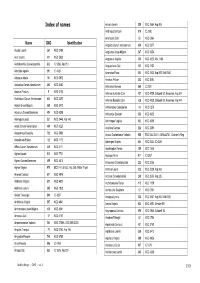
190 Index of Names
Index of names Ancora Leonis 389 NGC 3664, Arp 005 Andriscus Centauri 879 IC 3290 Anemodes Ceti 85 NGC 0864 Name CMG Identification Angelica Canum Venaticorum 659 NGC 5377 Accola Leonis 367 NGC 3489 Angulatus Ursae Majoris 247 NGC 2654 Acer Leonis 411 NGC 3832 Angulosus Virginis 450 NGC 4123, Mrk 1466 Acritobrachius Camelopardalis 833 IC 0356, Arp 213 Angusticlavia Ceti 102 NGC 1032 Actenista Apodis 891 IC 4633 Anomalus Piscis 804 NGC 7603, Arp 092, Mrk 0530 Actuosus Arietis 95 NGC 0972 Ansatus Antliae 303 NGC 3084 Aculeatus Canum Venaticorum 460 NGC 4183 Antarctica Mensae 865 IC 2051 Aculeus Piscium 9 NGC 0100 Antenna Australis Corvi 437 NGC 4039, Caldwell 61, Antennae, Arp 244 Acutifolium Canum Venaticorum 650 NGC 5297 Antenna Borealis Corvi 436 NGC 4038, Caldwell 60, Antennae, Arp 244 Adelus Ursae Majoris 668 NGC 5473 Anthemodes Cassiopeiae 34 NGC 0278 Adversus Comae Berenices 484 NGC 4298 Anticampe Centauri 550 NGC 4622 Aeluropus Lyncis 231 NGC 2445, Arp 143 Antirrhopus Virginis 532 NGC 4550 Aeola Canum Venaticorum 469 NGC 4220 Anulifera Carinae 226 NGC 2381 Aequanimus Draconis 705 NGC 5905 Anulus Grahamianus Volantis 955 ESO 034-IG011, AM0644-741, Graham's Ring Aequilibrata Eridani 122 NGC 1172 Aphenges Virginis 654 NGC 5334, IC 4338 Affinis Canum Venaticorum 449 NGC 4111 Apostrophus Fornac 159 NGC 1406 Agiton Aquarii 812 NGC 7721 Aquilops Gruis 911 IC 5267 Aglaea Comae Berenices 489 NGC 4314 Araneosus Camelopardalis 223 NGC 2336 Agrius Virginis 975 MCG -01-30-033, Arp 248, Wild's Triplet Aratrum Leonis 323 NGC 3239, Arp 263 Ahenea -

Making a Sky Atlas
Appendix A Making a Sky Atlas Although a number of very advanced sky atlases are now available in print, none is likely to be ideal for any given task. Published atlases will probably have too few or too many guide stars, too few or too many deep-sky objects plotted in them, wrong- size charts, etc. I found that with MegaStar I could design and make, specifically for my survey, a “just right” personalized atlas. My atlas consists of 108 charts, each about twenty square degrees in size, with guide stars down to magnitude 8.9. I used only the northernmost 78 charts, since I observed the sky only down to –35°. On the charts I plotted only the objects I wanted to observe. In addition I made enlargements of small, overcrowded areas (“quad charts”) as well as separate large-scale charts for the Virgo Galaxy Cluster, the latter with guide stars down to magnitude 11.4. I put the charts in plastic sheet protectors in a three-ring binder, taking them out and plac- ing them on my telescope mount’s clipboard as needed. To find an object I would use the 35 mm finder (except in the Virgo Cluster, where I used the 60 mm as the finder) to point the ensemble of telescopes at the indicated spot among the guide stars. If the object was not seen in the 35 mm, as it usually was not, I would then look in the larger telescopes. If the object was not immediately visible even in the primary telescope – a not uncommon occur- rence due to inexact initial pointing – I would then scan around for it. -

Astrofotografie Beobachtungstipps Koordinatensysteme
April 2018 € 2,50 Astrofotografie Beobachtungstipps Koordinatensysteme ISSN 1618-6362 Entfernungsbestimmung Orion- und Pferdekopfnebel sowie Staubregionen im Orion am 30./31. 12. 2016 von Thomas Winterer in Geigersau aufgenommen mit Canon EF 80-200 mm f/4 bei 135 mm und Offen- blende, QSI 683 WS-8, Ha-RGB 120/30/30/30 Min, hier jedoch nur der H-alpha Anteil (siehe auch das Astrofoto in der Heftmitte). Herausgegeben von der Astronomischen Vereinigung Augsburg e.V. Öffnungszeiten der Sternwarte Diedorf: Freitag ab 20 Uhr Heft 90, April 2018 Liebe Leserin, lieber Leser, sich die Zukunft auszumalen macht INHALT Freude. Inspirationen kann man sich Entfernungsbestimmung offener Sternhaufen 4 leicht bei Science-Fiction Filmen holen. Ein Selbstversuch mit Amateurmitteln Doch nicht nur Filme, auch Bücher kön- Urgroßvaters Weltraumfahrt 8 nen einen Leser fesseln. Einer meiner Als das All leer war - Blicke in die Zukunft von anno dazumal spannendsten Scifi-Romane handelte vom Wettlauf zwischen Amerikanern Einstieg in die bunte Welt der Astrofotografie 11 und Chinesen zur Ausbeutung von Heli- Ein Erfahrungsbericht um-3 auf dem Mond, um die Energiepro- Space Art bleme auf der Erde zu lösen. Das Buch 16 Projekte von Michael Böhme „Limit“ von Frank Schätzing hat über 1300 Seiten, doch wenn man sich die er- Wie funktionieren astronomische Koordinatensysteme? 18 sten 200 Seiten erarbeitet hat, lässt ei- Grundlagen der Himmelsmechanik nen die packende Geschichte nicht mehr los. Orion und Pferdekopfnebel 20 Als Jugendlicher hatte ich schon ein Astrofoto großes Interesse an zukünftigen tech- ‘Oumuamua 22 nischen Entwicklungen, und ich war des- Ein Reisender zwischen den Sternen halb Abonnent der Zeitschrift „hobby“. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

A Mid-Infrared Study of Dust Emission from Core-Collapse Supernovae
UNIVERSITY COLLEGE LONDON Faculty of Mathematics and Physical Sciences Department of Physics & Astronomy A MID-INFRARED STUDY OF DUST EMISSION FROM CORE-COLLAPSE SUPERNOVAE Thesis submitted for the Degree of Doctor of Philosophy of the University of London by Joanna Natalina Fabbri Supervisors: Examiners: Prof. Michael J. Barlow Prof. Stephen Eales Prof. Jonathan M. C. Rawlings Dr. Serena Viti May 13, 2011 To my family and friends, without whom this journey would not have been possible. Declaration I, Joanna Natalina Fabbri, confirm that the work presented in this thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the thesis. “Share your knowledge. It is a way to achieve immortality.” – The Dalai Lama “I don’t want to achieve immortality through my work... ...I want to achieve it through not dying.” – Woody Allen Abstract The aim of this thesis has been to help elucidate the potential contribution of core-collapse supernovae (SNe) to the dust-enrichment of galaxies. It has long been hypothesised that SNe are a major source of dust in the Universe, an assumption that has gained support with the discovery that many of the earliest-formed galaxies are extremely dusty and infrared- luminous, as evidenced by the efficient detection of their redshifted infrared emission at submillimeter wavelengths. Massive-star, core-collapse SNe, of Types II, Ib and Ic, arising from the starbursts that power these galaxies, are plausible sources of this dust. However, very little is currently known about how much dust forms in SN outflows. To this end, sensitive mid-infrared surveys for thermal dust emission from recent core-collapse SNe have been conducted with the Spitzer Space Telescope and mid-infrared detectors on the Gemini telescopes, in order to seek evidence for dust formation and evolution in SN ejecta.