Study on Raffenetti's P File Format in Conventional Ab Initio Self-Consistent-Field Molecular Orbital Calculations in Parallel
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

GABA Receptors
D Reviews • BIOTREND Reviews • BIOTREND Reviews • BIOTREND Reviews • BIOTREND Reviews Review No.7 / 1-2011 GABA receptors Wolfgang Froestl , CNS & Chemistry Expert, AC Immune SA, PSE Building B - EPFL, CH-1015 Lausanne, Phone: +41 21 693 91 43, FAX: +41 21 693 91 20, E-mail: [email protected] GABA Activation of the GABA A receptor leads to an influx of chloride GABA ( -aminobutyric acid; Figure 1) is the most important and ions and to a hyperpolarization of the membrane. 16 subunits with γ most abundant inhibitory neurotransmitter in the mammalian molecular weights between 50 and 65 kD have been identified brain 1,2 , where it was first discovered in 1950 3-5 . It is a small achiral so far, 6 subunits, 3 subunits, 3 subunits, and the , , α β γ δ ε θ molecule with molecular weight of 103 g/mol and high water solu - and subunits 8,9 . π bility. At 25°C one gram of water can dissolve 1.3 grams of GABA. 2 Such a hydrophilic molecule (log P = -2.13, PSA = 63.3 Å ) cannot In the meantime all GABA A receptor binding sites have been eluci - cross the blood brain barrier. It is produced in the brain by decarb- dated in great detail. The GABA site is located at the interface oxylation of L-glutamic acid by the enzyme glutamic acid decarb- between and subunits. Benzodiazepines interact with subunit α β oxylase (GAD, EC 4.1.1.15). It is a neutral amino acid with pK = combinations ( ) ( ) , which is the most abundant combi - 1 α1 2 β2 2 γ2 4.23 and pK = 10.43. -

)&F1y3x PHARMACEUTICAL APPENDIX to THE
)&f1y3X PHARMACEUTICAL APPENDIX TO THE HARMONIZED TARIFF SCHEDULE )&f1y3X PHARMACEUTICAL APPENDIX TO THE TARIFF SCHEDULE 3 Table 1. This table enumerates products described by International Non-proprietary Names (INN) which shall be entered free of duty under general note 13 to the tariff schedule. The Chemical Abstracts Service (CAS) registry numbers also set forth in this table are included to assist in the identification of the products concerned. For purposes of the tariff schedule, any references to a product enumerated in this table includes such product by whatever name known. Product CAS No. Product CAS No. ABAMECTIN 65195-55-3 ACTODIGIN 36983-69-4 ABANOQUIL 90402-40-7 ADAFENOXATE 82168-26-1 ABCIXIMAB 143653-53-6 ADAMEXINE 54785-02-3 ABECARNIL 111841-85-1 ADAPALENE 106685-40-9 ABITESARTAN 137882-98-5 ADAPROLOL 101479-70-3 ABLUKAST 96566-25-5 ADATANSERIN 127266-56-2 ABUNIDAZOLE 91017-58-2 ADEFOVIR 106941-25-7 ACADESINE 2627-69-2 ADELMIDROL 1675-66-7 ACAMPROSATE 77337-76-9 ADEMETIONINE 17176-17-9 ACAPRAZINE 55485-20-6 ADENOSINE PHOSPHATE 61-19-8 ACARBOSE 56180-94-0 ADIBENDAN 100510-33-6 ACEBROCHOL 514-50-1 ADICILLIN 525-94-0 ACEBURIC ACID 26976-72-7 ADIMOLOL 78459-19-5 ACEBUTOLOL 37517-30-9 ADINAZOLAM 37115-32-5 ACECAINIDE 32795-44-1 ADIPHENINE 64-95-9 ACECARBROMAL 77-66-7 ADIPIODONE 606-17-7 ACECLIDINE 827-61-2 ADITEREN 56066-19-4 ACECLOFENAC 89796-99-6 ADITOPRIM 56066-63-8 ACEDAPSONE 77-46-3 ADOSOPINE 88124-26-9 ACEDIASULFONE SODIUM 127-60-6 ADOZELESIN 110314-48-2 ACEDOBEN 556-08-1 ADRAFINIL 63547-13-7 ACEFLURANOL 80595-73-9 ADRENALONE -
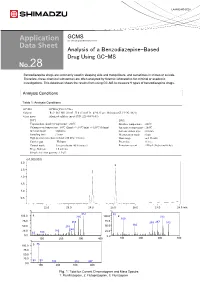
Analysis of a Benzodiazepine-Based Drug Using GC-MS 28
LAAN-E-MS-E028 GCMS Gas Chromatograph Mass Spectrometer Analysis of a Benzodiazepine-Based Drug Using GC-MS 28 Benzodiazepine drugs are commonly used in sleeping aids and tranquilizers, and sometimes in crimes or suicide. Therefore, these chemical substances are often analyzed by forensic laboratories for criminal or academic investigations. This datasheet shows the results from using GC-MS to measure 9 types of benzodiazepine drugs. Analysis Conditions Table 1: Analysis Conditions GC-MS :GCMS-QP2010 Ultra Column : Rxi®-5Sil MS (30 mL. X 0.25 mmI.D., df=0.25 µm, Shimadzu GLC P/N:13623) Glass insert :Silanized splitless insert (P/N: 221-48876-03) [GC] [MS] Vaporization chamber temperature : 260℃ Interface temperature : 280℃ Column oven temperature : 60℃ (2min) -> (10℃/min) -> 320℃ (10min) Ion source temperature : 200℃ Injection mode : Splitless Solvent elution time : 2.0 min Sampling time : 1 min Measurement mode : Scan High pressure injection method: 250 kPa (1.5 min) Mass range : m/z 35-600 Carrier gas : Helium Event time : 0.3 sec Control mode :Linear velocity (45.6 cm/sec) Emission current : 150 µA (high sensitivity) Purge flow rate :3.0 ml/min Sample injection quantity :1.0 µL (x1,000,000) 3.0 3 2.5 2 2.0 1.5 1.0 1 0.5 22.0 23.0 24.0 25.0 26.0 27.0 28.0 min % % 312 55 100.0 1 285 100.0 2 313 109 75.0 75.0 266 259287 342 166 50.0 238 50.0 248 25.0 183 25.0 63 109 0.0 0.0 100 200 300 400 100 200 300 400 % 86 100.0 3 75.0 50.0 25.0 58 99 183 315 387 0.0 100 200 300 400 Fig. -

Statistical Analysis Plan Statistical Center for HIV/AIDS Research & SCHARP Prevention SD Standard Deviation SI International System of Units
67$7,67,&$/$1$/<6,63/$1 $:((.)/(;,%/('26(23(1/$%(/ 08/7,&(17(5(;7(16,21678'<72(9$/8$7(7+( /21*7(506$)(7<$1'())(&7,9(1(662) /85$6,'21(,13(',$75,&68%-(&76 /XUDVLGRQH60/DWXGD 6WXG\1R' 9HUVLRQ1XPEHU)LQDO 9HUVLRQ'DWH1RY $XWKRUL]DWLRQ6LJQDWXUH3DJH $:((.)/(;,%/('26(23(1/$%(/08/7,&(17(5(;7(16,21 678'<72(9$/8$7(7+(/21*7(506$)(7<$1'())(&7,9(1(662) /85$6,'21(,13(',$75,&68%-(&76 $XWKRU 1DPH 'DWH 3RVLWLRQ6HQLRU 'LUHFWRU%LRVWDWLVWLFV &RPSDQ\6XQRYLRQ3KDUPDFHXWLFDOV,QF $SSURYHGE\ 1DPH 'DWH 3RVLWLRQ 6HQLRU'LUHFWRU&OLQLFDO'HYHORSPHQW DQG0HGLFDO$IIDLUV&16 &RPSDQ\6XQRYLRQ3KDUPDFHXWLFDOV,QF 1DPH 'DWH 3RVLWLRQ([HFXWLYH'LUHFWRU%LRVWDWLVWLFV &RPSDQ\6XQRYLRQ3KDUPDFHXWLFDOV,QF Table of contents 1. INTRODUCTION ........................................................................................................9 1.1. Study Objectives ...........................................................................................................9 1.2. Study Design ...............................................................................................................10 1.2.1. Determination of Sample Size ....................................................................................11 1.2.2. Randomization and Blinding ......................................................................................11 2. ANALYSES PLANNED ............................................................................................12 2.1. General Analysis Definition .......................................................................................12 2.1.1. Logic -

(12) Patent Application Publication (10) Pub. No.: US 2009/0005722 A1 Jennings-Spring (43) Pub
US 20090005722A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2009/0005722 A1 Jennings-Spring (43) Pub. Date: Jan. 1, 2009 (54) SKIN-CONTACTING-ADHESIVE FREE Publication Classification DRESSING (51) Int. Cl. Inventor: Barbara Jennings-Spring, Jupiter, A61N L/30 (2006.01) (76) A6F I3/00 (2006.01) FL (US) A6IL I5/00 (2006.01) Correspondence Address: AOIG 7/06 (2006.01) Irving M. Fishman AOIG 7/04 (2006.01) c/o Cohen, Tauber, Spievack and Wagner (52) U.S. Cl. .................. 604/20: 602/43: 602/48; 4771.5; Suite 2400, 420 Lexington Avenue 47/13 New York, NY 10170 (US) (57) ABSTRACT (21) Appl. No.: 12/231,104 A dressing having a flexible sleeve shaped to accommodate a Substantially cylindrical body portion, the sleeve having a (22) Filed: Aug. 29, 2008 lining which is substantially non-adherent to the body part being bandaged and having a peripheral securement means Related U.S. Application Data which attaches two peripheral portions to each other without (63) Continuation-in-part of application No. 1 1/434,689, those portions being circumferentially adhered to the sleeve filed on May 16, 2006. portion. Patent Application Publication Jan. 1, 2009 Sheet 1 of 9 US 2009/0005722 A1 Patent Application Publication Jan. 1, 2009 Sheet 2 of 9 US 2009/0005722 A1 10 8 F.G. 5 Patent Application Publication Jan. 1, 2009 Sheet 3 of 9 US 2009/0005722 A1 13 FIG.6 2 - Y TIII Till "T fift 11 10 FIG.7 8 13 6 - 12 - Timir" "in "in "MINIII. -

Drug and Medication Classification Schedule
KENTUCKY HORSE RACING COMMISSION UNIFORM DRUG, MEDICATION, AND SUBSTANCE CLASSIFICATION SCHEDULE KHRC 8-020-1 (11/2018) Class A drugs, medications, and substances are those (1) that have the highest potential to influence performance in the equine athlete, regardless of their approval by the United States Food and Drug Administration, or (2) that lack approval by the United States Food and Drug Administration but have pharmacologic effects similar to certain Class B drugs, medications, or substances that are approved by the United States Food and Drug Administration. Acecarbromal Bolasterone Cimaterol Divalproex Fluanisone Acetophenazine Boldione Citalopram Dixyrazine Fludiazepam Adinazolam Brimondine Cllibucaine Donepezil Flunitrazepam Alcuronium Bromazepam Clobazam Dopamine Fluopromazine Alfentanil Bromfenac Clocapramine Doxacurium Fluoresone Almotriptan Bromisovalum Clomethiazole Doxapram Fluoxetine Alphaprodine Bromocriptine Clomipramine Doxazosin Flupenthixol Alpidem Bromperidol Clonazepam Doxefazepam Flupirtine Alprazolam Brotizolam Clorazepate Doxepin Flurazepam Alprenolol Bufexamac Clormecaine Droperidol Fluspirilene Althesin Bupivacaine Clostebol Duloxetine Flutoprazepam Aminorex Buprenorphine Clothiapine Eletriptan Fluvoxamine Amisulpride Buspirone Clotiazepam Enalapril Formebolone Amitriptyline Bupropion Cloxazolam Enciprazine Fosinopril Amobarbital Butabartital Clozapine Endorphins Furzabol Amoxapine Butacaine Cobratoxin Enkephalins Galantamine Amperozide Butalbital Cocaine Ephedrine Gallamine Amphetamine Butanilicaine Codeine -

Report on the Investigation Results
Pharmaceuticals and Medical Devices Agency This English version is intended to be a reference material to provide convenience for users. In the event of inconsistency between the Japanese original and this English translation, the former shall prevail. Report on the Investigation Results February 28, 2017 Pharmaceuticals and Medical Devices Agency I. Overview of Product [Non-proprietary name] See Attachment 1 [Brand name] See Attachment 1 [Approval holder] See Attachment 1 [Indications] See Attachment 1 [Dosage and administration] See Attachment 1 [Investigating office] Office of Safety II 1 Pharmaceuticals and Medical Devices Agency This English version is intended to be a reference material to provide convenience for users. In the event of inconsistency between the Japanese original and this English translation, the former shall prevail. II. Background of the investigation 1. Status in Japan Hypnotics and anxiolytics are prescribed by various specialties and widely used in clinical practice. In particular, benzodiazepine (BZ) receptor agonists, which act on BZ receptors, bind to gamma-aminobutyric acid (GABA)A-BZ receptor complex and enhance the function of GABAA receptors. This promotes neurotransmission of inhibitory systems and demonstrates hypnotic/sedative effects, anxiolytic effects, muscle relaxant effects, and antispasmodic effects. Since the approval of chlordiazepoxide in March 1961, many BZ receptor agonists have been approved as hypnotics and anxiolytics. Currently, hypnotics and anxiolytics are causative agents of drug-related disorders such as drug dependence in Japanese clinical practice. Hypnotics and anxiolitics that rank high in causative agents are BZ receptor agonists for which high frequencies of high doses and multidrug prescriptions have been reported (Japanese Journal of Clinical Psychopharmacology 2013; 16(6): 803-812, Modern Physician 2014; 34(6): 653-656, etc.). -

Bioanalytical Studies of Designer Benzodiazepines
From DEPARTMENT OF LABORATORY MEDICINE Karolinska Institutet, Stockholm, Sweden BIOANALYTICAL STUDIES OF DESIGNER BENZODIAZEPINES Madeleine Pettersson Bergstrand Stockholm 2018 All previously published papers were reproduced with permission from the publisher. Published by Karolinska Institutet. Printed by Eprint AB © Madeleine Pettersson Bergstrand, 2018 ISBN 978-91-7831-063-0 Front page illustration: Sandra Eriksson Bioanalytical studies of designer benzodiazepines THESIS FOR DOCTORAL DEGREE (Ph.D.) The thesis will be defended at 4X, Alfred Nobels allé 8, Huddinge Friday, May 25, 2018 at 09.00 a.m. By Madeleine Pettersson Bergstrand Principal Supervisor: Opponent: Prof. Anders Helander Ass. Prof. Elisabeth Leere Øiestad Karolinska Institutet Oslo University Hospital Department of Laboratory Medicine Department of Forensic Sciences Division of Clinical Chemistry Clinic for Laboratory medicine Co-supervisor: Examination Board: Prof. Olof Beck Prof. Åsa Emmer Karolinska Institutet KTH Royal Institute of Technology Department of Laboratory Medicine Department of Chemistry Division of Clinical Pharmacology Division of Applied Physical Chemistry Docent Stefan Borg Karolinska Institutet Department of Clinical Neuroscience Docent Pierre Lafolie Karolinska Institutet Department of Medicine Division of Clinical Epidemiology ABSTRACT The fast appearance of benzodiazepine analogues, referred to as new psychoactive substance (NPS) or designer benzodiazepines, requires the continuous update of detection methods in order to keep up with the latest drugs on the recreational drug market. Moreover, as usually only limited information on toxicity and excretion patterns of these new drugs exists, this needs to be evaluated to report on adverse effects and to determine suitable targets for drug testing. Urine drug testing usually involves screening using immunoassay followed by confirmation of positive screening results using mass spectrometric (MS) methods. -

A Review of the Evidence of Use and Harms of Novel Benzodiazepines
ACMD Advisory Council on the Misuse of Drugs Novel Benzodiazepines A review of the evidence of use and harms of Novel Benzodiazepines April 2020 1 Contents 1. Introduction ................................................................................................................................. 4 2. Legal control of benzodiazepines .......................................................................................... 4 3. Benzodiazepine chemistry and pharmacology .................................................................. 6 4. Benzodiazepine misuse............................................................................................................ 7 Benzodiazepine use with opioids ................................................................................................... 9 Social harms of benzodiazepine use .......................................................................................... 10 Suicide ............................................................................................................................................. 11 5. Prevalence and harm summaries of Novel Benzodiazepines ...................................... 11 1. Flualprazolam ......................................................................................................................... 11 2. Norfludiazepam ....................................................................................................................... 13 3. Flunitrazolam .......................................................................................................................... -

II.3.4 Benzodiazepines by Hiroshi Seno and Hideki Hattori
3.4 II.3.4 Benzodiazepines by Hiroshi Seno and Hideki Hattori Introduction Benzodiazepines show antianxiety, hypnotic, anticonvulsant and muscle-relaxant eff ects. Th is group of drugs has wide safety dose ranges; it means that the ratio of the LD50 to the ED50 (therapeutic index) is high. Because of its safety, benzodiazepines are being widely used in the world. Some of benzodiazepines are also being abused or used for so-called “ drug facilitated sexual assault”, and thus they are under the control of the Narcotics and Psychotropics Control Law; in Japan, triazolam abuse has become one of the serious social problems. In this chapter, a GC/MS method for simultaneous analysis of 22 kinds of benzodiazepines listed in > Table 4.1 is described. In addition, the LC/MS analysis of triazolam, and its metabolites 4-hydroxy- triazolam and α-hydroxytriazolam is also presented. GC/MS analysis of benzodiazepines in blood and urine Reagents and their preparation • Th e pure powder of the 22 kinds of benzodiazepines was donated by each pharmaceutical manufacturers according to the authors’ request a (some of benzodiazepines now obtaina- ble from Sigma, St. Louis, MO, USA). • 1 M Sodium bicarbonate solution: a 8.4-g aliquot of sodium bicarbonate is dissolved in distilled water to prepare 100 mL solution. • 2 M Sodium acetate solution: a 27.5-g aliquot of sodium acetate is dissolved in distilled water to prepare 100 mL solution. GC/MS conditions Column: a DB-5 fused silica capillary column (30 m × 0.25 mm i.d., fi lm thickness 0.25 µm, J & W Scientifi c, Folsom, CA, USA). -

Muscle Relaxants for Pain Management in Rheumatoid Arthritis (Review)
Muscle relaxants for pain management in rheumatoid arthritis (Review) Richards BL, Whittle SL, Buchbinder R This is a reprint of a Cochrane review, prepared and maintained by The Cochrane Collaboration and published in The Cochrane Library 2012, Issue 1 http://www.thecochranelibrary.com Muscle relaxants for pain management in rheumatoid arthritis (Review) Copyright © 2012 The Cochrane Collaboration. Published by John Wiley & Sons, Ltd. TABLE OF CONTENTS HEADER....................................... 1 ABSTRACT ...................................... 1 PLAINLANGUAGESUMMARY . 2 SUMMARY OF FINDINGS FOR THE MAIN COMPARISON . ..... 3 BACKGROUND .................................... 6 OBJECTIVES ..................................... 7 METHODS ...................................... 7 RESULTS....................................... 10 Figure1. ..................................... 11 Figure2. ..................................... 13 Figure3. ..................................... 15 Figure4. ..................................... 15 Figure5. ..................................... 16 Figure6. ..................................... 17 Figure7. ..................................... 17 Figure8. ..................................... 18 DISCUSSION ..................................... 20 AUTHORS’CONCLUSIONS . 21 ACKNOWLEDGEMENTS . 22 REFERENCES ..................................... 22 CHARACTERISTICSOFSTUDIES . 24 DATAANDANALYSES. 35 Analysis 1.1. Comparison 1 Muscle relaxant versus control, Outcome 1 Pain 24hrs. 37 Analysis 1.2. Comparison 1 Muscle relaxant -

Federal Register / Vol. 60, No. 80 / Wednesday, April 26, 1995 / Notices DIX to the HTSUS—Continued
20558 Federal Register / Vol. 60, No. 80 / Wednesday, April 26, 1995 / Notices DEPARMENT OF THE TREASURY Services, U.S. Customs Service, 1301 TABLE 1.ÐPHARMACEUTICAL APPEN- Constitution Avenue NW, Washington, DIX TO THE HTSUSÐContinued Customs Service D.C. 20229 at (202) 927±1060. CAS No. Pharmaceutical [T.D. 95±33] Dated: April 14, 1995. 52±78±8 ..................... NORETHANDROLONE. A. W. Tennant, 52±86±8 ..................... HALOPERIDOL. Pharmaceutical Tables 1 and 3 of the Director, Office of Laboratories and Scientific 52±88±0 ..................... ATROPINE METHONITRATE. HTSUS 52±90±4 ..................... CYSTEINE. Services. 53±03±2 ..................... PREDNISONE. 53±06±5 ..................... CORTISONE. AGENCY: Customs Service, Department TABLE 1.ÐPHARMACEUTICAL 53±10±1 ..................... HYDROXYDIONE SODIUM SUCCI- of the Treasury. NATE. APPENDIX TO THE HTSUS 53±16±7 ..................... ESTRONE. ACTION: Listing of the products found in 53±18±9 ..................... BIETASERPINE. Table 1 and Table 3 of the CAS No. Pharmaceutical 53±19±0 ..................... MITOTANE. 53±31±6 ..................... MEDIBAZINE. Pharmaceutical Appendix to the N/A ............................. ACTAGARDIN. 53±33±8 ..................... PARAMETHASONE. Harmonized Tariff Schedule of the N/A ............................. ARDACIN. 53±34±9 ..................... FLUPREDNISOLONE. N/A ............................. BICIROMAB. 53±39±4 ..................... OXANDROLONE. United States of America in Chemical N/A ............................. CELUCLORAL. 53±43±0