DOCSLIB.ORG

COMPUTATIONAL MODELLING of PROTEIN FIBRILLATION with APPLICATION to GLUCAGON Hamed Tabatabaei Ghomi Purdue University

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
COMPUTATIONAL MODELLING of PROTEIN FIBRILLATION with APPLICATION to GLUCAGON Hamed Tabatabaei Ghomi Purdue University Purdue University Purdue e-Pubs Open Access Dissertations Theses and Dissertations January 2015 COMPUTATIONAL MODELLING OF PROTEIN FIBRILLATION WITH APPLICATION TO GLUCAGON Hamed Tabatabaei Ghomi Purdue University Follow this and additional works at: https://docs.lib.purdue.edu/open_access_dissertations Recommended Citation Tabatabaei Ghomi, Hamed, "COMPUTATIONAL MODELLING OF PROTEIN FIBRILLATION WITH APPLICATION TO GLUCAGON" (2015). Open Access Dissertations. 1321. https://docs.lib.purdue.edu/open_access_dissertations/1321 This document has been made available through Purdue e-Pubs, a service of the Purdue University Libraries. Please contact [email protected] for additional information. i COMPUTATIONAL MODELLING OF PROTEIN FIBRILLATION WITH APPLICATION TO GLUCAGON A Dissertation Submitted to the Faculty of Purdue University by Hamed Tabatabaei Ghomi In Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy i December 2015 Purdue University West Lafayette, Indiana ii ای الهه ای رتاهن ام آشیاهن ام یس ای ربای شاد ز تن بهاهن ام قهرمان قصه اهی عاشقاهن ام نس با یم انم تو بهار می شود بذر شعراهی اتزه رد میان خاک بی رقار می شود ii iii ACKNOWLEDGEMENTS I am indebted to my advisors, Dr. Lill and Dr. Topp who taught me many things about science, and about life. Also, I thank my advisory committee, Dr. Park, Dr. Post and Dr. Kihara for all their support. I am grateful to my lovely wife, Elaheh. I owe all my success to her support and sacrifice. I am also grateful to my parent for their support and encouragement. And finally, I owe my deepest and greatest gratitude to God, the Most Beneficent, the Most Merciful. iii iv TABLE OF CONTENTS Page LIST OF TABLES ........................................................................................................... viii LIST OF FIGURES ........................................................................................................... ix ABSTRACT ..................................................................................................................... xvi CHAPTER 1. INTRODUCTION .................................................................................... 1 1.1 Computational Modelling of Amyloid Fibrils .......................................................... 1 1.2 Glucagon Fibrillation ................................................................................................ 2 1.3 Outline ....................................................................................................................... 3 CHAPTER 2. PENTAPEPTIDE CHAPERONES TO INHIBIT GLUCAGON FIBRILLATION ................................................................................................................. 4 2.1 Introduction ............................................................................................................... 4 2.2 Materials and methods .............................................................................................. 4 2.2.1 Peptide design .................................................................................................. 4 2.2.2 Sample Preparation .......................................................................................... 7 2.2.3 ThT Assay ........................................................................................................ 8 2.2.4 Intrinsic Fluorescence Assay ........................................................................... 8 2.2.5 Partial Least Square Regression ...................................................................... 8 2.2.6 MD Simulations ............................................................................................... 9 iv 2.3 Results ..................................................................................................................... 11 2.3.1 Glucagon interactions by MD simulation ...................................................... 11 2.3.2 Glucagon Fibrillation ..................................................................................... 15 2.3.3 Fibrillation lag time extension ....................................................................... 16 2.3.4 PLS model ..................................................................................................... 25 2.4 Conclusions ............................................................................................................. 25 v Page CHAPTER 3. ARE DISTANCE-DEPENDENT STATISTICAL POTENTIALS CONSIDERING THREE INTERACTING BODIES SUPERIOR TO TWO-BODY STATISTICAL POTENTIALS FOR PROTEIN STRUCTURE PREDICTION? .......... 30 3.1 Introduction ............................................................................................................. 30 3.2 Materials and Methods ............................................................................................ 34 3.2.1 Assigning the properties to proteins .............................................................. 34 3.2.2 Protein database for generation of statistical potential .................................. 35 3.2.3 Interacting Pairs and Triplets ......................................................................... 35 3.2.4 Statistical potential and definition of reference state ..................................... 37 3.2.5 Smoothed Potential ........................................................................................ 39 3.2.6 Scoring ........................................................................................................... 39 3.2.7 Other scoring functions used for comparison ................................................ 39 3.2.7.1 Simple Counting Methods ........................................................................ 40 3.2.7.2 Conventional Scoring Functions .............................................................. 40 3.2.8 Decoy Sets ..................................................................................................... 43 3.3 Results and Discussions .......................................................................................... 46 3.3.1 Quasi-three-body pseudo-potentials .............................................................. 46 3.3.2 Quasi-three-body scoring functions ............................................................... 49 3.3.3 Correlations between different scoring functions .......................................... 51 v 3.4 Conclusion ............................................................................................................... 88 CHAPTER 4. FIBPREDICTOR: A COMPUTATIONAL METHOD FOR RAPID PREDICTION OF AMYLOID -FIBRIL STRUCTURES ............................................. 93 4.1 Introduction ............................................................................................................. 93 4.2 Materials and Methods ............................................................................................ 94 4.2.1 Input for Fibpredictor .................................................................................... 94 4.2.2 Generating the structural ensemble ............................................................... 94 4.2.3 Scoring the ensemble structures .................................................................... 96 4.2.4 FibPredictor usage and GUI .......................................................................... 97 4.2.4.1 Sequences of the first and the second sheets: ........................................... 97 vi Page 4.2.4.2 Sense of the β-sheets: ............................................................................... 98 4.2.4.3 Scoring function: ...................................................................................... 98 4.2.4.4 Rotations: .................................................................................................. 98 4.2.4.5 Number of randomly generated models (Rand. models): ......................... 98 4.2.4.6 Top models: .............................................................................................. 99 4.2.4.7 Minimum distance between the sheets: .................................................... 99 4.2.4.8 Distance variation between the sheets: ..................................................... 99 4.2.4.9 Angle variation between the sheets: ......................................................... 99 4.2.5 Validation ...................................................................................................... 99 4.3 Results and discussion ........................................................................................... 105 4.4 Conclusions ........................................................................................................... 122 CHAPTER 5. PHOSPHATE ESTER DERIVATIVES OF GLUCAGON ................. 124 5.1 Introduction ........................................................................................................... 124 5.2 Materials and Methods .......................................................................................... 124 5.2.1 Phosphorylation Sites and Possible Phospho-glucagon Prodrugs ............... 124 5.2.2 Computational Modelling of Glucagon Fibrils ............................................ 125 5.2.3 MD Simulations ........................................................................................... 126 5.2.4 Peptides and their solubility......................................................................... 128 5.2.5 Stability study (24 h) ................................................................................... 128 vi 5.2.6 Initial stability
Load more

Recommended publications
  • Annual Scientific Report 2013 on the Cover Structure 3Fof in the Protein Data Bank, Determined by Laponogov, I
    EMBL-European Bioinformatics Institute Annual Scientific Report 2013 On the cover Structure 3fof in the Protein Data Bank, determined by Laponogov, I. et al. (2009) Structural insight into the quinolone-DNA cleavage complex of type IIA topoisomerases. Nature Structural & Molecular Biology 16, 667-669. © 2014 European Molecular Biology Laboratory This publication was produced by the External Relations team at the European Bioinformatics Institute (EMBL-EBI) A digital version of the brochure can be found at www.ebi.ac.uk/about/brochures For more information about EMBL-EBI please contact: [email protected] Contents Introduction & overview 3 Services 8 Genes, genomes and variation 8 Molecular atlas 12 Proteins and protein families 14 Molecular and cellular structures 18 Chemical biology 20 Molecular systems 22 Cross-domain tools and resources 24 Research 26 Support 32 ELIXIR 36 Facts and figures 38 Funding & resource allocation 38 Growth of core resources 40 Collaborations 42 Our staff in 2013 44 Scientific advisory committees 46 Major database collaborations 50 Publications 52 Organisation of EMBL-EBI leadership 61 2013 EMBL-EBI Annual Scientific Report 1 Foreword Welcome to EMBL-EBI’s 2013 Annual Scientific Report. Here we look back on our major achievements during the year, reflecting on the delivery of our world-class services, research, training, industry collaboration and European coordination of life-science data. The past year has been one full of exciting changes, both scientifically and organisationally. We unveiled a new website that helps users explore our resources more seamlessly, saw the publication of ground-breaking work in data storage and synthetic biology, joined the global alliance for global health, built important new relationships with our partners in industry and celebrated the launch of ELIXIR.
    [Show full text]
  • Roles of Nickel Binding Proteins in Helicobacter Species
    ROLES OF NICKEL BINDING PROTEINS IN HELICOBACTER SPECIES by SUSMITHA SESHADRI (Under the Direction of Robert J. Maier) ABSTRACT Proteins Hpn and Hpn-like of the gastric pathogen H. pylori were hypothesized to bind nickel since histidine residues make up 45% and 27% of their amino acid content, respectively. Characterization of an hpn, an hpn-like and an hpn, hpn-like double mutant revealed novel functions for these gene products in nickel detoxification and storage. Compared to the wild-type parent, mutant strains were more sensitive to elevated concentrations of nickel, cobalt, and cadmium, indicating roles for the two proteins in surviving metal toxicity. Under low nickel conditions, the mutants exhibited higher urease activities and had increased amount of Ni- associated with urease; but similar urease apo-protein levels to wild-type. The parent achieved mutant level urease activities under nickel supplementation and lower pH conditions while growth with a nickel chelator decreased mutant but not wild-type urease activities. These results strongly imply a role for these proteins as nickel reservoirs/storage proteins. H. hepaticus colonizes a non-acidic niche, hence nickel metabolism may be different than in H. pylori. A nikR mutant exhibited higher urease and hydrogenase activities under all supplemental nickel conditions, but there was no change in urease expression, and NikR did not bind pUreA or pHydA. Higher total nickel levels (detected by ICP-MS) in the nikR mutant implied possible higher nickel transporter (NikA) levels, which was later verified by qRT-PCR and binding of NikR to pNikA. Periplasmic nitrate reductase (NapA) was upregulated in the NikR strain.
    [Show full text]
  • A Highly Accurate Model for Screening Prostate Cancer Using Propensity Index Panel of Ten Genes
    bioRxiv preprint doi: https://doi.org/10.1101/2021.03.22.436371; this version posted March 22, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY 4.0 International license. A highly accurate model for screening prostate cancer using propensity index panel of ten genes Shipra Jain#, Kawal Preet Kaur Malhotra#, Sumeet Patiyal#, Gajendra P. S. Raghava* Department of Computational Biology, Indraprastha Institute of Information Technology, New Delhi-110020, India. # - Contributed Equally * - Corresponding Author Mailing Address of Authors Shipra Jain: [email protected] ORCID ID: https://orcid.org/0000-0002-7045-5188 Kawal Preet Kaur Malhotra: [email protected] Sumeet Patiyal: [email protected] ORCID ID: https://orcid.org/0000-0003-1358-292X GPS Raghava: [email protected] ORCID ID: https://orcid.org/0000-0002-8902-2876 Corresponding Author Gajendra Pal Singh Raghava Head and Professor, Department of Computational Biology Office: A-302 R&D Block, Indraprastha Institute of Information Technology, Delhi Okhla Industrial Estate, Phase III, (Near Govind Puri Metro Station) New Delhi, India - 110020 Phone: 011-26907444 Email: [email protected] Website: http://webs.iiitd.edu.in/raghava/ Highlights ● Application of Machine learning techniques to identify Biomarkers for PRAD cancer. ● Highly accurate models developed for classifying prostate cancer vs. normal sample. ● Introducing Propensity index concept for enhancing model performance. ● Top 10 genes identified using feature selection techniques. bioRxiv preprint doi: https://doi.org/10.1101/2021.03.22.436371; this version posted March 22, 2021.
    [Show full text]
  • The Human Genome Project
    TO KNOW OURSELVES ❖ THE U.S. DEPARTMENT OF ENERGY AND THE HUMAN GENOME PROJECT JULY 1996 TO KNOW OURSELVES ❖ THE U.S. DEPARTMENT OF ENERGY AND THE HUMAN GENOME PROJECT JULY 1996 Contents FOREWORD . 2 THE GENOME PROJECT—WHY THE DOE? . 4 A bold but logical step INTRODUCING THE HUMAN GENOME . 6 The recipe for life Some definitions . 6 A plan of action . 8 EXPLORING THE GENOMIC LANDSCAPE . 10 Mapping the terrain Two giant steps: Chromosomes 16 and 19 . 12 Getting down to details: Sequencing the genome . 16 Shotguns and transposons . 20 How good is good enough? . 26 Sidebar: Tools of the Trade . 17 Sidebar: The Mighty Mouse . 24 BEYOND BIOLOGY . 27 Instrumentation and informatics Smaller is better—And other developments . 27 Dealing with the data . 30 ETHICAL, LEGAL, AND SOCIAL IMPLICATIONS . 32 An essential dimension of genome research Foreword T THE END OF THE ROAD in Little has been rapid, and it is now generally agreed Cottonwood Canyon, near Salt that this international project will produce Lake City, Alta is a place of the complete sequence of the human genome near-mythic renown among by the year 2005. A skiers. In time it may well And what is more important, the value assume similar status among molecular of the project also appears beyond doubt. geneticists. In December 1984, a conference Genome research is revolutionizing biology there, co-sponsored by the U.S. Department and biotechnology, and providing a vital of Energy, pondered a single question: Does thrust to the increasingly broad scope of the modern DNA research offer a way of detect- biological sciences.
    [Show full text]
  • Complex Rearrangement of Chromosomes 19, 21, and 22 In
    Cancer Genetics and Cytogenetics 181 (2008) 81e92 Complex rearrangement of chromosomes 19, 21, and 22 in Ewing sarcoma involving a novel reciprocal inversioneinsertion mechanism of EWSeERG fusion gene formation: a case analysis and literature review Georges Mairea, Christopher W. Brownb,c,d, Jane Bayania, Carlos Pereirae, Denis H. Gravelf, John C. Bellc, Maria Zielenskae,g,h, Jeremy A. Squirea,h* aDivision of Applied Molecular Oncology, Ontario Cancer Institute, Princess Margaret Hospital, University Health Network, 610 University Avenue, Room 9-717, Toronto, Ontario M5G 2M9, Canada bOttawa Health Research Institute, Centre for Cancer Therapeutics, Ottawa, Ontario, Canada cDepartment of Biochemistry, Microbiology and Immunology, University of Ottawa, Ottawa, Ontario, Canada dDepartment of Orthopaedic Surgery, Ottawa Hospital and University of Ottawa, Ottawa, Ontario, Canada eDepartment of Pediatric Laboratory Medicine and Pathology, The Hospital for Sick Children, Toronto, Ontario, Canada fDepartment of Pathology and Laboratory Medicine, Ottawa Hospital and University of Ottawa, Ottawa, Ontario, Canada gGenetics and Genome Biology, Hospital for Sick Children, Toronto, Ontario, Canada hDepartment of Laboratory Medicine and Pathology, University of Toronto, Toronto, Ontario, Canada Received 9 August 2007; received in revised form 5 November 2007; accepted 7 November 2007 Abstract EWSeERG Ewing sarcoma (ES) gene fusions often result from complex chromosomal rearrange- ments. We report an unusually aggressive case of ES with an EWSeERG fusion gene that appeared to be a result of a simple balanced and reciprocal translocation, t(19;22)(q13.2;q12.2). Subsequent molecular investigation of the primary tumor, the metastasis, and a cell line generated from this ES permitted reconstruction of each genomic step in the evolution of this complex EWSeERG fusion.
    [Show full text]
  • S41419-021-03972-6.Pdf
    www.nature.com/cddis ARTICLE OPEN Primed to die: an investigation of the genetic mechanisms underlying noise-induced hearing loss and cochlear damage in homozygous Foxo3-knockout mice ✉ Holly J. Beaulac1,3, Felicia Gilels1,4, Jingyuan Zhang1,5, Sarah Jeoung2 and Patricia M. White 1 © The Author(s) 2021 The prevalence of noise-induced hearing loss (NIHL) continues to increase, with limited therapies available for individuals with cochlear damage. We have previously established that the transcription factor FOXO3 is necessary to preserve outer hair cells (OHCs) and hearing thresholds up to two weeks following mild noise exposure in mice. The mechanisms by which FOXO3 preserves cochlear cells and function are unknown. In this study, we analyzed the immediate effects of mild noise exposure on wild-type, Foxo3 heterozygous (Foxo3+/−), and Foxo3 knock-out (Foxo3−/−) mice to better understand FOXO3’s role(s) in the mammalian cochlea. We used confocal and multiphoton microscopy to examine well-characterized components of noise-induced damage including calcium regulators, oxidative stress, necrosis, and caspase-dependent and caspase-independent apoptosis. Lower immunoreactivity of the calcium buffer Oncomodulin in Foxo3−/− OHCs correlated with cell loss beginning 4 h post-noise exposure. Using immunohistochemistry, we identified parthanatos as the cell death pathway for OHCs. Oxidative stress response pathways were not significantly altered in FOXO3’s absence. We used RNA sequencing to identify and RT-qPCR to confirm differentially expressed genes. We further investigated a gene downregulated in the unexposed Foxo3−/− mice that may contribute to OHC noise susceptibility. Glycerophosphodiester phosphodiesterase domain containing 3 (GDPD3), a possible endogenous source of lysophosphatidic acid (LPA), has not previously been described in the cochlea.
    [Show full text]
  • Mouse Hpn Knockout Project (CRISPR/Cas9)
    https://www.alphaknockout.com Mouse Hpn Knockout Project (CRISPR/Cas9) Objective: To create a Hpn knockout Mouse model (C57BL/6J) by CRISPR/Cas-mediated genome engineering. Strategy summary: The Hpn gene (NCBI Reference Sequence: NM_001110252 ; Ensembl: ENSMUSG00000001249 ) is located on Mouse chromosome 7. 14 exons are identified, with the ATG start codon in exon 2 and the TGA stop codon in exon 14 (Transcript: ENSMUST00000108102). Exon 2~5 will be selected as target site. Cas9 and gRNA will be co-injected into fertilized eggs for KO Mouse production. The pups will be genotyped by PCR followed by sequencing analysis. Note: Mice homozygous for a null mutation are hypothyroidic and develop profound hearing loss associated with structural changes in the tectorial membrane and a myelination defect affecting the compaction of spiral ganglion neurons. Exon 2 starts from the coding region. Exon 2~5 covers 16.59% of the coding region. The size of effective KO region: ~5780 bp. The KO region does not have any other known gene. Page 1 of 9 https://www.alphaknockout.com Overview of the Targeting Strategy Wildtype allele 5' gRNA region gRNA region 3' 1 2 3 4 5 14 Legends Exon of mouse Hpn Knockout region Page 2 of 9 https://www.alphaknockout.com Overview of the Dot Plot (up) Window size: 15 bp Forward Reverse Complement Sequence 12 Note: The 391 bp section upstream of Exon 2 is aligned with itself to determine if there are tandem repeats. No significant tandem repeat is found in the dot plot matrix. So this region is suitable for PCR screening or sequencing analysis.
    [Show full text]
  • Protein Preliminaries and Structure Prediction Fundamentals For
    AN ARXIV PREPRINT 1 Protein preliminaries and structure prediction fundamentals for computer scientists Mahmood A. Rashid, Firas Khatib, and Abdul Sattar Abstract—Protein structure prediction is a chal- I. PROTEIN FUNDAMENTALS lenging and unsolved problem in computer science. Proteins are the sequence of amino acids connected Proteins are the principal constituents of the together by single peptide bond. The combinations of protoplasm of all cells. Proteins essentially con- the twenty primary amino acids are the constituents sist of amino acids, which are themselves bonded of all proteins. In-vitro laboratory methods used in by peptide linkages. In this section, we give an this problem are very time-consuming, cost-intensive, overview of protein preliminaries. and failure-prone. Thus, alternative computational methods come into play. The protein structure predic- tion problem is to find the three-dimensional native A. Amino acids structure of a protein, from its amino acid sequence. The native structure of a protein has the minimum Amino acids, also known as protein monomers free energy possible and arguably determines the or residues, are the molecules containing an amino function of the protein. In this study, we present the group, a carboxyl group, and a side-chain. This preliminaries of proteins and their structures, protein side-chain is the only component that varies be- structure prediction problem, and protein models. We tween different amino acids. Figure 1 shows the also give a brief overview on experimental and compu- tational methods used in protein structure prediction. generic structure of an amino acid. An amino This study will provide a fundamental knowledge to acid has the generic formula H2NCHROOH.
    [Show full text]
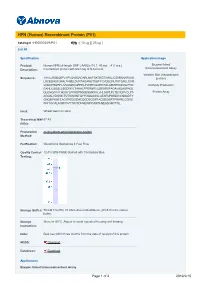
  • HPN (Human) Recombinant Protein (P01)
    HPN (Human) Recombinant Protein (P01) Catalog # : H00003249-P01 規格 : [ 10 ug ] [ 25 ug ] List All Specification Application Image Product Human HPN full-length ORF ( AAH25716.1, 40 a.a. - 417 a.a.) Enzyme-linked Immunoabsorbent Assay Description: recombinant protein with GST-tag at N-terminal. Western Blot (Recombinant Sequence: VAVLLRSDQEPLYPVQVSSADARLMVFDKTEGTWRLLCSSRSNARVAG protein) LSCEEMGFLRALTHSELDVRTAGANGTSGFFCVDEGRLPHTQRLLEVIS VCDCPRGRFLAAICQDCGRRKLPVDRIVGGRDTSLGRWPWQVSLRYD Antibody Production GAHLCGGSLLSGDWVLTAAHCFPERNRVLSRWRVFAGAVAQASPHGL QLGVQAVVYHGGYLPFRDPNSEENSNDIALVHLSSPLPLTEYIQPVCLPA Protein Array AGQALVDGKICTVTGWGNTQYYGQQAGVLQEARVPIISNDVCNGADFY GNQIKPKMFCAGYPEGGIDACQGDSGGPFACEDSISRTPRWRLCGIVS WGTGCALAQKPGVYTKVSDFREWIFQAIKTHSEASGMVTQL Host: Wheat Germ (in vitro) Theoretical MW 67.43 (kDa): Preparation in vitro wheat germ expression system Method: Purification: Glutathione Sepharose 4 Fast Flow Quality Control 12.5% SDS-PAGE Stained with Coomassie Blue. Testing: Storage Buffer: 50 mM Tris-HCI, 10 mM reduced Glutathione, pH=8.0 in the elution buffer. Storage Store at -80°C. Aliquot to avoid repeated freezing and thawing. Instruction: Note: Best use within three months from the date of receipt of this protein. MSDS: Download Datasheet: Download Applications Enzyme-linked Immunoabsorbent Assay Page 1 of 2 2019/2/15 Western Blot (Recombinant protein) Antibody Production Protein Array Gene Information Entrez GeneID: 3249 GeneBank BC025716 Accession#: Protein AAH25716.1 Accession#: Gene Name: HPN Gene Alias: TMPRSS1 Gene hepsin
    [Show full text]
  • Peripheral Nerve Single-Cell Analysis Identifies Mesenchymal Ligands That Promote Axonal Growth
    Research Article: New Research Development Peripheral Nerve Single-Cell Analysis Identifies Mesenchymal Ligands that Promote Axonal Growth Jeremy S. Toma,1 Konstantina Karamboulas,1,ª Matthew J. Carr,1,2,ª Adelaida Kolaj,1,3 Scott A. Yuzwa,1 Neemat Mahmud,1,3 Mekayla A. Storer,1 David R. Kaplan,1,2,4 and Freda D. Miller1,2,3,4 https://doi.org/10.1523/ENEURO.0066-20.2020 1Program in Neurosciences and Mental Health, Hospital for Sick Children, 555 University Avenue, Toronto, Ontario M5G 1X8, Canada, 2Institute of Medical Sciences University of Toronto, Toronto, Ontario M5G 1A8, Canada, 3Department of Physiology, University of Toronto, Toronto, Ontario M5G 1A8, Canada, and 4Department of Molecular Genetics, University of Toronto, Toronto, Ontario M5G 1A8, Canada Abstract Peripheral nerves provide a supportive growth environment for developing and regenerating axons and are es- sential for maintenance and repair of many non-neural tissues. This capacity has largely been ascribed to paracrine factors secreted by nerve-resident Schwann cells. Here, we used single-cell transcriptional profiling to identify ligands made by different injured rodent nerve cell types and have combined this with cell-surface mass spectrometry to computationally model potential paracrine interactions with peripheral neurons. These analyses show that peripheral nerves make many ligands predicted to act on peripheral and CNS neurons, in- cluding known and previously uncharacterized ligands. While Schwann cells are an important ligand source within injured nerves, more than half of the predicted ligands are made by nerve-resident mesenchymal cells, including the endoneurial cells most closely associated with peripheral axons. At least three of these mesen- chymal ligands, ANGPT1, CCL11, and VEGFC, promote growth when locally applied on sympathetic axons.
    [Show full text]
  • Association of 19Q, 8Q24 Regions and Mismatch Repair (MMR) Genes with Prostate Cancer in Caucasians
    Association of 19q, 8q24 regions and Mismatch Repair (MMR) Genes with Prostate Cancer in Caucasians A dissertation submitted to the Division of Research and Advanced Studies of the University of Cincinnati in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY in the Department of Environmental Health of the College of Medicine June, 2008 by Prodipto Pal M.B.B.S., University of Calcutta, Calcutta, India, 2000 Committee: Dr. Ranjan Deka, Ph.D. (Chair) Dr.Ranajit Chakraborty, Ph.D. Dr. Charles Ralph Buncher D.Sc. Dr. Daniel Woo, M.S., M.D. Dr. Divakar Choubey, Ph.D. ABSTRACT Prostate cancer (PCa) is the most commonly diagnosed visceral malignancy with over one-third of all incident cancers and the second leading cause of cancer deaths in men in the United States. Age, ethnicity and family history are among the classical epidemiological risk factors. Both environmental and genetic factors contribute to the etiopathogenesis of PCa. The region on 19q11-13, identified through linkage and association studies, was previously shown to harbor genes for PCa susceptibility as well as for biologic aggressiveness. Recently, admixture mapping and a number of independently performed genome-wide association studies (GWAS) further identified strong association signals on chromosome 8q24. The only biologically plausible candidate gene for cancers on 8q24 is the myc oncogene, located ~500 kb downstream to the identified region. The myc protein is a key regulator of cell cycle, growth and differentiation, apoptosis, genomic instability and angiogenesis. At the cellular level, myc synergistically interacts with mutL homolog 1 (MLH1), one of the key genes in mismatch repair (MMR) of DNA.
    [Show full text]
  • Primed to Die: an Investigation of the Genetic Mechanisms Underlying Noise-Induced
    bioRxiv preprint doi: https://doi.org/10.1101/2021.03.12.435183; this version posted March 12, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. 1 Title. 2 Primed to Die: An Investigation of the Genetic Mechanisms Underlying Noise-Induced 3 Hearing Loss and Cochlear Damage in Homozygous Foxo3-knockout Mice 4 5 Running title. 6 Noise induced outer hair cell loss in Foxo3 mutant mice 7 8 Authors. 9 Holly J. Beaulac1, Felicia Gilels1†, Jingyuan Zhang1††, Sarah Jeoung2, and Patricia M. White1* 10 11 Institutional Affiliations. 12 1Department of Neuroscience, Ernest J. Del Monte Institute for Neuroscience, University of 13 Rochester School of Medicine and Dentistry, Rochester, NY, USA. 14 15 2University of Rochester School of Medicine and Dentistry, Rochester, NY, USA. 16 17 †Now at Department of Pathology, University of Rochester School of Medicine and Dentistry, 18 Rochester, NY, USA. 19 20 ††Now at Department of Otolaryngology, Otolaryngology-Head and Neck Surgery, Harvard 21 Medical School, Boston Children’s Hospital Center for Life Science, Boston, MA, USA. 22 23 (*) Corresponding Author. Department of Neuroscience, Ernest J. Del Monte Institute for 24 Neuroscience, University of Rochester School of Medicine and Dentistry, 601 Elmwood Avenue, 25 Rochester, NY, 14642, USA. Email: [email protected]; Phone: 585-273-2340 26 1 bioRxiv preprint doi: https://doi.org/10.1101/2021.03.12.435183; this version posted March 12, 2021. The copyright holder for this preprint (which was not certified by peer review) is the author/funder.
    [Show full text]