DOCSLIB.ORG

Designing Digital Sequential Logic Circuits © N

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Designing Digital Sequential Logic Circuits © N Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Take-Home Exercise • Assume you want the counter below to count mod-6 backward. That is, it would count 0-5-4-3-2-1-0, etc. Assume it is reset on start- up, and design the wiring to make the counter count properly. • Major hint that was supplied: Remember the K-map method will work for ANY counter. Note: x is the most significant bit, z the least significant. z y x 1 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Designing Sequential Logic • Last lecture demonstrated the design of two simple counters (a third counter was a homework problem). • Today’s exercise: Three additional designs: – A modulo-10 binary counter – A timer or signal generator – A “sequential” multiplexer • Note that all the designs utilize counters. 5 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Design 1: A Decimal Counter • A “decimal counter” is one that counts modulo ten. • This is a realistic design, since in many electronic devices or appliances, it is often necessary to count in tens. • We will design only a single 0-9 counter, recognizing that we can count to 99 or 999 by simply adding more counter digits. • We will need a 4-bit counter (counting up to 9—1001—requires 4 bits). • The counter must: – Count from zero to nine and reset on the tenth clock pulse. – Count synchronously (as usual), that is, in parallel, not ripple. – Have the four counter bits available as outputs, so that they might be decoded to indicate various counts, from 0 to 9. 6 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science First Step: A Four-Bit (Modulo 16) Counter • In general, the best way to design any modulo-m counter (m not a power of 2) is to start with the smallest 2n counter that will count up to m. • In our case, we need a 4-bit counter (as mentioned on the previous page), as it takes 4 bits to count to 9. • Thus, we will start with a four-bit, modulo-16 counter. Once we have it, we can modify it to count modulo 10. • So as our first step, we will design that modulo-16 counter. It turns out that this design will also help us in the other two design exercises in this lecture. 7 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Modulo-16 Counter 1 LSB 2nd LSB 2nd MSB MSB Reset Clock • We are building a parallel or synchronous counter. Therefore, the clock is connected to all four stages of the counter as shown above. • We remember that for any 2n counter, the lowest stage is always connected to logic 1. Now we only have to consider the other three stages. • We will use the “truth table method” to find T for the last three stages of the counter. 8 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Truth-Table/K-Map Approach to Counter Design • Using this approach, we will make a truth table for the T inputs to each counter flip-flop versus the count. • We remember that for a T-FF, if the T input is 1, the counter stage will change states on the clock pulse. • However, if the T input is 0, when the input clock ticks, the flip-flop will not change states. • We normally make a composite truth table for all necessary stages (in this case, three), but then consider the counter stages, or flip-flops, one at a time to define the T for each count. Then we transfer this information to the Karnaugh map. 9 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Truth Table for Bit y T-Input Count T-Input y yNEXT • For a 4-bit counter, the truth tables wxyz will have 16 possibilities (i.e., the 16 0 0 0 0 0 0 0 counts of the counter). 0 0 0 1 1 0 1 • To eliminate calling the counter bits 0 0 1 0 0 1 1 “LSB, second LSB,” etc., we call the 0 0 1 1 1 1 0 counter outputs w, x, y, and z (where 0 1 0 0 0 0 0 w = MSB). 0 1 0 1 1 0 1 • Omitting z as noted, we examine the 0 1 1 0 0 1 1 Q output of y (shaded green), along 0 1 1 1 1 1 0 with its next output state (brackets). 1 0 0 0 0 0 0 These are then listed as “y” and 1 0 0 1 1 0 1 yNEXT” as before. 1 0 1 0 0 1 1 • As in the previous lecture, comparing 1 0 1 1 1 1 0 the y values tell us what the T-input 1 1 0 0 0 0 0 should be. If y = yNEXT, T = 0, but if 1 1 0 1 1 0 1 y ≠ yNEXT, T = 1. 1 1 1 0 0 1 1 1 1 1 1Etc. 1 1 0 10 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Karnaugh Map for Bit y T-Input • As usual, we plot the 1’s from the truth table on a Karnaugh map, just as we did for the modulo-8 and yz modulo-6 counters in the last lecture. 00 01 11 10 • From the K-Map, a simplifying prime 1 1 implicant is identified. 00 • Clearly, the implicant does not 01 1 1 depend on w, x, or y. wx 11 1 1 • Therefore we can define the Boolean expression or term for the T-input to 10 1 1 the counter bit y as: Ty = z • Note that this is just the T input we get using our “rule.” 11 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Bit y T Input Connected Tzy = 1 z y x w Reset Clock • Our timer counter circuit now looks as shown above, with the new w-x-y-z labels, and with the y-input connected. 12 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Truth Table for Bit x T-Input • The truth table is made up for Count T-Input x xNEXT w x y z bit x as we did for bit y, 0 0 0 0 0 0 0 comparing the value of x for 0 0 0 1 0 0 0 each count to the value of x in 0 0 1 0 0 0 0 0 0 1 1 1 0 1 the next count. 0 1 0 0 0 1 1 • These are then plotted in the 0 1 0 1 0 1 1 0 1 1 0 0 1 1 right two columns. 0 1 1 1 1 1 0 • As before, When x and x 1 0 0 0 0 0 0 NEXT 1 0 0 1 0 0 0 are equal, T is 0. When they 1 0 1 0 0 0 0 are different, T is 1. 1 0 1 1 1 0 1 1 1 0 0 0 1 1 • Note that there are fewer 1’s 1 1 0 1 0 1 1 on the table in the T-input 1 1 1 0 0 1 1 1 1 1 1 1 1 0 column because the 2nd MSB, Etc. x, will toggle fewer times. 13 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Karnaugh Map for Bit x T-Input • The bit x T-input K-map is shown. yz • As before, there is an obvious 00 01 11 10 simplifying Boolean expression for this T-input. 00 1 • We can see that outputs w and 01 1 wx x do not affect the switching of 11 1 2nd MSB. 10 1 • Given the Karnaugh map shown, what is the Boolean expression for Tx. Tx = yz 14 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Bit x T-Input Connected Tx = yz 1 z Tzy = y x w Reset Clock • Note that the inputs for x, y, and z are exactly the same result that we got for our three T inputs on our modulo-8 counter, just as we would expect. • We now follow our “longer procedure” to define the bit w T-input. 15 Lecture #9: Designing Digital Sequential Logic Circuits © N. B. Dodge 9/15 Erik Jonsson School of Engineering and The University of Texas at Dallas Computer Science Bit w T-Input Truth Table Count T-Input w wNEXT wxyz • We proceed in our analysis as 0 0 0 0 0 0 0 before.
Load more

Recommended publications
  • Binary Counter
    Systems I: Computer Organization and Architecture Lecture 8: Registers and Counters Registers • A register is a group of flip-flops. – Each flip-flop stores one bit of data; n flip-flops are required to store n bits of data. – There are several different types of registers available commercially. – The simplest design is a register consisting only of flip- flops, with no other gates in the circuit. • Loading the register – transfer of new data into the register. • The flip-flops share a common clock pulse (frequently using a buffer to reduce power requirements). • Output could be sampled at any time. • Clearing the flip-flop (placing zeroes in all its bit) can be done through a special terminal on the flip-flop. 1 4-bit Register I0 D Q A0 Clock C I1 D Q A1 C I D Q 2 A2 C D Q A I3 3 C Clear Registers With Parallel Load • The clock usually provides a steady stream of pulses which are applied to all flip-flops in the system. • A separate control system is needed to determine when to load a particular register. • The Register with Parallel Load has a separate load input. – When it is cleared, the register receives it output as input. – When it is set, it received the load input. 2 4-bit Register With Parallel Load Load D Q A0 I0 C D Q A1 C I1 D Q A2 I2 C D Q A3 I3 C Clock Shift Registers • A shift register is a register which can shift its data in one or both directions.
    [Show full text]
  • Cross Architectural Power Modelling
    Cross Architectural Power Modelling Kai Chen1, Peter Kilpatrick1, Dimitrios S. Nikolopoulos2, and Blesson Varghese1 1Queen’s University Belfast, UK; 2Virginia Tech, USA E-mail: [email protected]; [email protected]; [email protected]; [email protected] Abstract—Existing power modelling research focuses on the processor are extensively explored using a cumbersome trial model rather than the process for developing models. An auto- and error approach after which a suitable few are selected [7]. mated power modelling process that can be deployed on different Such an approach does not easily scale for various processor processors for developing power models with high accuracy is developed. For this, (i) an automated hardware performance architectures since a different set of hardware counters will be counter selection method that selects counters best correlated to required to model power for each processor. power on both ARM and Intel processors, (ii) a noise filter based Currently, there is little research that develops automated on clustering that can reduce the mean error in power models, and (iii) a two stage power model that surmounts challenges in methods for selecting hardware counters to capture proces- using existing power models across multiple architectures are sor power over multiple processor architectures. Automated proposed and developed. The key results are: (i) the automated methods are required for easily building power models for a hardware performance counter selection method achieves compa- collection of heterogeneous processors as seen in traditional rable selection to the manual method reported in the literature, data centers that host multiple generations of server proces- (ii) the noise filter reduces the mean error in power models by up to 55%, and (iii) the two stage power model can predict sors, or in emerging distributed computing environments like dynamic power with less than 8% error on both ARM and Intel fog/edge computing [8] and mobile cloud computing (in these processors, which is an improvement over classic models.
    [Show full text]
  • Experiment No
    1 LIST OF EXPERIMENTS 1. Study of logic gates. 2. Design and implementation of adders and subtractors using logic gates. 3. Design and implementation of code converters using logic gates. 4. Design and implementation of 4-bit binary adder/subtractor and BCD adder using IC 7483. 5. Design and implementation of 2-bit magnitude comparator using logic gates, 8- bit magnitude comparator using IC 7485. 6. Design and implementation of 16-bit odd/even parity checker/ generator using IC 74180. 7. Design and implementation of multiplexer and demultiplexer using logic gates and study of IC 74150 and IC 74154. 8. Design and implementation of encoder and decoder using logic gates and study of IC 7445 and IC 74147. 9. Construction and verification of 4-bit ripple counter and Mod-10/Mod-12 ripple counter. 10. Design and implementation of 3-bit synchronous up/down counter. 11. Implementation of SISO, SIPO, PISO and PIPO shift registers using flip-flops. KCTCET/2016-17/Odd/3rd/ETE/CSE/LM 2 EXPERIMENT NO. 01 STUDY OF LOGIC GATES AIM: To study about logic gates and verify their truth tables. APPARATUS REQUIRED: SL No. COMPONENT SPECIFICATION QTY 1. AND GATE IC 7408 1 2. OR GATE IC 7432 1 3. NOT GATE IC 7404 1 4. NAND GATE 2 I/P IC 7400 1 5. NOR GATE IC 7402 1 6. X-OR GATE IC 7486 1 7. NAND GATE 3 I/P IC 7410 1 8. IC TRAINER KIT - 1 9. PATCH CORD - 14 THEORY: Circuit that takes the logical decision and the process are called logic gates.
    [Show full text]
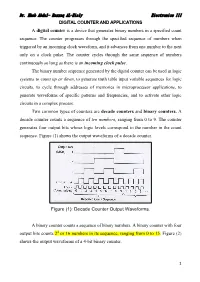
  • 1 DIGITAL COUNTER and APPLICATIONS a Digital Counter Is
    Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III DIGITAL COUNTER AND APPLICATIONS A digital counter is a device that generates binary numbers in a specified count sequence. The counter progresses through the specified sequence of numbers when triggered by an incoming clock waveform, and it advances from one number to the next only on a clock pulse. The counter cycles through the same sequence of numbers continuously so long as there is an incoming clock pulse. The binary number sequence generated by the digital counter can be used in logic systems to count up or down, to generate truth table input variable sequences for logic circuits, to cycle through addresses of memories in microprocessor applications, to generate waveforms of specific patterns and frequencies, and to activate other logic circuits in a complex process. Two common types of counters are decade counters and binary counters. A decade counter counts a sequence of ten numbers, ranging from 0 to 9. The counter generates four output bits whose logic levels correspond to the number in the count sequence. Figure (1) shows the output waveforms of a decade counter. Figure (1): Decade Counter Output Waveforms. A binary counter counts a sequence of binary numbers. A binary counter with four output bits counts 24 or 16 numbers in its sequence, ranging from 0 to 15. Figure (2) shows-the output waveforms of a 4-bit binary counter. 1 Dr. Ehab Abdul- Razzaq AL-Hialy Electronics III Figure (2): Binary Counter Output Waveforms. EXAMPLE (1): Decade Counter. Problem: Determine the 4-bit decade counter output that corresponds to the waveforms shown in Figure (1).
    [Show full text]
  • Design and Implementation of High Speed Counters Using “MUX Based Full Adder (MFA)”
    IOSR Journal of Electronics and Communication Engineering (IOSR-JECE) e-ISSN: 2278-2834,p- ISSN: 2278-8735.Volume 14, Issue 4, Ser. I (Jul.-Aug. 2019), PP 57-64 www.iosrjournals.org Design and Implementation of High speed counters using “MUX based Full Adder (MFA)” K.V.Jyothi1, G.P.S. Prashanti2, 1Student, 2Assistant Professor 1,2,(Department of Electronics and Communication Engineering, Gayatri Vidya Parishad College of Engineering For Women,Visakhapatnam, Andhra Pradesh, India) Corresponding Author: K.V.Jyothi Abstract: In this brief, a new binary counter design is proposed. Counters are used to determine how many number of inputs are active (in the logic ONE state) for multi input circuits. In the existing systems 6:3 and 7:3 Counters are designed with full and half adders, parallel counters, stacking circuits. It uses 3-bit stacking and 6-bit stacking circuits which group all the “1” bits together and then stacks are converted into binary counts. This leads to increase in delay and area. To overcome this problem “MUX based Full adder (MFA)” 6:3 and 7:3 counters are proposed. The backend counter simulations are achieved by using MENTOR GRAPHICS in 130nm technology and frontend simulations are done by using XILINX. This MFA counter is faster than existing stacking counters and also consumesless area. Additionally, using this counters in Wallace tree multiplier architectures reduces latency for 64 and 128-bit multipliers. Keywords: stacking circuits, parallel counters,High speed counters, MUX based full adder (MFA) counter,Mentor graphics,Xilinx,SPARTAN-6 FPGA. ----------------------------------------------------------------------------------------------------------------------------- ---------- Date of Submission: 28-07-2019 Date of acceptance: 13-08-2019 ----------------------------------------------------------------------------------------------------------------------------- ---------- I.
    [Show full text]
  • Hardware-Assisted Rootkits: Abusing Performance Counters on the ARM and X86 Architectures
    Hardware-Assisted Rootkits: Abusing Performance Counters on the ARM and x86 Architectures Matt Spisak Endgame, Inc. [email protected] Abstract the OS. With KPP in place, attackers are often forced to move malicious code to less privileged user-mode, to ele- In this paper, a novel hardware-assisted rootkit is intro- vate privileges enabling a hypervisor or TrustZone based duced, which leverages the performance monitoring unit rootkit, or to become more creative in their approach to (PMU) of a CPU. By configuring hardware performance achieving a kernel mode rootkit. counters to count specific architectural events, this re- Early advances in rootkit design focused on low-level search effort proves it is possible to transparently trap hooks to system calls and interrupts within the kernel. system calls and other interrupts driven entirely by the With the introduction of hardware virtualization exten- PMU. This offers an attacker the opportunity to redirect sions, hypervisor based rootkits became a popular area control flow to malicious code without requiring modifi- of study allowing malicious code to run underneath a cations to a kernel image. guest operating system [4, 5]. Another class of OS ag- The approach is demonstrated as a kernel-mode nostic rootkits also emerged that run in System Manage- rootkit on both the ARM and Intel x86-64 architectures ment Mode (SMM) on x86 [6] or within ARM Trust- that is capable of intercepting system calls while evad- Zone [7]. The latter two categories, which leverage vir- ing current kernel patch protection implementations such tualization extensions, SMM on x86, and security exten- as PatchGuard.
    [Show full text]
  • Central Processing Unit and Microprocessor Video
    Components Main articles: Central processing unit and Microprocessor Video demonstrating the standard components of a "slimline" computer A general purpose computer has four main components: the arithmetic logic unit (ALU), the control unit, the memory, and the input and output devices (collectively termed I/O). These parts are interconnected by buses, often made of groups of wires. Inside each of these parts are thousands to trillions of small electrical circuits which can be turned off or on by means of an electronic switch. Each circuit represents a bit (binary digit) of information so that when the circuit is on it represents a “1”, and when off it represents a “0” (in positive logic representation). The circuits are arranged in logic gates so that one or more of the circuits may control the state of one or more of the other circuits. The control unit, ALU, registers, and basic I/O (and often other hardware closely linked with these) are collectively known as a central processing unit (CPU). Early CPUs were composed of many separate components but since the mid-1970s CPUs have typically been constructed on a single integrated circuit called a microprocessor. Control unit Main articles: CPU design and Control unit Diagram showing how a particularMIPS architecture instruction would be decoded by the control system The control unit (often called a control system or central controller) manages the computer's various components; it reads and interprets (decodes) the program instructions, transforming them into a series of control signals which activate other parts of the computer.[50]Control systems in advanced computers may change the order of some instructions so as to improve performance.
    [Show full text]
  • The Central Processing Unit (CPU)
    The Central Processing Unit (CPU) Crash Course Computer Science #7 The Central Processing Unit https://www.youtube.com/watch?v=FZGugFqdr60 Internals ● Arithmetic Logic Unit (ALU) ● Control Unit (CU) ● Registers ● Cache Memory ● The Fetch-Execute Cycle Arithmetic Logic Unit An arithmetic logic unit (ALU) is a digital circuit used to perform arithmetic and logic ​ operations. It represents the fundamental building block of the central processing unit ​ (CPU) of a computer. Modern CPUs contain very powerful and complex ALUs. In addition to ALUs, modern CPUs contain a control unit (CU). Most of the operations of a CPU are performed by one or more ALUs, which load data from ​ input registers. A register is a small amount of storage available as part of a CPU. The ​ control unit tells the ALU what operation to perform on that data and the ALU stores the result in an output register. The control unit moves the data between these registers, the ALU, and memory. Control Unit A control unit coordinates how data moves around a cpu. The control unit (CU) is a ​ ​ component of a computer's central processing unit (CPU) that directs operation of the processor. It tells the computer's memory, arithmetic/logic unit and input and output devices how to respond to a program's instructions. ● The control unit obtains data / instructions from memory ● Interprets / decodes the instructions into commands / signals ● Controls transfer of instructions and data in the CPU ● Coordinates the parts of the CPU Registers In computer architecture, a processor register is a quickly accessible location available ​ to a digital processor's central processing unit (CPU).
    [Show full text]
  • Processor Hardware Counter Statistics As a First-Class System Resource
    ∗ Processor Hardware Counter Statistics As A First-Class System Resource XiaoZhang SandhyaDwarkadas GirtsFolkmanis KaiShen Department of Computer Science, University of Rochester Abstract which hides the differences and details of each hardware platform from the user. Today's processors provide a rich source of statis- In this paper, we argue that processor hardware coun- tical information on program execution characteristics ters are a first-class resource, warranting general OS uti- through hardware counters. However, traditionally, op- lization and requiring direct OS management. Our dis- erating system (OS) support for and utilization of the cussion is within the context of the increasing ubiquity hardware counter statistics has been limited and ad hoc. and variety of hardware resource-sharing multiproces- In this paper, we make the case for direct OS manage- sors. Examples are memory bus-sharing symmetric mul- ment of hardware counter statistics. First, we show the tiprocessors (SMPs), L2 cache-sharing chip multiproces- utility of processor counter statistics in CPU scheduling sors (CMPs), and simultaneous multithreading (SMTs), (for improved performance and fairness) and in online where many hardware resources including even the pro- workload modeling, both of which require online contin- cessor counter registers are shared. uous statistics (as opposed to ad hoc infrequent uses). Processor metrics can identify hardware resource con- Second, we show that simultaneous system and user use tention on resource-sharing multiprocessors in addition of hardware counters is possible via time-division multi- to providing useful information on application execution plexing. Finally, we highlight potential counter misuses behavior. We reinforce existing results to demonstrate to indicate that the OS should address potential security multiple uses of counter statistics in an online continu- issues in utilizing processor counter statistics.
    [Show full text]
  • Tutorial on Adder and Subtractor Logic Circuits Digital Adder: 1. Half Adder 2. Full Adder. Half Adder- Full Adder
    Tutorial on Adder and Subtractor Logic Circuits Digital Adder: In digital electronics an adder is a logic circuit that implements addition of numbers. In many computers and other types of processors, adders are used to calculate addresses, similar operations and table indices in the arithmetic logic unit (ALU) and also in other parts of the processors. These can be built for many numerical representations like binary coded decimal or excess-3. Adders are classified into two types: 1. Half adder 2. Full adder. Half Adder- The half adder circuit is required to add two input digits (for Ex. A and B) and generate a carry and sum. The half adder adds two binary digits called as augend and addend and produces two outputs as sum and carry (XOR is applied to both inputs to produce sum and AND gate is applied to both inputs to produce carry). It means half adder circuits can add only two digits in other words if we need to add more than 2 digits it will not work, so, it the limitation of an half adder electronic circuits. To resolve this problem a full adder circuit is required. Application- The ALU of a computer uses half adder to compute the binary addition operation on two bits. Half adder is used to make full adder as a full adder requires 3 inputs, the third input being an input carry i.e. we will be able to cascade the carry bit from one adder to the other. Ripple carry adder is possible to create a logical circuit using multiple full adders to add N- bit numbers.
    [Show full text]
  • Arithmetic Logic Unit Architectures with Dynamically Defined Precision
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 12-2015 ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION Getao Liang University of Tennessee - Knoxville, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Part of the Computer and Systems Architecture Commons, Digital Circuits Commons, and the VLSI and Circuits, Embedded and Hardware Systems Commons Recommended Citation Liang, Getao, "ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION. " PhD diss., University of Tennessee, 2015. https://trace.tennessee.edu/utk_graddiss/3592 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Getao Liang entitled "ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Computer Engineering. Gregory D. Peterson, Major Professor We have read this dissertation and recommend its acceptance: Jeremy Holleman, Qing Cao, Joshua Fu Accepted for the Council: Carolyn R. Hodges Vice Provost and Dean of the Graduate School (Original signatures are on file with official studentecor r ds.) ARITHMETIC LOGIC UNIT ARCHITECTURES WITH DYNAMICALLY DEFINED PRECISION A Dissertation Presented for the Doctor of Philosophy Degree The University of Tennessee, Knoxville Getao Liang December 2015 DEDICATION This dissertation is dedicated to my wife, Jiemei, and my family.
    [Show full text]
  • Solved Problems from Chapters 3, 5, 6, 7, 8
    Chapter 3 Examples of Solved Problems for Chapter3,5,6,7,and8 This document presents some typical problems that the student may encounter, and shows how such problems can be solved. Note that the numbering of examples below is taken from the 2nd edition of the book Fundamentals of Digital Logic with VHDL Design. Since not all of these examples are relevant to ECE241, the numbering of examples, and some figure numbers, are not always sequential in this document. Example 3.9 Problem: We introduced standard cell technology in section 3.7. In this technology, circuits are built by interconnecting building-block cells that implement simple functions, like basic logic gates. A commonly used type of standard cell are the and-or-invert (AOI) cells, which can be efficiently built as CMOS complex gates. Consider the AOI cell shown in Figure 3.70. This cell implements the function f = x1x2 + x3x4 + x5. Derive the CMOS complex gate that implements this cell. Figure 3.70. The AOI cell for Example 3.9. Solution: Applying Demorgan’s theorem in two steps gives f = x1x2 · x3x4 · x5 =(x1 + x2) · (x3 + x4) · x5 1 Since all input variables are complemented in this expression, we can directly derive the pull-up network as having parallel-connected PMOS transistors controlled by x1 and x2, in series with parallel-connected transistors controlled by x3 and x4, in series with a transistor controlled by x5. This circuit, along with the corresponding pull-down network, is shown in Figure 3.71. Figure 3.71. Circuit for Example 3.9.
    [Show full text]