DOCSLIB.ORG

EXPLICIT PARAMETERIZATION of EULER's ELASTICA 1. Introduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
EXPLICIT PARAMETERIZATION of EULER's ELASTICA 1. Introduction Ninth International Conference on Geometry, Geometry, Integrability and Quantization Integrability June 8–13, 2007, Varna, Bulgaria and Ivaïlo M. Mladenov, Editor IX SOFTEX, Sofia 2008, pp 175–186 Quantization EXPLICIT PARAMETERIZATION OF EULER’S ELASTICA PETER A. DJONDJOROV, MARIANA TS. HADZHILAZOVAy, IVAÏLO M. MLADENOVy and VASSIL M. VASSILEV Institute of Mechanics, Bulgarian Academy of Sciences Acad. G. Bonchev Str., Bl. 4, 1113 Sofia, Bulgaria yInstitute of Biophysics, Bulgarian Academy of Sciences Acad. G. Bonchev Str., Bl. 21, 1113 Sofia, Bulgaria Abstract. The consideration of some non-standard parametric Lagrangian leads to a fictitious dynamical system which turns out to be equivalent to the Euler problem for finding out all possible shapes of the lamina. Integrating the respective differential equations one arrives at novel explicit parameteri- zations of the Euler’s elastica curves. The geometry of the inflexional elastica and especially that of the figure “eight” shape is studied in some detail and the close relationship between the elastica problem and mathematical pendulum is outlined. 1. Introduction The elastic behaviour of roads and beams which attracts a continuous attention since the time of Galileo, Bernoulli and Euler has generated recently a renewed interest in plane [2, 3, 15], space [18] and space forms [1, 11]. The first elastic problem was posed by Galileo around 1638 who asked the question about the force required to break a beam set into a wall. James (or Jakob) Bernoulli raised in 1687 the question concerning the shape of the beam and had also succeeded in solving the case of the so called rectangular elastica (second case from the top in Fig. 1). Later on in 1742 Daniel Bernoulli wrote a letter to Euler in which he had suggested to him to solve the general problem of the elastica. Following closely this sugges- tion Euler cast the problem in the variational form and presented the solution in an Appendix to his book on variational calculus which appeared in 1744. Euler begins his investigation with establishing the equation of static equilibrium of the “lamina” by means of the variational techniques developed in his treatise and then rederives it from mechanical principles developed earlier by James Bernoulli. The 175 176 Peter Djondjorov, Mariana Hadzhilazova, Ivaïlo Mladenov and Vassil Vassilev Bernoulli-Euler theory which considers only bending deformations and neglects shear deformations and stretching of the center line of the beam is given in detail by Love [13]. The corresponding solutions were found by using the equivalence of the elastica with that of the mathematical pendulum (see also Section five below). Nine different classes can be distinguished and Love presents figures for the sev- enth of them (cf. Fig.1 below). Later on Birkhoff and de Boor [2] have found the fundamental equation of the Euler elastica without length constraint (i.e., the so called free elastica) 1 κ¨(s) + κ3(s) = 0: (1) 2 Here κ(s) is the curvature of the arclength parameterized smooth curve in the plane and the dots denote the derivatives with respect to its natural parameter s. In what follows we will derive the intrinsic equation of the non-free elastica by introducing a fictitious dynamical system and present its explicit solutions in terms of Jacobian elliptic functions and elliptic integrals. We hope that these dynamical considerations could be of some interest in the many other situations as well. 2. The Fictitious Dynamical System Assuming that λ is a positive real number let us consider the following system of nonlinearly coupled ordinary differential equations x¨ − λzz_ = 0 (2) z¨ + λzx_ = 0: (3) It is quite natural to consider equations (2) and (3) as equations describing the dynamics of a particle moving in XOZ plane. It is easy to check by a direct computation that equations (2) and (3) are the Euler- Lagrange equations d d F − F = 0; F − F = 0 (4) ds x_ x ds z_ z associated with an action functional whose Lagrangian F can be taken of the form 1 λ F (x; z; x;_ z;_ t) = x_ 2 +z _2 − z (zx_ − xz_) 2 3 in which λ plays the role of the Lagrange multiplier. The particle trajectories γ(s) = x (s) determined by the parametric equation x (s) = (x(s); z (s)) (5) which we will assume to be traced with unit speed, i.e., x_ 2(s) +z _2(s) = 1 (6) Explicit Parameterization of Euler’s Elastica 177 describe the plane curve we are seeking. 3. Integration A theorem in the classical differential geometry (see e.g. [17]) claims that any plane curves is determined uniquely (up to Euclidean motion in the plane) by its curvature which in our settings can be written as κ(s) =x _z¨ − z_x:¨ (7) It is easy to see also that the equations (2) and (3) imply κ(s) = −λz(s): (8) This claim can be proved in the following manner: multiplying (3) by x_ and sub- tracting from it the result of multiplication of (2) by z_ and taking into account (6) we get exactly (8) x_z¨ − z_x¨ = −λz: Actually, the integration of (2) is immediate and produces λz2 x_ = + µ (9) 2 where µ is the integration constant. Inserting the expression for x_ from (9) into (3) leads to the equation λ2z3 z¨ + + λµz = 0: (10) 2 When rewritten in terms of the curvature the above equation becomes 1 κ¨(s) + κ3(s) + σκ(s) = 0; σ = λµ (11) 2 which is known as the intrinsic equation [3] of the elastica with tension σ and in this way we have reduced our fictitious dynamical system to the elastica problem. Continuing with the integration of (10) we get λ2z4 z_2 = − − λµz2 + C (12) 4 where C is another integration constant which however is not arbitrary but fixed by (6), i.e., C = 1 − µ2: (13) It is a trivial matter to find that the right hand side of equation (12) can be factorized in the form λ2 2(1 − µ) 2(1 + µ) − z2 z2 + (14) 4 λ λ 178 Peter Djondjorov, Mariana Hadzhilazova, Ivaïlo Mladenov and Vassil Vassilev which allows the equation itself to be rewritten as Z dz λs r = · (15) 2(1−µ) 2 2 2(1+µ) 2 λ − z z + λ Examination of the above integral leads to the conclusion that µ should be strictly smaller than one and further analysis shows that we have the following obvious possibilities: A) µ 2 (−1; 1) B) µ = −1 C) µ < −1. These possibilities will be considered below case by case: a) Introducing 2(1 − µ) 2(1 + µ) a2 = ; c2 = · (16) λ λ The integration in this case can be done with the help of the Jacobian elliptic func- tion cn(u; k) in which u is the argument and k is the so called modulus of the elliptic function (for more details on the elliptic functions, their integrals and prop- erties see e.g. [7] and [10]) p p r1 − µ z(s) = a cn(− λs, k) = a cn( λs, k); k = (17) 2 b) The integration of the second case is performed via the hyperbolic functions and one easily gets p 2 sech(s λ) z(s) = p · (18) λ c) After some preparation the integration in the last case leads also to an expression in terms of Jacobian elliptic function. For that purpose we have to change the parameter µ with ν = −µ, which means that the range of the new parameter is the ν > 1 part of the real line. Besides, it turns out convenient to introduce new parameters a^ and c^ in place of a and c used in (15), i.e., 2(ν + 1) 2(ν − 1) a^2 = ; c^2 = (19) λ λ so that this time we have to evaluate Z dz λs = · (20) p(^a2 − z2)(z2 − c^2) 2 Integrating it we obtain s s s λ(ν + 1) λ(ν + 1) 2 z(s) =a ^ dn(− s; k^) =a ^ dn( s; k^); k^ = · (21) 2 2 ν + 1 Explicit Parameterization of Euler’s Elastica 179 The above results should be completed by the integration of equation (9) in the appropriate setting and in this way we find respectively the parameterizations: 2 p p A) x(s) = p E am λs, k ; k − s; z(s) = a cn( λs, k) λ p p 2 tanh( λs) 2 sech( λs) B) x(s) = p − s; z(s) = p (22) λ λ s s λ(ν + 1) λ(ν + 1) C) x(s) =aE ^ (am( s; k^); k^) − νs; z(s) =a ^ dn ( s; k^) 2 2 in which E(u; k) and F (u; k) (which will appear later on) denote the incomplete elliptic integrals of the second respectively first kind depending on the argument u and modulus k, and am (t; k) denotes the Jacobian amplitude function (cf. [7, 10]). Actually, the integral (20) can be expressed in a slightly different form and this gives another curve p 2 2 cn(u(s); k^) sn(u(s); k^) C0) x(s) =aE ^ (am(u(s); k^); k^) − − νs pλ(ν + 1) dn(u(s); k^) (23) s c^ λ(ν + 1) z(s) = ; u(s) = s dn(u(s); k^) 2 which coincides with (22 C) (as it should be) if translated along the X axis at distance ! p rν + 1 νK(k^) ± 2 E(am(K(k^); k^); k^) − λ pλ(ν + 1) where K(k^) is the complete elliptic integral of the first kind [7, 10]. 4. Some Geometrical Remarks A few comments are in order here. E.g., already Euler had detected nine species of elastic curves while in Fig.
Load more

Recommended publications
  • 'I Spy': Mike Leigh in the Age of Britpop (A Critical Memoir)
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Glasgow School of Art: RADAR 'I Spy': Mike Leigh in the Age of Britpop (A Critical Memoir) David Sweeney During the Britpop era of the 1990s, the name of Mike Leigh was invoked regularly both by musicians and the journalists who wrote about them. To compare a band or a record to Mike Leigh was to use a form of cultural shorthand that established a shared aesthetic between musician and filmmaker. Often this aesthetic similarity went undiscussed beyond a vague acknowledgement that both parties were interested in 'real life' rather than the escapist fantasies usually associated with popular entertainment. This focus on 'real life' involved exposing the ugly truth of British existence concealed behind drawing room curtains and beneath prim good manners, its 'secrets and lies' as Leigh would later title one of his films. I know this because I was there. Here's how I remember it all: Jarvis Cocker and Abigail's Party To achieve this exposure, both Leigh and the Britpop bands he influenced used a form of 'real world' observation that some critics found intrusive to the extent of voyeurism, particularly when their gaze was directed, as it so often was, at the working class. Jarvis Cocker, lead singer and lyricist of the band Pulp -exemplars, along with Suede and Blur, of Leigh-esque Britpop - described the band's biggest hit, and one of the definitive Britpop songs, 'Common People', as dealing with "a certain voyeurism on the part of the middle classes, a certain romanticism of working class culture and a desire to slum it a bit".
    [Show full text]
  • Student Lounge Revamped
    The Pride http://www.csusm.edu/pride California State University, San Marcos Vol VIII No. 5/ Tuesday, September 26,2000 Faculty Files Grievance By: Jayne Braman istration and faculty. University's Convocation, Pride Staff The "faculty workload issue" President Gonzalez stated, "We revolves around a grievance filed are a CSU campus and we do have Students have many factors by the San Marcos chapter of to follow system-wide guidelines to consider when deciding on the faculty union, the California and operate within our funding which college to attend. Many Faculty Association (CFA), which formula which is predicated on CSUSM students credit the small is pending arbitration scheduled 15 units per Full Time Equivalent classes, the writing requirement, for October 28. Although the Student (FTES) and 12 Direct and the availability of professors details of the arbitration are not Weighted Teaching Units (WTU) as factors that ultimately add made public, the outcome of this for faculty." value to their education as well hearing will set a precedent that "The faculty argues that fund- as to their degrees. Students have will determine the future direc- ing increases depend strictly on also noted that the reputation tion of faculty workload. FTES, not on faculty teaching 12, of the institution will continue CSUSM President Alexander units," according to Dr. George to influence the value of their Gonzalez explains, "Faculty is Diehr, local union CFA President degrees long after they leave this contracted to work twelve (12) and Professor of Management campus. credit hours per semester." Science. "In fact," Diehr con- The window of opportunity Gonzalez continues, "This labor tends, "there is no mention any- is still wide open for CSUSM contract is part of a collective- where of faculty being required to to decide its future direction.
    [Show full text]
  • BANANAZ Panorama BANANAZ Dokumente BANANAZ Regie: Ceri Levy
    PD_4974:PD_ 26.01.2008 17:53 Uhr Seite 222 Berlinale 2008 BANANAZ Panorama BANANAZ Dokumente BANANAZ Regie: Ceri Levy Großbritannien 2008 Dokumentarfilm mit Gorillaz Länge 92 Min. Damon Albarn Format 35 mm Jamie Hewlett Farbe Ibrahim Ferrer Dennis Hopper Stabliste De La Soul Buch, Kamera Ceri Levy D-12 Schnitt Seb Monk Shaun Ryder Mischung Robert Farr Bootie Brown Musik Gorillaz Produzenten Rachel Connors Ceri Levy Produktion Head Film Ltd. 87d Elsham Road GB-London W14 8HH [email protected] Weltvertrieb Hanway Films 24 Hanway Street GB-London W1T 1UH Tel.: +44 207 2900750 Fax: +44 207 2900751 [email protected] BANANAZ Die Gorillaz sind die Band der Stunde! Während sich viele Rock- und Pop - veteranen angesichts dramatischer Rückgänge ihrer Platten- und CD-Ver - käufe neue Absatzmärkte in den visuell orientierten Vertriebskanälen Kino, Fernsehen und DVD erst noch erschließen müssen, waren die Gorillaz von vorn herein als ein visuelles Ereignis konzipiert. Als die Band 1998 von Damon Albarn, dem Sänger der britischen Gruppe Blur, und dem Comic- Zeichner Jamie Hewlett („Tank Girl“) spontan während einer nächtlichen Unterhaltung in ihrer Londoner WG gegründet wurde, bestand sie zu - nächst nur aus vier fiktiven Comic-Gestalten: D, Murdoc, Noodle und Russel. Zwar wurden sie im Laufe der Zeit mit individuellen Biografien versehen, doch verbergen sich hinter ihnen stets wechselnde Musiker. Nach mehreren Singles, zwei Alben und zahlreichen Videoclips gibt der Film von Ceri Levy nun den Blick auf die realen Personen hinter den animierten Figuren frei. Sieben Jahre lang hat sich der Regisseur, der mit Damon Albarn seit langem befreundet ist, in dem Paralleluniversum, das sich um die Gorillaz inzwischen aufgebaut hat, für seinen Film frei bewegen können.
    [Show full text]
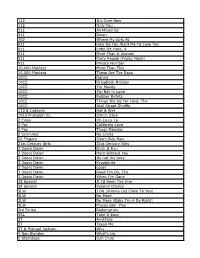
  • 112 It's Over Now 112 Only You 311 All Mixed up 311 Down
    112 It's Over Now 112 Only You 311 All Mixed Up 311 Down 702 Where My Girls At 911 How Do You Want Me To Love You 911 Little Bit More, A 911 More Than A Woman 911 Party People (Friday Night) 911 Private Number 10,000 Maniacs More Than This 10,000 Maniacs These Are The Days 10CC Donna 10CC Dreadlock Holiday 10CC I'm Mandy 10CC I'm Not In Love 10CC Rubber Bullets 10CC Things We Do For Love, The 10CC Wall Street Shuffle 112 & Ludacris Hot & Wet 1910 Fruitgum Co. Simon Says 2 Evisa Oh La La La 2 Pac California Love 2 Pac Thugz Mansion 2 Unlimited No Limits 20 Fingers Short Dick Man 21st Century Girls 21st Century Girls 3 Doors Down Duck & Run 3 Doors Down Here Without You 3 Doors Down Its not my time 3 Doors Down Kryptonite 3 Doors Down Loser 3 Doors Down Road I'm On, The 3 Doors Down When I'm Gone 38 Special If I'd Been The One 38 Special Second Chance 3LW I Do (Wanna Get Close To You) 3LW No More 3LW No More (Baby I'm A Do Right) 3LW Playas Gon' Play 3rd Strike Redemption 3SL Take It Easy 3T Anything 3T Tease Me 3T & Michael Jackson Why 4 Non Blondes What's Up 5 Stairsteps Ooh Child 50 Cent Disco Inferno 50 Cent If I Can't 50 Cent In Da Club 50 Cent In Da Club 50 Cent P.I.M.P. (Radio Version) 50 Cent Wanksta 50 Cent & Eminem Patiently Waiting 50 Cent & Nate Dogg 21 Questions 5th Dimension Aquarius_Let the sunshine inB 5th Dimension One less Bell to answer 5th Dimension Stoned Soul Picnic 5th Dimension Up Up & Away 5th Dimension Wedding Blue Bells 5th Dimension, The Last Night I Didn't Get To Sleep At All 69 Boys Tootsie Roll 8 Stops 7 Question
    [Show full text]
  • Arxiv:Math/9808099V3
    On the Moduli of a Quantized Elastica in P and KdV Flows: Study of Hyperelliptic Curves as an Extension of Euler’s Perspective of Elastica I Shigeki MATSUTANI∗ and Yoshihiro ONISHIˆ † ∗8-21-1 Higashi-Linkan Sagamihara, 228-0811 Japan †Faculty of Humanities and Social Sciences, Iwate University, Ueda, Morioka, Iwate, 020-8550 Japan Abstract Quantization needs evaluation of all of states of a quantized object rather than its stationary states P with respect to its energy. In this paper, we have investigated moduli elas of a quantized elastica, a quantized loop with an energy functional associated with the Schwarz derivative,M on a Riemann sphere P. Then it is proved that its moduli space is decomposed to a set of equivalent classes determined by flows obeying the Korteweg-de Vries (KdV) hierarchy which conserve the energy. Since the flow P obeying the KdV hierarchy has a natural topology, it induces topology in the moduli space elas. P M Using the topology, is classified. Melas Studies on a loop space in the category of topological spaces Top are well-established and its cohomological properties are well-known. As the moduli space of a quantized elastica can be regarded as a loop space in the category of differential geometry DGeom, we also proved an existence of a functor between a triangle category related to a loop space in Top and that in DGeom using the induced topology. As Euler investigated the elliptic integrals and its moduli by observing a shape of classical elastica on C, this paper devotes relations between hyperelliptic curves and a quantized elastica on P as an extension of Euler’s perspective of elastica.
    [Show full text]
  • Indie Mixtape Subscribers Can Get 10% Off This Can't-Miss Set by Entering the Code JONI10 Checkout
    :: View email as a web page :: The spring of 1995 was a crowded season in indie-rock history. Pavement dropped their polarizing third album, the willfully messy and frequently brilliant Wowee Zowee. Yo La Tengo continued their hit streak of low-key masterworks with Eletr-O-Pura. Illinois fuzz-rock quartet Hum hit hard with Youʼd Prefer An Astronaut, and Teenage Fanclub produced one of their finest jangle-pop efforts, Grand Prix. Wilco, Elastica, and Apples In Stereo put out well-regarded debuts. And Red House Painters hit a new high-water mark with Ocean Beach. But even in an era when classic indie records seemed to come out every week, there was nothing quite like Alien Lanes, the eighth full-length LP by a band from Dayton, Ohio called Guided By Voices. Released on April 4, 1995, Alien Lanes arrived with baked-in mythology. It had been supposedly recorded for just $10 in various concrete basements around Dayton by a group of blue-collar guys in their mid-30s. Uproxx dug into the history of this classic and produced this great oral history. -- Steven Hyden, Uproxx Cultural Critic and author of This Isn't Happening: Radiohead's "Kid A" And The Beginning Of The 21st Century OPENING TRACKS RINA SAWAYAMA This budding indie-pop star is among the buzziest acts to emerge this year, with an ear-catching single called “STFU” that’s like Carly Rae Jepsen if she spent years obsessing over Korn’s Follow The Leader. That pan-genre approach ultimately informs Sawayama — who was born in Japan and raised in London — and her aesthetic.
    [Show full text]
  • Crossword Puzzle
    ENTERTAINMENTpage 25 Technique • Friday, September 1, 2000 • 25 Crossword Puzzle! Just play it loud, ok? ENTERTAINMENT Bored in class? Itching to exercise your This week we’ve got six (count ‘em, mind-boggling vocabulary? Our new six!) CD reviews for your inspection. feature is right up your alley. Page 26 Look, listen, and love them all. Technique • Friday, Septemeber 1, 2000 ‘Art of War’ delivers nothing but paint-by-numbers action By Alan Back is sent in to change their minds becomes Public Enemy Number Has trouble drawing stick people any way he sees fit. Spying? No One. He finds himself cut off problem.Wiretapping? Fair from the rest of his team, with MPAA Rating: R game. Blackmail? He can swing authorities from both sides of Starring: Wesley Snipes, Anne that, too. the Pacific after him, as he races Archer, Maury Chaykin, to find the truth before the Marie Matiko situation explodes into an all- Director: Christian Duguay out war. Studio: Morgan Creek Films “How do you give Now, where to begin? Running Time: 117 minutes a medal to Mistake #1: cannibalizing a Rating: yy string of movies to assemble the somebody who plot. “The Fugitive,” “U.S. Mar- War is hell. The Art of War doesn’t exist for shals” and “Mission: Impossi- just feels like it. ble” are shoved through the meat If you’re pressed for time, stop something that grinder, with bits of “Lethal reading now and stay away from didn’t happen?” Weapon” (“I’m too f—in’ old any theater showing this film, for this,” says Maury Chaykin, which manages to commit just UN Secretary-General playing an irritating FBI agent) about every action-movie atroc- Douglas Thomas (Donald and “White Men Can’t Jump” ity known to man.
    [Show full text]
  • Masterwork, Benefit Concert, and Miscellaneous Choral Works By
    Three Dissertation Recitals: Masterwork, Benefit Concert, and Miscellaneous Choral Works by Adrianna L. Tam A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Musical Arts (Music: Conducting) in the University of Michigan 2019 Doctoral Committee: Associate Professor Eugene Rogers, Chair Professor Emeritus Jerry Blackstone Associate Professor Gabriela Cruz Associate Professor Julie Skadsem Associate Professor Gregory Wakefield Adrianna L. Tam [email protected] ORCID iD: 0000-0002-1732-5974 © Adrianna L. Tam 2019 TABLE OF CONTENTS ABSTRACT iii RECITAL 1: DURUFLÉ REQUIEM 1 Recital 1 Program 1 Recital 1 Program Notes and Texts 2 RECITAL 2: FLIGHT: MERCY, JOURNEY & LANDING 6 Recital 2 Program 6 Recital 2 Program Notes and Texts 8 RECITAL 3: VIDEO COMPILATION 21 Recital 3 Program 21 Recital 3 Program Notes and Texts 23 ii ABSTRACT Three dissertation recitals were presented in partial fulfillment of the requirements for the degree of Doctor of Musical Arts (Music: Conducting). The recitals included a broad range of repertoire, from the Baroque to modernity. The first recital was a performance of Duruflé’s Requiem, scored for chorus and organ, sung by a recital choir and soloists at Bethlehem United Church of Christ on Sunday, April 29, 2018. Scott VanOrnum played the organ, and University of Michigan (U-M) School of Music, Theatre & Dance doctoral students, Elise Eden and Leo Singer, joined as solo soprano and cellist, respectively. The second recital was a benefit concert held on January 27, 2019 at Ste. Anne de Detroit Catholic Church on behalf of the Prison Creative Arts Project. Guest singers and instrumentalists joined the core ensemble, Out of the Blue, to explore themes of mercy, journey, and landing.
    [Show full text]
  • Gigs of My Steaming-Hot Member of Loving His Music, Mention in Your Letter
    CATFISH & THE BOTTLEMEN Van McCann: “i’ve written 14 MARCH14 2015 20 new songs” “i’m just about BJORK BACK FROM clinging on to THE BRINK the wreckage” ENTER SHIKARI “ukiP are tAKING Pete US BACKWARDs” LAURA Doherty MARLING THE VERDICT ON HER NEW ALBUM OUT OF REHAB, INTO THE FUTURE ►THE ONLY INTERVIEW CLIVE BARKER CLIVE + Palma Violets Jungle Florence + The Machine Joe Strummer The Jesus And Mary Chain “It takes a man with real heart make to beauty out of the stuff that makes us weep” BLACK YELLOW MAGENTA CYAN 93NME15011142.pgs 09.03.2015 11:27 EmagineTablet Page HAMILTON POOL Home to spring-fed pools and lush green spaces, the Live Music Capital of the World® can give your next performance a truly spectacular setting. Book now at ba.com or through the British Airways app. The British Airways app is free to download for iPhone, Android and Windows phones. Live. Music. AustinTexas.org BLACK YELLOW MAGENTA CYAN 93NME15010146.pgs 27.02.2015 14:37 BAND LIST NEW MUSICAL EXPRESS | 14 MARCH 2015 Action Bronson 6 Kid Kapichi 25 Alabama Shakes 13 Laura Marling 42 The Amorphous Left & Right 23 REGULARS Androgynous 43 The Libertines 12 FEATURES Antony And The Lieutenant 44 Johnsons 12 Lightning Bolt 44 4 SOUNDING OFF Arcade Fire 13 Loaded 24 Bad Guys 23 Lonelady 45 6 ON REPEAT 26 Peter Doherty Bully 23 M83 6 Barli 23 The Maccabees 52 19 ANATOMY From his Thai rehab centre, Bilo talks Baxter Dury 15 Maid Of Ace 24 to Libs biographer Anthony Thornton Beach Baby 23 Major Lazer 6 OF AN ALBUM about Amy Winehouse, sobriety and Björk 36 Modest Mouse 45 Elastica
    [Show full text]
  • Leaf-Inhabiting Fungal Endophytes of F. Benjamina, F. Elastica, F. Religiosa
    Leaf-inhabiting fungal endophytes of F. benjamina, F. elastica, F. religiosa from Philippine tropical forests and German botanical greenhouses - Assessment of diversity, community composition and bioprospecting perspective I n a u g u r a l d i s s e r t a t i o n zur Erlangung des akademischen Grades Doktors der Naturwissenschaften (Dr. rer. nat.) an der Mathematisch-Naturwissenschaftlichen Fakultät Mathematisch-Naturwissenschaftlichen Fakultät der Ernst-Moritz-Arndt-Universität Greifswald vorgelegt von Michael Jay L. Solis geboren am 30.09.1976 in Bacolod City, Philippines Dekan: Prof. Dr. Werner Weitschies Gutachter:.........................................................PD. Dr. Martin Unterseher Gutachter:.........................................................Prof. Dr. Marc Stadler Tag der Promotion:................................08.04.2016 ......... PREFACE This cumulative dissertation is the culmination of many years of mycological interests conceived from both personal and professional experiences dating back from my youthful hobbies of fungal observations and now, a humble aspiration to begin a mycological journey to usher Philippine fungal endophyte ecology forward into present literature. This endeavour begun as a budding mycological idea, and together with the encouraging and insightful contributions from Dr. Martin Unterseher and Dr. Thomas dela Cruz, this has developed into what has become a successful 3-year PhD research work. The years of work efforts included interesting scientific consultations with botanical experts
    [Show full text]
  • Rhe Weekly Arts and Entertainment Supplement to the Daily Nexus 2 a Thursday, December 7,1995 Daily Nexus
    rhe Weekly Arts and Entertainment Supplement to the Daily Nexus 2 A Thursday, December 7,1995 Daily Nexus Love For those of us who like KRS-ONE ture of What heard that Noel “Oasis” bubble gum and keeping 5. Album: Foo Fighters 11. Sunny Day Real Es­ Gallagher played on a fan- Bone Thugs 'N' Sattler our attention spans out of / Foo Fighters tate / LP2 tasmic, magical, mysteri­ firm commitments, I sub­ 6. Single (with two bo­ 12. Sonic Youth / Wash­ ous track, but in the end, mit a proposal for the top nus tracks): Edwyn Col­ ing Machine James learned a lot more five singles of the year. I lins / “A Girl Like You” 13. Built to Spill / There’s than he had planned to. / © #® ®\ thought this year was so 7. Album: GZA / Liq­ Nothing Wrong With Pete Shotton began to believe_ in reincarnation and it generally mediocre that a uid Swords Love 5. The Verve / A North­ made his eyes tear up. He dreamt about all the Mends he TLC song almost made 8. Video: Weezer / 14. Yo La Tengo / Electr- ern Soul had lost and all the places he had known. All the things this list. The stuff that was “Buddy Holly” O-Pura They may have broken he had tried to say seemed less important because of all good this year was great, 9. TV commercial: 15. Various Artists / Kids up in August, but the the unknown things he must have said. and everything else was Grand Puba, CL Smooth Original Motion Picture myths and shadows sur­ Reincarnation came just when he needed it He was 20 just a notch above that and Pete Rock for Sprite Soundtrack rounding the Verve con­ and lonely.
    [Show full text]
  • Tropical Plant List F
    Tropical Plant List F Pages loading too slowly! Click here to transfer to a less intensively visual version of this Online Catalogue for faster browsing! Homepage Online Catalog Plants in Limited Supply Garden Arts Gallery Fine Arts Gallery Site Map Show your discount. Plan for your Fall/Winter Click Here to Go to the next set of Plants in this alphabetical list of Tropical Plants! A selection of TROPICALS, some in very limited supply, covering the letter "F" This page contains the following plant groups: Fatshedera (Tree Ivy), Felicia (Vining Blue Daisy), Ficus (Fig Tree), Fittonia (Nerve Plant), Fortunella, Fosterella, Fuchsia. http://www.glasshouseworks.com/trop-f.html (1 of 22) [12/20/2009 9:50:04 PM] Tropical Plant List F You can use our new Shopping Cart by filling in the number of plants needed below and clicking on the "Order Now" button anywhere on our catalogue pages to the left of the plant entry. Our new Shopping Cart is the easiest way to order. After you have ordered your last selection, just follow the directions on the Shopping Cart page. You can order this way from any of our catalogue pages, wherever you see the "Order Now" button. If the Shopping Cart does not work, just click the "Fill In the Online Orderform" button above. 40501 FATSHEDERA LIZEI PIA ARAL HP PRICE: $4.75 "Curly Tree Ivy" Also often called "Botanical Wonder: for it is a hybrid of Aralia and Hedera. Star-shaped leaves deeply fluted (sometimes listed as F. undulata) on erect semi-woody stems. Tolerates considerable chill.
    [Show full text]