Preventive Maintenance Strategy for Train Doors Based on The
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Uk Debates: How Do We Build More Light Rail?
THE INTERNATIONAL LIGHT RAIL MAGAZINE www.lrta.org www.tautonline.com SEPTEMBER 2016 NO. 945 UK DEBATES: HOW DO WE BUILD MORE LIGHT RAIL? NET Phase Two economic impacts quantied Montpellier opens city tramway ring CRRC’s home-grown o-wire tram New York appoints Streetcar ‘czar’ ISSN 1460-8324 £4.25 09 San José Besancon5 America’s low-oor A simple, quality light rail convert system on a budget 9 771460 832043 LRT MONITOR e LRT MONITOR series from Mainspring is an essential reference work for anyone who operates in the world’s light and urban rail sectors. Featuring regular updates in both digital and print form, the LRT Monitor includes an overview of every established line and network as well as details of planned schemes and those under construction. POLAND POZNAŃ Tramways play an important role in one of of the main railway station. Poland’s biggest and most historic cities, with In 2012 a line opened to the east of the city, the first horse-drawn tramline opening in 1880. with an underground section containing two An overview Electrification followed in 1898. sub-surface stations and a new depot. The The network was badly damaged during World reconstruction of Kaponiera roundabout, an A high-quality War Two, resuming operations in 1947 and then important tram junction, is set for completion in of the system’s only east of the river Warta. Service returned to 2016. When finished, it will be a three-level image for ease the western side of the city in 1952 with the junction, with a PST interchange on the lower development, opening of the Marchlewski bridge (now named level. -

INTERIM REPORT 2018 BII RAILWAY TRANSPORTATION TECHNOLOGY HOLDINGS COMPANY LIMITED Corporate Information (Continued)
CONTENTS 2-3 Corporate Information 4 Consolidated Statement of Profit or Loss – Unaudited 5 Consolidated Statement of Profit or Loss and Other Comprehensive Income – Unaudited 6-7 Consolidated Statement of Financial Position – Unaudited 8-10 Consolidated Statement of Changes in Equity – Unaudited 11-12 Condensed Consolidated Cash Flow Statement – Unaudited 13-65 Notes to the Unaudited Interim Financial Report 66-67 Independent Review Report 68-77 Management Discussion and Analysis 78-86 Other Information Corporate Information BOARD OF DIRECTORS COMPANY SECRETARY Executive Directors Ms. Cheung Yuet Fan Mr. Cao Wei (Vice Chairman) Ms. Xuan Jing (Chief Executive Officer) AUDIT COMMITTEE Non-Executive Directors Mr. Luo Zhenbang (CPA) (Chairman) Mr. Guan Jifa (Chairman) Mr. Bai Jinrong Mr. Hao Weiya Mr. Huang Lixin Mr. Ren Yuhang Mr. Zheng Yi REMUNERATION Independent Non-Executive Directors COMMITTEE Mr. Bai Jinrong Mr. Bai Jinrong (Chairman) Mr. Luo Zhenbang (CPA) Mr. Cao Wei Mr. Huang Lixin Mr. Huang Lixin AUTHORISED NOMINATION COMMITTEE REPRESENTATIVES Mr. Guan Jifa (Chairman) PURSUANT TO RULE 3.05 Mr. Bai Jinrong OF THE LISTING RULES Mr. Huang Lixin Ms. Xuan Jing Ms. Cheung Yuet Fan AUDITORS KPMG Certified Public Accountants LEGAL ADVISERS TO THE COMPANY Chiu & Partners 2 INTERIM REPORT 2018 BII RAILWAY TRANSPORTATION TECHNOLOGY HOLDINGS COMPANY LIMITED Corporate Information (continued) PRINCIPAL BANKER BRANCH SHARE The Hongkong and Shanghai Banking REGISTRAR AND Corporation Limited TRANSFER OFFICE Tricor Investor Services Limited Level 22, Hopewell Centre REGISTERED OFFICE 183 Queen’s Road East Cricket Square Wanchai, Hong Kong Hutchins Drive P.O. Box 2681 Grand Cayman, KY1-1111 WEBSITE Cayman Islands www.biitt.cn HEAD OFFICE AND STOCK CODE PRINCIPAL PLACE 1522 OF BUSINESS IN HONG KONG Unit 4407, 44/F, COSCO Tower 183 Queen’s Road Central Sheung Wan, Hong Kong PRINCIPAL SHARE REGISTRAR AND TRANSFER OFFICE SMP Partners (Cayman) Limited Royal Bank House – 3rd Floor 24 Shedden Road P.O. -

Evolution of Urban Rail Signaling System Technology in China
Evolution of Urban Rail Signaling System Technology in China Mr. Dongjie Li Traffic Control Technology Co., Ltd. July-2019 Overview of China Rail 01 Transit Development CONTENTS Evolution of Signaling 02 System Technology of TCT « Overview of China Rail 01 Transit Development Overview of China Rail Transit Development 1969 2018 2020 We are experiencing a rapid development stage The first rail 132 urban rail 6000km transit line in lines China Beijing Subway Line 1 83% adopt By 2020, the total « built in July, 1965 and CBTC system, with operation mileage opened in January, operation mileage will be up to 6000km. 1971, with 10.7km. 4354.30km « Evolution of Signaling 02 System Technology of TCT Evolution of Signaling System product of TCT 2019 Intelligent rail transportation system 40 years R&D of signaling system 2018 Interoperable Fully automatic operation system Cloud Platform for urban rail systems 2017 Train Intelligent Detection System Rail transit 2016 Vehicle-vehicle communication based Train Trans-disciplinary control system Multi-field LTE based DCS system LCF-500 2015 Interoperable signalling system for network LCF-400 2014 Fully automatic operation 2011 Train operation centred Integrated automation Signaling System 2009 Information security LCF-300 2008 STM CBTC Pilot plant test LCF-200 2002-09 LCF-100 Beijing BaTong Line 1 LCF-200 Passenger dedicated Railway LCF-100 2004 CBTC R&D Subject communication device 1998 LCF-100 through appraisal Product 1996 Urban rail R&D ATP 1993 SJ-93 communication device Railway test 1990"Eighth -

Trams Der Welt / Trams of the World 2021 Daten / Data © 2021 Peter Sohns Seite / Page 1
www.blickpunktstrab.net – Trams der Welt / Trams of the World 2021 Daten / Data © 2021 Peter Sohns Seite / Page 1 Algeria ... Alger (Algier) ... Metro ... 1435 mm Algeria ... Alger (Algier) ... Tram (Electric) ... 1435 mm Algeria ... Constantine ... Tram (Electric) ... 1435 mm Algeria ... Oran ... Tram (Electric) ... 1435 mm Algeria ... Ouragla ... Tram (Electric) ... 1435 mm Algeria ... Sétif ... Tram (Electric) ... 1435 mm Algeria ... Sidi Bel Abbès ... Tram (Electric) ... 1435 mm Argentina ... Buenos Aires, DF ... Metro ... 1435 mm Argentina ... Buenos Aires, DF - Caballito ... Heritage-Tram (Electric) ... 1435 mm Argentina ... Buenos Aires, DF - Lacroze (General Urquiza) ... Interurban (Electric) ... 1435 mm Argentina ... Buenos Aires, DF - Premetro E ... Tram (Electric) ... 1435 mm Argentina ... Buenos Aires, DF - Tren de la Costa ... Tram (Electric) ... 1435 mm Argentina ... Córdoba, Córdoba ... Trolleybus Argentina ... Mar del Plata, BA ... Heritage-Tram (Electric) ... 900 mm Argentina ... Mendoza, Mendoza ... Tram (Electric) ... 1435 mm Argentina ... Mendoza, Mendoza ... Trolleybus Argentina ... Rosario, Santa Fé ... Heritage-Tram (Electric) ... 1435 mm Argentina ... Rosario, Santa Fé ... Trolleybus Argentina ... Valle Hermoso, Córdoba ... Tram-Museum (Electric) ... 600 mm Armenia ... Yerevan ... Metro ... 1524 mm Armenia ... Yerevan ... Trolleybus Australia ... Adelaide, SA - Glenelg ... Tram (Electric) ... 1435 mm Australia ... Ballarat, VIC ... Heritage-Tram (Electric) ... 1435 mm Australia ... Bendigo, VIC ... Heritage-Tram -

Trams Der Welt / Trams of the World 2020 Daten / Data © 2020 Peter Sohns Seite/Page 1 Algeria
www.blickpunktstrab.net – Trams der Welt / Trams of the World 2020 Daten / Data © 2020 Peter Sohns Seite/Page 1 Algeria … Alger (Algier) … Metro … 1435 mm Algeria … Alger (Algier) … Tram (Electric) … 1435 mm Algeria … Constantine … Tram (Electric) … 1435 mm Algeria … Oran … Tram (Electric) … 1435 mm Algeria … Ouragla … Tram (Electric) … 1435 mm Algeria … Sétif … Tram (Electric) … 1435 mm Algeria … Sidi Bel Abbès … Tram (Electric) … 1435 mm Argentina … Buenos Aires, DF … Metro … 1435 mm Argentina … Buenos Aires, DF - Caballito … Heritage-Tram (Electric) … 1435 mm Argentina … Buenos Aires, DF - Lacroze (General Urquiza) … Interurban (Electric) … 1435 mm Argentina … Buenos Aires, DF - Premetro E … Tram (Electric) … 1435 mm Argentina … Buenos Aires, DF - Tren de la Costa … Tram (Electric) … 1435 mm Argentina … Córdoba, Córdoba … Trolleybus … Argentina … Mar del Plata, BA … Heritage-Tram (Electric) … 900 mm Argentina … Mendoza, Mendoza … Tram (Electric) … 1435 mm Argentina … Mendoza, Mendoza … Trolleybus … Argentina … Rosario, Santa Fé … Heritage-Tram (Electric) … 1435 mm Argentina … Rosario, Santa Fé … Trolleybus … Argentina … Valle Hermoso, Córdoba … Tram-Museum (Electric) … 600 mm Armenia … Yerevan … Metro … 1524 mm Armenia … Yerevan … Trolleybus … Australia … Adelaide, SA - Glenelg … Tram (Electric) … 1435 mm Australia … Ballarat, VIC … Heritage-Tram (Electric) … 1435 mm Australia … Bendigo, VIC … Heritage-Tram (Electric) … 1435 mm www.blickpunktstrab.net – Trams der Welt / Trams of the World 2020 Daten / Data © 2020 Peter Sohns Seite/Page -

China Construction Civil Infrastructure Corp. Ltd
Credit Rating Report: China Construction Civil Infrastructure Corp. Ltd Issuer Credit Rating *: Aspc+; Outlook: Stable January 25, 2021 Analysts: Wang Kexin 010-65166033; [email protected] Zhang Renyuan 010-65166028; [email protected] Wang Huang 010-65166029; [email protected] Ren Yingxue 010-65166037; [email protected] Table of Contents Tear Sheet ................................................................................ 2 Rating Summary ...................................................................... 3 Credit Highlights ...................................................................... 3 Outlook ..................................................................................... 3 Assumptions and Forecasts ..................................................... 4 Adjusted Financials and Ratios................................................ 5 Economic and Industry Trends ................................................. 5 Company Description ............................................................... 7 Business Risk Profile ............................................................... 9 Financial Risk Profile ............................................................. 11 Peer Comparison .................................................................... 14 Liquidity ................................................................................. 16 Rating Score Snapshot .......................................................... 19 Related Methodologies and -

Use Style: Paper Title
2019 International Conference on Energy, Environmental and Civil Engineering (EECE 2019) ISBN: 978-1-60595-645-9 China Research Status of Ground Landscape Design for Subway Entrances and Exits Xiao-hui WU and Feng-jun LIU School of Architecture, Henan University of Science and Technology, Luoyang, Henan 471023, China Keywords: Subway entrance and exit, Landscape design, Literature review. Abstract. Main domestic documents about subway entrance landscape design has been analyzed. It has been concluded that subway entrance landscape concept, interaction of subway entrance and surrounding landscape, common features and individual features of subway entrance landscape, elements of subway entrance landscape, design strategies and design principles of subway entrance landscape, the optimization strategy for subway entrance landscape, subway entrance landscape element comment system establishing. And the research direction in the future has been raised. Introduction The subway system in China was first built in the capital Beijing. Beijing Metro Line 1 began its trial operation in January 1971. Since then, the construction of the subway in mainland has been developed slowly in about 30 years. Since the 21st century, the number of subways in China has grown exponentially, and people have begun to pay more attention to the design of ground landscapes of subway entrance and exit. The subway entrance and exit bear the heavy responsibility of people leaving the station, entering the station, and transferring the station, and are the link between the subway and the city [1]. The careful design of the ground landscape of the subway entrance and exit is not only the needs of functions, but also a combination of various needs such as urban construction, humanization and aesthetics in the new era. -
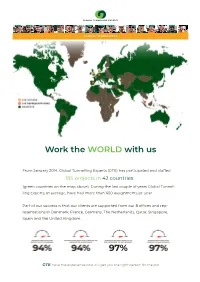
Work the WORLD with Us
Work the WORLD with us From January 2014, Global Tunnelling Experts (GTE) has participated and staffed 185 projects in 42 countries (green countries on the map above). During the last couple of years Global Tunnel- ling Experts, in average, have had more than 600 assignments pr. year. Part of our success is that our clients are supported from our 8 offices and rep- resentations in Denmark, France, Germany, The Netherlands, Qatar, Singapore, Spain and the United Kingdom. GTE have the experience and will get you the right person for the job DETAILED REFERENCELIST ALGERIA CANADA Yuncheng – Shanxi Dashuiwang Water Constantine – Beni Haroun PK 9 Kemano – Hydro Power T2 Completion Tunnel Diversion Project Saskatoon – Jansen Mine Xiamen – Metro Line 2 Phase 1 ARGENTINA Toronto – Coxwell Bypass Buenos Aires – Aguas del Parana Toronto – Crosstown COLOMBIA Buenos Aires – Riachuelo Margen Izquierdo Lot 1 Vancouver – Evergreen Line Bogota – Interceptor Tunjuelo Canoas Buenos Aires – Riachuelo Margen Izquierdo Lot 3 Vancouver – Water Supply Tunnel Outfall CZECH REPUBLIC Buenos Aires – Sarmiento CHILE Pilsen – Ejpovice Tunnelcomplex Buenos Aires – Tunel Aliviador Vega El Teniente – Mine El Teniente Las Lajas – Alto Maipo HEPP DENMARK AUSTRALIA Los Condores – Mine Los Condores Copenhagen – Damhusledningen Brisbane – Northern Link Santiago – Alto Maipo HEPP Copenhagen – Metro Line M4 Sydhavn Gold Coast – Marine Parade Volcano – Alto Maipo HEPP Extension Newcastle – Hunter Valley Water Melbourne – Spencer St Sewer Upgrade project CHINA ECUADOR Melbourne -

RFS Supports the Ramp-Up of Next-Generation Broadcast Networks
NewsNews from from RFS RFS IBC, RAI Amsterdam, Hall 8, Booth B34 10-March,14 September 6th, 2017 20 10 RFS DAS Solutions Enable Worldwide Network Deployments in Challenging In-Tunnel and In-Building Environments During 2016 End-to-end Solutions Including Cables, Connectors, Jumpers, Antennas and Passive Components Deliver Cost-Effective Coverage and Capacity for Commercial and Mission Critical Wireless Communications Networks Nozay (France), March 6th, 2017 — Radio Frequency Systems (RFS), the global wireless and broadcast infrastructure specialist, announced that it continues to experience worldwide growth in tunnel and in-building deployments in 2016. The company’s market-leading passive and active wireless networking solutions, including RADIAFLEX®, RFS’ patented radiating cables, were used by major mobile operators and integrators to deliver uninterrupted coverage and capacity in some of the most challenging indoor venues, metro rail tunnels, road tunnels, airports, and stadiums. RFS achieved deployments all over the world in 2016, including: Armenia: Multi-band 4G network for commercial radio in the Yerevan Metro Belgium: Brussels road tunnels Brazil: Multiple high-profile locations including strategic venues for Rio 2016 Olympic Games such as the Main Olympic Stadium (Engenhão Stadium), International Broadcasting Center (IBC), Main Press Center (MPC), Rio Centro venue and projects for more capacity at the Maracanã and Mineirão Stadiums; Several new hotels and malls in Latin America; Mission critical radio network (TETRA) for Metro Rio de Janeiro. China: Various RADIAFLEX® radiating cable based coverage solutions thereof Wuhan metro, Qingdao metro, Chengdu metro, Guangzhou metro and Nanning metro (multiple lines) o Hong Kong: Network replacement at ten selected stations and the associated running tracks on Island Line (ISL), Kwun Tong Line (KTL), Tsuen Wan Line (TWL), Tseung Kwan O Line (TKL) and West Rail Line (WRL) to support the additional mobile phone services of LTE signals in the frequency bands of 1800MHz, 2100MHz, 2300MHz and 2600MHz. -

China Fangda Group Co., Ltd
Annual Report 2020 of China Fangda Group Co., Ltd. China Fangda Group Co., Ltd. 2020 Annual Report March 2021 1 Annual Report 2020 of China Fangda Group Co., Ltd. Chapter 1 Important Statement, Table of Contents and Definitions The members of the Board and the Company guarantee that the announcement is free from any false information, misleading statement or material omission and are jointly and severally liable for the information’s truthfulness, accuracy and integrity. Mr. Xiong Jianming, the Chairman of Board, Mr. Lin Kebin, the Chief Financial Officer, and Mr. Wu Bohua, the manager of accounting department declare: the Financial Report carried in this report is authentic and completed. All the Directors have attended the meeting of the board meeting at which this report was examined. Forward-looking statements involved in this report including future plans do not make any material promise to investors. Investors should pay attention to investment risks. The Company needs to comply with disclosure requirements of the Shenzhen Stock Exchange Industry Information Disclosure Guideline No.6 – Listed Companies Engaged in Decoration Business and disclosure requirements of the Shenzhen Stock Exchange Industry Information Disclosure Guideline No.3 – Listed Companies Engaged in Property Development. The Company has specified market, management and production and operation risks in this report. Please review the potential risks and measures 2 Annual Report 2020 of China Fangda Group Co., Ltd. mentioned in the discussion and analysis of future development in IV. Operation Discussion and Analysis. The Company will distribute no cash dividends or bonus shares and has no reserve capitalization plan. 3 Annual Report 2020 of China Fangda Group Co., Ltd. -
Information for Prospective Candidates
INFORMATION FOR PROSPECTIVE CANDIDATES Thank you for your interest in Harrow Nanning. We hope you find the following information helpful and look forward to receiving your application Contents 1. Asia International School Limited 2. Harrow Innovation Leadership Academy Nanning 3. Message from the Head 4. Harrow International Schools • Leadership for a better World • Academic Progression • Boarding 5. Leadership values 6. The benefits of working with Harrow Family in Asia 7. Other Schools in The Harrow Asia Family • Harrow Bangkok • Harrow Beijing • Harrow Hong Kong • Harrow Shanghai 8. What we are looking for 9. Living and working in Nanning • Cost of Living • The transport system • Weather • Living in Nanning • Tourism • Hospitals and clinics • Shopping • Forums and Directories • Frequently Asked Questions ASIA INTERNATIONAL SCHOOL LIMITED The Leading Provider of World Class British international Education Building on Harrow School’s 450-year legacy of educational excellence, Asia International School Limited (AISL) has over 20 years of experience, operating Harrow international schools in Bangkok (1998), Beijing (2005), Hong Kong (2012) and Shanghai (2016). AISL is the holding company of Harrow International Schools (HISs), Harrow Innovation Leadership Academies (HILAs) and Harrow Little Lions Childhood Development Centres (HLLs). From 2020, HILAs will commence operations in several tier-one and tier-two cities in China, providing an outstanding K-12 bilingual and holistic education to local students, assuring a successful pathway to the world’s top universities. We currently operate two HLLs, in Shanghai, adjacent to our HIS, and in Chongqing. There are advanced plans to open several more in the near future. Harrow – 450 Years of Heritage Harrow School was founded in London in 1572 under a Royal Charter granted by Elizabeth I. -
Registration Form
REGISTRATION FORM REGISTRATION FEES CCES CHINA AND IEM MALAYSIA (0% GST EFFECTIVE JUNE 2018): JOINT SOUTHEAST ASIA SYMPOSIUM & EXHIBITIONS ON China Civil Engineering Society THE CHALLENGES AND STRATEGIC SOLUTIONS OF HIGH Grade Normal Fee Online Fee PROFILE PROJECTS ON TUNNELS 2018 (SEASET2018) (by fax & (Log-in TH TH CCES CHINA AND IEM MALAYSIA 18 – 19 SEPTEMBER 2018 email) IEMASB Email: [email protected] / [email protected] JOINT SOUTHEAST ASIA SYMPOSIUM & Website) Website: www.myiemasb.org.my EXHIBITIONS ON THE CHALLENGES AND IEM/CCES Mobile Membership Fees Member RM 950.00 RM 900.00 Name(s) STRATEGIC SOLUTIONS OF HIGH PROFILE No. No. / Grade (MYR) PROJECTS ON TUNNELS 2018 (SEASET2018) Non -IEM/CCES Member RM 1,400.00 RM 1,350.00 Organised by: China Civil Engineering Society (CCES) & The Institution of Engineers, Malaysia (IEM) PAYMENT METHOD AN EVENT ENDORSED BY: (a) Local cheque/Banker’s cheque made payable to “IEM ACADEMY SDN BHD ”. (b) Directly bank in or online transfer (Please forward soft copy of payment advice):- Total Amount Payable Managed by: IEM Academy (Including GST): (for inquiry please call +03-7931 5296 or visit www.iemasb.com) Account Name: IEM ACADEMY SDN BHD Account Number: 21403500139397 th th Company:_______________________________________ Event Date: 18 – 19 September 2018 Bank Name: RHB Bank Berhad Bank Address: No. 1, 3 & 5, Jln 52/18, PJ New ________________________________________________ Town Branch, 46050 Petaling Time: 8.00 am – 6.30 pm Jaya, Selangor, Malaysia Address:_________________________________________ 3 Coffee Breaks and 1 Buffet Lunch will Swift Code: RHBBMYKL be served in 5 -Star Hotel! ________________________________________________ Terms & Conditions Venue: Hilton Petaling Jaya, Kristal Ballroom 1, Level Mobile:_____________________Tel(O):_______________ V We wish to remind that all registration fees must be FULLY paid 1, West Wing, No.